金屬加筋壁板蒙皮有效寬度分析方法

宋子玲

(上海飛機設計研究院，上海 201210)

0 引言

航空器上的主要結構單元，如機身、機翼，是由蒙皮加筋結構組合(筋條可以是通過緊固件與蒙皮相連，也可以是整體機加形成)而成，這種蒙皮加筋結構通常被稱作壁板結構，典型的由“Z”型筋條與蒙皮組合的壁板結構如圖1所示。

目前，國內外對加筋壁板結構做了一系列的探索和研究，主要集中在有限元數值分析方法和工程理論計算結合試驗進行對比研究。

樊建超[1]提出了以體積等效來確定有蒙皮寬度的方法，介紹了自然網格建模時蒙皮有效寬度的含義及作用，列舉了一、二、三級凸臺蒙皮有效寬度的計算公式。雷一鳴[2]研究了機身壁板壓縮穩定性與蒙皮的有效寬度。認為承壓壓縮載荷的壁板結構蒙皮有效寬度均超過30倍蒙皮厚度，在工程分析中取30t(t為蒙皮厚度)是保守的；其次，加筋壁板結構的壓縮承載能力主要由筋條的壓損許用應力確定，對蒙皮厚度不明感。張國凡等[3]基于有限元與工程法相結合，利用蒙皮有效寬度剛度縮減的方法，采用線性迭代求解壁板結構的后屈曲問題，并表明采用該方法分析得到的破壞載荷與試驗結果更為接近。吳存利等[4]對薄皮鉚接Z型機身加筋壁板進行了研究，使蒙皮有效寬度計算誤差相較于試驗值控制在10%以內。雷一鳴[5]對大型客機鋁鋰合金機身壁板壓縮穩定性進行了試驗研究，驗證了傳統工程方法對鋁鋰合金壁板結構的偏差程度和適用性。提出了一種新的基于Johnson-Euler公式的修正算法，可以將計算結果與試驗值的偏差控制在5%左右。殷黎等[6]對隔框加筋結構壓縮許用載荷進行了分析，表明約翰遜—歐拉算法更適用于該結構類型的壓縮穩定性計算。劉存等[7]在提出加筋壁板彎曲承載能力等效法的基礎上，結合壁板軸壓試驗研究了三種蒙皮有效寬度計算方法的準確度,驗證了蒙皮長桁分離的計算方法吻合程度最高。

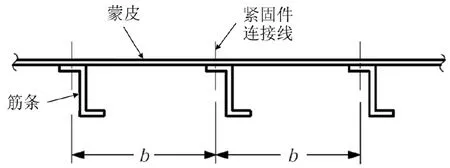
(a)典型壁板結構

本文通過結合工程方法及有限元分析，研究了民用飛機加筋壁板結構在承受軸向壓縮載荷下蒙皮有效寬度的計算方法，對工程應用具有重要的參考意義和價值。

1 蒙皮有效寬度的概念

板結構在承受面內一致的壓縮載荷時，當工作載荷小于蒙皮的屈曲失穩載荷時，壁板結構內部平行于加載邊的應力分布在蒙皮與筋條上一致，如圖2所示。

圖2 蒙皮未屈曲失穩時內部應力分布

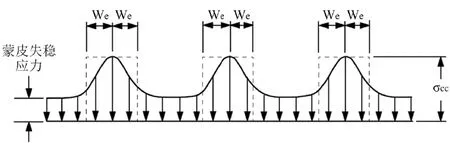
圖3 蒙皮屈曲失穩后內部應力分布

事實上，在有筋條加強的位置，蒙皮能夠承受更多的載荷；在超出筋條加強的位置，在一定范圍內，蒙皮依然能夠承受同筋條一樣多的載荷。如圖3所示，蒙皮應力分布通常較難用解析法表征，工程上，為了方便簡化計算，引入“蒙皮有效寬度”的概念來計算蒙皮的承載能力。

2 蒙皮有效寬度工程計算

2.1 Von Karman方法

在使用Von Karman方法計算蒙皮有效寬度時，首先要得到壁板結構單元的壓縮許用應力。壁板結構單元的壓縮許用應力按歐拉約翰遜公式計算，如公式(1)所示[8-10]。

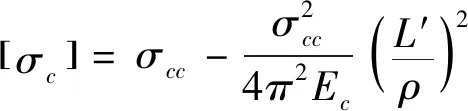
(1)

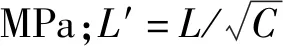
采用Von Karman方法計算的蒙皮有效寬度如公式(2)所示。

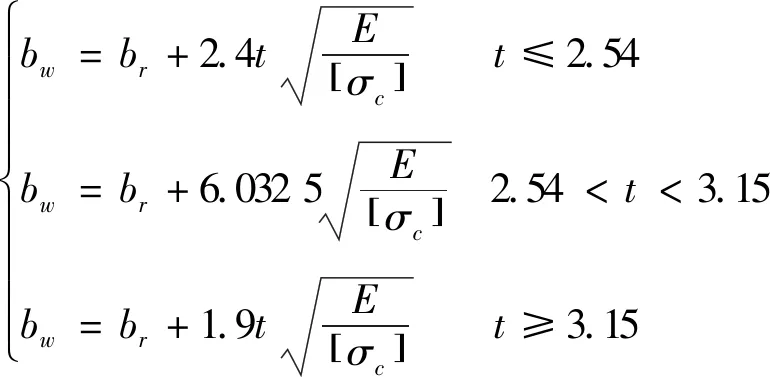
(2)

式中：bw為蒙皮有效寬度，mm；br為長桁間釘排距，mm；t為蒙皮厚度，mm；E為蒙皮壓縮彈性模量，MPa。

由于公式(1)、(2)中的[σc]是待求值，所以在求蒙皮有效寬度bw時可采用迭代法，具體步驟如下：

1)先求出筋條的壓損許用值σcc；

2)取迭代初始值[σc]=σcc；

3)按公式(2)計算bw；

4)根據得到的蒙皮有效寬度bw計算筋條、蒙皮組合結構單元的面積A和慣性矩I；

5)計算L′/ρ；

6)按公式(1)計算[σc]。

將算得的[σc]重復步驟3)到6)運算，直到前一次的[σc]與后一次算的[σc]相等，此時迭代收斂，可以得到真實的蒙皮有效寬度。

蒙皮有效寬度的限制條件為bwbs時，直接取bw=bs。

壁板受壓面積為Acr=bwt+Ast，其中Ast為筋條截面積(包括凸臺面積)。

2.2 方法二

在圖1所示的一個典型壁板結構單元中，若蒙皮內的應力分布如圖3所示，可以通過等效一致的在蒙皮有效寬度2We內筋條上的應力來代替。蒙皮有效寬度2We可以通過公式(3)計算得到。

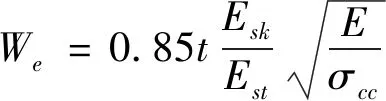
(3)

式中：We為以緊固件連接位置為中心一邊的蒙皮有效寬度，mm；t為蒙皮厚度，mm；Esk為蒙皮在應變(σcc/Est)下的割線模量，MPa；Est為長桁割線模量，MPa；E為蒙皮壓縮彈性模量，MPa；σcc為筋條壓縮許用應力，MPa。

當蒙皮與筋條的材料相同時，即Esk/Est=1，公式(3)中，蒙皮有效寬度由蒙皮的厚度、壓縮彈性模量及筋條的壓縮許用應力決定。筋條的壓縮許用應力取筋條穩定性、壓縮屈服應力、壓損應力值中的小值。

在有較大的抗扭剛度的筋條與薄蒙皮(比如b/t≥110)組合的壁板結構中，筋條對蒙皮的邊界支持作用大于簡支，有更多的蒙皮寬度可以用來承受壓縮載荷，可有效提高蒙皮有效寬度，公式(3)中的系數0.85可以提高到0.95。

結構設計時還需要綜合考慮使得筋條下的蒙皮在壓縮載荷下不發生釘間屈曲失效。為了有效規避該種失效模式，蒙皮有效寬度可以通過公式(4)進行修正。

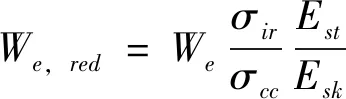
(4)

式中：We,red為縮減的以緊固件連接位置為中心一邊的蒙皮有效寬度，mm；σir為蒙皮釘間屈曲許用應力，MPa。

對于通過緊固件將筋條與蒙皮組合而成的壁板結構，常用的幾種構型及其蒙皮有效寬度、蒙皮有效面積如表1所示。

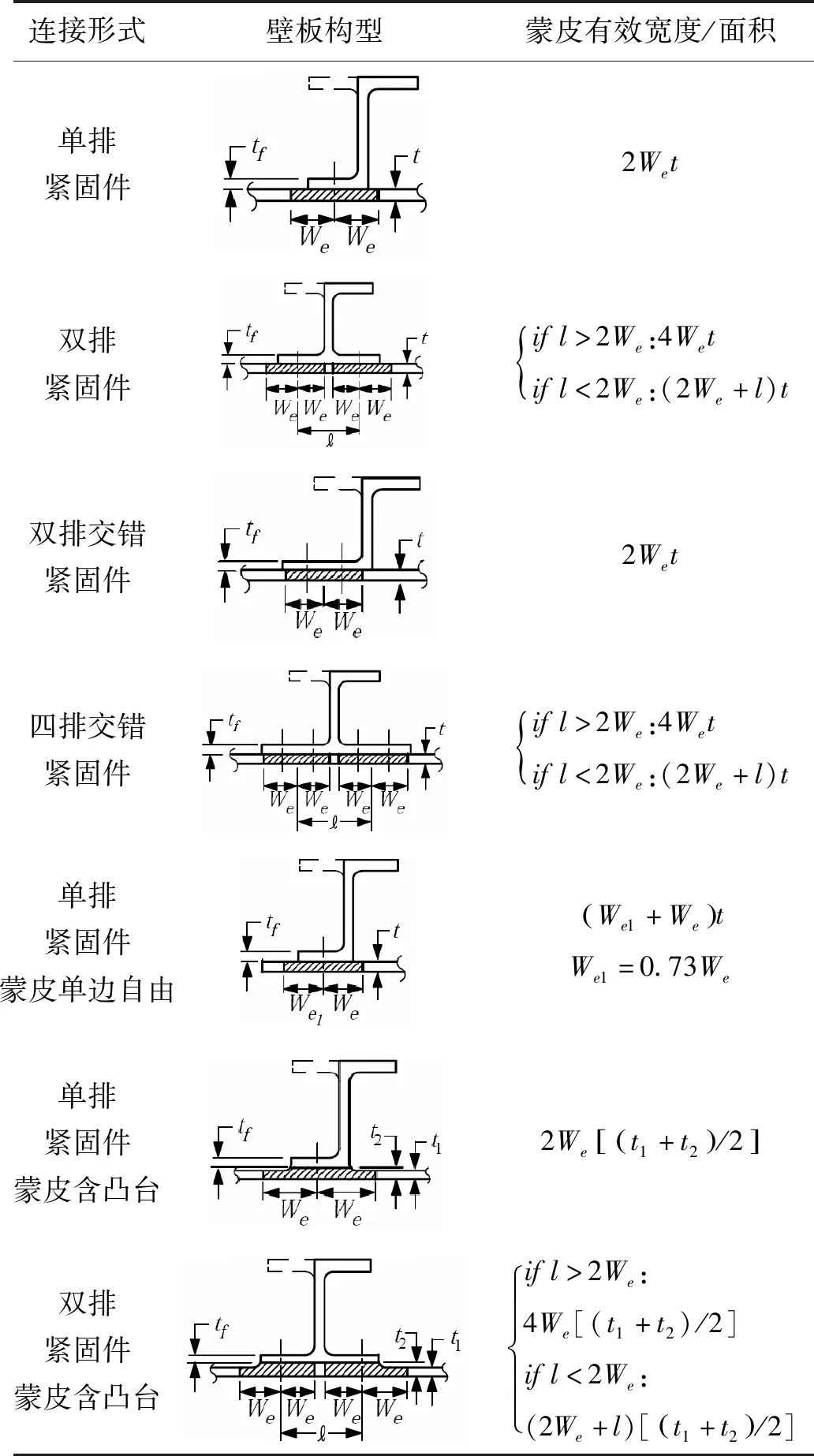
表1 通過緊固件組合的壁板結構的蒙皮有效寬度

對于通過整體機加的壁板結構，常用的幾種構型的蒙皮有效寬度、蒙皮有效面積如表2所示。

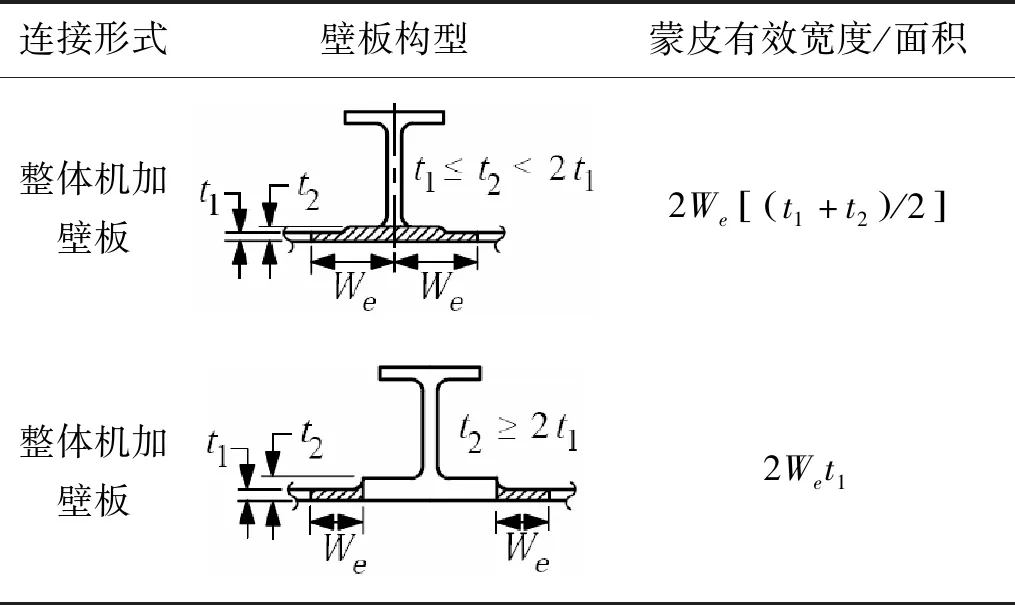
表2 整體機加壁板結構的蒙皮有效寬度

3 蒙皮有效寬度有限元分析

對于較復雜結構可以通過有限元分析來確定其蒙皮有效寬度。

下面通過一種典型壁板結構來分析有限元分析方法在確定蒙皮有效寬度中的應用。

典型壁板結構示意圖如圖4所示，長桁及蒙皮材料為7075-T6鋁合金，長桁通過兩排緊固件與蒙皮相連。

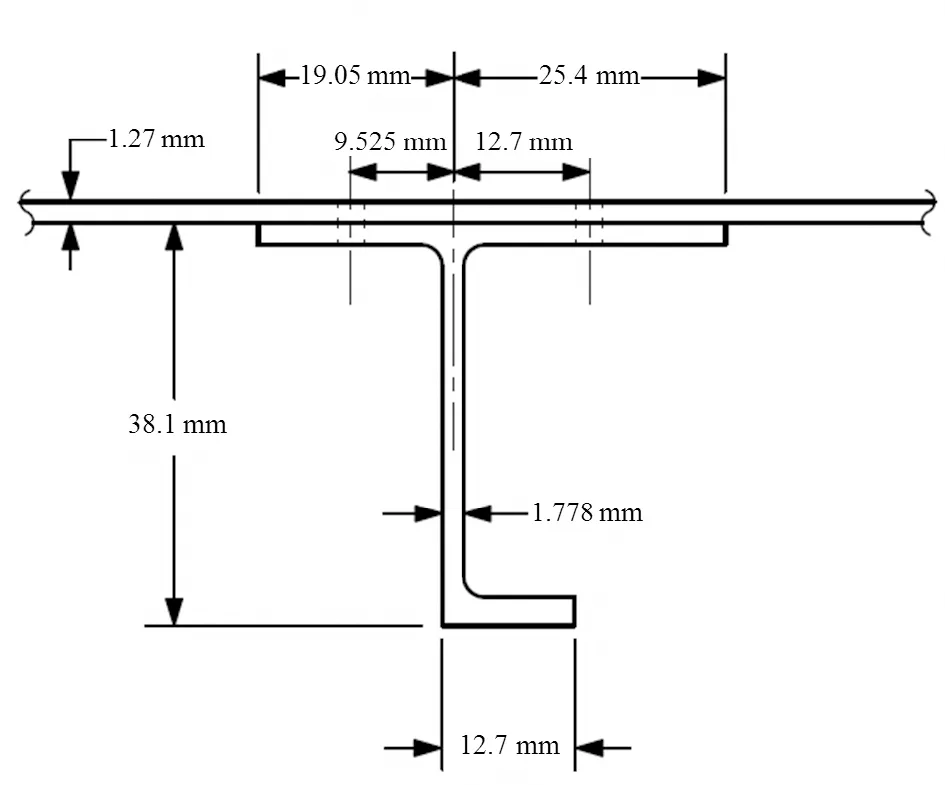
圖4 典型壁板結構示意

采用PATRAN建立的有限元模型如圖5～圖6所示。

(a)有限元模型視圖1

圖6 有限元模型邊界條件及加載

對建立的有限元模型采用NASTRAN 105求解器進行求解，得到其一階模態特征值，如圖7所示。可以看到，在壓縮載荷作用下，相鄰長桁間的蒙皮會首先發生屈曲失穩。

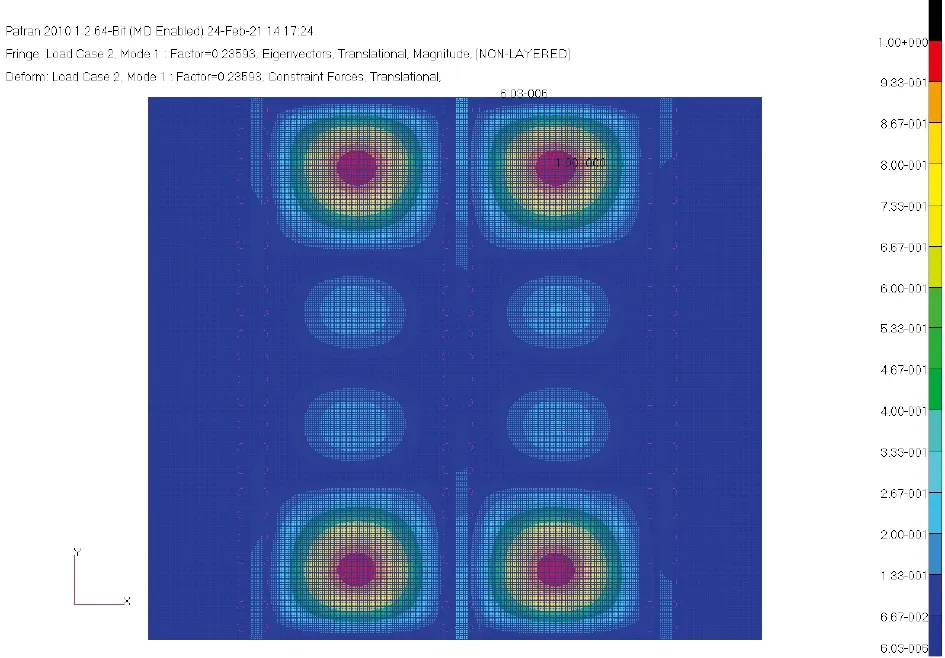
圖7 壁板結構一階模態(蒙皮失穩)

4 分析對比

表3給出了結合2.1、2.2章節的工程分析方法以及第3章節有限元分析計算的對比。結果顯示Von Karman分析方法與有限元計算方法結果較為接近，方法二分析結果較為保守。

表3 蒙皮有效寬度理論計算值與有限元計算值對比

在工程方法2的計算中，筋條有較大的抗扭剛度，b/t=200/1.27≥110，筋條對蒙皮的邊界支持作用大于簡支，有更多的蒙皮可以用來承受壓縮載荷，可有效提高蒙皮有效寬度，公式(3)中的系數0.85可以提高到0.95。

5 結論

1)采用Von Karman方法進行迭代計算得到的蒙皮有效寬度與有限元分析結果較為接近，能夠獲得較為準確的結果。

2)工程方法2中沒有考慮壁板結構的長度效應，其方法對較短的壁板結構分析時與工程方法1與有限元方法較為接近，具有一定的保守性。

3)Von Karman方法、工程方法2及有限元方法分析得到的蒙皮有效寬度均超過30倍蒙皮厚度，工程中常用的30倍蒙皮厚度的假設是保守的。