有限差分法的坐標變換誘導誤差

劉君，魏雁昕，韓芳

大連理工大學 航空航天學院，大連 116024

有限差分法應用于具有復雜外形的網格時需要進行坐標變換，即采用數學方法將流體力學控制方程由笛卡爾坐標系變換到與物體形狀相吻合的貼體坐標系(Body-Fitted Coordinates，BFC)以后再進行格式離散。在實際工程問題中，很少能直接給出坐標變換的解析表達式，因此，網格生成技術成為計算流體力學(Computational Fluid Dynamics，CFD)的一個重要分支。離散是對連續(xù)的近似表達，在生成的網格點基礎上計算坐標變換系數存在誤差。例如，一維函數u=u(x)從物理空間變換到計算空間ξ=ξ(x)，導數ux變成ux=ξxuξ，可以看出，如果坐標變換系數ξx采用數值算法得到，則必然也會引入誤差。算例表明，即使坐標變換系數ξx采用解析值，誤差依然存在，本文把這種由坐標變換引起的誤差稱為坐標變換誘導誤差。

早在1961年Trulio和Trigger[1]就注意到了這個問題，提出了一維問題中的“體積守恒(conservation of volume)”概念。1978年Steger等[2-4]研究了從守恒型控制方程出發(fā)計算具有復雜幾何外形的流場時坐標變換系數的影響，即使是均勻流場，采用傳統坐標變換系數求解方法也會產生非零源項，該源項由坐標變換引起，在流場中造成非物理解，嚴重時會引起數值振蕩，影響計算穩(wěn)定性[5-7]。1979年Thomas和Lombard[8-9]在前人研究基礎上提出了守恒型的坐標變換系數計算方法，并正式提出了被后來廣泛引用的幾何守恒律(Geometric Conservation Law，GCL)概念。根據計算過程中網格是否隨時間變形，GCL被進一步區(qū)分為“體積守恒律”(Volume Conservation Law，VCL)和“面積守恒律”(Surface Conservation Law，SCL)，前者解決“任意拉格朗日-歐拉”(Arbitrary Lagrange-Euler，ALE)方程動網格問題，應用范圍遠沒有后者普遍，目前在高精度格式領域研究GCL常指后者。本文后續(xù)提到的GCL也指“面積守恒律”。

按照文獻[9]中網格導數變換理論，如果使用二階精度格式離散uξ，那么采用中心差分格式離散ξx不影響導數ux的精度。基于上述認識，對GCL研究工作基本停頓下來，隨著高階精度格式的發(fā)展與應用這個問題又引起重視。從1999年Gaitonde和Visbal[10]提出了緊致格式的GCL以來，近20年來對基于高精度有限差分的GCL的研究得到了充分發(fā)展，其中2011年鄧小剛等證明了滿足GCL的充分條件[11]并提出了坐標變換系數的守恒計算方法——C MM(Conservative Metric Method)算法；隨后，在2013年進一步發(fā)展出了坐標變換系數計算結果唯一的對稱守恒計算方法——SC MM算法(Symmetrical Conservative Metric Method)[12]，該研究成果對于緊致類格式具有普適性指導意義。近年來科研工作者們對構建WENO格式的GCL時常借鑒其思想，如將WENO格式分解成中心差分部分及數值耗散部分[13-15]，中心部分直接采用SC MM計算。

文獻[15]的觀點“面積守恒律的簡化過程中，用到兩個數學前提，即網格物理坐標對計算坐標連續(xù)可導和混合導數都連續(xù)。但是在實際計算過程中，不能保證計算網格坐標點等間距或二階可導，簡化過程中所做假設不成立，并且網格導數由數值差分格式計算得到，因此引入數值誤差”在GCL研究領域具有普遍性。為了驗證上述結論，針對坐標變換函數的各階導數和混合導數均存在且連續(xù)的若干算例進行考查。

1 數值現象

目前常見的高精度格式大多包含隨著流場變化的模板或限制器，對于參數變化的流場難以區(qū)分誤差來源是差分格式還是幾何誘導。因此，選擇超聲速均勻流動，來流馬赫數M∞=2，無量綱流動參數(ρ,u,v,p)=(1.4,2,0,1)，其中ρ、u、v、p分別為無量綱密度、X方向速度、Y方向速度和壓力。從二維Euler方程出發(fā)進行數值模擬，首先給出柱坐標算例。

1.1 柱坐標均勻網格的坐標變換誘導誤差

由柱坐標和直角坐標之間的變換函數及其逆函數可以寫出解析表達式：

(1)

式中：r為圓環(huán)區(qū)域半徑；x為X軸方向坐標，x=rcosθ；y為Y軸方向坐標，y=rcosθ；θ為徑向網格線與X軸正向夾角。

計算區(qū)域為r∈[1,2]的圓環(huán)，沿徑向r和周向θ網格均勻分布，徑向網格點總數Nξ=51，周向網格點總數Nη=(360/7.2)+Nη0，其中Nη0為θ=0°網格線沿圓周方向編號。為便于處理周向邊界條件，進行計算域的拓展，例如，一階迎風格式沿周向拓展2個點，編碼η=Nη0=1和η=51 重合于x軸(即θ=0°網格線)，編碼η=0和η=50 對應θ=-7.2°的網格線，編碼η=2和η=52均是θ=7.2°的網格線，對于七點WENO格式需拓展更多的點，此時Nη0=3，但是網格夾角保持不變。

基于以上設定條件，計算空間坐標和柱坐標之間的線性關系為

(2)

計算中用到的5個坐標變換系數解析求出：

(3)

對流項計算采用一階迎風離散格式及Van Leer通量分裂格式，計算收斂以后數值解和理論值的誤差就是坐標變換誘導誤差，其流動參數誤差的分布規(guī)律類似，此處以密度誤差為例進行分析。當流場徑向內外圓邊界根據Riemann不變量處理時，其密度誤差δρ分布如圖1(a)所示，由于超聲速流動擾動不會向上游傳播，流場中x<0區(qū)域(左側半圓)的計算結果定性合理，但是在x>0 區(qū)域存在明顯的邊界影響。采用固定邊界值的方法處理徑向內外圓邊界也可以得到收斂解，其密度誤差分布云圖如圖1(b)所示，可以看出，流場參數誤差分布左右兩側不對稱特性依然存在。當徑向外圓邊界采用Riemann不變量處理時，內圓邊界把x<0出口值作為在y相等高度上x>0對應點的入口值，其計算結果如圖1(c)所示，可以看出流場參數誤差在x=0左右兩側呈現對稱分布。由此可以推斷：圖1(a)和圖1(b)中流場密度誤差分布出現左右兩側不對稱的原因是在x>0內環(huán)進口邊界處理中沒有考慮坐標變換引起的誤差。

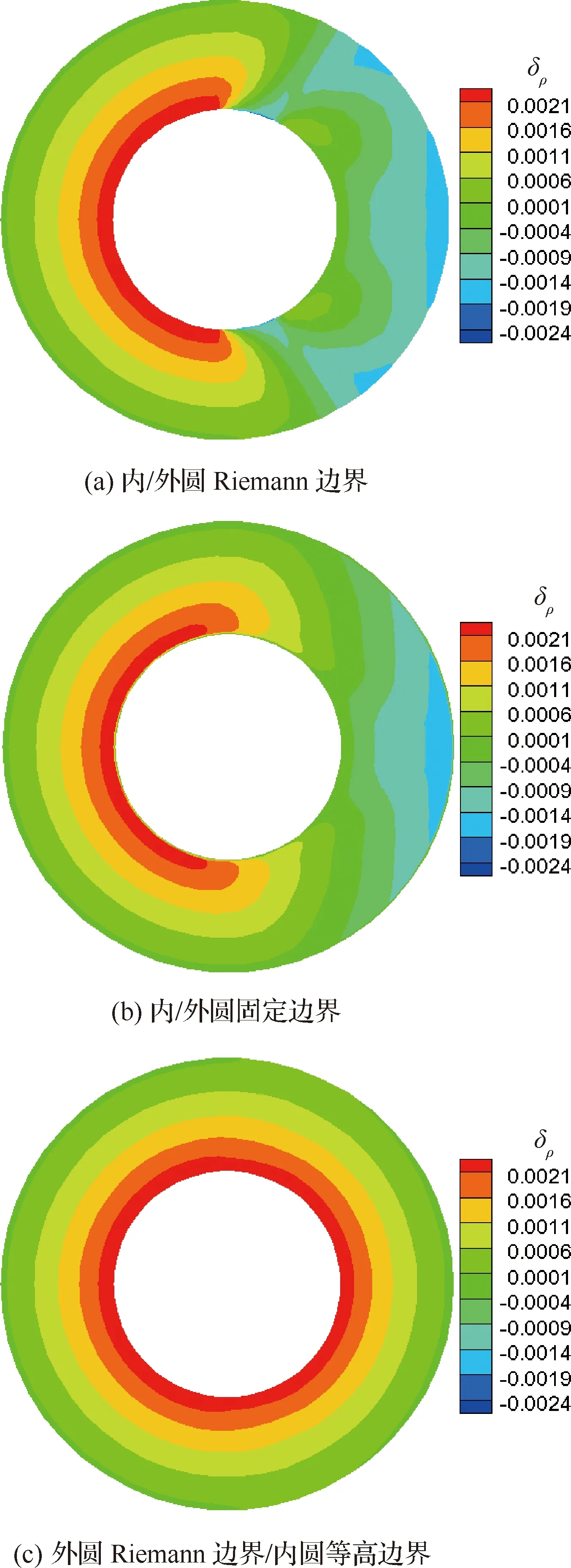
圖1 3種邊界條件下密度誤差云圖

定量比較圖1密度誤差特性，可以看出圓柱上游誤差分布相等且不受內圓邊界處理影響，因此，僅對x<0區(qū)域的密度誤差分布進行分析。為了后續(xù)研究，坐標變換系數除了采用式(3)求導的理論值，還采用二階中心格式的數值解進行計算，圖2為不同的系數計算方法和不同的差分格式下密度誤差δρ比較，為便于對比兩種格式，誤差云圖選取相同幅值。從結果看，WENO格式的誤差比一階迎風格式更大。

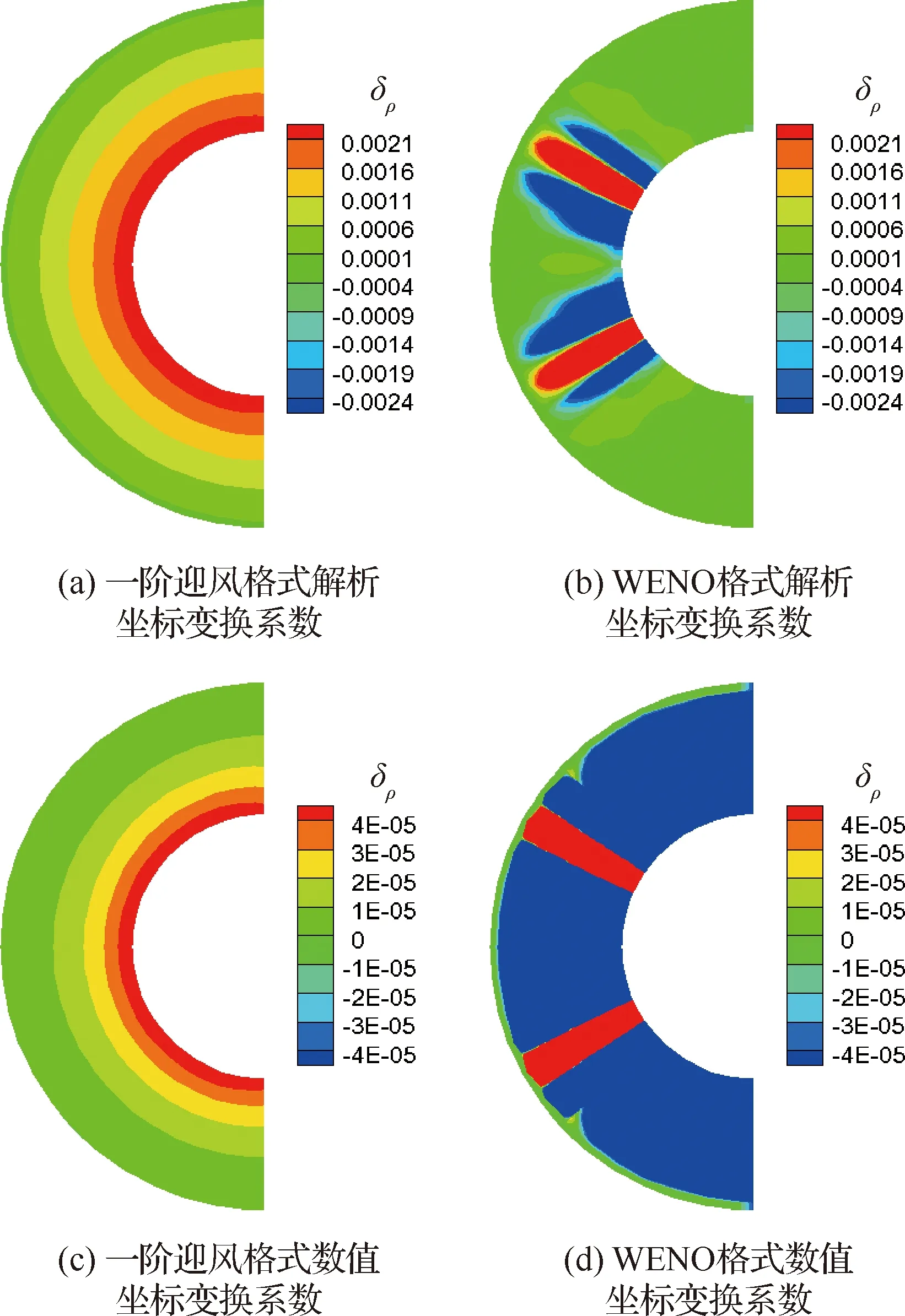
圖2 柱坐標系密度誤差云圖

同心圓網格算例表明進出口邊界變換成曲線以后，坐標變換也有影響，在超聲速流動穩(wěn)定性、氣動聲學、湍流轉捩等研究中，上游微小的擾動會導致結果出現差異，數值模擬過程中應該分辨和評估這種進口邊界誤差的不均勻特性對結果造成的干擾。為了排除進口邊界的影響，進行1.2節(jié)的數值實驗。

1.2 正弦函數網格的坐標變換誘導誤差

設計了如圖3(a)所示的拼接網格，左側第1塊網格(x≤0.6)完全是直角坐標系下的均勻網格：

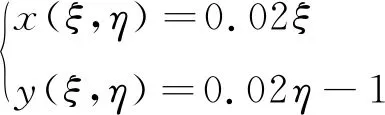
(4)

式中：0≤ξ≤30, 0≤η≤100。

第2塊網格(x>0.6)按照如式(5)所示的變換函數生成：

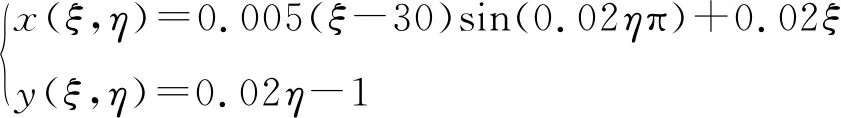
(5)

式中：31≤ξ≤130, 0≤η≤100。

計算中用到的坐標變換系數可以解析求出，5個系數中有2個為常數：

(6)

另外3個系數J、ξx、ξy的分布如圖3所示，JACB代表雅可比行列式，可以看出，在拼接線x=0.6處整體來說存在明顯不連續(xù)，但是在y=-1,0,1坐標處系數基本上光滑過渡。

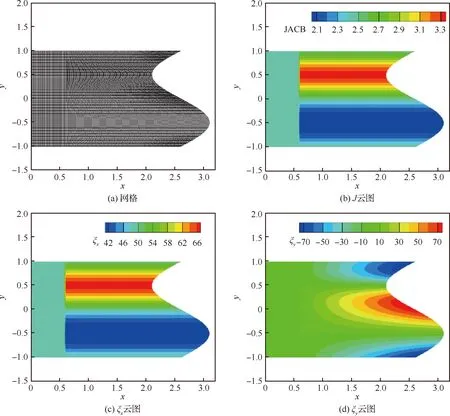
圖3 正弦網格及其變換系數

采用Steger通量分裂格式，不同離散格式和坐標系數計算方法得到的密度誤差特性如圖4所示，可以看出邊界處理對計算結果沒有影響。同樣WENO格式的計算誤差比一階迎風格式更大，其原因將在后文中討論，這里主要關注坐標系數精度的影響。

圖2和圖4的計算結果均表明坐標系數計算方法影響坐標變換誘導誤差，采用二階中心格式數值解的誤差比根據式(3)解析求得的誤差小兩個數量級。

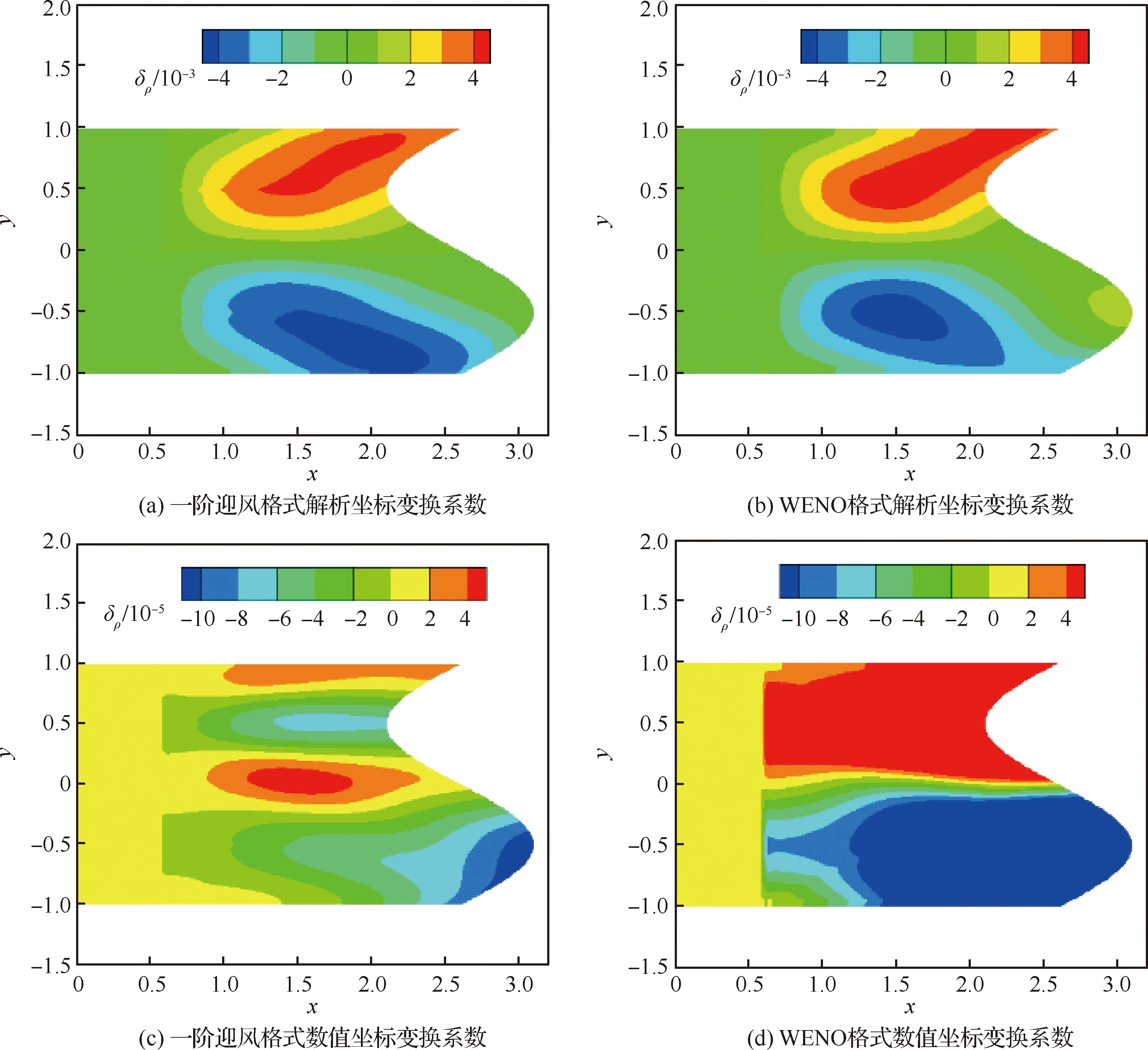
圖4 不同坐標變換系數下正弦網格密度誤差云圖

GCL研究的理論基礎如前所述，從Steger等研究GCL開始[2-4]，就是針對差分格式構建更高精度的坐標系數計算方法，從而實現不影響方程整體離散精度的目標，例如，按照滿足SC MM算法計算ξx，對于五階精度WCNS-E-5格式，需要六階中心插值[16]，同樣對于WENO格式ξx也是形式復雜的高精度插值[13-15]。原則上坐標系數計算方法的精度極限是準確的理論值，圖2和圖4 密度誤差云圖中數值解的誤差比解析解的還要大，這種現象與GCL的研究目標似乎相矛盾。

從同心圓算例和正弦網格算例計算結果可以看出，在“網格物理坐標對計算坐標連續(xù)可導和混合導數都連續(xù)”這兩個數學前提成立條件下，即使坐標系數采用理論值誤差依然存在，由此看來，認為坐標變換誘導誤差來自變換導數不連續(xù)的觀點不準確，不是坐標系數計算方法及其精度可以解決的問題。

目前建立的GCL算法針對不同的對流項離散格式，還沒有考慮通量分裂格式這個因素。圖5 是一階迎風格式條件下坐標變換系數解析求解采用AUSM、HLLC、ROE、Van Leer 4種通量分裂格式的壓力誤差δp云圖。采用WENO格式得到的誤差更大，分布類似，這里不再顯示。

從圖5中可以看出，不同通量分裂格式的坐標變換誘導誤差存在差異，研究GCL時應該考慮這個因素。GCL把坐標變換誘導誤差歸因于網格，但是調研未看到網格質量因素如何影響的定量研究文獻。網格生成技術研究領域經常采用正交性、光滑性和合理分布性評價網格質量[17]，前述柱坐標算例不但變換函數的導數連續(xù)，而且均勻網格完全正交且光滑，依然存在坐標變換誘導誤差，說明這些網格質量評價因素未能反映問題的本質，設計1.3節(jié)的算例對這個問題進行數值實驗。

圖5 不同通量分裂格式的壓力誤差

1.3 網格正交性和光滑性的影響

在柱坐標結果(圖1和圖2)分析中，注意到誤差分布具有軸對稱特征，考察計算中用到的5個坐標變換系數分布，只有雅可比行列式J是軸對稱的。在正弦函數網格中沿著y=-1,0,1這3條線點J變化較小，對應的誤差也較小。為考察J和坐標變換誘導誤差之間的關系，設計和計算了正交網格和非正交網格。對于網格線與坐標軸平行的完全正交網格，坐標系數ξy=ηx=0，所有算例中的J、ξx和ηy同時不為常數，圖6(a)和圖6(b)為指數加密網格及J云圖。可以看出存在明顯的不均勻特性。除了常用的指數加密，還計算了Δxi+1=αΔxi和Δyi+1=βΔyi等比例加密，其中Δxi和Δyi為i點處網格尺度，α和β為參數，計算網格如圖6(c)所示，計算中坐標變換系數采用二階中心差分的計算值，該網格下J云圖如圖6(d)所示。圖6(a)和圖6(c)兩種網格下的誤差云圖如圖7所示，說明單純J變化不一定產生坐標變換誘導誤差。由于相鄰網格之間的網格尺度Δx和Δy均不相等，從網格質量評價因素看光滑性不夠好，因此選取α=β=2.00得到的網格光滑性較差，且網格節(jié)點數減少為圖6(a)和圖6(c)中網格的1/10，該網格實際應用很少采用，計算結果也沒有發(fā)現誤差，至少表明對均勻流動來說，光滑性不會引起坐標變換誘導誤差。

將圖6(a)中的直角網格變成如圖8(a)所示的傾斜網格，在不光滑網格基礎上考查正交性的影響。網格線傾斜以后除ηx以外其余4個坐標系數均不為常數，定義網格y軸與x軸負向的夾角為θ′，例如θ′=45°工況下J、ξx和ξy分布如圖8(b)～圖8(d)所示。在0°<θ′<180°范圍內，選擇夾角參數θ′=m×15°(m=1,2,…,11)進行數值實驗，圖9給出了夾角參數θ′=30°、θ′=45°和θ′=120° 的計算結果，所有算例的誤差云圖和圖7相同，均沒有坐標變換誘導誤差，說明在光滑性較差的情況下，夾角保持常數時正交性較差的網格也不會產生誤差。

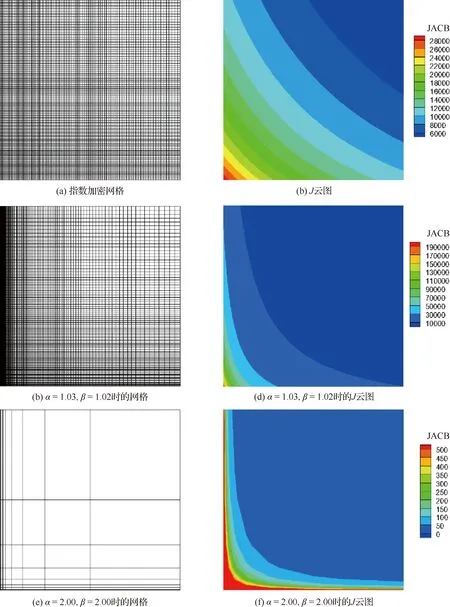
圖6 正交網格參數

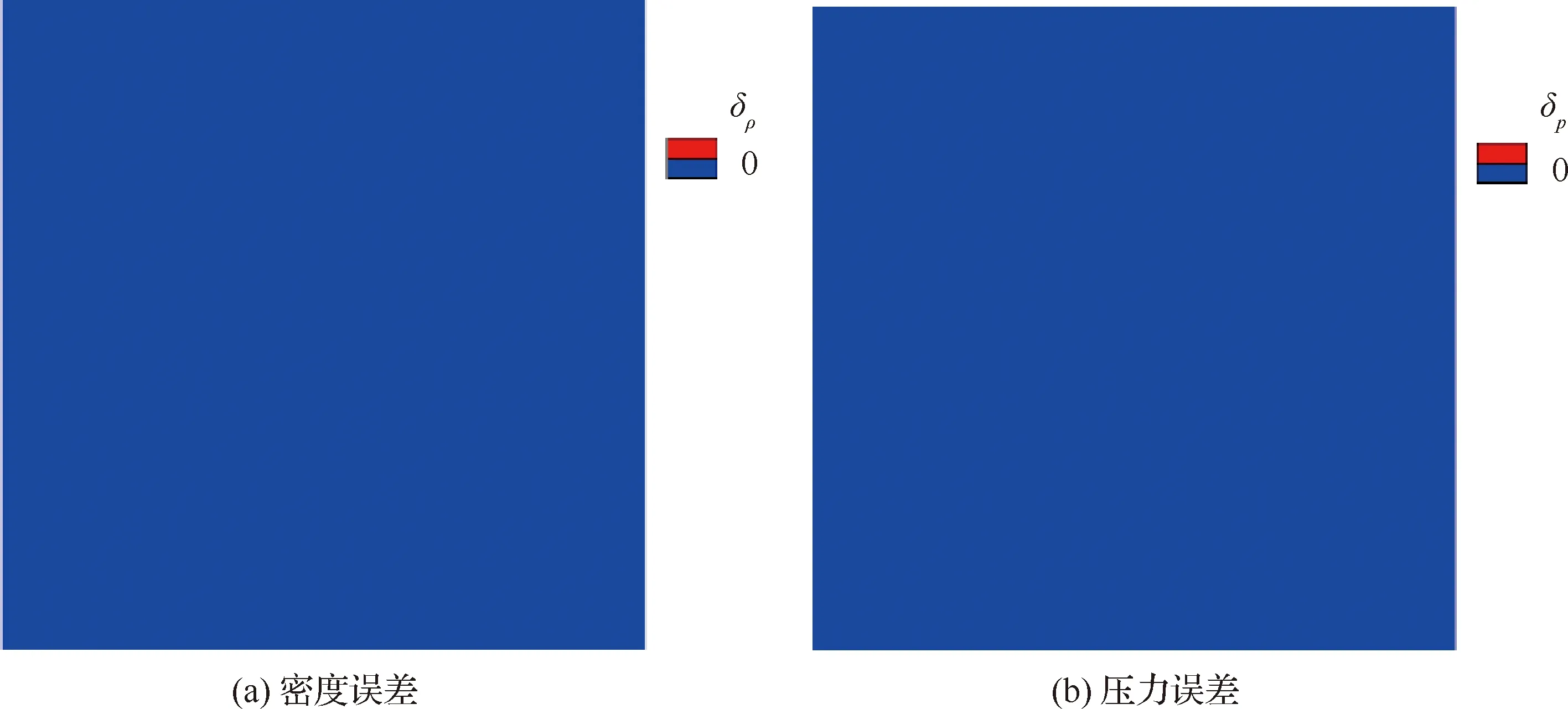
圖7 3種網格誤差云圖

圖8 45°夾角傾斜網格及其坐標系數分布

圖9 不同夾角傾斜網格密度誤差云圖

通過以上數值現象，可以得出：

1) 坐標變換誘導誤差來自“網格物理坐標對計算坐標的變換函數的導數不連續(xù)”的觀點不準確。

2) 不能僅采用網格的正交性和光滑性評估坐標變換誘導誤差的影響特性。

2 坐標變換誘導誤差的機理

將笛卡爾坐標系下(t,x,y,z)的三維守恒型Euler方程變換到貼體坐標系(τ,ξ,η,ζ)，其中t為時間，τ為貼體坐標系下的時間，ζ為三維空間貼體坐標下與ξ、η軸成右手系的坐標。其中得到原始形式：

UIt+FIx+GIy+HIz=S

(7)

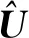
如果不考慮“體積守恒律”，那么It=0。“面積守恒律”方程為

(8)

式中：ξz、ηz、ζx、ζy和ζz均為坐標變換度量系數。以Ix=0為例，根據逆變換關系式得

(9)

式中：yζ、zξ、zη和zζ均為逆變換度量系數。繼續(xù)求導，以式(9)中第1項為例，得

y″η ξzζ+yηz″ζ ξ-z″η ξyζ-zηy″ζ ξ

(10)

式中：上標″表示求二階偏導數。

原則上在給定網格點(x,y,z)ijk位置以后，可以按照式(3)計算ξx，但是由于存在計算誤差，導致Ix=0不成立，即使對均勻來流也存在引起質量不守恒的現象，這就是產生坐標變換誘導誤差的機理。

根據式(10)可以看出，即使yη和ξx采用準確的理論值，由于還有?/?ξ的離散誤差，恒等式也是不成立的，依然存在坐標變換誘導誤差，可以合理解釋1.1節(jié)和1.2節(jié)算例采用理論值也出現坐標變換誘導誤差的數值現象。坐標變換系數采用數值解抹平了yη和ξx的變化斜率，對應的?/?ξ也較小，形成的源項S也較小，由此可以解釋圖2和圖4中出現的二階中心格式數值解的誘導誤差比準確的理論值還要小的數值現象。同樣，考查1.3節(jié)網格正交性和光滑性的算例，如果在離散以后恒等式還成立，那么也沒有誤差。

認識到坐標變換誘導誤差的機理和坐標變換系數的理論值無法消除誤差，那么就通過構建yη、ξx和?/?ξ相互匹配的算法使在離散空間上恒等式Ix=Iy=Iz=0重新成立，這就是GCL的出發(fā)點。由于yη和ξx只能計算得到，在GCL研究領域有個無法擺脫的邏輯困境：坐標變換系數采用解析值是不滿足GCL算法的。

3 幾何守恒律算法

從量綱角度分析，yη等參數對應矢量，ξx等參數是矢量面積，J-1對應體積，如果采用二階中心差商計算矢量，涉及離散點(x,y,z)ijk及其相鄰網格點正好形成六面體，在網格分布非等距情況下，采用不同算法得到的yη結果不同，網格點不共面情況下矢量面積ξx也與算法相關，得到的體積也不唯一，因此，早期CFD應用中Steger等解釋Ix≠0的原因就是矢量、面積和體積的算法不相容，采用一種加權平均算法計算坐標變換系數，解決了二階中心格式離散流動方程時遇到的問題[2-4]。后來研究者發(fā)現，如果流動方程的離散格式非二階中心格式，即使采用Steger等幾何相容滿足Ix=0等面積守恒律，依然存在均勻來流質量不守恒的現象，認識到計算式(10)中y″ηξ等二階混合導數與流動方程的離散格式相關，不同格式需要相適應GCL算法，其中鄧小剛等[12]提出的SC MM實際上是一個普適性的準則，應用該準則能夠滿足面積守恒律要求，即Ix=Iy=Iz=0。

按照SC MM準則，如果計算過程中流動方程算子發(fā)生變化，坐標變換系數的算子也要做相應調整。例如對于一階迎風格式，在時間迭代過程中流動算子隨著參數動態(tài)變化，滿足SC MM要求的坐標變換系數算子也要具有迎風特性，且每步需要重新計算，這給具體應用帶來困難。目前SC MM主要應用于格式模板系數確定的格式，從給出的均勻流動計算看，對于可以寫成若干中心格式組合的高階精度緊致類格式效果明顯，對于WENO格式不能完全消除坐標變換誘導誤差[14]，推測與其中的迎風型模板有關。

目前的GCL算法僅與格式相關，如果再將通量分裂格式、限制器等因素增加進來，沿著這條技術路線消除坐標變換誘導誤差構建的算法會非常復雜，預測將給應用帶來困難。

4 離散等價方程算法

除了第3節(jié)中所述GCL外，另一種思路是2018年劉君等提出離散等價方程算法[18]，放棄對恒等式Ix=Iy=Iz=0的約束條件，在離散對流項的同時也離散S≠0源項，以此消除坐標變換誘導誤差。下面對該算法進行簡單介紹。

坐標變換系數在以上三維守恒型Euler方程通量中是線性的，引入

(11)

對流項通量和源項表示為

(12)

(13)

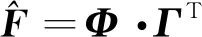
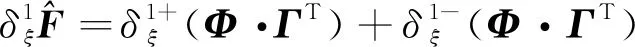
(14)

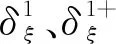
根據Steger和Van Leer通量分裂格式的通用表達式，可以直接證明坐標變換系數在通量分裂以后也是線性的，算子分別作用后

(15)

同樣使用算子δ1離散源項：

(16)

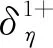
得到半離散形式：

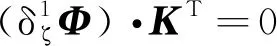
(17)

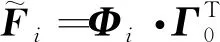
(18)

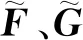
對于Steger和Van Leer通量分裂格式可以推導出如式(18)所示的離散方程的算子形式，由于AUSM、HLLC和Roe通量分裂格式是在半點處重構出來的，直接推導難度較大，采用數值實驗驗證，計算結果也沒有誤差。圖10和圖11是采用離散等價方程算法后第1節(jié)部分算例的計算結果，可以看出離散等價方程算法完全消除了坐標變換誘導誤差。

圖10 柱坐標系密度誤差云圖(一階迎風)

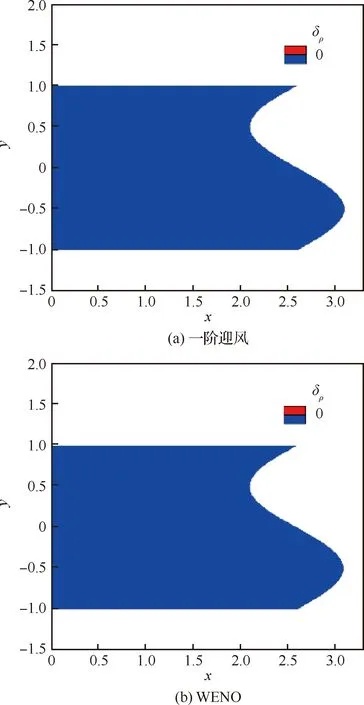
圖11 采用離散等價方程算法后的正弦網格密度誤差云圖

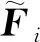
采用算子形式證明離散等價方程算法適用于任意格式，近期比較一階迎風格式和五階ENO類格式[20]，計算結果和1.1節(jié)、1.2節(jié)定性一致，高精度格式的坐標變換誘導誤差更大，通過分析誤差來源，得出的結論是ENO模板涉及的周圍相鄰網格點較多，在源項較大的局部區(qū)域引入的誤差較大，結論與本文一致。

式(11)～式(18)從帶有S≠0源項的離散等價方程算法推導中，算子作用在對流項守恒通量上，有些高精度格式采用原始變量重構界面的形式，討論這種基于原始變量的離散等價方程算法實現。

5 非均勻網格界面通量重構

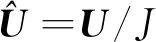
以密度為例進行討論，笛卡爾坐標系下均勻網格的MUSCL格式為

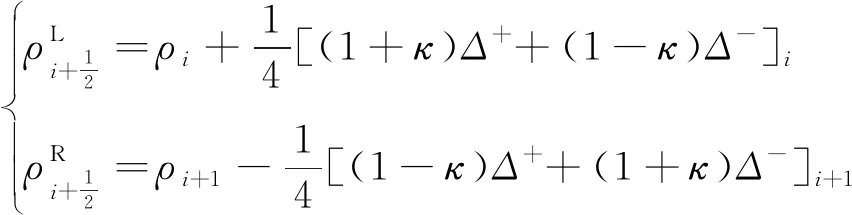
(19)

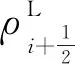
(20)

對應二階精度的3點中心格式：

(21)

根據Taylor級數：

(22)

(23)

式中：Δx1和Δx2分別為i點與i+1點網格間距和i點與i-1點網格間距；O(·)代表截斷誤差。

可以看出在非均勻網格Δx1≠Δx2條件下，應用MUSCL的3點中心格式式(21)達不到二階計算精度，在該種網格下二階精度格式表示為

(24)

分析計算空間內3點中心格式的精度：

(25)

不論坐標變換函數如何變化，其實質是物理空間到網格編碼的映射關系。以一維空間進行簡要說明，通過變換函數ξ=ξ(x)把物理空間x∈[a,b]映射到計算空間ξ∈[ξ(xa),ξ(xb)]，其中xa和xb分別為物理空間中a、b兩點坐標，把ξ空間離散成N個網格點，格點間距為常數：

Δξ=[ξ(xa)-ξ(xb)]/(N-1)

(26)

計算中網格編碼i和ξ之間存在線性關系i=1+[ξ(xi)-ξ(xb)]/Δξ，常數Δξ合并至坐標變換系數中，因此在離散后本質還是物理空間x∈[a,b]到i∈[1,N]的映射關系。實際應用中很少引入上述中間變換，而是直接從x∈[a,b]映射到ξ∈[1,N]，在計算空間離散點上滿足ξi=i。在離散后的計算空間上Δξ=1，決定計算空間大小的唯一參數是網格節(jié)點數N，如果網格加密過程中節(jié)點總數N保持不變，實際上只是調整離散點在物理空間[a,b]分布，與計算空間的映射關系沒有任何變化。如果通過增加網格總數N加密網格，即使物理區(qū)域[a,b]保持不變，其在計算空間的映射關系也發(fā)生相應的變化。

根據以上分析可知通過式(25)難以直接得到截斷誤差量級，嚴格的精度分析還需要變換至物理空間，由Taylor級數可得

(27)

由于Ji+1同樣需要Taylor展開，具體推導過程非常復雜，因此針對一維空間變換函數ξ=ξ(x)進行定性的量級分析。

根據微分關系式dξ=ξxdx可以得到坐標變換系數的量級ξx～O(Δx-1)，進一步推導出高階導數量級：

(28)

式中：f代表任意變量，用于任意物理量的高階導數量級分析。

在空間多維情況下，J至少與兩個變量有關，證明過程較為復雜，按照有限體積法的量級定性分析。MUSCL類型的格式應用于有限體積法考慮了度量系數，常用形式為

(29)

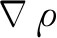
基于以上分析，在坐標變換后如果對原始變量ρ出發(fā)進行重構，應該考慮相鄰網格尺度的變化，滿足精度要求的MUSCL格式為

(30)

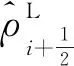
對于均勻流場，在非均勻網格J不為常數的條件下，例如Ji≠Ji-1，其中Ji為節(jié)點i的雅可比行列式，即使?jié)M足ρi=ρi-1，也存在

(31)

由此推斷，重構過程也會引起坐標變換誘導誤差。

Euler方程是擬線性雙曲型方程組，對流項通量、守恒變量和系數矩陣之間具有性質：

(32)

對物理空間自變量(x,y,z)求導：

(33)

同樣對計算空間變量(ξ、η、ζ)求導依然保持這種特性，以ξ為例：

(34)

對應的算子形式有

(35)

代入第4節(jié)中帶有源項的離散等價方程出發(fā)得到算子形式中：

(36)

從式(32)～式(36)推導過程看，沒有任何精度損失。

為應用通量分裂格式，同樣把系數矩陣作為常數移到空間算子內，引入符號

(37)

表示離散點0及其相鄰網格點i的通量，用于編程的算子形式為

(38)

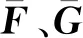
式(38)是在計算空間下的離散算子，在此基礎上針對U應用MUSCL格式：

(39)

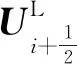
式(39)同直角坐標系下均勻網格的重構形式完全一致，但是二者的精度不同，式(39)達不到標準MUSCL格式的精度。根據上述分析，式(39)乘以坐標變換系數Γ后轉換為計算空間的MUSCL格式才具有直角坐標系下均勻網格的相應精度，Γ本質是非等距插值公式的影響系數。

對于均勻流場，不論參數κ如何取值，均滿足

(40)

因此必然不會產生坐標變換誘導誤差。對于非均勻流場，計算誤差不僅與差分格式有關，還受到流場參數影響，如何驗證還在探索之中。

6 結 論

通過針對不同網格的均勻流算例，展示了坐標變換誘導誤差的普遍性，并對其產生機理進行理論分析，討論了沿著GCL研究路線消除這類誤差存在的難度，提出基于離散等價方程的新思路，構建離散對流項通量的計算方法，推導了針對MUSCL格式的應用策略。提供的算例顯示離散等價方程方法能完全消除坐標變換誘導誤差。