半潛式平臺橫向開閉極限強度的時變可靠性分析

錢呈龍 趙 南 王 璞 李鈞暉 吳劍國

（1.浙江工業(yè)大學 土木工程學院 杭州310023；2.中國船舶科學研究中心 無錫214082；3.中國船舶及海洋工程設計研究院 上海200011）

引 言

半潛式平臺在使用期間由于風浪和海水的作用，必然會受到疲勞和腐蝕的影響，而這些疲勞裂紋擴展以及構件厚度降低會導致平臺結構極限強度減小，使平臺的可靠性隨時間而降低。現(xiàn)今對于船體在疲勞和腐蝕作用下的時變可靠性研究工作較多，例如：劉益清［1］分析計算了船體在疲勞和腐蝕損傷下的可靠性；施興華［2］使用上穿率法，對艦船結構的時變可靠性進行了分析計算。

然而，針對半潛式平臺結構時變可靠性的研究工作相對較少。考慮到隨機變化的腐蝕和疲勞裂紋影響，本文將半潛式平臺結構橫向開/閉的極限強度視為一個隨機過程，采用上穿率法［3］進行分析，通過并聯(lián)系統(tǒng)的方法來計算其時變可靠性，并且與瞬時可靠性作對比分析。

1 半潛式平臺的極限強度時變模型

1.1 疲勞裂紋影響模型

平臺結構構件有效寬度減小主要是由裂紋擴展導致，進而使得結構的極限強度降低。在疲勞分析中，一般引入有裂紋存在的初始條件，在此基礎上，采用Paris-Erdogan方程［4］來建立疲勞裂紋擴展模型：

1.2 腐蝕影響模型

腐蝕作用會使平臺結構構件的厚度減小，導致結構極限強度降低，本文采用一般的腐蝕模型［6］：

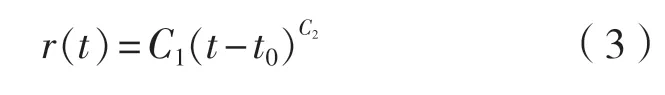
式中， 為t時間內受腐蝕的厚度，mm；C1為年腐蝕率［5］，mm/a；C2的取值范圍是1/3～1，本文取值C2= 1.0； t0為防腐涂料的壽命，a。

1.3 半潛式平臺結構極限強度

半潛式平臺在計算橫向閉合極限承載力時主要考慮的是整體失穩(wěn)，而在計算橫向閉合極限承載力時的整體失穩(wěn)主要體現(xiàn)在底部橫撐的整體受壓屈曲破壞。傳統(tǒng)的Smith法沒有考慮到這一點，因此需要對Smith法作出改進，使之在對半潛式平臺橫向閉合工況極限承載力計算時，考慮底部橫撐的整體受壓。

基于Smith法的基本假定［6］，將半潛式平臺橫剖面離散成普通扶強材、硬角、加筋板3類結構單元，以及橫撐單元。硬角單元在拉伸和壓縮的狀態(tài)下，其破壞模式均為彈—塑性屈服破壞；扶強材單元在受拉時是彈—塑性屈服失效破壞，受壓時有梁柱屈曲、扭轉屈曲以及腹板局部屈曲等多種失效模式；加筋板格單元拉伸時表現(xiàn)為屈服失效，受壓時則為板材屈曲。橫撐的局部穩(wěn)定按照船體規(guī)范的Smith法單元劃分，應力應變關系也按照規(guī)范。整體穩(wěn)定的應力應變關系如下：

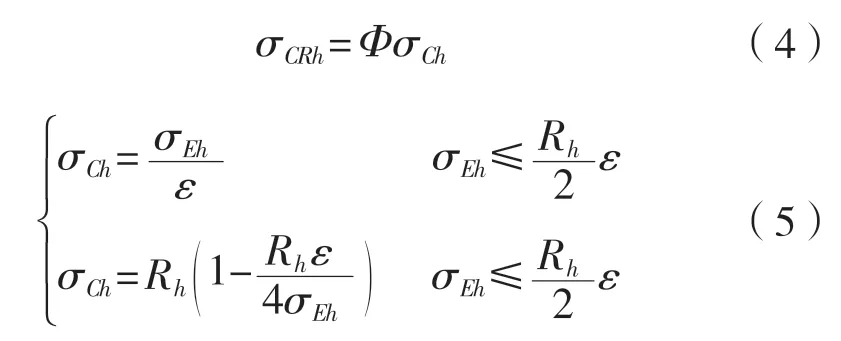
式中：Φ為邊緣函數(shù)， 為橫撐的臨界應力，MPa；

為橫撐的歐拉力，MPa；Ah為橫撐截面面積，mm2。

式中：Ih為橫撐慣性矩，mm4；Rh為橫撐屈服強度，MPa； ε為相對應變；l為橫撐長度，mm。

改進后的Smith法計算步驟是：

（1）將半潛式平臺橫剖面離散成普通扶強材、硬角、加筋板和橫撐4類結構單元，其中前3種單元見CCS規(guī)范［7］，橫撐單元專門針對平臺的橫撐，將其簡化為兩端鉸接，軸心受力的薄壁受壓桿件，考慮其整體穩(wěn)定性。

（2）確定單元的平均應力—應變曲線。

（3）計算得到平臺的彈性中和軸位置，設初始步的曲率增量為χ1；。

（4）每個單元的應變εi都是根據(jù)平面假設計算所得，由平均應力-應變關系計算各單元應力σi。

（5）計算橫撐單元的應變εi，根據(jù)應力-應變關系計算橫撐所屬單元的應力σi。

（6）由橫剖面的力的平衡來確定下一增量步的截面中和軸位置。

（7）通過合計所有單元的貢獻計算相應彎矩Mi。

（8）與前一增量步的彎矩比較Mi-1。若Mi-1＜Mi，則終止計算并定義彎矩極值；否則，以遞增方式增加曲率Δχ并繼續(xù)執(zhí)行步驟4。

與傳統(tǒng)Smith法相比，主要是增加第（5）步關于橫撐單元應力計算，修改Smith法第（8）步。

1.4 受疲勞和腐蝕影響的半潛式平臺極限強度時變模型

平臺的極限強度隨著疲勞裂紋的擴展以及腐蝕的加重會逐年下降，對于扶強材和加筋板單元，由于腐蝕作用厚度隨著時間的增長而減小，其寬度由于疲勞裂紋的擴展而降低，即可得：

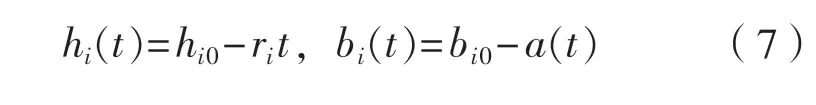
式中：hi0、bi0為扶強材（加筋板）的初始厚度和寬度，mm；ri為扶強材（加筋板）的腐蝕率，mm/a。

對于硬角和橫撐單元，主要受腐蝕作用影響，厚度隨著時間的增長而減小，可得：

在計算可靠性的時候，由文獻［8］可認為平臺結構極限強度服從對數(shù)正態(tài)分布，其均值函數(shù)和標準差函數(shù)由影響極限強度的不確定因素通過Rosenbluth法［9］求得，并且能得出，他們都是關于時間的函數(shù)，因此平臺極限強度應該用隨機過程模型來描述。

2 半潛式平臺的載荷

2.1 靜水彎矩

半潛式平臺的橫向靜水彎矩主要由靜水浮力與重力共同作用產生。參考小水面線船［10］，所受總體靜水彎矩，其 由公式計算得：

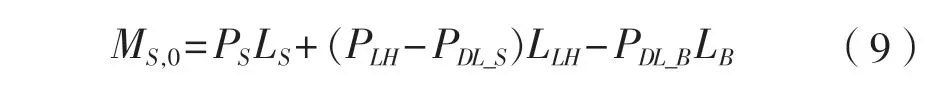
式中：PS為支柱浮力，N；LS為PS至中縱剖面的水平距離，m；PLH為下浮體浮力，N；LLH為PLH至中縱剖面的水平距離，m；PDL_S為支柱與下浮體重量，N；PDL_B為上部結構的重力載荷，N。

2.2 波浪彎矩

波浪彎矩具有長期的不穩(wěn)定性，主要來源有海況發(fā)生概率、波浪譜型、有義波高和載荷傳遞函數(shù)等，它的長期預報是基于海浪短期預報，通常將波浪彎矩模型化為Poisson過程［11］，海洋結構使用期內波浪彎矩極值的累積概率分布函數(shù)可表示為：

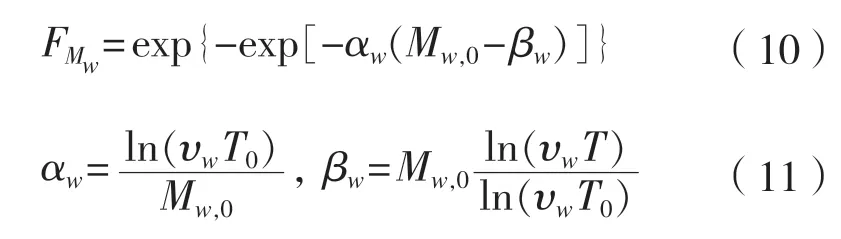
式中：為波浪彎矩的平均達到率； 為平臺使用期限T0內出現(xiàn)的最大波浪彎矩，N·m。

2.3 載荷組合

半潛式平臺總彎矩由靜水彎矩和波浪彎矩組成，傳統(tǒng)的分析方法是將兩者線性相加，但在實際當中，它們一般不會同時以其最大值出現(xiàn)，本文考慮了載荷的組合問題，此時總彎矩表示為：

式中：為載荷折減系數(shù)，詳見參考文獻［12］。

3 可靠性計算

半潛式平臺橫向開/閉極限強度的時變可靠性狀態(tài)方程為：

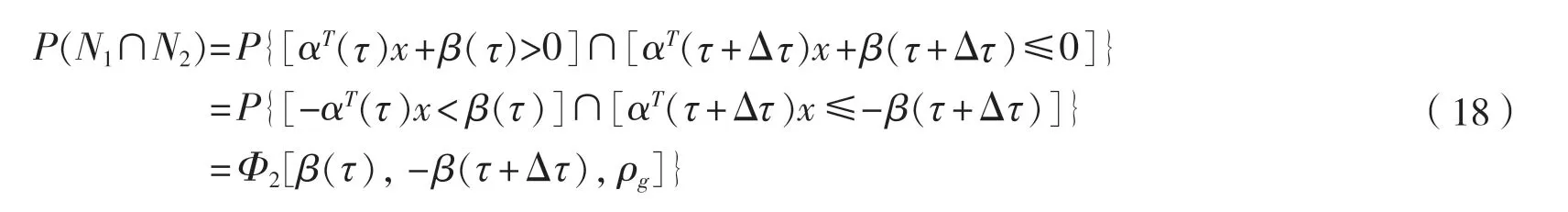
4 實例計算

4.1 平臺主尺度

半潛式平臺主尺寸見表1。

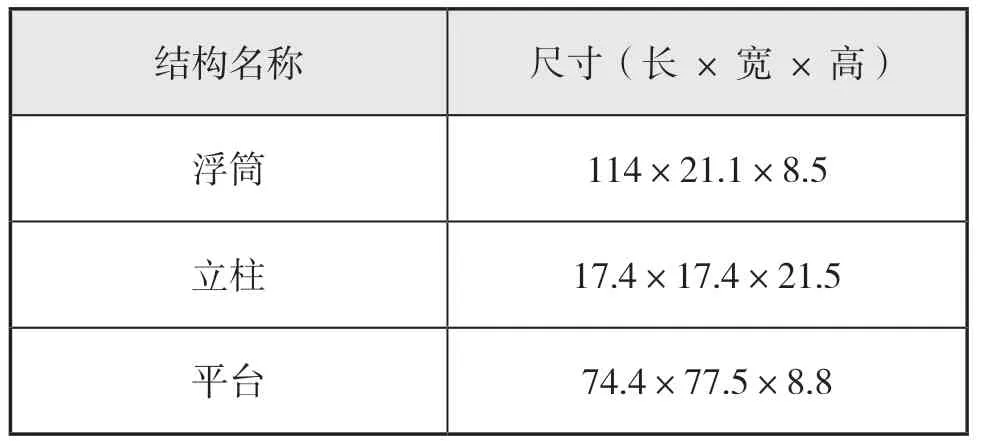
表1 半潛式平臺的主尺度m

4.2 極限強度分析

改進后的Smith法考慮了橫撐結構受壓時會發(fā)生整體失穩(wěn)的情況，能夠更準確地模擬存在橫撐整體失穩(wěn)模型的彎曲極限承載力，采用VB自編程序，對半潛式平臺在橫向開閉工況下的極限彎矩進行計算，并將所得結果與平臺細化模型的有限元數(shù)值模擬結果相比較，在還未考慮疲勞和腐蝕影響下的初始時刻，不同工況下有限元與Smith 法的結果見下頁表2和圖1、圖2。

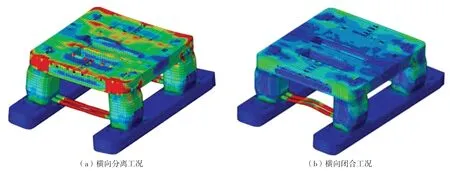
圖1 半潛平臺模型橫向開閉工況極限狀態(tài)示意圖

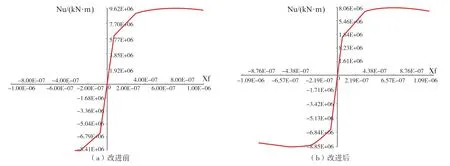
圖2 Smith法不同工況下的彎矩轉角曲線圖

表2 半潛平臺模型在不同工況下極限承載力匯總MN

在橫向閉合工況下，改進前后結果相差30%左右，這是因為此時橫撐受壓發(fā)生整體失穩(wěn)。在橫向分離工況下，改進前后結果僅相差1%，此時橫撐受拉，這說明改進后Smith法結果準確。而在橫向閉合工況下，有限元模型結果與改進后結果相差4%，說明改進后 Smith 法能夠更準確地模擬存在橫撐整體失穩(wěn)模型的彎曲極限承載力。

4.3 極限強度的概率特性

影響平臺結構極限強度的隨機變量概率特征見下頁表3。

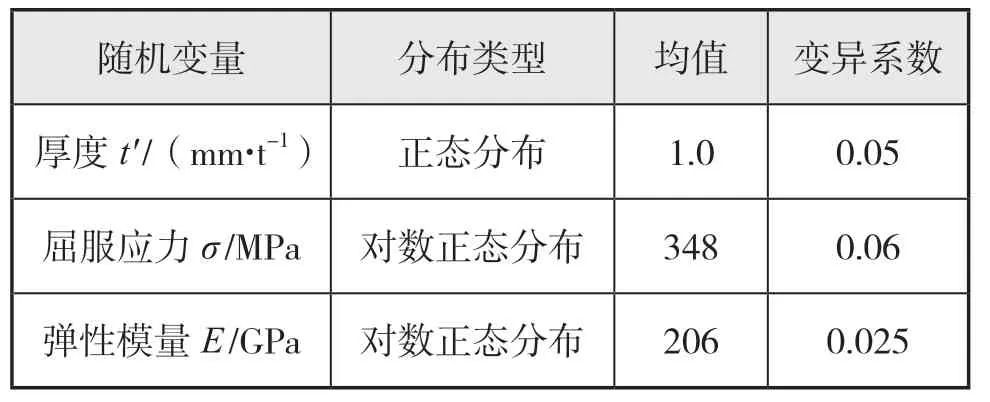
表3 隨機變量概率特征

由參考文獻［13］，得到公式（1）中各參數(shù)，Δσ= 32.6 MPa，C= 1.07-11，a0= 0.5，Y= 1。公式（7）中，本文年腐蝕率C1取值0.1 mm/a。平臺結構極限強度服從對數(shù)正態(tài)分布，在疲勞和腐蝕的影響下，使用自編程序對平臺結構在使用期間的極限強度進行計算，得出均值隨時間改變，并呈現(xiàn)為逐年遞減的趨勢，均值曲線見圖3，而且變異系數(shù)也成遞減趨勢，但是相比于均值變化幅度很小。并且通過計算，當C1取值0.1 mm/a時，結構20年內損失為7.8%；C1取值0.2 mm/a時，結構20年內損失為11.4%；C1取值0.3 mm/a時，結構20年內損失為15.9%。可見，不同的年腐蝕率對極限強度影響較大，進而影響結構可靠度。

圖3 不同工況下結構極限強度均值隨時間變化曲線（C1 = 0.1 mm/a）

4.4 靜水彎矩的概率特性

橫向分離狀態(tài)下靜水彎矩任意運營時間T的均值由式（20）求得，標準差［2］由式（21）求得：

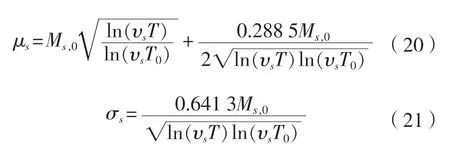
橫向閉合狀態(tài)下靜水彎矩任意運營時間T的均值和標準差由式（22）和式（23）求得：

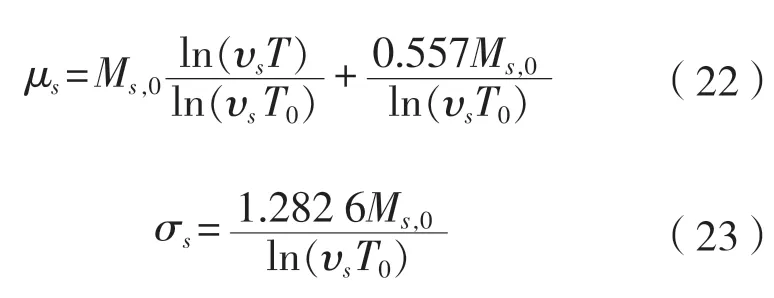
式中：為橫向閉合與分離工況的平均發(fā)生概率［14］，單位為1/d，文中取 =1/60； 平臺的設計使用年限，在本文中取T0= 20 a。并且為更接近實際工程情況，在可靠性計算中將靜水彎矩看作服從正態(tài)分布的隨機變量，不隨時間變化。

4.5 波浪彎矩的概率特性

通過公式（24）和公式（25）求得波浪彎矩在平臺任意使用時間T的均值和標準差：

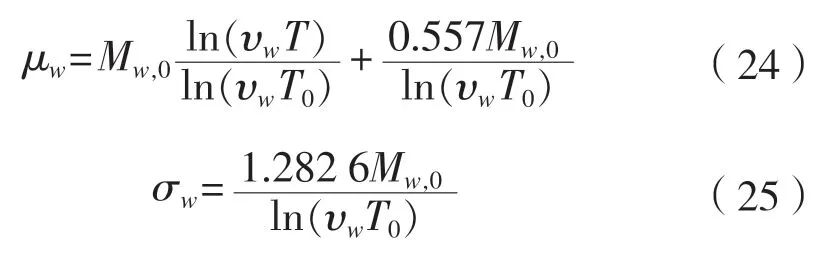
式中：為一次波浪循環(huán)的出現(xiàn)率，假設在平臺使用期限內與海浪的遭遇次數(shù)為108次，即 =108。

按上所述，例如在平臺使用初期（T= 1 a）時，各載荷的概率特征見表4。

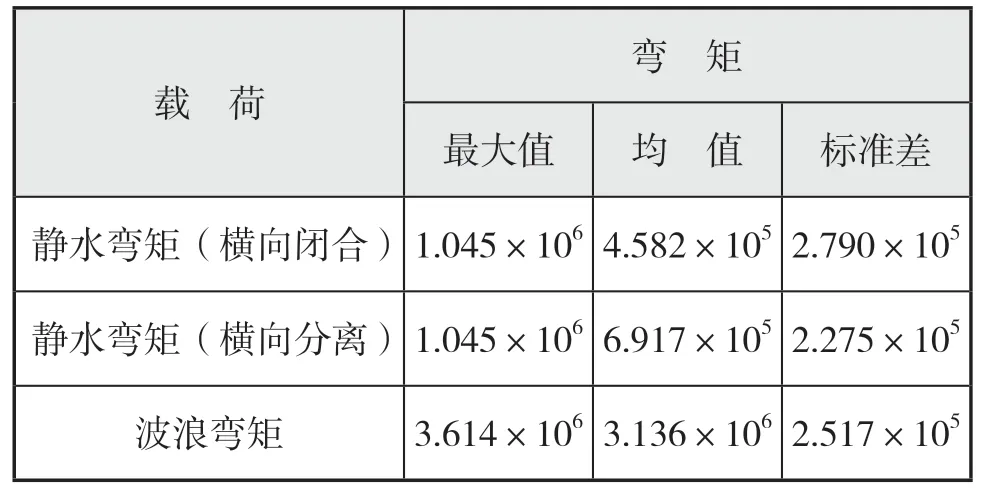
表4 T = 1a時各載荷的概率特征kN·m

4.6 時變可靠度分析

通過上述方法計算平臺結構在疲勞和腐蝕作用下的時變可靠性，采用傳統(tǒng)的JC法對相應的瞬時可靠性進行了計算，并對兩者進行比對分析，考慮到半潛式平臺在使用初期的結構強度很高，故假定其在t= 0時的失效概率為0。

圖4的（a）和（b）分別表示年腐蝕率C1取0.1 mm/a時，橫向分離與閉合工況下受疲勞和腐蝕影響的時變失效概率；圖5的（a）和（b）分別為年腐蝕率C1取0.1 mm/a時，橫向分離與閉合工況下平臺結構可靠性指標的時變值和瞬時值。

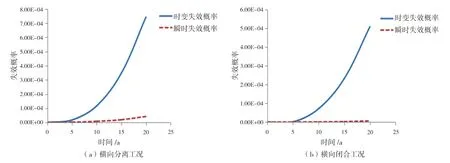
圖4 橫向開/閉極限強度的時變失效概率、瞬時失效概率（C1 = 0.1 mm/a）

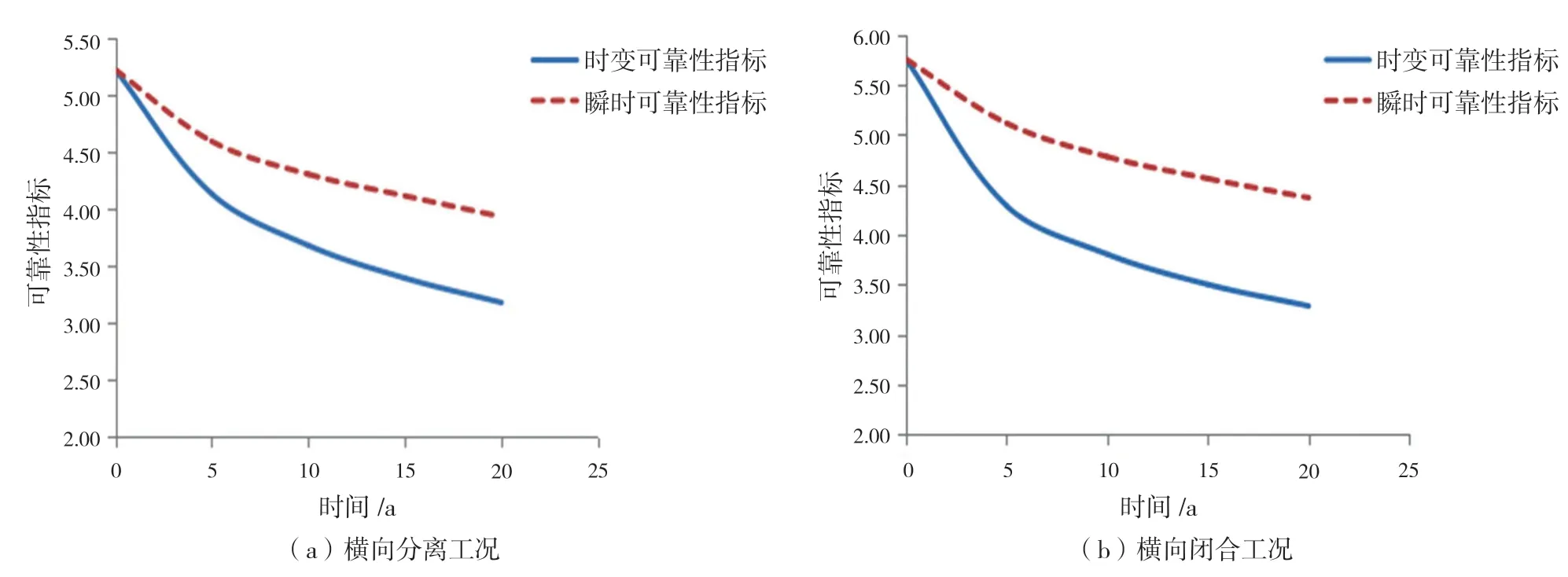
圖5 橫向開/閉極限強度的時變可靠指標、瞬時可靠指標（C1 = 0.1 mm/a）

由圖4可知，在8年以前失效概率的時變值和瞬時值都較小，并且相差不大，這是因為初始疲勞裂紋和腐蝕相對較小，對結構強度幾乎沒有影響。但隨著裂紋的繼續(xù)擴展以及腐蝕的作用，從第10年到20年，時變失效概率已呈曲線增長，并且從第5年開始與瞬時失效概率相差較大，因為后者只是計算在t時刻的瞬間失效，并沒有考慮這個時刻以前或以后的情況。

由圖5可得，時變與瞬變的可靠指標曲線趨勢一致，但是將結構極限強度視為隨機過程后，由此得出的時變可靠度比相應的瞬時可靠度要更低。因此，從安全的角度出發(fā)，使用考慮疲勞與腐蝕作用的時變可靠性方法對平臺結構進行評估更為合理。

針對可靠性結果影響較大的腐蝕率進行敏度分析，在上文年腐蝕率C1= 0.1 mm/a基礎上，增加了在C1= 0.2 mm/a和C1= 0.3 mm/a時，橫向閉合工況下的時變可靠性指標計算結果，并對三者進行對比分析見圖6。

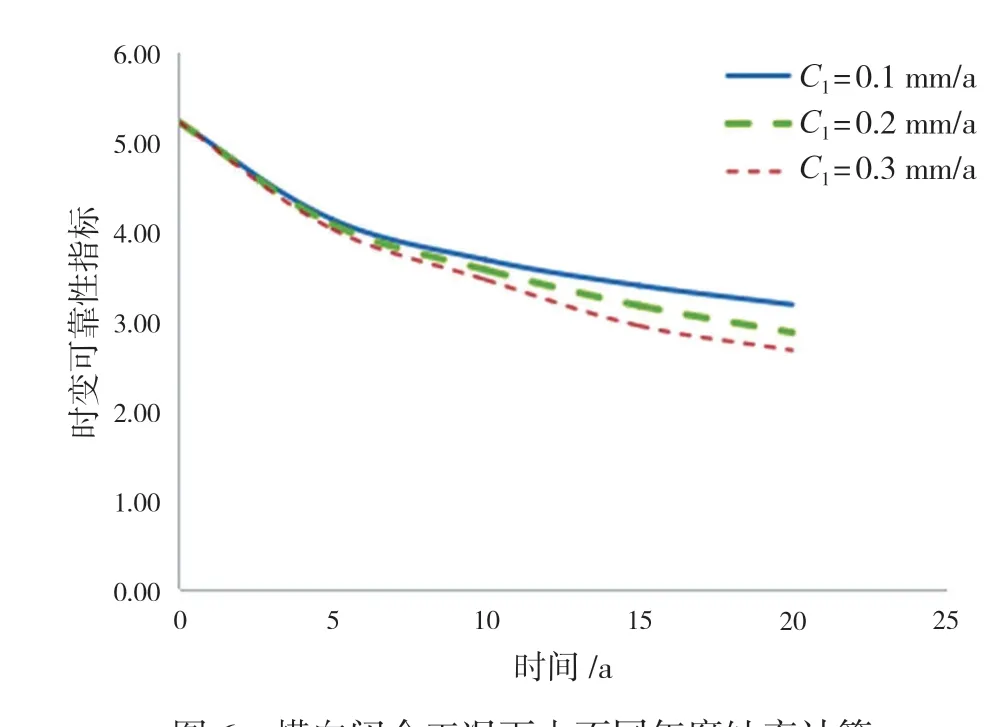
圖6 橫向閉合工況下由不同年腐蝕率計算所得時變可靠指標曲線

由圖6可見，半潛式平臺結構的時變可靠指標受腐蝕率的影響很大，且時間越長，影響程度越大，增加年檢和階段檢驗很有必要。

5 結 語

本文采用改進的Smith法來計算半潛式平臺結構的極限強度，所得計算結果與ABAQUS軟件計算結果相差很小。采用了符合半潛式平臺自身材料屬性和作業(yè)環(huán)境的疲勞和腐蝕參數(shù)，建立了考慮兩者影響的半潛式平臺橫向開閉極限強度時變模型，并且引入隨機過程，使得模型更為準確；使用上穿率法，將隨機過程轉化為隨機變量，并通過傳統(tǒng)的JC法來計算，方法簡便且效率高。

由算例分析可以看出，該平臺的橫向開閉極限強度在10 a以前的時變可靠性變化不大，在10 a之后失效概率成拋物線增長，特別是在15 a之后，失效概率急劇增長。說明此時平臺結構受腐蝕和疲勞裂紋擴展影響嚴重，故建議在15 a以后加強對平臺結構安全評估和維護。