雙波長干涉顯微鏡波長的雙約束標定

劉 乾，黃小津，李璐璐，張 輝

（中國工程物理研究院 機械制造工藝研究所，四川 綿陽621999）

1 引言

作為表面微觀形貌檢測的有效手段，干涉顯微鏡廣泛應用于制造、微電子、生物等多個領域。由于干涉條紋的周期性，所得到的相位壓縮在［0，2π］區間，干涉顯微鏡無法分辨干涉條紋的級次，因而不能分辨表面上大于半波長的高度差異。為確定干涉條紋級次，研究人員提出了相干掃描干涉和雙波長（或多波長）干涉方法。前者通過掃描表面全高度范圍，利用相干包絡確定零級條紋而展開相位［1］；后者通過比較不同波長的相位差異，采用合成較長的拍波拓展了高度范圍限制［2］。這兩種方法的本質都是確定條紋的級次。相較于相干掃描干涉，雙波長干涉顯微鏡無需在表面全高度范圍內掃描，具備速度快、效率高的優勢。

在高度重構過程中，光波長的標定精度是雙波長干涉顯微鏡的精度來源，因此必須對光波長進行標定。一種直接的標定方法是采用光譜儀測量光波長。對于激光光源來講，由于激光線寬非常窄（通常在0.1 nm以下），能夠很精確地確定單個光波長的平均波長，甚至可以直接以名義波長作為實際波長［3-4］。而對于寬光譜的照明（如LED作為光源），則需要采用光譜儀對波長測量后并計算中心波長［5］。此外，在數值孔徑較大的干涉顯微鏡中，物鏡出射的聚焦光線會引起傾斜效應，在標定照明波長之外還需要根據物鏡的數值孔徑計算傾斜因子，得到等效波長［6］。為直接溯源到長度基準上，也可以采用標準件或標準長度對波長進行標定。Liang等在三波長干涉中采用461 nm的標準臺階對三個等效波長進行嚴格標定，并認為濾光片帶寬越窄，波長的校準精度越高［7］。郭彤等以壓電陶瓷掃描器的步長作為長度基準，利用小波方法分別確定三個等效波長，可以達到1 nm的標定精度［8］。上述標定方法利用了長度基準與波長的關聯，以長度整體誤差的最小化為目標。然而，當前的標定方法沒有考慮光波長之間的關系，而這種關系的缺失會給表面高度重構帶來局部誤差（如跳變點），在光滑表面測量時產生不可接受的誤差，嚴重影響標定結果。

本文基于雙波長干涉表面的高度重構誤差分析，在波長與長度基準建立關聯之外，增加了對光波長之間的關聯，提出了一種雙約束的波長標定方法。首先理論分析了高度重構方法及波長誤差對表面高度重構的影響，然后介紹雙約束的波長標定方法，最后以計算機仿真和實驗對標定方法進行了驗證。由于多波長干涉可以視為雙波長干涉的拓展，因此本文主要以雙波長干涉為例展開研究。

2 光波長誤差對高度重構的影響

2.1 表面高度重構

兩個光波長λ1，λ2對應的相位分別為φ1，φ2，假設λ1＜λ2。將兩個相位相減，得到差分位相ΦD′=φ1-φ2，其 對 應 的 拍 波 波 長 為ΛD=λ1λ2/（λ2-λ1）。若 表 面 總 高 度 大 于ΛD/4，則 需 要 對ΦD′在空間展開，展開后的相位記為ΦD。差分相位對應ΛD的級次為：

條紋級次MD由整數I和小數部分F組成，即M=I+F。式（1）得到級次包含了整數部分和小數部分。光相位φ2在0～2π之間，其小數部分可以簡單地計算為F2=φ2/2π，但其整數部分是未知的。根據相位與波長之間的理論關系：M2λ2=MDΛD=h/2，計算表面光相位的整數部分為I2=MDΛD/λ2-F2。由于相位中含有誤差，則計算的I2未必是整數，但可以通過四舍五入將它近似為整數。加上已經得到的小數部分F2，λ2相位的級次可以計算為：

這樣就可以通過M2計算表面高度：

式（3）計算的表面高度是直接從光波長相位得到的，能夠避免差分相位誤差隨波長放大。更進一步地，為了減小表面高度重構誤差，可以構建波長更短的和頻相位［5］，即ΦS=φ1+φ2，其對應的波長為ΛS=λ1λ2/（λ1+λ2）。和頻相位條紋級次的小數部分為FS=φS/2π。從光波長估算和頻相位的級次：

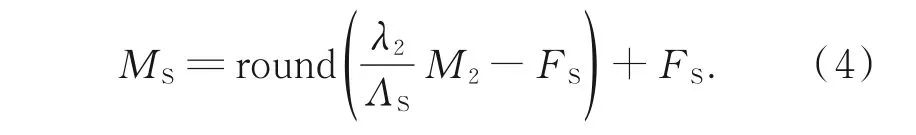
計算表面高度為：

利用式（5）從和頻相位重構的高度能夠獲得比單波長干涉更低的噪聲［5］。

2.2 光波長誤差的影響

光波長誤差對表面高度重構最主要的影響體現在相對高度的縮放上，如式（3）和式（5），表面上不同點之間的高度誤差與波長誤差成正比。實際上，在采用式（2）和式（4）估算級次時，波長誤差也會導致級次估算誤差。假設光波長λi的誤差為Δλi，相對誤差為εi=Δλi/λi。光波長誤差相互獨立，通過偏微分可以計算兩個合成波長的誤差分別為：

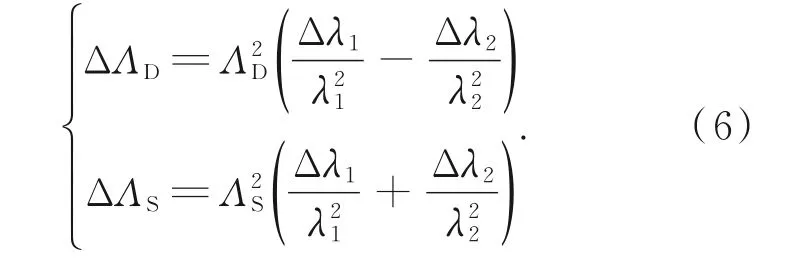
根據式（2）和式（4），λ2相位、和頻相位的級次估算誤差e2，eS分別為：

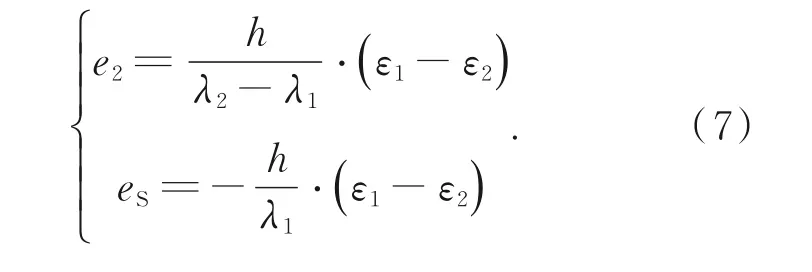
若級次估算誤差e的絕對值小于1/2，則在式（2）和式（5）的四舍五入計算時會被忽略，不會導致跳變誤差；否則，將會產生級次估算誤差，表現為重構表面上半波長整數倍的跳變點。為保證重構表面高度不因波長誤差出現跳變點，需保證式（7）中ε1-ε2=0。該約束的物理意義是，允許標定的光波長存在一定的誤差，但波長誤差之比需要與真實波長比例相等，即λ1/λ2的比值應當與真實波長比值相等。

從和頻相位重構表面高度的誤差，對式（5）進行微分可得：

為 保 證 高 度 的 準 確 性，應 使λ2ε1+λ1ε2=0。該條件的物理意義是，若波長的相對誤差與波長成反比且符號相反，則高度誤差為零。

考察式（7）和式（8）發現，式（7）要求波長誤差同號，而式（8）則要求二者反號。因此，跳變誤差與高度誤差的限定能夠對光波長形成足夠的約束條件，進而獲得確定的波長值。

3 雙約束標定方法

3.1 方法原理

為兼顧整體高度精度并抑制跳變點，本文提出一種雙約束的光波長標定方法。其基本思想是：以跳變點最少的重構結果約束光波長比值，以基準長度約束光波長算術值（以和頻波長為約束對象），如圖1所示（彩圖見期刊電子版）。該方法只需要一個臺階高度標準件（臺階高度h0應小于ΛD/2）。具體流程為：

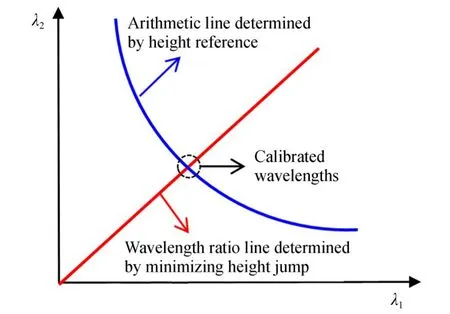
圖1 波長雙約束標定原理示意圖Fig.1 Principle diagram of two-wavelength constraints calibration

第1步：分別以兩種光波長照明，測量標準件平面部分的光波長相位；

第2步：兩個光波長在預先估計的區間λi∈［λi，min，λi，max］內變化，按照式（1）、式（2）、式（4）和式（5）進行表面高度重構，將重構平面校平，判斷跳變點（高度絕對值大于ΛS/4的點），統計每種波長組合下的跳變點數量；

第3步：從跳變點最少的波長組合確定光波長的比值：

這樣可以確定波長比值的約束（圖1紅色直線）。

第4步：分別以兩種光波長照明，測量標準件臺階部分的光波長相位；

第5步：式（2）和式（4）可以轉換成：

因此，根據式（10）得到的相位級次與波長無關，僅由相位和波長比值決定。按照式（5）、式（10）進行表面高度重構，得到以和頻波長級次為計量單位的臺階高度M0。由此可確定和頻波長的數值為：

此時，通過和頻波長約束了光波長的數值（即圖1的藍色曲線）。

第6步：求解式（9）和式（11）組成的二元方程組，得到光波長的數值（圖1中的交叉點）。

通過上述步驟得到的兩個光波長數值具有雙重約束，能夠保證精確的高度溯源，同時也能避免波長標定誤差。

3.2 仿 真

對光波長的標定方法在操作層面進行仿真。光源為綠光和紅光，波長分別為λ1=0.523 μm，λ2=0.625μm，λ1/λ2=0.8368，合成拍波波長ΛD=3.2μm，和頻波長ΛS=0.285μm。生成的相位中加入了標準差為0.03 rad的隨機相位噪聲。

3.2.1 確定波長比值

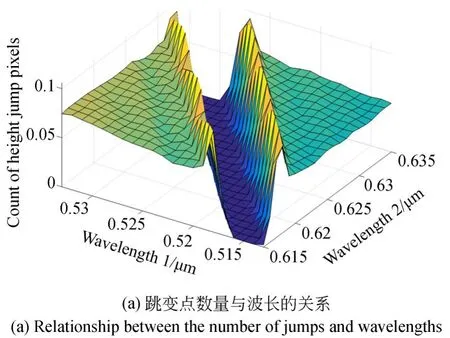
生成平面的整體高度約為7μm。在波長數值±10 nm區間內進行波長組合并重構表面高度。由于被測面為一個平面，理論上校平的平面上每點殘差都應接近于零值。然而，當波長誤差導致表面上存在跳變點時，校平后的表面上存在高度明顯大于ΛS/2的點。作為示例，（λ1，λ2）組合分 別 為（0.515μm，0.615μm）、（0.523μm，0.622μm）時，重構并校平后的表面如圖2所示。對于（0.515μm，0.615μm）的波長數值，比值r=0.8373，接近準確值，因此校平后的表面殘差呈現納米量級的隨機分布，不存在跳變點。對于（0.523μm，0.622μm）的波長數值，比值r=0.8408，表面殘差存在大于ΛS/2的跳變點，數量約為3.6%。得到跳變點的歸一化數量與兩個波長的關系如圖3（a）所示。可以看出，跳變點數量最小的波長組合存在一個明顯的線性關系，與理論分析完全相符。從圖3（a）中尋找每一行的最小值（即跳變點數量最少的點）對應的波長組合。此例中共21個組合數據，其比值分布如圖3（b）所示。雖然波長的比值有所變化，但變化不超過0.5%。此21個波長組合的波長比值平均為0.8371，與真實值0.8368相差小于0.001，表明該方法確定的波長比值具有很高的可信度。

圖2 兩種不同波長組合重構表面的誤差分布。圖中輪廓為箭頭所指行的數據Fig.2 Error maps of reconstructed surface with different wavelengths values.Profiles are extracted from the row indicated with arrows

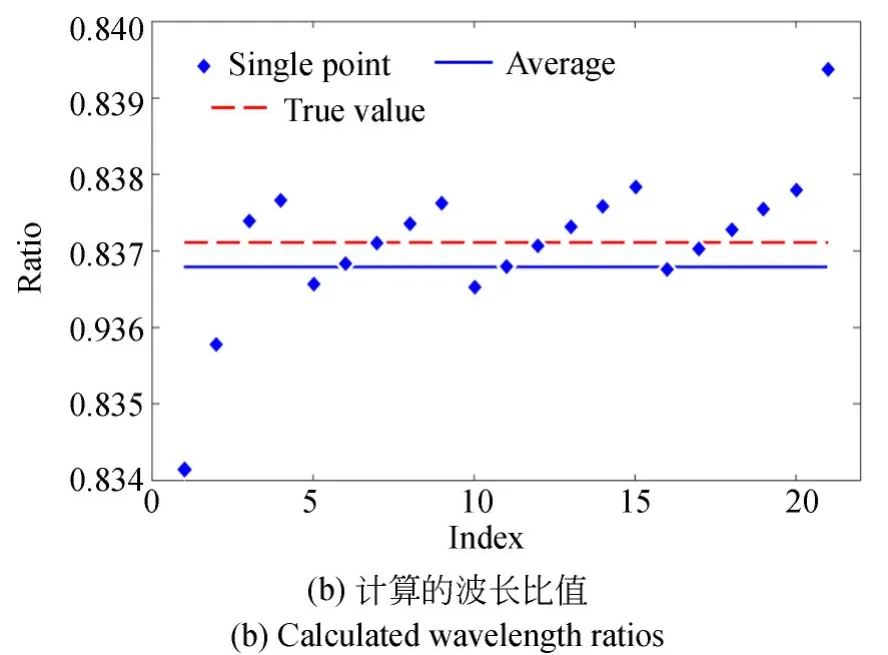
圖3 波長比值的仿真結果Fig.3 Simulation results of wavelength ratio

3.2.2 確定波長

以高度為0.7μm的臺階為測試表面，加入傾斜項模擬實際情況。生成光波長對應的相位，并加入標準差為0.03 rad的高斯白噪聲。如果以估計的光波長數值進行表面重構，可能會因為估計的偏差導致臺階表面存在跳變點，從而影響重構的臺階高度。本方法中首先確定了波長的比值，在表面重構時不依賴具體的波長數值，從而避免臺階表面發生跳變。按照式（11）從光波長相位中重構表面，得到以和頻相位級次為單位的表面高度分布，臺階的表面沒有跳變點，如圖4（a）所示。對臺階底面進行校平，如圖4（b）所示，進行臺階上下表面高度分析，得到臺階高度為4.917。根據已知的臺階高度，通過式（11）反算和頻相位波長為0.285μm。加上波長比值的約束，可以計算兩個波長為λ1=0.5231μm，λ2=0.6249μm。該標定的數值與真實值僅相差0.1 nm，具有非常高的精度。

圖4 重構的臺階表面Fig.4 Reconstructed step surfaces

為驗證本方法的魯棒性，通過仿真研究了波長標定結果與相位噪聲的關系。標定時采用12次結果的平均值。相位噪聲為高斯隨機分布，以噪聲的標準差表征噪聲強度，得到波長相對誤差與噪聲強度的關系如圖5所示。雖然波長標定誤差隨著噪聲的增加而變大，但對于干涉測量來講，0.05 rad的噪聲強度已基本達到上限，此時的標定誤差仍小于0.1%。這表明本方法能夠容忍噪聲的影響。

圖5 波長標定誤差與相位噪聲的關系Fig.5 Wavelength calibration error as function of phase noise

雙約束波長校準方法的精度高，其主要原因在于：（1）建立了兩個約束條件限定光波長數值；（2）以更短波長的相位重構表面，有效抑制了相位誤差的放大；（3）重構表面時以波長比值帶入運算，避免了因波長估計偏差引起臺階表面的跳變點，保證了重構的臺階精度。

4 實驗

4.1 實驗條件

實驗使用一臺配有多光源的干涉顯微鏡對提出的標定方法進行了驗證。干涉顯微鏡配有綠光和紅光LED。選用20×的Mirau型干涉物鏡，測試范圍約為0.85 mm×0.71 mm。單個光波長照明下，每次采集9幅π/2相移干涉圖。選用一種可補償相移誤差算法從單波長干涉圖中提取相位，該算法能夠抑制掃描器誤差和環境振動對測量的影響［9］。這里將兩種光波長照明下采集9×2幅干涉圖并重構表面稱為一次測量。作為對比，先采用光譜儀測量LED的光譜如圖6所示。綠光LED光譜的半高寬約為31 nm，紅光LED光譜的半高寬約為14.5 nm。采用重心法計算其平均波長分別為λ1=532.69 nm，λ2=610.92 nm。根據重心法得到波長數值，其合成的拍波波長約為4.16μm。

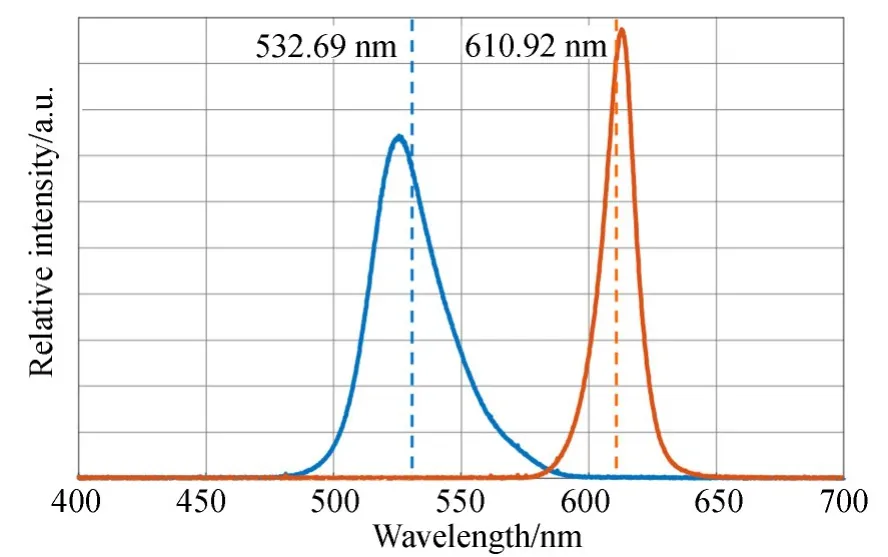
圖6 干涉顯微鏡的綠光與紅光光譜Fig.6 Spectra of green and red LEDs in interference mi?croscope

4.2 波長標定

選用一個標稱1.8μm的臺階作為標定長度基準。臺階計量的高度為1.768μm±10 nm（k=2）。首先，對臺階的平面部分進行8次測量，計算得到兩個光波長的相位。分別在λ1為（533±15）nm，λ2為（611±7）nm的范圍內，以1 nm為間隔的波長組合對表面高度進行重構，并計算表面跳變點數量。其中一次重構表面的跳變點數量如圖7（a）所示，其對應的波長比值如圖7（b）所示。8次波長比值的檢測結果平均值為0.8719。

圖7 波長比值的標定結果Fig.7 Calibrated wavelength ratios

然后，對臺階部分進行12次測量，用于確定和頻波長的數值。重構表面以和頻相位的級次表示，其中一組校平后的臺階表面如圖8所示。為避免臺階交界處局部不平整導致的臺階高度誤差，對臺階交界處1/3之外的平面進行高度分析。12次測量得到臺階高度的平均值為11.96，那么對于式（11），M0=11.96。結合波長比例和波長算術值的約束關系，計算得到λ1′=552.9 nm，λ2′=636.6 nm。該結果與光譜儀得到的光波長偏差較明顯，此偏差主要源于物鏡的傾斜效應。

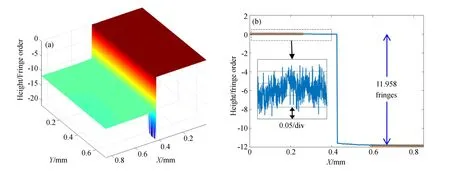
圖8 校平后的臺階表面（a）及輪廓（b）Fig.8 Leveled surface（a）and profile（b）of step

為獲得高精度結果，共標定12次并取標定結果的平均值。12次標定得到的臺階高度如圖9（a）所示，除了其中一次帶有明顯差別（仍在3σ范圍內）外，其他11次標定結果的吻合度相當高。12次得到的臺階高速平均值為11.96倍的和頻波長級次。12次波長標定結果如圖9（b）所示，取12次平均值得到λ1=553.5 nm，λ2=634.8 nm，標定結果的標準差均在亞納米范圍，具有非常高的精度。該標定結果與光譜儀測定的等效波長具有約2～3 nm的偏差，由此表明直接采用光譜儀進行波長標定存在明顯的誤差。

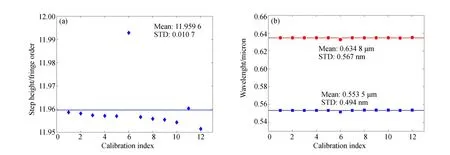
圖9 臺階高度（a）與波長數值（b）的12次標定結果Fig.9 Calculated step heights（a）and wavelength values（b）of 12 calibrations

4.3 刻線深度測量驗證

為驗證波長標定效果，采用雙波長干涉顯微鏡對一個刻線板的溝槽進行測量。對溝槽進行8次測量，采用4.2節標定的波長數值對表面高度進行重構，其中一次測量的表面高度如圖10所示。在刻線板的特征標記位置處（圖10（a）的箭頭所指部分），溝槽的標稱深度為0.7μm，其輪廓如圖10（b）所示。按照3W原則對底部區域取平均，此次測量的高度為0.7533μm。8次測量結果的平均值為0.7530μm，標準差為0.38 nm，如圖11所示。同時采用干涉顯微鏡的白光垂直掃描干涉（VSI）模式與擴展相移干涉（ePSI）模式對溝槽進行了16次平均測量，標記處的深度分別為0.7535，0.7481μm。本方法測量的溝槽深度值與兩種模式測量結果的最大偏差分別為0.5，4.9 nm，表明所標定的波長數值具有非常高的準確性。

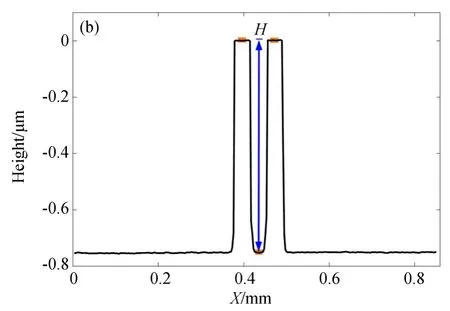
圖10 測量的溝槽表面（a）與特征標記處的輪廓（b）Fig.10 Measured grooved surface（a）and profile（b）in?dicated with symbols

圖11 溝槽深度的8次測量結果Fig.11 Measured groove depth in 8 measurements

5 結論

本文基于表面跳變誤差與高度誤差的約束，提出了雙波長干涉測量的雙約束標定方法。通過確定波長比值與波長算術關系對波長數值進行約束求解，進而得到準確的等效波長，為表面高度重構提供基礎參數。標定只需要一個標準高度的臺階即可完成，但比傳統的臺階高度檢測多了一個約束，提高了波長標定精度。仿真與實驗結果表明，波長標定精度可達到亞納米量級，實際測量表面高度的精度優于0.5%或更高。雖然本方法只對雙波長光干涉展開討論，但也可拓展到三波長干涉，或者應用于數字全息技術。