基于ANSYS 的機床床身尺寸優化設計

房久劍，李天箭

（200093 上海市 上海理工大學 機械工程學院）

0 引言

機床的優化設計方法有很多，美國 Catholic大學的 Bianchi G、Iowa 州立大學的Vance J M、ISU 研究中心的Yeh T P、Michigan 大學的 Jiang T和 Chiredast M 都分別提出了幾種關于機床優化設計的方法：一是將控制技術和虛擬現實技術相結合；二是對零部件進行建模并拓撲優化的方法；三是利用有限元方法進行參數化設計[1-3]。本文通過以某一機床床身基礎結構為模型進行有限元分析結構尺寸參數對最大相對變形和固有頻率的影響，來確定某一最優的尺寸參數，進而來改進機床床身結構性能。

1 參數化三維建模

機床的零部件較多，但是對整機結構性能影響較大的零部件有機床床身、立柱、主軸箱以及工作臺和滑鞍等，而本文主要是對機床床身進行結構性能的分析，因此對機床床身模型進行簡化。在ANSYS Workbench 中的DM 模塊建立機床床身三維模型，如圖1 所示。簡化的床身模型尺寸為：1 350 mm×900 mm×310 mm。

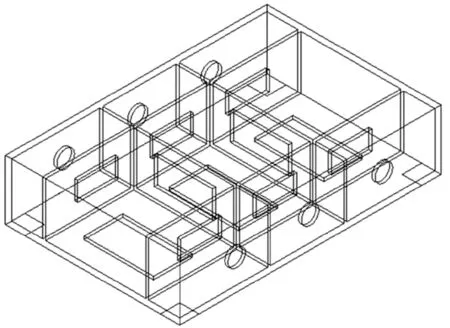
圖1 DM 床身三維模型Fig.1 DM 3D bed model

根據秦大同、謝里陽主編的《現代機械設計手冊》第1 卷第2 篇，零件結構設計中提及的灰鑄件外壁厚、內壁厚設計尺寸，將原始的模型外壁、內部筋板厚度分別設為12 mm 和10 mm。

2 機床床身有限元分析

2.1 材料屬性

機床床身的材料為灰鑄鐵，彈性模量E=1.1×1011Pa，材料密度ρ=7.2×103kg/m3，泊松比v=0.28。

2.2 網格劃分

將機床床身的三維模型利用有限元網格劃分成四面體單元模型，如圖2 所示。網格總共包含92 187 個節點，46 401 個單元。

圖2 四面體網格Fig.2 Tetrahedral mesh

2.3 載荷和約束

機床工作時，各個部件所受的力各不相同，機床床身所受到的力方向也各不相同。機床床身主要受主軸箱的自重、主軸箱刀具的徑向力、工作臺的自重以及橫向的摩擦力、立柱的自重等，所以在機床床身上面簡單地施加XYZ 方向各100 N 的均布載荷，底面四角固定，如圖3 所示。

圖3 載荷與約束Fig.3 Load and constrain

3 尺寸優化設計

3.1 優化數學模型的建立

結構優化設計中，設計變量為待確定的一些參數，這些參數反映了結構的形狀大小、性能優劣等。在ANSYS Workbench 結構優化設計中所設定的設計變量不能多于60 個，各變量之間可以用數學表達式表示，簡稱參數耦合。設計變量通常用x1，...，xn表示，并構成一個向量[4]，即

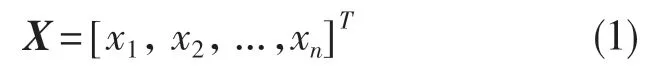
本文設計變量為外壁厚depth（x1）和內部筋板厚度rib（x2），即X=[x1，x2]T，單位：mm。選擇導軌最大相對變形y1和1階固有頻率f0為多目標函數[5]。

約束條件：

考慮可鑄造性的尺寸厚度的上下限約束，設置外壁尺寸為8～24 mm，筋板尺寸為6～22 mm。

綜上，床身結構尺寸優化數學模型為

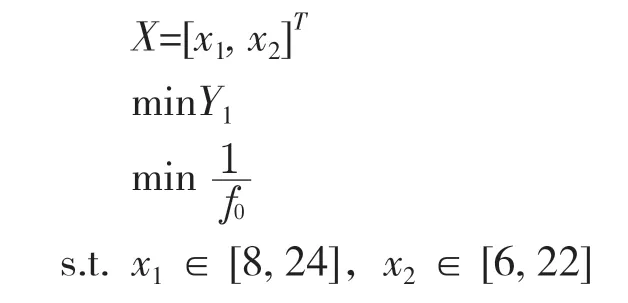
3.2 響應面分析

對設計變量參數進行設置，通過ANSYS Workbench 中Response Surface 模塊對機床床身進行響應面分析，得出如圖4、圖5 所示的最大變形和1 階固有頻率的響應面分析結果，圖6 所示為各參數變量對機床床身最大變形、最大應力和1 階固有頻率的靈敏度分析[6]結果。

圖4 最大相對變形Fig.4 Maximum relative deformation

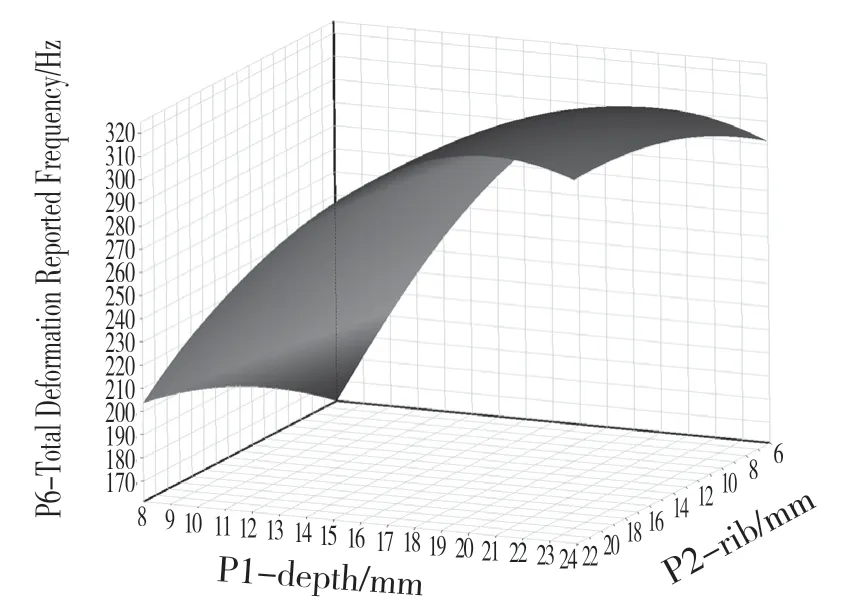
圖5 1 階固有頻率Fig.5 First order natural frequency

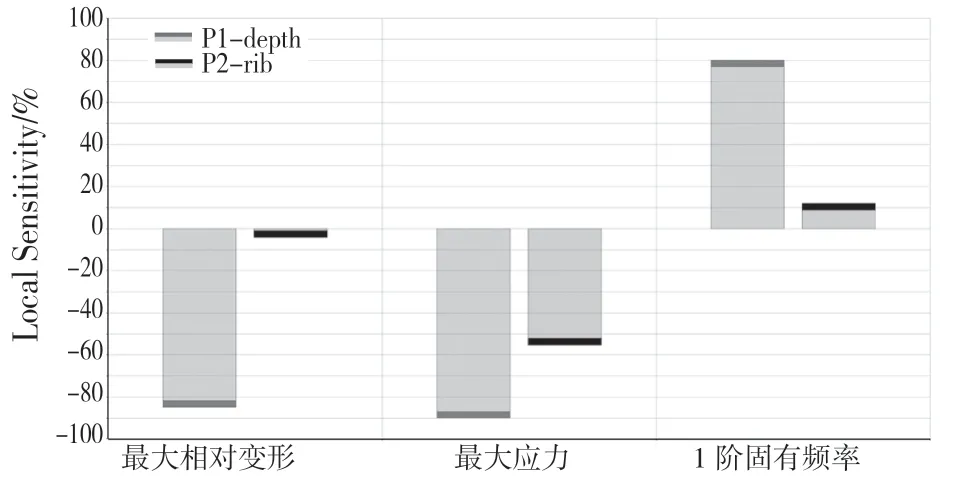
圖6 靈敏度分析Fig.6 Sensitivity analysis

通過外壁厚度depth 和筋板厚度rib 對最大應力、最大相對變形和一階固有頻率的響應面分析和靈敏度分析，可以得出外壁厚度和筋板厚度對結構動靜態性能（應力、變形和一階固有頻率）都有影響，其中外壁厚度變化對結構動靜態性能的影響高于筋板厚度變化對結構動靜態性能的影響。且隨著外壁厚度和筋板厚度的增加，機床床身的最大相對變形隨之減小，1 階固有頻率隨之增加。

3.3 優化分析

利用ANSYS Workbench 優化模塊對機床床身尺寸進行優化，得如圖7 所示3 組候選點（最優解）以及靜態分析的最大相對變形迭代過程（圖8）和模態分析的1 階固有頻率迭代過程（如圖9）。可得最優解為外壁厚度depth=21.372 mm，筋板厚度rib=20.218 mm。考慮到實際鑄造工藝，將最優解近似等效為21 mm 和20 mm。

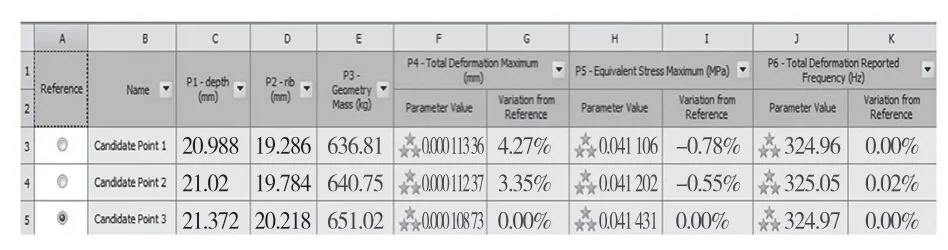
圖7 優化后的候選點Fig.7 Optimized candidate points

圖8 最大相對變形迭代Fig.8 Maximum relative deformation iteration

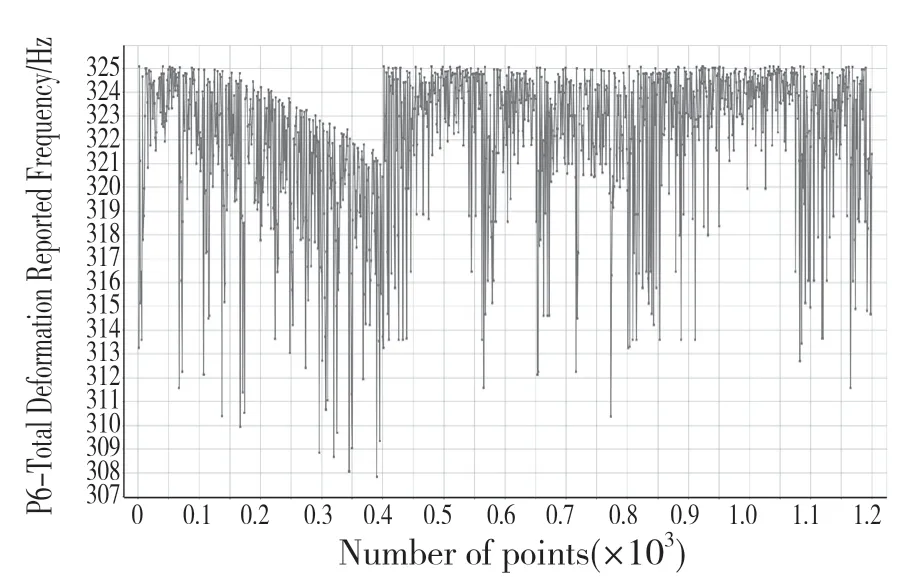
圖9 1 階固有頻率迭代Fig.9 First natural frequency iteration

對此機床床身進行靜力學分析和模態分析[7-8]，得到如圖10—圖13 所示的結果，將數據結果統計成表1 所示。

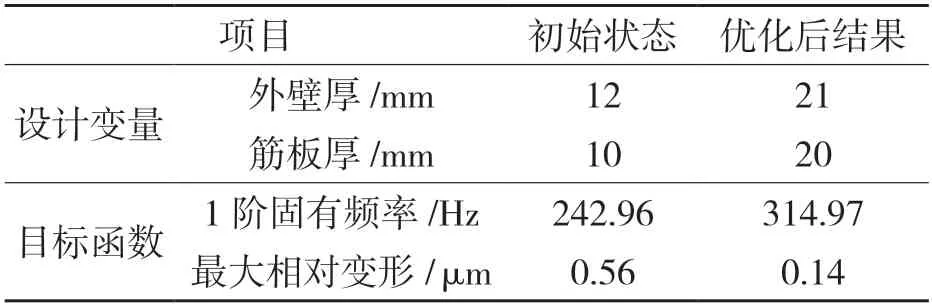
表1 優化前后對比Tab.1 Comparison before and after optimization

圖10 優化前最大變形Fig.10 Maximum deformation before optimization

圖11 優化后最大變形Fig.11 Maximum deformation after optimization

圖12 優化前1 階固有頻率Fig.12 First natural frequency before optimization

圖13 優化后1 階固有頻率Fig.13 First natural frequency after optimization

對比優化后尺寸（外壁厚度21 mm，筋板厚度20 mm）與優化前尺寸（外壁厚度12 mm筋板厚度10 mm）的各結果可知，優化后機床床身最大相對變形由0.56 降至0.14，大大提升了機床床身的靜態性能。1 階固有頻率由242.96 Hz提升至314.97 Hz，提升了29.6%，大大提升了機床床身的動態性能，從而實現了機床床身的尺寸優化設計過程，對機床整體的性能提升有所幫助。

優化前后，機床床身的前6 階固有頻率的對比折線圖如圖14 所示。從圖14 可以直觀地看出，優化后的床身尺寸結構的各階頻率都高于優化前對應的各階頻率。這也證實了前面所述的優化后床身尺寸，可以提升機床床身的動靜態性能。

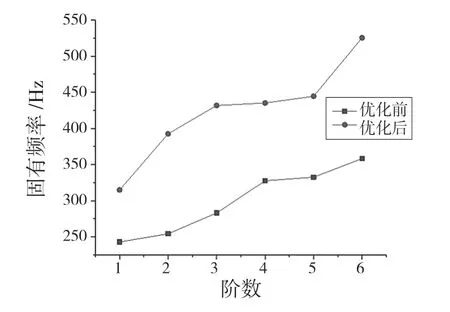
圖14 前6 階固有頻率對比Fig.14 Comparison of the first six natural frequencies

4 結論

（1）本文針對機床床身不同尺寸對其結構性能的影響，對機床床身進行了結構設計，得出最優的機床床身尺寸結構優化設計方案。通過響應面分析、優化分析，可以得出機床床身的外壁厚度和筋板厚度對機床床身結構性能都有一定的影響，且外壁厚度對其影響更為顯著。

（2）通過比較優化前后的最大相對變形和其前六階固有頻率，得出優化后的尺寸參數可以使機床床身結構性能達到最優。

（3）機床床身尺寸結構優化的方法同樣適用于優化立柱和主軸箱等重要的機床零部件，為機床整體優化提供了參考。