基于振動監測的混凝土重力壩模態識別結果的評價研究

毛昊然，程 琳*，陳詩怡，楊 杰，袁興國

（1.西安理工大學 西北旱區生態水利工程國家重點實驗室培育基地，陜西 西安 710048；2.華能瀾滄江新能源有限公司，云南 昆明 650214）

0 引言

我國處于環太平洋地震帶與歐亞地震帶之間，很多大型水利工程都位于強震區，地震頻發。例如，位于滇西北川西南活動構造區的龍開口重力壩曾受過Ⅷ度地震影響[1]；鮮水河—滇東地震帶的金沙江魯地拉重力壩多次發生7級以上的地震，最高震級為8級[2]。混凝土重力壩是水利工程常用的壩型之一，國內外對混凝土重力壩遭遇地震而發生損傷破壞的案例也多有報道。在國外，印度的Koyna重力壩1967年經歷了6.5級水庫誘發地震，下游折坡點高程附近的上、下游壩面出現大量水平裂縫，并有貫穿性裂縫[3]；英國的Blackbrood重力壩1957年經受了6.4級地震，大壩下游面出現裂縫[4]。在國內，2013年四川蘆山地震，震中附近的勝利電站混凝土重力壩左岸巖石松動，壩體內部嚴重滲漏；寶興水庫混凝土壩下游右壩尖發生山體滑坡，嚴重影響了大壩安全運行[5]。通過系統識別（主要是模態識別）來獲得表征結構動力特性的模態參數，以分析地震前后混凝土重力壩結構動力特性的變化情況，以便進行結構的震損評估、模型修正和抗震分析是保障強震區混凝土重力壩結構安全、指導大壩運行管理和修復、提高大壩抗震性能等均具有重大意義。在各種模態識別方式中，利用振動觀測系統采集的大壩結構在地震和環境激勵下的原型振動觀測數據，來識別混凝土重力壩結構的模態參數，無需進行額外人工激勵，節約大量成本，符合大壩實際運行工況以及邊界條件，可以獲得真實反映結構工作狀態下動力特性的特征參數[6]。

1962年，我國在新豐江大壩上布設了第一個強震觀測臺[7]。陳厚群[8]院士精選收錄了我國1966—1995年間758條水工建筑物強震記錄中的299條重要強震記錄，并出版書籍供科研工作者查閱和研究。張立飛等[9]人基于強震觀測數據對龍羊峽拱壩進行了模態分析，并與以往的模型試驗、理論計算進行對比，發現對原型強震記錄進行分析得到的模態參數更符合大壩實際動力參數。徐辰奎[10]以水口重力壩地震中的原型觀測數據作為依據，采用功率譜峰值法、隨機減量和時域ITD法、有限單元法對其自振特性進行研究。程琳等[11]提出了基于Hankel矩陣聯合近似對角化的運行模態識別方法，并根據地震觀測記錄對某重力壩的模態參數進行了識別。在國外，韓國水資源公司（K-Water）在2006年開發了一套大壩地震觀測系統，用于監測壩體的環境振動和地震[12]。Alves等[13]采用分段方式基于程序MODE-ID對美國某拱壩1994年的Northridge和2001年的San Fernando的地震記錄進行了分析。混凝土重力壩作為一種自由度高的超靜定水工建筑物，模態密集，受工作環境影響嚴重，使得對結構的模態分析較為復雜。就地震觀測的系統識別而言，由于地震性質復雜，其存在的優勢和劣勢頻率成分給結構模態參數識別帶來困難。而環境振動監測數據主要用于房屋、橋梁等建筑的模態識別，在壩水體系中的應用還較少。且因為環境振動振幅較小，易受噪聲影響，使模態分析時虛假模態剔除和系統定階有很大的困難。

本文介紹了四種常用模態識別方法的基本理論，并以水口重力壩為例，利用不同方法對大壩地震觀測數據和環境振動觀測數據進行模態識別。通過識別結果的相互比較，分析基于地震觀測或是環境振動觀測進行模態識別的優劣性。

1 基于振動觀測結構系統識別方法

基于原型觀測的結構模態識別方法可以分成考慮輸入和輸出的（IO）方法和僅考慮輸出的（OO）方法。在各類模態識別方法中，自回歸各態歷經（ARX）模型、頻域分解（FDD）、特征系統實現算法（ERA）和隨機子空間識別（SSI）最為常用。其中ARX模型是一種IO類的方法，FDD是一種OO類的方法，而ERA和SSI都有IO和OO兩個不同的版本。以下對這四種識別方法的基本原理進行了介紹。

1.1 ARX模型

ARX模型可用下式表示:

式中，x（k-1）為輸入向量；y（k）為輸出向量；e（k）為誤差。A（q）、B（q）是關于q的多項式。

解A（q）=0的根后，即可求出各階振型頻率fk以及阻尼比ξk:

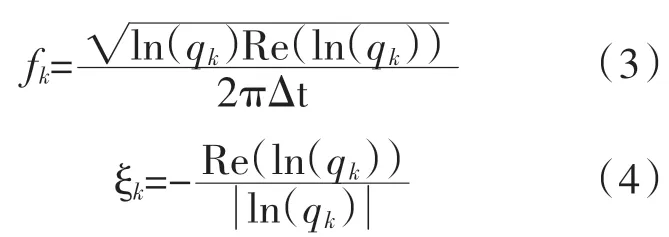
其中，qk是A（q）的特征值；Re（*）是*的實部。

1.2 FDD

FDD由峰值拾取法（PP）發展而來，在使用中，僅需拾取峰值即可。它的優點是不會產生虛假模態。FDD法假設系統受到白噪聲激勵，輸出響應信號功率譜密度函數為:

式中，Gxx（jω）是輸入信號的功率譜密度矩陣；Gyy（jω）是輸出信號的功率譜矩陣；H（jω）是頻響函數矩陣；上標*表示伴隨矩陣，上標T表示轉置矩陣。

方程（5）可轉化為:

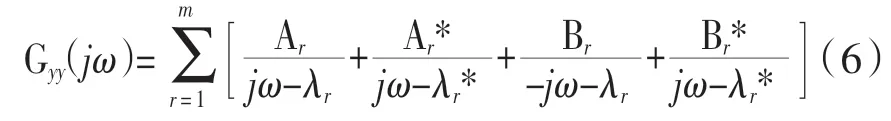
Ar是所得假定頻響函數矩陣；Br是假定頻響矩陣；λr和λr*分別是系統極點和伴隨矩陣的系統極點。

根據各通道測量的響應信號，計算相應的功率譜密度矩陣，然后進行奇異值分解。

利用Ur即可得到模態振型的估計值。

1.3 ERA

考慮噪聲的輸入輸出離散狀態空間模型可用下式表示:

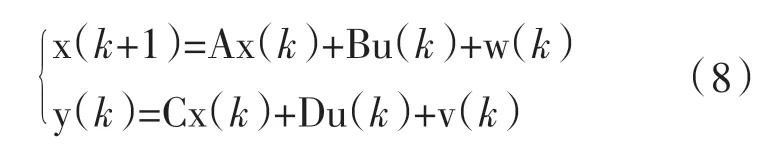
A、B、C、D分別為狀態矩陣、輸入矩陣、輸出矩陣、傳遞矩陣，x（k）為狀態向量，y（k）為輸出數據，u（k）為輸入數據，w（k）、v（k）為白噪聲。

不考慮輸入，僅考慮輸出信號時，離散狀態空間模型可以改寫為:

ERA-IO利用Kalman濾波器（OKID）方法計算得到脈沖響應函數h（k），構造Hankel矩陣:

對H（k-1）進行奇異值分解后，通過一系列處理和變換，可以獲得對A、B、C、D的合理估計，便是系統的最小實現，以此為基礎可以進一步得到結構的模態參數。OKID方法具體介紹以及模態參數的算法可參考文獻[14]。

ERA-OO是利用自然激勵技術（NExT）得到環境振動激勵下結構響應的互相關函數來代替結構的脈沖響應函數，再進行類似步驟得到結構模態參數[15]。

1.4 SSI

SSI-IO算法是根據輸入輸出離散狀態空間模型（8），將輸入輸出數據組成Hankel矩陣，計算矩陣的行空間投影，并對投影進行奇異值分解，得到可觀測矩陣和狀態序列的卡爾曼濾波估計，進而確定系統矩陣A、B、C、D。該方法的具體介紹見參考文獻[16]。SSI-OO算法，由僅考慮輸出的離散狀態空間模型（9），定義輸出協方差矩陣為數學期望。

構造托普利茲矩陣如下:

將矩陣T1|i分解為T1|i=OiTi，其中Oi為可觀測矩陣，Ti為擴展可控矩陣，對其進行奇異值分解得:

根據不為0的奇異值個數確定系統階次，再根據U1、S1計算出系統矩陣、輸出矩陣，最終得出系統的模態參數，該方法的具體介紹見參考文獻[17]。

2 混凝土重力壩模態識別的工程經驗

表1 是根據相關學者研究成果整理的不同混凝土重力壩模態識別結果的統計。利用最小二乘法對壩高與第一階自振頻率進行線性擬合，得到第一階自振頻率f和壩高h的線性經驗關系式為:

表1 國內外部分重力壩系統識別結果的統計

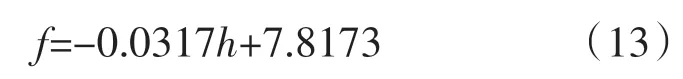
該線性擬合公式的擬合優度R2=0.5548，擬合結果如圖1所示。

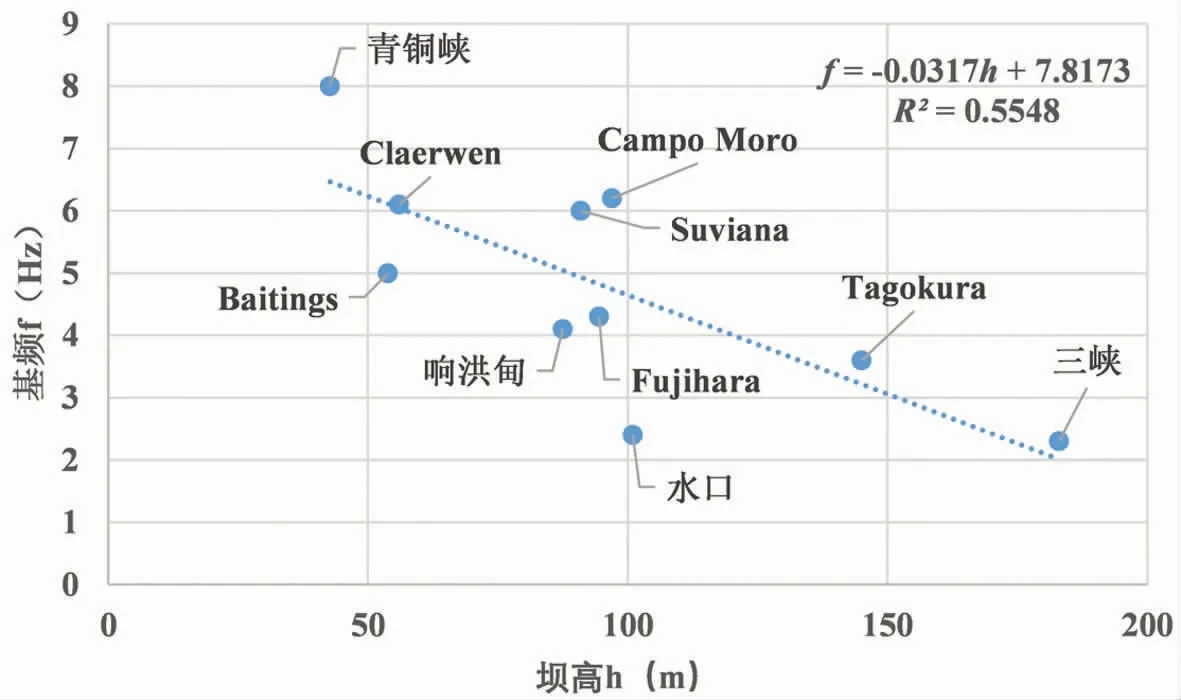
圖1 壩高與第一階頻率線性擬合圖Fig.1 Linear fitting diagram of dam height and first-order frequency

3 水口重力壩及其振動觀測系統

福建省水口水電站位于福建省閩江干流中游，是華東地區最大的水電站，于1993年建成，是以發電為主兼有航運、過木等綜合利用的大型水利工程。混凝土重力壩全長870.0m,高101.0m，正常蓄水位為65.0m，設計水位為65.0m，校核洪水位為67.7m，電站裝機容量為1400MW。該工程臨近臺灣海峽強震帶，大壩上共布置了7個強震儀進行監測，自由場設在右壩肩基巖上，如圖2（a）所示。本文選用19#壩段上的四個強震儀SE1-SE4的觀測數據進行分析研究。這些強震儀共有9個觀測通道，布置情況如圖2（b）所示。

圖2 水口重力壩強震儀布置圖Fig.2 Layout of strong motion instrument for Shuikou gravity dam

自2003年大壩強震觀測系統的改進以來，水口庫區地震監測臺網共記錄到2級以上（含2級）地震50次，3級以上（含3級）地震23次，其中，最大的是2008年3月6日的古田地震，其震級為4.8級。本文選取表2所示的三次具有代表性的地震記錄進行分析。圖3是三次地震中SE1順河向觀測通道的記錄。大壩強震觀測系統還定時采集結構的環境激勵振動。本文選擇四次環境振動監測數據進行分析。圖4是SE1強震儀的水平順河向的環境振動監測數據。地震記錄和環境激勵振動監測的采樣頻率為100Hz，記錄時長為140s至160s。

圖3 三次地震的SE1強震儀水平順河向強震記錄圖Fig.3 Strong earthquake record of SE1 strong motion instrument with three earthquakes along the river

圖4 四次環境振動的SE1強震儀水平順河向振動記錄圖Fig.4 Vibration record of SE1 strong motion instrument with four environmental vibrations along the river

表2 三次典型地震記錄

4 水口重力壩模態識別結果分析

4.1 頻率和阻尼識別結果分析

當采用IO類方法進行模態識別時，將大壩左岸自由場的SE7強震儀的順河、垂直、橫河三個通道的觀測數據作為模型輸入，19#壩段上的SE1-SE4四個強震儀9個通道的觀測數據作為模型輸出。圖5是基于水口水電站三次地震記錄計算的頻響函數圖。頻響函數計算時以SE7順河向為輸入。表3是基于前文所介紹的三次大地震，利用ERA-IO、ARX、SSI-IO三種不同的IO方法識別出來的自振頻率和阻尼比。

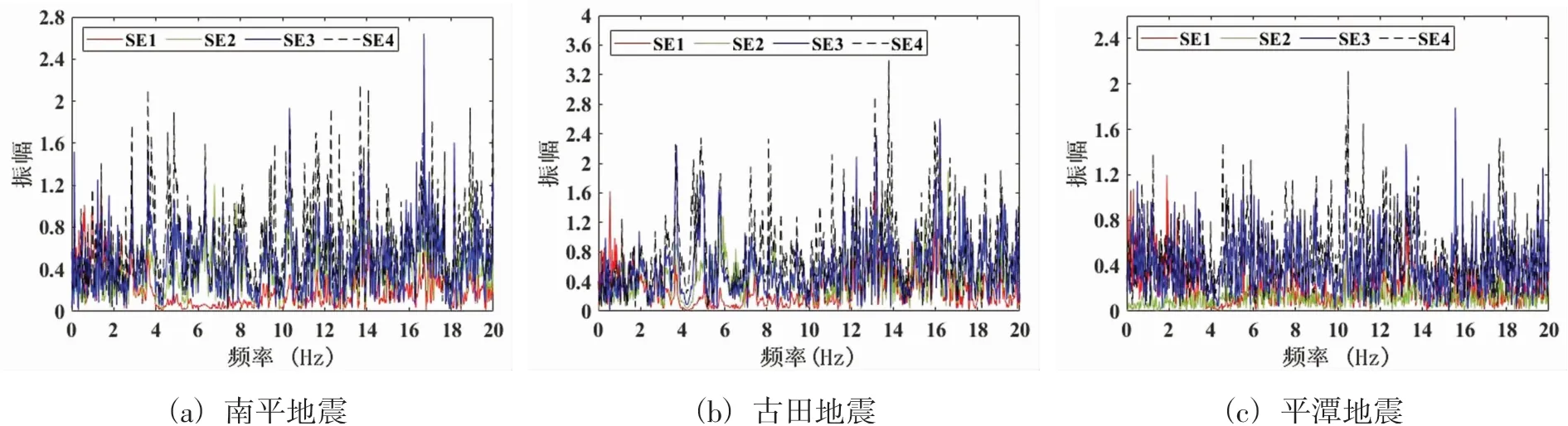
圖5 三次地震頻響函數圖Fig.5 Frequency response function of three earthquakes

表3 利用IO法對三次地震觀測數據識別頻率和阻尼的識別結果

（1）大壩基頻范圍為4.07~4.45Hz，利用前文擬合的經驗公式（13）得到的水口重力壩的基頻估值為4.62Hz，說明本工程重力基頻的識別結果符合一般工程經驗。

（2）利用不同識別方法得到的各階頻率大體相同，但有一定的差值。以南平地震為例，第一階頻率最大絕對值差值為0.06Hz，第二階為0.10Hz，第三階、第四階均有一種方法無法識別出對應頻率。這是因為相較于低階模態，高階模態在地震中的激勵響應要小很多，模態識別的結果不如低階。阻尼比的識別結果并不理想，以古田地震為例，第一階阻尼比最大絕對值差值為0.69%，第二階為5.13%，第三階為2.21%。阻尼比差值與模態階數之間并沒有顯著規律，需進一步研究阻尼比的識別問題。

（3）利用同一方法對不同地震激勵的識別結果不同。以SSI-IO的識別結果為例，南平地震識別出了前四階頻率，古田地震僅識別至第三階頻率，平潭地震僅識別出前兩階頻率。因為三次地震中南平地震的各通道加速度最大，激勵輸入能量最大，對于高階模態的激勵效果最好，可以識別出更多階模態。對比前兩階頻率的識別結果，南平地震識別頻率分別為4.13Hz和5.30Hz，為三次地震最低；古田地震和平潭地震識別頻率各有高低。因為相較于后兩個庫水位相近的地震，南平地震發生時庫水位最高，導致其識別的各階頻率較低。

采用OO類方法進行模態識別時，將19#壩段上的SE1-SE4四個強震儀9個通道的觀測數據作為模型輸出。圖6是兩個利用ERA-OO進行模態識別的穩態圖。表4是基于四次典型環境振動激勵監測數據，分別采用ERA-OO、FDD、SSI-OO三種不同的OO類方法識別出的結構自振頻率和阻尼比。由表4可知:

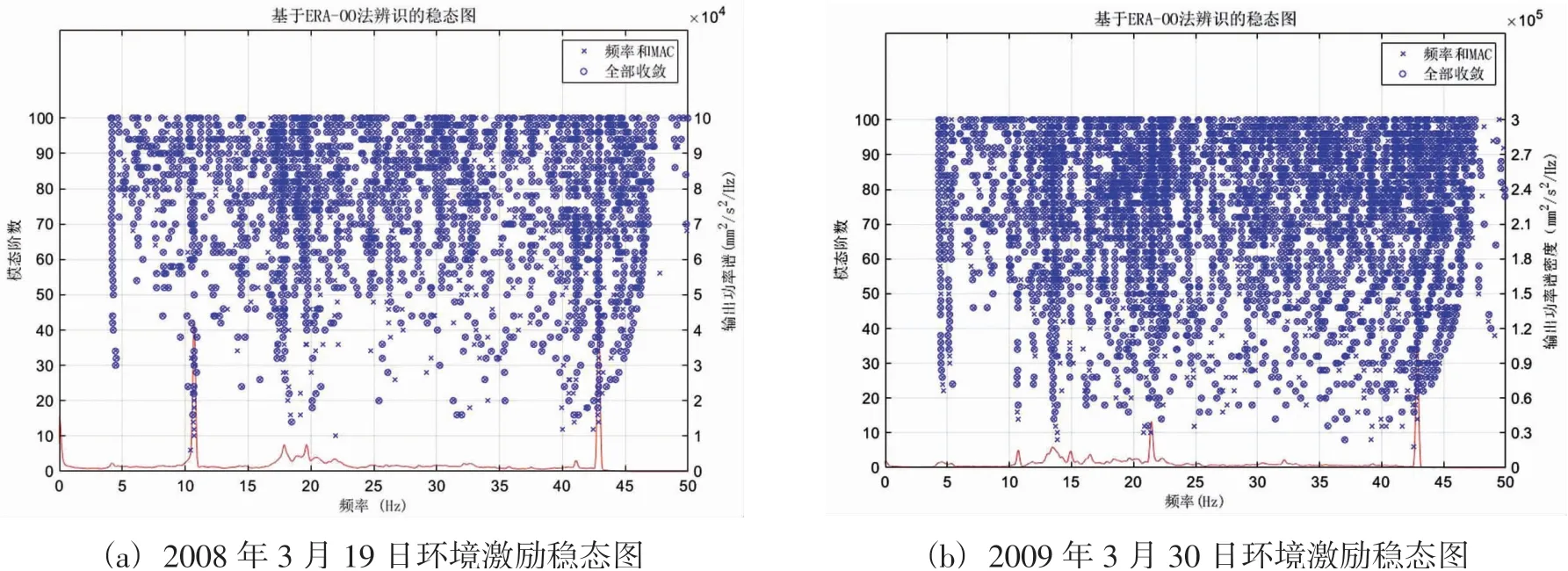
圖6 不同環境激勵采用ERA-OO方法識別的穩態圖Fig.6 Steady state diagram identified by ERA-OO method under different ambient excitation

表4 利用OO法對四次環境振動觀測數據識別頻率和阻尼的識別結果

（1）大壩基頻范圍在4.12~4.47Hz之間，與前文基于地震激勵的識別結果類似，基本符合經驗的范圍。

（2）以2009年3月23日環境振動為例，第一階頻率最大絕對值差值為0.03Hz，第二階為0.05Hz， 第三階為0.13Hz， 第四階為0.17Hz。隨著階數提升，不同方法的識別頻率差值逐漸變大，這也同樣驗證了前文高階模態識別難度高的結論。阻尼比識別結果仍舊不理想，不同方法識別的阻尼比差值均遠大于頻率。將表4利用OO法的識別結果與表3利用IO法的識別結果整體進行對比，OO法的識別結果更加完整，但是其對第四階頻率的識別結果絕對差值較大（0.64Hz）。

（3）選取發生在同一天的平潭地震和2009年3月23日環境振動的SSI識別結果進行對比。如圖6所示，兩者前兩階的識別結果十分接近，最大頻率差值僅為0.04Hz，基于環境激勵的低階識別結果與基于地震識別結果相近。

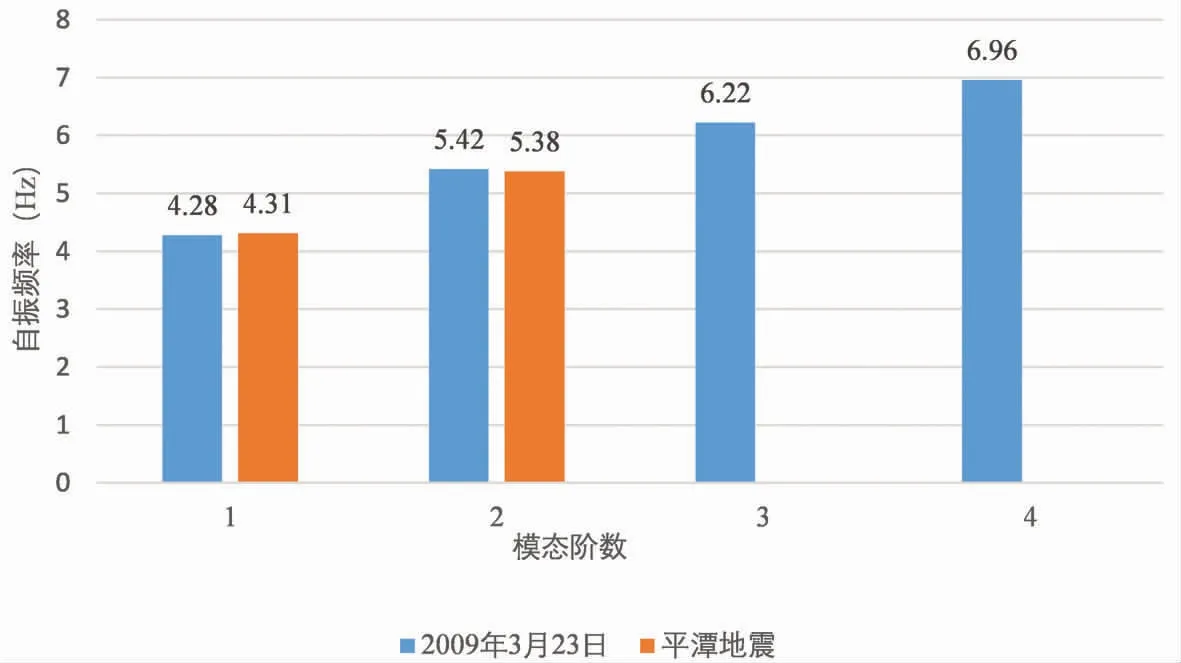
圖7 平潭地震和2009年3月23日環境振動SSI識別結果對比圖Fig.7 Comparison of SSI-OO identification results of Nanping earthquake and environmental vibration on March 23，2009

總而言之，利用OO法對環境振動進行系統識別雖然可以得到結構彈性狀態下的模態參數，且識別結果較為完整，但是由于環境振動相對于地震振幅較小，存在的白噪聲影響相對較大，利用不同方法的高階識別結果差距較大。但是就前兩階的識別結果而言，利用不同方法的環境激勵識別結果基本一致。相較于地震激勵信號，環境激勵信號顯然更易獲得，可以通過大量的環境振動激勵信號識別，得出可靠的結構模態參數，這是利用原型地震激勵進行系統識別所不具備的條件。

4.2 振型的識別結果分析

圖8 是南平、古田、平譚三次地震利用ARX、ERA-IO和SSI-IO三種方法識別的第一階振型計算的模態置信因子（MAC）。由圖8可以看出，不同方法計算的MAC值在0.65~0.99之間，說明不同方法識別的振型有一定的差異。

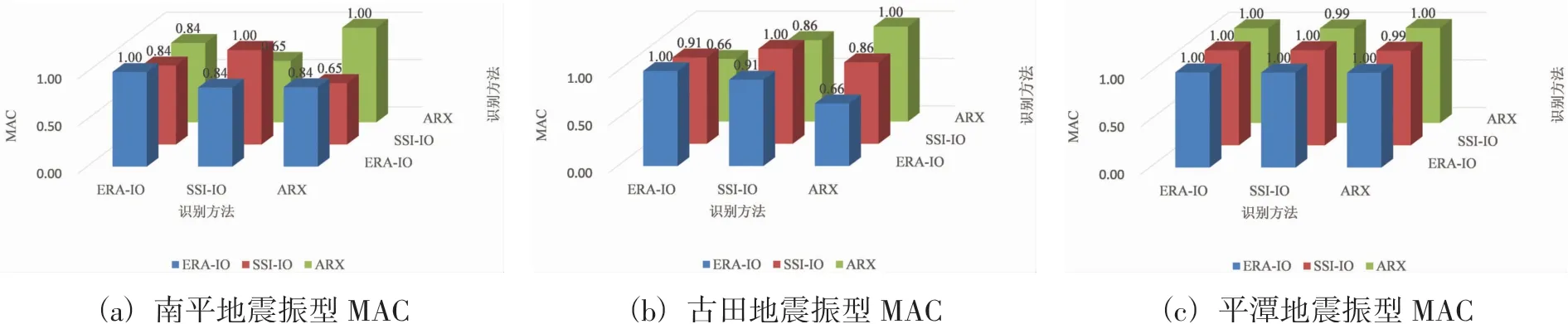
圖8 采用不同方法識別的結構第一階振型的對比Fig.8 Comparison of the first mode shapes of structures identified by different methods

5 結論

本文對不同的地震記錄和環境振動記錄采用了不同的識別方法，對水口重力壩的模態識別結果進行分析，主要結論如下:

（1）采用環境振動激勵和地震激勵的模態識別結果有一定差異。雖然環境激勵的識別結果有較高的準確度，但是由于環境振動振幅較小，包含頻率較少，對于高階的自振頻率激勵效果不佳。這給利用環境振動激勵進行模態識別得到準確的識別結果帶來了一定困難。

（2）即便是相同的激勵，采用不同識別方法，模態識別結果都有一定的差異。因此如何根據具體情況選用合適的識別方法是今后研究的重要問題。

（3）文中采用的各識別方法識別的阻尼比存在較大差距，結構阻尼比的識別仍是較大的問題。