基于張量分解的噪聲抑制算法研究
宋毅梁
(四川大學計算機學院,成都610065)
0 引言
高光譜圖像是一種被廣泛運用在植被勘探、地質檢測、農業、軍事、天氣等領域的成像手段。不同材質的物體其分子和原子的排列決定了其本質的特征,而當電磁波攝入到不同的物質上,其物質的分子、原子排列特征、震動等會讓物體呈現不同的光譜吸收與反射的特征。而高光譜成像便是運用這一特點,運用大量的窄波波段的電磁波(<10nm),得到一個帶有大量不同波段數據信息的三維數據塊。在空間圖像維的圖像與一般的圖像沒有分別,而對于光譜維來說,圖像的每一個像元都有大量的不同波段的光譜信息。
在日常采集高光譜圖像信息的過程中,因為采集時采集通道可能因為這個過程中產生的熱噪聲使得原本的圖像被噪聲污染,而高光譜圖像數據在有噪聲污染的情況下會給后續的數據分析帶來很大的障礙。因此去除這類加性噪聲會為之后的數據分析帶來便利。
傳統的噪聲抑制方法,把張量數據的二維圖像以光譜維展開成二維的矩陣,之后運用矩陣的低秩先驗的特點,對圖像進行PCA等降維去噪。而這種去噪方式并沒有考慮到圖像的光譜維之間的聯系,會損失掉不少的圖像結構信息。因此基于張量代數的去噪方式是當前高光譜圖像噪聲抑制的重點課題。
目前主要的基于張量代數的算法有Tucker分解和CP分解兩種方式。基于Tucker3的噪聲抑制方法包括低秩張量近似LRTA[1]、遺傳核張量分解[2],以及多維維納濾波[3]。基于CP分解的噪聲抑制方法有并行因子分析(PARAFAC)[4]和秩-1張量分解[5]。除此之外基于高階張量圖像數據的小波分解噪聲抑制方法因其良好的細節保留特性也被大量提出[6-8]。這些噪聲處理方式對于受到高斯白噪聲影響的HSI圖像的信號空間還原是比較高效的。但是在遇到完全丟失像素信息的椒鹽噪聲、死像素等則不能有效處理。而近年以來提出的魯棒性主成分分析(RPCA)[9],這種方法已經被驗證可以在傳統圖像上對稀疏噪聲進行有效的噪聲抑制還原原始信號。而這種方法的高階推廣也被人提出并且用在稀疏噪聲的HSI圖像的噪聲抑制上。TRPCA[10]用 || ||Z*張量的核范數TNN被用于描述張量的秩。除此之外還有基于TV全變差等方法的提出。本文針對目前已經出現的基于張量分解的噪聲抑制方法進行了分析和效果對比。
1 張量基本概念與分解模型
1.1 張量的基本概念
(1)張量的mode-n展開
張量的mode-n展開是把張量的第n個mode的纖維(fibers)作為展開矩陣的列向量然后把這些mode的纖維順序排列。一個張量X∈R I1xI2xI3的mode維展開為x(n)∈R I n xM n,其中Mn=I1X….I n-1XI n+1….I N。
(2)張量的mode-n乘積
張量X∈R I1X…XI N與矩陣U∈R JXI n的mode-n的乘積被表示為XxnU,實質上是張量的n-mode的纖維(fi?bers)與矩陣相乘。因此有公式:

(3)秩-1張量
秩-1張量表示N個矢量進行外積得到的張量,而外積之后的張量階數取決于外積矢量的個數,其形式為:

此為N階的秩-1張量。
1.2 張量分解模型
(1)Tucker分解
Tucker分解是奇異值分解(SVD)的高階推廣,一個三階張量的Tucker分解會把張量X∈R I1×I2×I3會被分解為一個核張量G∈R M×N×J和三個分別對應三個mode做乘積的系數矩陣A∈R I1×M、B∈R I2×N與C∈R I3×J。其分解的表示形式為:

此外對張量的mode積而言,對對應的mode做乘積相當于在這個mode上做投影。
(2)CP分解
CANDECOMP/PARAFAC分解(簡稱CP分解)這種分解會把張量分解為秩-1張量的和。而張量的CP-秩被表示為分解的秩-1張量的個數。

2 張量噪聲抑制算法
2.1 基于Tucker分解的LRTA算法
LRTA算法運用主成分分析(PCA)的思想擴展到高階的HIS三階張量圖像數據上,通過估計信號空間的維度在降維后還原原始圖像。令加性噪聲在對每個mode的投影中與信號空間分離以此在達到收斂條件之后得到估計信號的結果。
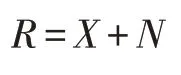
一般的高斯噪聲模型認為采集圖像所攜帶的噪聲是一種加性噪聲,而想要去除高斯白噪聲這樣的加性噪聲,重要的就是把采集到的數據投影在算法估計的信號空間上。在PCA里,這樣的投影工具是一個矩陣它把二維圖像數據降維投影得到最逼近原始信號的數據。而對于三階張量數據來說,對各個mode進行投影則是在各個mode上進行mode-n乘積。因此問題的關鍵在于得到每個mode對應的投影矩陣p(i)。估計的信號空間數據被表示為:

而每個mode對應的信號空間的投影需要先知道每個mode信號空間的維數K n,這些維數的確定依賴于張量Tucker-秩。(K1,…,K N)每個mode的秩被作為衡量Tucker分解的張量秩。而基于高階PCA思想的這種去噪方式所要處理的其實是如下的優化問題:

顯然求張量的秩是一個非凸的問題,因此要變為可求解的優化形式:
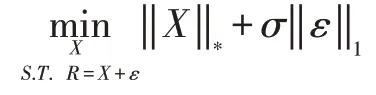
張量的核范數是張量沿每個mode展開之后求得的奇異值之和。而最小化核張量SNN則是滿足低秩先驗的條件。
LRTA算法描述:
(1)input:高光譜HSI張量數據R,以及被估計的投影空間(K1,…,K N)


2.2 基于CP分解的噪聲抑制算法
基于CP分解把張量分解為秩-1張量的想法,提出把張量分解為帶權值的秩-1張量。認為張量的信號空間是一組高度相關的秩-1張量組成的,噪聲則在光譜域的相關性較小。
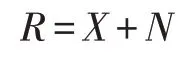
通過CP分解后得到的帶權值的秩-1張量:

其中M是采集信號R的CP分解所需要的秩-1張量的總個數,而αr則是每個秩-1張量所占信號空間表達的權值。要通過R求解未被噪聲污染的信號關鍵在于求解張量的秩。而與矩陣不同,張量的秩在目前還沒有明確的定義形式[11]。
不同于Tucker的各個mode上的秩表示張量的秩,而是分解后秩-1張量的個數被表示為了張量的秩序。又因為該方法認為噪聲以加性信號為前提而高斯白噪聲在信號空間里是并不相關的因此存在的權值很小,而信號空間因為在光譜空間上高度相關因此權值占得比重更大,得到的被估計的信號空間可以表示為:
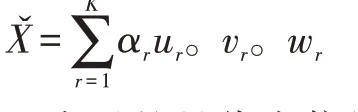
K表示的是代表信號空間的秩-1張量的個數,也是權值最大的K個秩-1張量。


而W、V同理可以根據上邊的方式迭代跟新,最終當這一次迭代減去上一次迭代的值滿足條件時就可以跳出得到估計的信號張量數據X?。
R1TD算法描述:
(1)input:高光譜HSI張量數據R,以及被估計的秩-1張量個數K,最大迭代數M
(2)循環t=1→M
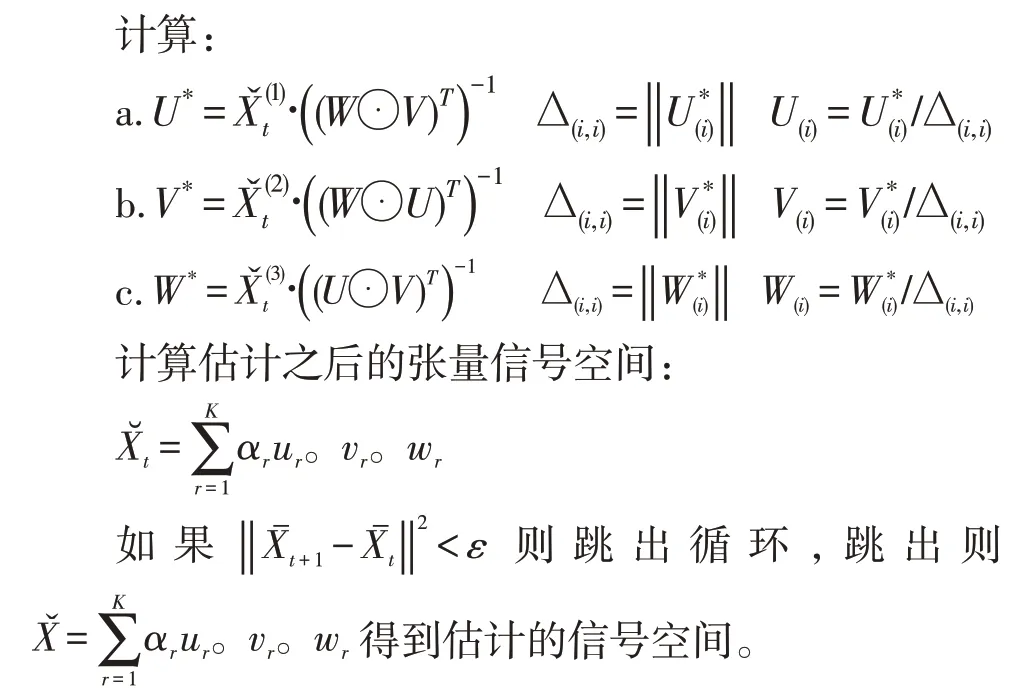
2.3 Tucker-秩與CP-秩的估計方法
(1)AIC赤池信息準則
AIC是一種優秀的模擬統計信息的一種標準[12],因為張量秩的定義不像矩陣一樣明確,因此AIC用于估計擬合各個mode上的統計信息,即Tucker-秩。

(2)CP分解秩-1張量的估計
秩-1張量定義的秩不能通過計算每個mode的統計信號擬合來直接得出。需要利用信噪比得到:
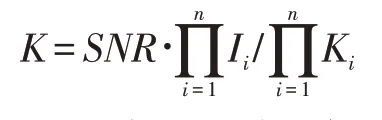
Ki是由AIC得到的每個mode對應的統計擬合SNR是張量的信噪比,而在輸入條件并不知道信號空間的時候,信噪比可以通過求統計算法的結果得到近似的評估。
(1)在張量中準備一個移動窗口,5×5、7×7等,計算部分圖像區域的方差,得到最小的方差,把這個方差作為噪聲的統計信息估計。
(2)求出信號統計信息的估計:

3 Tucker與CP的抑制效果對比
本節運用的HIS圖像數據為Washington DC Mal,Indian Pine高光譜圖像數據集合,對圖像添加加性的高斯白噪聲在不同波段的圖像分別應用LRTA和R1TD兩種基于張量分解的噪聲抑制方法進行去噪聲,通過對圖片細節與峰值信噪比PSNR等圖像效果指標進行評估對比。

圖1
圖片從左到右依次為(1)原始圖像211光譜波段(2)加入高斯白噪聲之后的211光譜段圖像(3)LRTA處理之后的211波段圖像PSNR為29.603(4)R1TD處理之后的211波段圖像PSNR為33.011
圖像在進行了張量的低秩分解處理之后噪聲得到抑制,不過兩種方法都基于低秩的去噪方法因此在細節上并沒有得到很好的保留。
4 結語
本文對主流的兩種張量分解的噪聲抑制方法進行了闡述并分析了其工作原理,并且利用Washington DC Mal,Indian Pine高光譜數據集進行了仿真。利用PSNR等方法對噪聲抑制之后的光譜波段進行了對比。通過實驗與對比之后發現在進行這兩種方法之后,去噪過程實際上是在降低數據的維度,不可避免地會造成細節的丟失因此未來的工作可以如何對細節盡可能地保留等課題上。

