基于KNN算法的船舶噸級判別研究
陳冬 袁媛


摘 要:針對航運大數據應用中船舶噸級數據難以獲取的情況,本文提出了一種基于K最近鄰(K-Nearest Neighbor,KNN)算法的船舶噸級判別模型。該模型考慮了船舶類型、船長、型寬、型深等參數的影響,以常年在江蘇沿江、沿海運行的船舶為例,選取1萬余條船舶數據進行訓練和驗證。結果表明,該模型在船舶噸級判別上具有較好的準確性,能夠應用于實際航運數據分析。
關鍵詞:船舶特征;判別模型;K近鄰
中圖分類號:U674.13? ? ? ? ?文獻標識碼:A? ? ? ? ? ? 文章編號:1006—7973(2021)05-0104-02
1概述
船舶屬性數據是非常重要的基礎數據,包括船舶身份(IMO、MMSI、船名)、船舶類型、船舶尺度(船舶長度、船舶型寬、船舶型深、滿載吃水)、船舶噸級(船舶總噸、船舶凈噸、船舶載重噸)等內容。在航運大數據應用中,船舶屬性信息與船舶動態信息相結合,能夠為航運各領域發展決策提供支撐,如將船舶屬性信息中的船舶噸級與船舶AIS數據相結合,能夠估算港口在某段時間內的吞吐量。但在航運數據的實際應用過程中,由于航運數據開放共享格局尚未形成,研究人員較難獲得全部船舶屬性數據,尤其是船舶屬性數據中的船舶噸級信息,如AIS數據的船舶靜態信息僅僅包括船舶身份、船舶長度、船舶型深、船舶類型等內容,缺少船舶噸級等內容,使航運大數據的應用缺少關鍵基礎數據支撐。
傳統的船舶噸級推算主要是利用船舶長度通過曲線估計來計算船舶噸位。傳統方法需針對不同的船型選擇不同的曲線(二次曲線、立方曲線、S曲線、冪函數等)進行擬合,建模過程繁雜,使用較為不便[1]。針對船舶噸級信息難以獲得以及傳統估算方法使用不便的問題,本文探索了大數據機器學習方法,提出了基于KNN算法的船舶噸級判別模型。
2 KNN算法
2.1 KNN算法原理
KNN(K-Nearest Neighbor)算法即K最鄰近法,是機器學習算法中最常用的分類算法之一,KNN算法主要應用領域是對未知事物的判別,即判別位置事物屬于哪一類[2-3]。
算法模型首先對給定的一個訓練數據集T進行訓練。其中,xi為實例的特征向量,yi為實例的類別。
輸出過程中,根據給定的距離度量,在訓練集T中找出與x最鄰近的k個點,涵蓋這k個點的x的鄰域為Nk(x);在Nk(x)中根據分類規則決定x的類別y。
KNN算法模型由距離度量、k值的選擇和分類決策規則決定。
2.2 KNN算法實現流程與評價指標
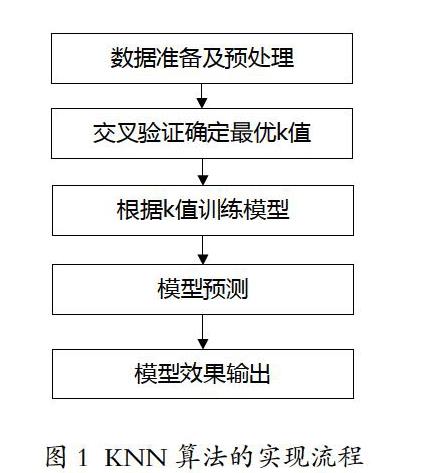
相比傳統的依據船舶長度的曲線估計方法,本次基于KNN的船舶噸級判別模型選取了更多的特征向量并采用不同組合進行建模,模型1選取“船舶總長、型寬、船舶類型”為特征向量,模型2選取“船舶總長、型寬、型深、船舶類型”為特征向量。算法的實現流程如圖1所示。
為驗證模型的可靠性,模型采用決定系數(R2)作為精度評價指標,R2代表目標向量的變化中有多少能通過模型進行解釋,具體計算公式為:
式中,是樣本i的真實值,是樣本的預測值,是目標向量的平均值, R2得分越接近1,代表模型的性能越好。
3 船舶噸級判別模型
3.1 基礎數據
本文數據采用常年在江蘇沿江、沿海運行的約1.5萬艘船舶屬性數據,數據內容包括船名、MMSI號、IMO號、總長、型寬、型深、總噸、凈噸、載重噸、船籍港、經營人等信息,具體數據示例如表1。
沿江、沿海運行的船舶種類較多,主要船舶種類包括散貨船、石油化學品船、雜貨船等。本次根據海港總體設計規范,以船舶載重噸計算了散貨船、雜貨船、石油化學品船、集裝箱船等貨運船舶的船舶噸級。船舶主要類型及等級分布如圖2所示。
3.2 特征數據處理
船舶屬性數據處理步驟包括:
(1)數據清理。對船舶類型、載重噸等關鍵屬性缺失以及船舶類型樣本較少的船舶數據進行刪除處理,最終得到9490條船舶的屬性信息。
(2)數據特征量化。特征向量中的船舶類型和目標向量中的船舶噸級為非數值類型,需將其量化為數值,以實現距離計算。
(3)數據抽樣。訓練集與測試集按照9:1的比例進行數據抽樣,最終得到8541條訓練樣本和949條測試樣本。
3.3 模型參數標定
KNN模型的預測效果依賴于不同鄰近數K值的選定,K值太大容易引起欠擬合,太小則容易過擬合。本文通過交叉驗證確定最優k值,從圖3可以看出,K=3時,交叉驗證得分R2最高,為0.96,因此取K=3標定本次船舶噸級判別模型。
3.4 模型預測結果分析
用上述建立的KNN船舶噸級判別模型對測試集進行測試,從圖4對測試集的測試結果可以看出,兩種模型的預測值與真實值基本吻合,模型決定系數R2均大于0.9,準確性較好,其中選用“船舶總長、型寬、船舶類型”作為特征向量的模型1具有更好的測試效果。
4分析與結論
KNN方法較為適合類域交叉的待分樣本集的類別判別,本文基于KNN算法,以船舶總長、型寬、型深、船舶類型為特征向量,創新性地提出了船舶噸級判別模型,計算的結果與實際情況基本吻合,具有較好的準確性;同時,相比于傳統方法,本次提出的算法適用于不同尺度及類型的船舶噸級判別,應用更為便捷,能夠更好地為航運大數據研究提供基礎數據支撐。
參考文獻:
[1]朱連江.內河船舶交通量換算系數研究[D].大連:大連海事大學,2019.
[2]周志華.機器學習[M].北京:清華大學出版社,2016.
[3]霍豪,沈金星.基于KNN算法的公交到站時間預測[J].交通運輸工程與信息學報,2020,12(18):76-102.

