基于模擬退火算法組合優化問題的求解

高嘉 任亞明

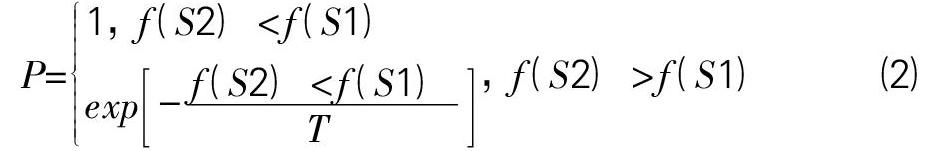
【關鍵詞】組合優化問題;模擬退火;分支界定

【中圖分類號】O221.4 【文獻標識碼】A 【文章編號】1674-0688（2021）05-0066-03

0 引言

在優化領域中，根據變量性質的不同大體可以分為兩類：一類是包含連續變量的優化問題;另一類是包含整數變量的優化問題（也可稱之為組合優化問題）。組合優化問題的目標是從組合問題的可行解集中求出最優解，組合優化往往涉及排序、分類等問題，它是優化領域的一個重要分支。

在求解組合優化問題中，人們首先想到的是取整的方法，即互聯組合優化問題變量必須為整數的約束條件，按照連續變量的優化問題對其進行求解，對于得到的結果按照某種方法取整。該方法簡單，但是所得到的結果往往會違背優化問題的約束條件或者得到次優的結果。在取整的基礎上，分支界定方法被提出，分支界定方法的本質也是按照連續變量的優化問題對其進行求解，不過在每次得到的結果不滿足整數約束時，并不是進行簡單的取整操作，而是通過縮小變量可行域的方法，逐步逼近問題的最優解。分支界定方法可以有效處理組合優化問題，但是其每次縮小可行域就要進行一次連續優化問題的求解[1]，因此計算量大。同時，由于采取連續變量的優化問題對其進行求解，對于所求解的數學問題有這嚴格的數學要求，例如函數必須連續且必須為凸，這樣才可以保證所求的解為問題的全局最優解，如果是多極值問題，無法保證結果為問題的全局最優解，解的狀態與問題的初始值密切相關，而初始值一般是隨機給定，因此分支界定方法的使用受到較多的約束與限制。

另一種求解組合優化問題的方法為智能化方法。常見的智能化方法有粒子群算法[2]、遺傳算法[3]、模擬退火算法[4]等。粒子群算法根據其迭代規則，如果變量為整數變量，需要在其迭代規則的基礎上進行進一步討論。遺傳算法和模擬退火算法其初始變量隨機生成，可以直接轉化為相關的整數，不需要做額外的變化。也就是說，遺傳算法和模擬退火算法都可以求解組合優化問題。遺傳算法與模擬退火算法相對比，遺傳算法需要選擇、交叉、變異，而模擬退火算法僅需要生成新的解，采取Metropolis準則與原解進行比較并進行相應的跟新操作。模擬退火算法迭代過程簡單，容易實現，因此本文采取模擬退火算法求解組合優化問題。

1 模擬退火算法的基本原理及編程實現

模擬退火算法通過觀察自然科學中固體退火過程類推而來，最早的思想是由N. Metropolis等人于1953年提出[5]。我們首先給出模擬退火算法的具體迭代步驟，然后逐條對其進行相應的解釋。

模擬退火算法的具體迭代步驟如下。

（1）設置模擬退火算法初始溫度T，降溫速率q，結束溫度Tend，Metropolis準則鏈長L。

（2）隨機生成組合優化問題的隨機初始解S1。

（3）將S1帶入組合優化問題的目標函數，求解目標函數值f? ?1。

（4）設置K=0。

（5）隨機生成新的組合優化問題的解S2;將S2帶入組合優化問題的目標函數，求解目標函數值f? ? 2。

（6）Metropolis準則，比較f? ?1和f? ?2更新S1。

（7）更新k=k+1;假如k

（8）更新溫度T=T*q，假如T<Tend，則停止迭代輸出結果;否則轉步驟（4）。

1.1 隨機生成組合優化問題的解的隨機生成

組合優化問題的隨機解生成代碼如下所示。

S1=round（LB+（UB-LB）*rand（1，N））? （1）

公式（1）中，S1為隨機生成組合優化問題的隨機解，LB和UB分別代表與預先給定的變量的下限和上限向量，rand為Matlab函數，表示生成0～1的均勻分布隨機數。round（）為Matlab函數，表示按照指定的小數位數進行四舍五入運算的結果，通過round操作可以保證組合優化問題的初始解為整數，而且是在給出的上下限范圍之內。

1.2 模擬退火算法的Metropolis準則

Metropolis準則的制定在于以一定的概率跳出當前的最優解，即以一定的概率接收新的解，即使該新解目標函數評價低于已經存在的最優解，其目的是跳出局部最優解，使得算法具有全局搜索的能力，這也是模擬退火算法最為核心的概念[6]。

S1表示當前解，其對應的目標函數值為f? ?（S1）;S2表示新生成的解，其對應的目標函數值為f? ?（S2）。組合優化問題的解由S1變為S2的接受概率P：

P=1，f （S2）f （S1） （2）

根據公式（2）的描述可知，當f? ?（S2）f? （S1）時模擬退火算法不會立刻將新生成的解S2拋棄，其實進行相應的概率操作，首先利用均勻分布函數生成一個0～1的服從均勻分布概率的隨機數，然后將這個隨機數和e^（-（f （S2）-f （S1））/T）相比較，假如生成的隨機數小于e^（-（f （S2）-f （S1））/T）則接受組合優化問題的解由S1變為S2，否則拋棄生成的新解S2。具體的偽代碼如下所示。

隨機生成新解S2;

? S1評價指標=以S1為變量帶入目標函數，返回的目標函數值;

? S2評價指標=以S2為變量帶入目標函數，返回的? 目標函數值;

評價指標差=S2評價指標-S1評價指標

if評價指標差<0

S1=S2;

S1評價指標=S2評價指標;

else

if exp（-dC/溫度）>0-1之間的均勻隨機數

S1=S2;

S1評價指標=S2評價指標;

end

end

通過對Metropolis準則的分析我們發現，只有當f （S2）>f （S1）時，Metropolis準則才會以e^（-（f （S2）-f （S1））/T）的概率接受新解，此時-（f （S2）-f （S1））/T的值一定為負，因此e^（-（f （S2）-f （S1））/T）的值一定是0～1的開區間。同時我們發現e^（-（f （S2）-f （S1））/T）的大小還與當前時刻溫度T有關，根據模擬退火算法的具體迭代步驟可知，隨著迭代次數的增加，溫度T是逐漸變小，我們假設f （S2）-f （S1）大小不變的情況下，隨著溫度T變小e^（-（f （S2）-f （S1））/T）的值也在不斷變小趨近于0。因此，在迭代的初期，模擬退火算法以較高的概率跳出當前最優解，其目的是保證算法的全局收斂能力，在迭代的末期，模擬退火算法以較低的概率跳出當前最優解，其目的是在最優解附件搜索提高算法結果的精度。

2 仿真

2.1 仿真算例

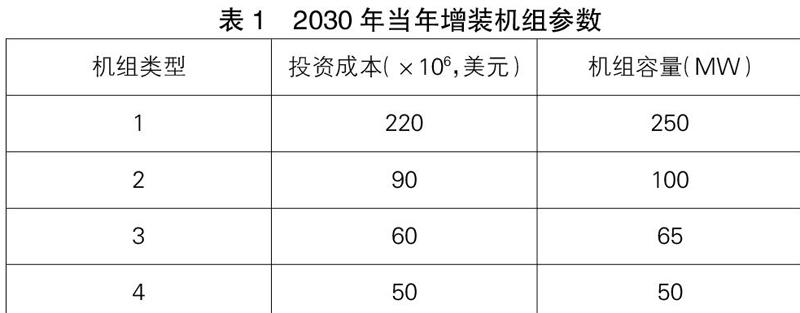
在這一節中，我們采取的算例是來自2019年“電工杯數學建模大賽”A題，電源規劃第二問。具體的算例描述如下：IEEE-RTS單階段電源擴展規劃（目標函數只考慮機組投資費用），IEEE-RTS系統由32臺發電機組構成，總裝機容量為3 405 MW，峰值負荷為2 850 MW。以2019年為基準年，假設2030年系統峰值負荷增長30%，規劃2030年當年增裝機組的類型和數量（見表1）。

根據問題的描述，我們建立如下的數學模型：

minF=x1*220+x2*90+x3*60+x4*50

s.t. 5≥x1≥0，x1≥為整數

11≥x2≥0，x2≥為整數 （3）

17≥x3≥0，x3≥為整數

21≥x4≥0，x4≥為整數

x1*250+x2*100+x3*65+x4*50+3 405≥4 446

其中，變量x1、x2、x3和x4分別代表表2中機組類型1、2、3和4的新建機組數量。當然根據工程建設的要求，我們需要以最小的工程造價為目標函數。

2.2 仿真分析

設置模擬退火算法初始溫度T=150，降溫速率q=0.9，結束溫度Tend=1e-06，Metropolis準則鏈長L=1 000，運行模擬退火算法得到結果：[x1，x2，x3，x4]=[3 3 0 0]，目標函數為930，其目標函數變化曲線如圖1所示。

為了驗證模擬退火算法得到結果的準確性，我們采取分支界定算法對問題（3）進行求解，得到的變量的解和最優目標函數值為[x1，x2，x3，x4]=[3 1 3 0]，目標函數為930。很明顯，模擬退火算法和分支界定算法得到的最優目標函數均為930，但是兩者得到的解不相同。這說明了組合優化問題（3）有多個解。為了求解組合優化問題（3）的解，我們定義矩陣RESULT保存迭代過程中最優解及其函數值的信息，前4列保存解，第5列保存該解所對應的目標函數，矩陣RESULT的初始值=[迭代步驟（2）隨機生成的初始解S1，S1對應的目標函數]，對模擬退火算法每次迭代的Metropolis準則進行改進，具體的偽代碼如下所示。

隨機生成新解S2;

S1評價指標=以S1為變量帶入目標函數，返回的? 目標函數值;

S2評價指標=以S2為變量帶入目標函數，返回的? 目標函數值;

評價指標差= S2評價指標- S1評價指標

if評價指標差<0

S1=S2;

S1評價指標=S2評價指標;

end

if評價指標差>0

if exp（-dC/溫度）>0-1之間的均勻隨機數

S1=S2;

S1評價指標=S2評價指標;

end

end

if評價指標差==0

flag=0;

if 矩陣RESULT第一行最后一列>S2評價指標

矩陣RESULT置為空矩陣;

RESULT=[S2，S2評價指標];

end

if矩陣RESULT第一行最后一列==S2評價指標

for i=1：矩陣RESULT的行數

if矩陣RESULT第i行前4列與S2相同

置變量flag為1，跳出當前循環;

end

end

if flag==0

RESULT=[RESULT;[S2，S2評價指標]];

end

end

end

現在根據我們改進過的模擬退火算法，再次執行程序，得到結果見表2。在表2中，我們得到了3組最優解，其最優目標函數值均為930。說明這3組解均為原問題（3）的最優解。

3 總結

本文利用模擬退火算法求解組合優化問題，仿真結果證明了模擬退火算法的有效性，通過進一步分析與比較仿真結果與分支界定算法仿真結果，發現仿真算例存在多個極值點，我們在原有基礎上進一步改進模擬退火算法的Metropolis準則，同時輸出組合優化調度問題的多個極值點。

參 考 文 獻

[1]龔純，王正林.精通MATLAB最優化計算[M].北京：電子工業出版社，2009.

[2]吳辰斌，李海明，劉棟，等.一種改進型粒子群優化算法在電力系統經濟負荷分配中的應用[J].電力系統保護與控制，2016（10）：44-48.

[3]何大闊，王福利，毛志忠.基于改進遺傳算法的電力系統經濟負荷分配[J].控制與決策，2007（2）：230-232.

[4]王述紅，朱寶強，王鵬宇.模擬退火聚類算法在結構面產狀分組中的應用[J].東北大學學報（自然科學版），2020，41（9）：1328-1333.

[5]鄭小虎，鮑勁松，馬清文，等.基于模擬退火遺傳算法的紡紗車間調度系統[J].紡織學報，2020，41（6）：36-41.

[6]陳科勝，鮮思東，郭鵬.求解旅行商問題的自適應升溫模擬退火算法[J].控制理論與應用，2021，38（2）：245-

254.