考慮樁
——土相互作用的多跨連續梁橋梁自振響應分析

周小東 鄒慧娜

1.江西省吉安市公路局吉安分局，中國·江西 吉安 343100

2.江西方興科技有限公司，中國·江西 南昌 330025

1 引言

橋梁的動力特性是其結構自身的屬性，反映了結構在動力作用下的反應特性[1]，分析和認識長跨徑公路橋梁結構的自振特性及動力響應對橋梁的抗震設計具有重要的意義。自19世紀中期以來，中國對橋梁振動問題已進行了大量研究[2]。

張巍[3]以某新建三跨預應力混凝土變截面連續箱梁橋為背景，通過建立有限元仿真計算模型和動載試驗現場測試相結合的方法對橋跨進行自振特性和動力響應分析，得出橋面平整度和車輛緊急制動對橋跨的沖擊效應影響較大。

王巖[4]通過建立主跨220m連續剛構橋與矮塔斜拉橋地震動力分析模型，分析并比較了地震荷載作用對不同橋型的自振周期及對橋墩底部的內力影響。

曾勇、鐘華棟等[5]利用MIDAS Civil建立不同腹板曲線連續剛構橋計算模型，通過改變樁基邊界約束和激勵角度，對比分析其自振特性和抗震性能變化規律。

苗戰濤[6]以朝陽溝水庫特大橋為研究對象，建立全橋空間力學有限元模型，通過計算多箱室波形鋼腹板箱梁、傳統砼腹板箱梁的自振頻率和振型，對比分析了兩種截面形式的動力特性。

馬馳、劉世忠等[7]通過考慮剪滯剪切變形效應和頂底板的不同材料屬性，采用等效剛度法對傳統波形鋼腹板（簡稱CSW）和CSWSB組合箱梁的動力特性進行對比，分析得到CSW組合箱梁的自振頻率均小于CSWSB組合箱梁的自振頻率，振型模態完全吻合，振動趨勢一致。

成凱、葉錫鈞等[8]通過有限元分析軟件MIDAS對某大跨度異形人行拱橋動力特性進行分析，分析了拱橋的自振頻率影響因素，發現拱肋的彈性模量和重度對拱橋的自振頻率影響最大。

肖光清[9]采用有限元軟件Midas Civil建立了考慮樁土效應和不考慮樁土效應的有限元模型，對比分析了樁土效應對結構動力特性的影響。

論文運用SAP2000軟件，建立某實際預應力鋼筋混凝土連續箱梁橋的有限元模型，采用彈簧單元模擬實際的樁—土相互作用效應，根據“m”法確定彈簧剛度，對比分析不同結構參數下多跨徑公路橋梁的自振響應特性，為認識該類多跨連續梁橋的動力特性及抗震分析提供基礎。

2 工程概況

論文以某多跨連續梁橋為背景，共3聯，其跨徑布置為（4×30＋28＋2×40＋28＋3×30）m的預應力鋼筋混凝土連續箱梁橋。第一、三聯橋梁上部結構為C55預應力鋼筋混凝土箱梁結構，下部結構為雙柱式橋墩，為C30混凝土結構，橋墩處采用板式橡膠支座，橋臺及過渡墩也為C30混凝土結構，橋臺及過渡墩處采用滑板支座。第二聯上部結構為現澆C55鋼筋混凝土箱梁，采用墩梁固結形式，在過渡墩處設置摩擦擺支座。橋型布置如圖1所示。

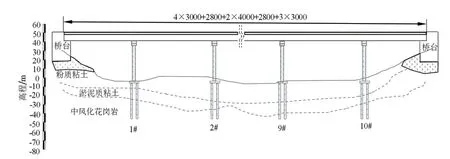
圖1 橋型布置圖（單位：cm）

3 考慮樁土相互作用的多跨橋梁有限元建模

為分析樁—土效應對長跨徑公路橋梁的自振響應的影響，根據該橋的設計方案，采用SAP2000有限元程序，建立三維有限元動力計算模型進行自振動力特性分析，計算模型以順橋向為X軸，橫橋向為Y軸，豎橋向為Z軸。全橋結構均采用空間梁單元模擬，第一、三聯橋梁的墩梁連接處為板式橡膠支座，采用彈簧單元模擬，其剛度根據中國公路橋梁板式橡膠支座規范[10]，取剛度7.9×107N/m，第二聯橋梁的墩梁連接方式為墩梁固結，采用剛性連接模擬，過渡墩處按為摩擦擺支座，按照實際剛度情況采用一般連接模擬。

樁與土相互作用受力復雜，若將土體對樁的作用力視為線彈性問題，而不考慮其非彈性問題，則可用土彈簧的剛度來模擬土體對樁的作用力。土彈簧剛度系數可由《公路橋涵地基與基礎設計規范》中的“m”法計算獲得[11]。第n層的土體彈簧剛度系數計算式如下：

式中：an為第n層土的厚度，b1為樁的計算寬度，mn為第n層土的比例系數，hn為第n層土的中心到地面的距離。土彈簧的豎向剛度系數通常將其簡化處理，近似為樁的豎向承載力除以豎向相對位移。

利用“m”法建立考慮樁土效應的有限元模型：首先，需要將樁基周圍的土體按實際情況進行分層；其次，根據土體情況選取合適的樁基節點位置；最后，通過計算每個節點位置的土彈簧水平剛度系數，用以施加邊界條件。全橋共計3070個節點，3040個梁單元，該橋的動力計算有限元模型如圖2所示。

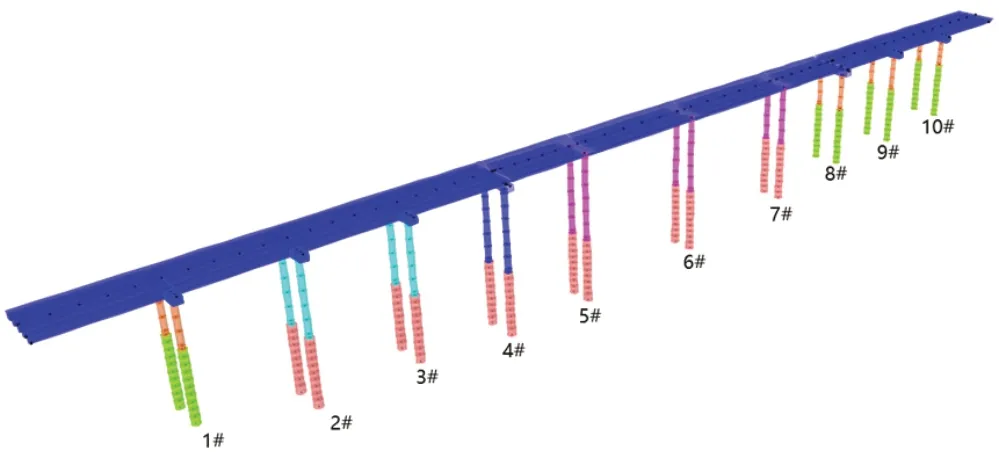
圖2 橋梁有限元計算模型

分析和認識橋梁的振動特性是進行橋梁抗震性能分析的基礎，橋梁結構的振動特性主要取決于它的各階自振頻率和主振型。在實際橋梁結構中阻尼對自振頻率和自振周期計算影響很小，通常忽略不計，因此橋梁的振動方程可簡化為：

式（2）具有非零解的條件為：

即（3）式的特征方程為：

4 考慮樁—土相互作用的多跨橋梁自振響應結果分析

論文使用Ritz向量法對該橋的動力計算有限元模型的前90階模態進行分析，并給出了前5階模態振型圖示，如圖3～圖7所示。

圖3 第1階振型圖

圖4 第2階振型圖

圖5 第3階振型圖

圖6 第4階振型圖

圖7 第5階振型圖

由圖3～圖7的橋梁前五階模態振型圖分析可知，在考慮樁—土相互作用效應下，橋梁第一階模態振型主要為第一聯的振動，體現在墩柱出現縱向（X向）彎曲，橋梁第二階模態振型主要為第三聯主梁的面內轉動，橋梁第三階模態振型為第一聯的主梁面內轉動，橋梁第四階模態振型為第三聯縱向彎曲振動，橋梁第五階模態振型為第二聯縱向彎曲振動。

為對比不同墩高、樁土相互作用等對多跨連續梁橋自振特性的影響，建立了4種對比工況。工況1為橋梁初始設計；工況2為在工況1的基礎上將所有橋墩墩高減少5m；工況3為在工況1的基礎上將所有橋墩墩高增加5m；工況4為在工況1的基礎上不考慮樁土相互作用影響，直接在墩底固結處理。取橋梁的前10周期進行對比，如表1所示。

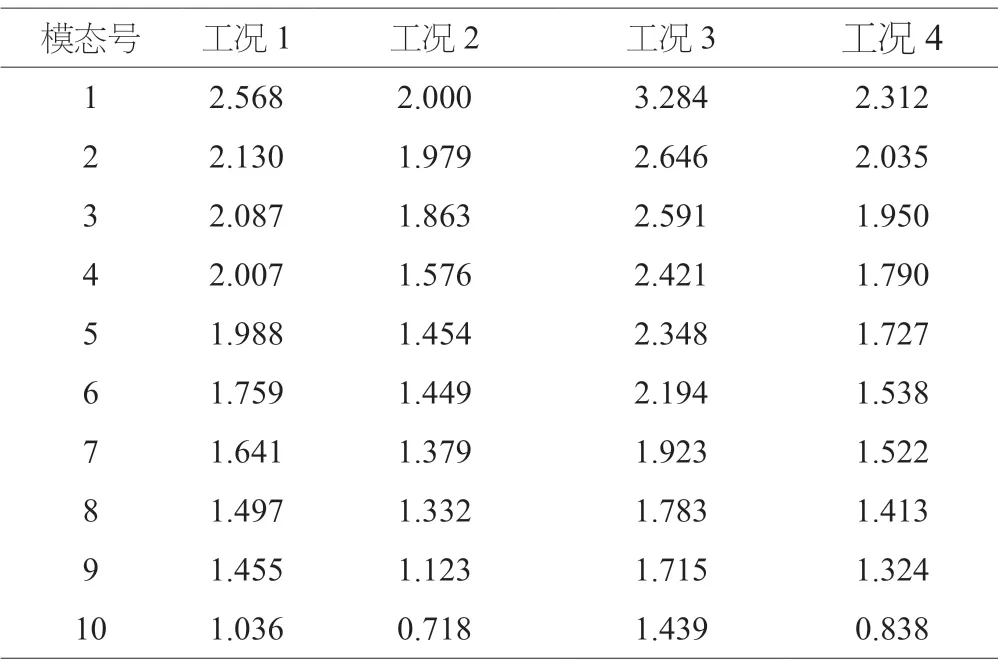
表1 結構前10階周期（S）

由表格1數據分析可知，結構幾何參數對多跨連續梁橋自振特性影響較大，隨著墩高增加，結構基本周期明顯增加，工況3基本周期較工況2增加了64.2%。其中，樁土相互作用對結構影響也較大，不考慮樁土相互作用的工況4結構自振周期要較考慮樁土相互作用的工況1小，其中基本周期要小10%，說明考慮樁土相互作用后，結構變柔，延長結構基本周期。

5 結語

論文通過建立某山區多跨連續梁橋三維有限元模型，分析了多跨公路橋梁的自振響應特性。得出如下結論：

第一，考慮樁土效應對橋梁結構的振型變化影響不大，但對其自振周期影響較大。因此，對長跨連續梁橋進行抗震分析時，應考慮樁土相互作用。

第二，對于多跨連續梁橋，墩高對結構自振特性影響較大。隨著墩高增加，結構基本周期明顯增加。