四足機器人跳躍控制規(guī)劃及仿真分析*

任坤照，田春霖，陳 帥，鄭 達，劉 巖

（1.西安交通大學(xué) 電氣工程學(xué)院，陜西 西安710000；2.西安交通大學(xué) 電信學(xué)部，陜西 西安710000；3.西安交通大學(xué) 機械學(xué)院，陜西 西安710000）

由于四足仿生機器人具有高機動性，負載和適應(yīng)能力強，可運用于物資運輸、搶險救援等方面，因而具有廣闊的應(yīng)用前景。

四足機器人的性能主要取決于對復(fù)雜環(huán)境的適應(yīng)能力，實現(xiàn)不同步態(tài)的規(guī)劃最為關(guān)鍵。目前，國內(nèi)外對四足機器人的Walk（慢步）、Trot（快步）等一般步態(tài)的研究都較為成熟，如Hiroshi Kimura等提出了基于各種復(fù)雜環(huán)境下的Walk步態(tài)的閉環(huán)控制系統(tǒng)[1]，李川等基于足端軌跡及CPG（Central Pattern Generators）網(wǎng)絡(luò)對兩種步態(tài)展開了研究[2-3]。但對于四足機器人的跳躍步態(tài)的研究較少，跳躍規(guī)劃的理論仍需完善，在機械結(jié)構(gòu)、運動過程中姿態(tài)調(diào)整也有待進一步改進，對其運動學(xué)、動力學(xué)的研究成為熱點。在實際場景中，跳躍步態(tài)可以跨越障礙物，適應(yīng)各種復(fù)雜地表，應(yīng)用廣泛，極大增強了四足機器人的運動性能。

本文著重對四足機器人的跳躍步態(tài)進行控制規(guī)劃并通過搭建仿真平臺進行驗證。根據(jù)足端是否觸地分階段采取利用幾何解析法進行軌跡規(guī)劃。利用D-H法建立機身質(zhì)心與各關(guān)節(jié)的坐標系，并基于正逆運動學(xué)對跳躍步態(tài)進行分析，求解出各階段關(guān)節(jié)角度函數(shù)。同時，根據(jù)Lagrange法以及D'Alembert's原理對跳躍過程進行動力學(xué)分析，得到關(guān)節(jié)電機的力矩驅(qū)動函數(shù)。

通過SolidWork軟件建立了全肘式四足機器人的結(jié)構(gòu)模型，使用ADAMS和MATLAB軟件對物理樣機進行運動學(xué)聯(lián)動仿真，驗證了跳躍控制規(guī)劃的有效性。

1 跳躍運動建模

四足機器人的設(shè)計模型如圖1所示。在跳躍過程中，只研究正中面上的運動特征，對冠狀面不做考慮。同時，由于在跳躍過程中前（后）兩腿的運動狀態(tài)相同，因此，可把四足機器人視為一維平面的多剛體系統(tǒng)。根據(jù)足底是否觸地，將跳躍過程分為起跳相、騰空相和著地相。在足端騰空時機器人與地面不存在約束限制，即機身不受外部作用力與力矩。

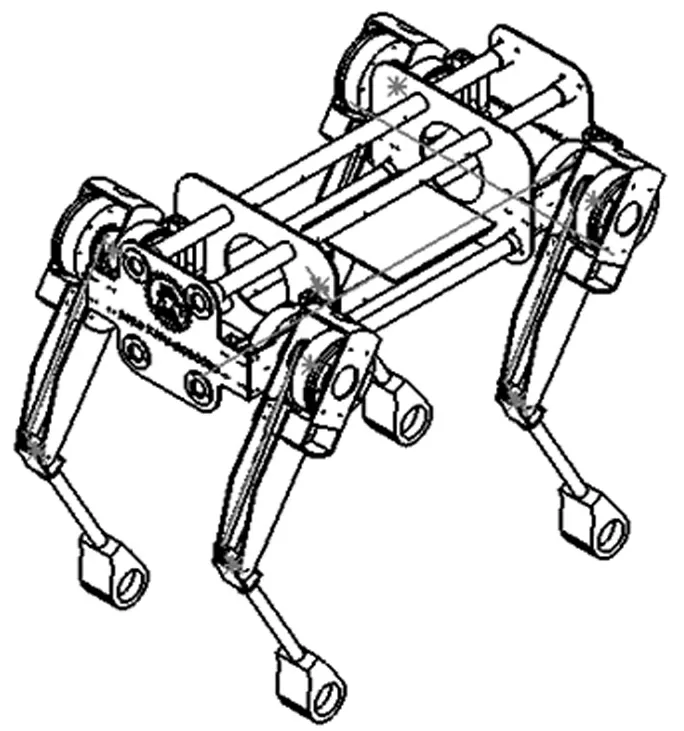
圖1 四足機器人設(shè)計模型

1.1 D-H坐標系建立

如圖2所示，根據(jù)D-H（）法對四足機器人建立坐標系。據(jù)此進行各坐標系的坐標轉(zhuǎn)換，對跳躍過程進行運動學(xué)分析。

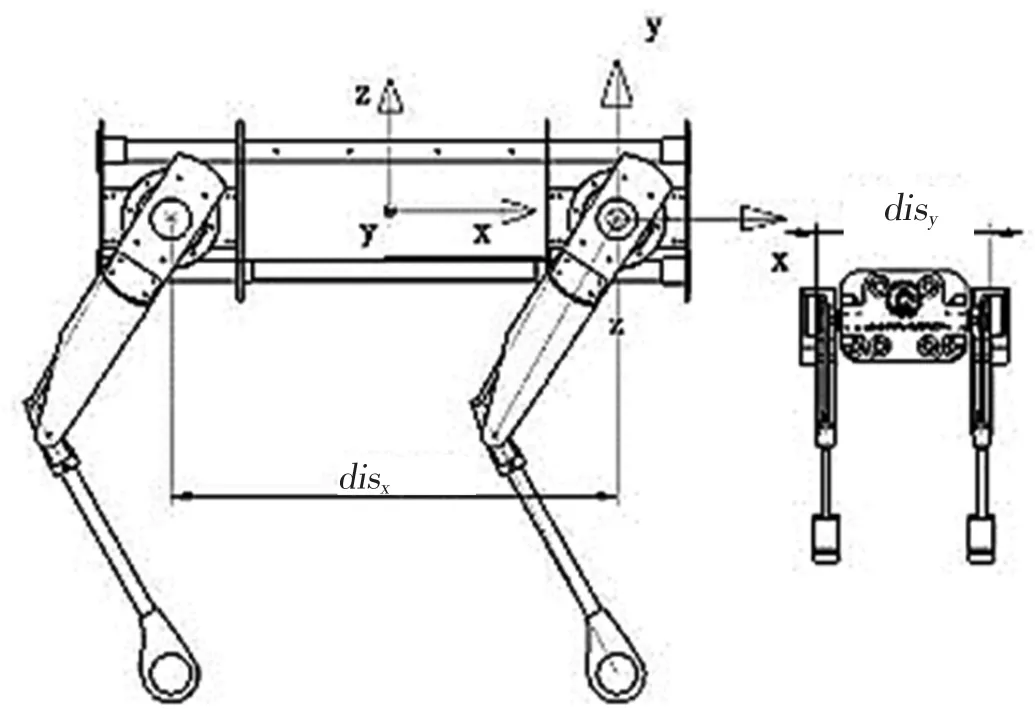
圖2 四足機器人運動學(xué)坐標系坐標圖

在軀體的幾何正中心建立身體坐標系{Ob}，前進方向為x軸的正方向，豎直向上為z軸的正方向。以順時針方向?qū)λ臈l腿分別編號為1，2，3，4。在每條腿的髖關(guān)節(jié)建立坐標系{Oih}（i=1，2，3，4），{Oih}的x軸正向為豎直向下方向，z軸正向為前進方向。同理，對膝關(guān)節(jié)建立坐標系{Oik}，以足端為原點建立坐標系{Oit}。由此可得身體坐標系到髖關(guān)節(jié)坐標系的轉(zhuǎn)換矩陣N如式（1）。以左前腿為例，設(shè)足端運動軌跡在身體坐標系下的函數(shù)為z=f（x，y）。由足端在身體坐標系下的坐標P知足端在髖關(guān)節(jié)坐標系下的坐標P0。由此可以逆解出大小腿電機旋轉(zhuǎn)角度。

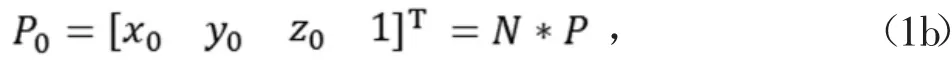
式中，disx為前兩腿髖關(guān)節(jié)間距；disy為同側(cè)兩腿髖關(guān)節(jié)間距。

1.2 跳躍軌跡規(guī)劃

1.2.1 起跳階段軌跡規(guī)劃

起跳階段需保證足端與接觸地面有足夠的摩擦力，即在跳躍過程未發(fā)生相對滑動，同時髖關(guān)節(jié)相對于足底坐標應(yīng)該滿足以下條件：

（1）初始機身高度為y0，水平位移為0m離地前機身高度為y1，水平位移x1；

（2）初速度為0m/s，離地前速度為v1；

（3）初加速度為0m/s2，離地前，豎直加速度為-g，水平加速度為ax1。

在起跳階段，足底在大地坐標系下位置固定，故以足底為參考，規(guī)劃機器人質(zhì)心的運動方程。由于在起跳階段，四腿同時起跳，動作一致，可只考慮單腿的運動。如圖3所示，設(shè)機身質(zhì)心在起跳階段，水平加速度ax（t）=k1t，豎直加速度ay（t）=k2t（k1、k2為常系數(shù)），則水平位移為，豎直位移為

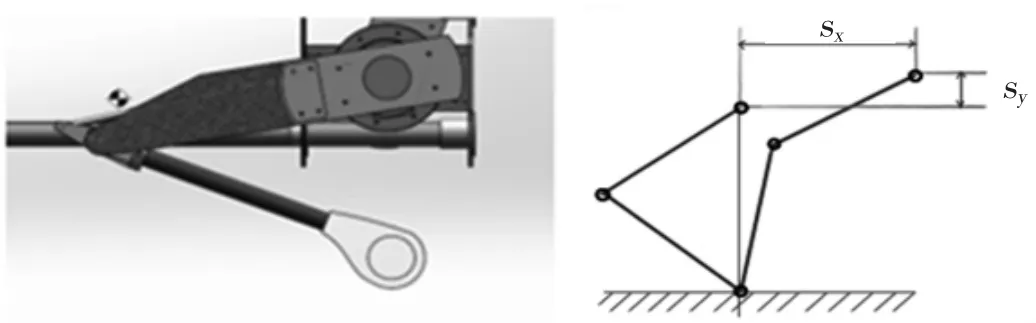
圖3 跳躍階段單腿示意圖

由于髖關(guān)節(jié)的運動軌跡與質(zhì)心同步，設(shè)足端為原點O，髖關(guān)節(jié)的坐標為B（PX，PY），建立如圖4所示坐標系。

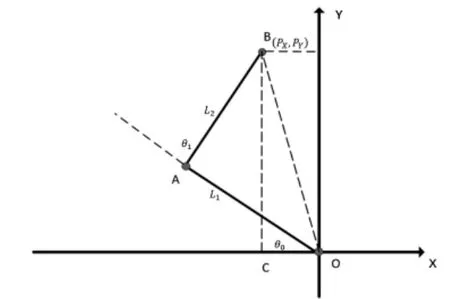
圖4 起跳階段腿部關(guān)節(jié)坐標系

起跳階段D-H參數(shù)見表1。

表1 起跳階段D-H參數(shù)

髖關(guān)節(jié)在基坐標的轉(zhuǎn)換矩陣：

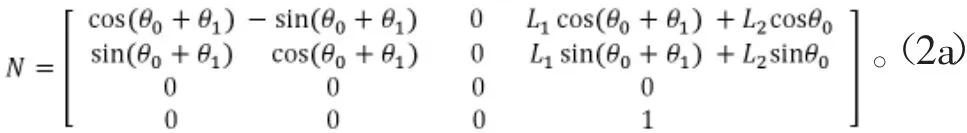
利用幾何解析法對起跳階段做逆運動學(xué)分析，由此得到關(guān)節(jié)轉(zhuǎn)動角度函數(shù)：

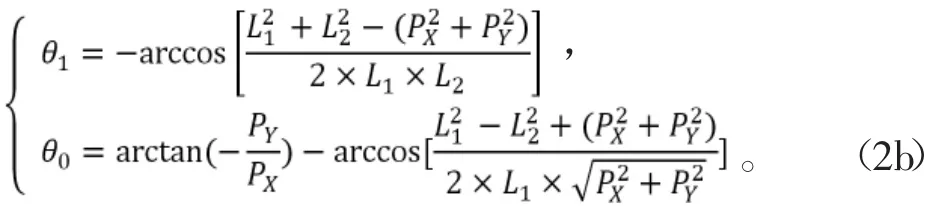
1.2.2 騰空階段軌跡規(guī)劃

足端離地后，機器人處于僅受重力作用的騰空狀態(tài)。在騰空階段機器人機身做類平拋運動，即機身在豎直方向由于以-g為加速度的勻變速運動。同時，在起跳離地時刻與著地時刻，足端與地面接觸且速度均為0。在騰空階段，在跳躍過程中足端有伸縮。

對于質(zhì)心而言，跳躍階段機身質(zhì)心運動軌跡為：

式中，νx1為起跳結(jié)束時刻水平速度；νy1為豎直速度。如圖5，以髖關(guān)節(jié)為原點建立坐標系：

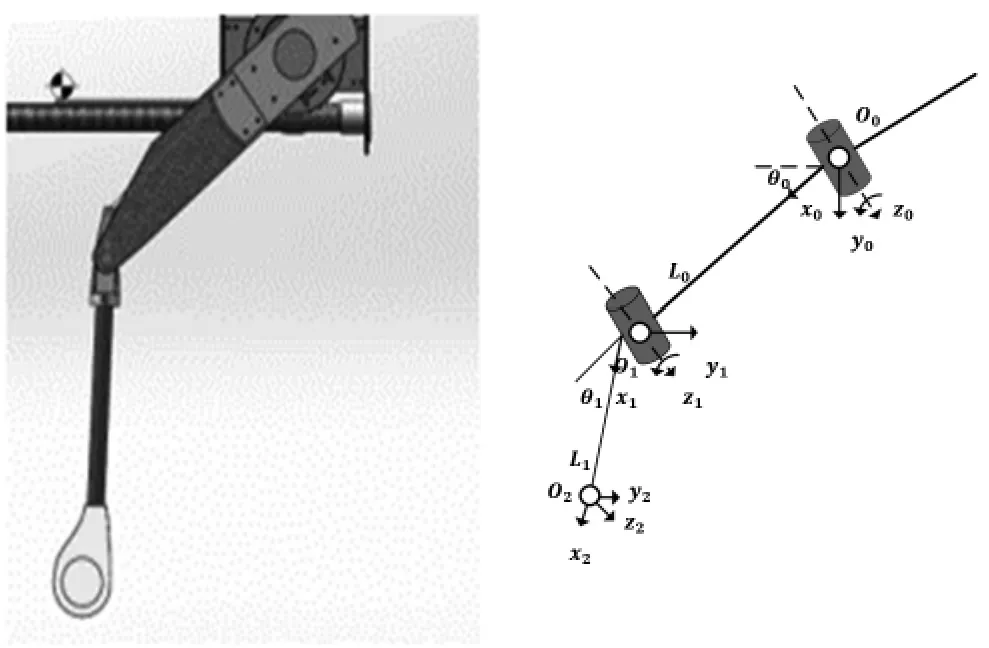
圖5 騰空階段腿部關(guān)節(jié)坐標系

足端在基坐標的轉(zhuǎn)換：

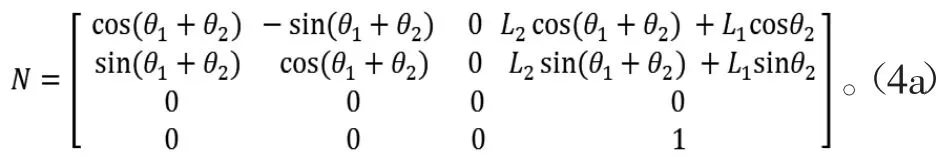
得到跳躍過程中的角度驅(qū)動函數(shù)：

跳躍機器人有一定的越障能力，欲得到跳躍跨越的最大障礙物高度極限H。用sin函數(shù)曲線以及二階多項式擬合足端軌跡，規(guī)劃足端軌跡：

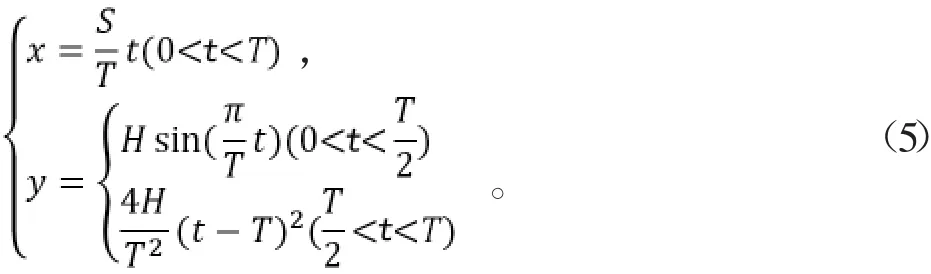
1.2.3 著地階段軌跡規(guī)劃

足端著地后，此時地面有足夠的摩擦力，即無相對滑動。在電機力矩驅(qū)動下產(chǎn)生與機身慣性相反的作用力，使得機器人的速度減小直至為0m/s。著地階段可視為起跳階段的逆過程。同樣，此時足端固定，如圖6，建立坐標系。著地階段質(zhì)心的位移曲線為

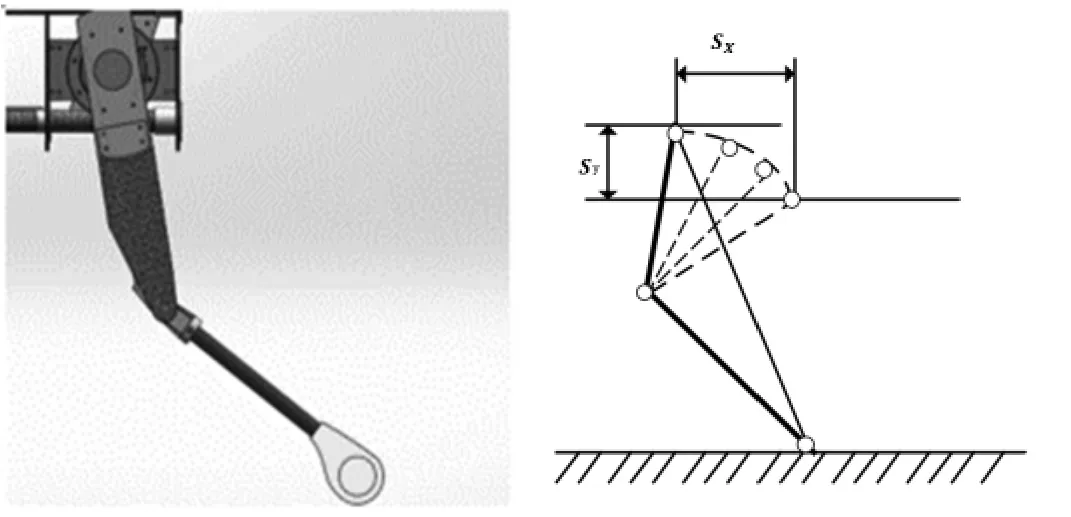
圖6 著地階段腿部關(guān)節(jié)坐標系

2 動力學(xué)建模

四足機器人關(guān)節(jié)數(shù)較多，整個系統(tǒng)有多個輸入輸出，力學(xué)關(guān)系較為復(fù)雜。本文采用Lagrange法以及D'Alembert's原理對其進行動力學(xué)分析，根據(jù)運動規(guī)劃，求解跳躍過程中各關(guān)節(jié)驅(qū)動力矩，進而得到電機的驅(qū)動力函數(shù)。

力矩控制的靈敏度更高，控制方式以及動態(tài)性能更好。如圖7所示，建立跳躍過程中的受力分析圖：

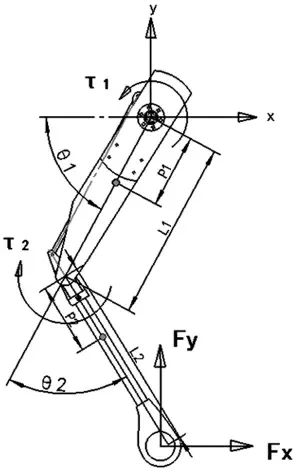
圖7 四足機器人單腿的受力分析

單腿物理參數(shù)見表2。

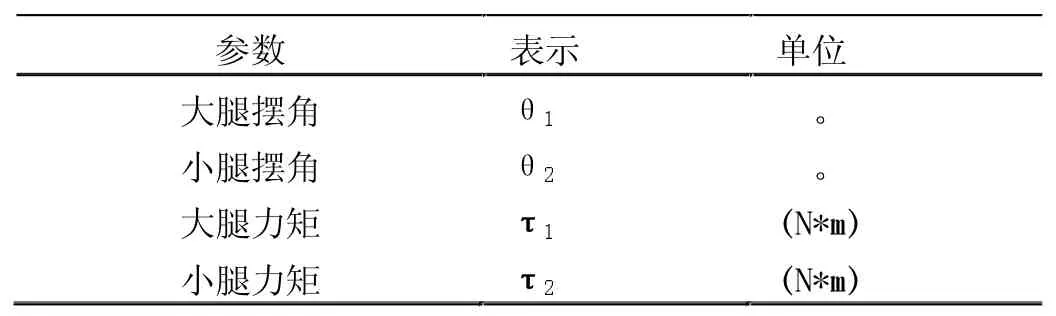
表2 單腿物理參數(shù)

設(shè)定整個機器人的機械結(jié)構(gòu)均為剛性，不發(fā)生柔性變形，同時忽略關(guān)節(jié)間的相對摩擦以及物理樣機裝備過程的誤差。由于起跳階段動力較為簡單，此處僅討論騰空與著地階段的動力學(xué)分析。與運動學(xué)分析類似，建立如圖7坐標系。

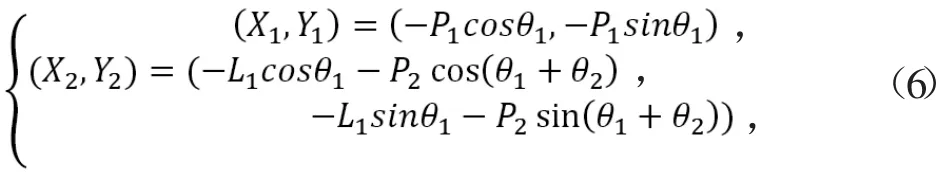
式中，P1為大腿質(zhì)心到髖關(guān)節(jié)距離；P2為小腿質(zhì)心到膝關(guān)節(jié)距離（X1，Y1）為大腿質(zhì)心坐標；（X2，Y2）為小腿質(zhì)心坐標。此時動能Ek，勢能Ep為：

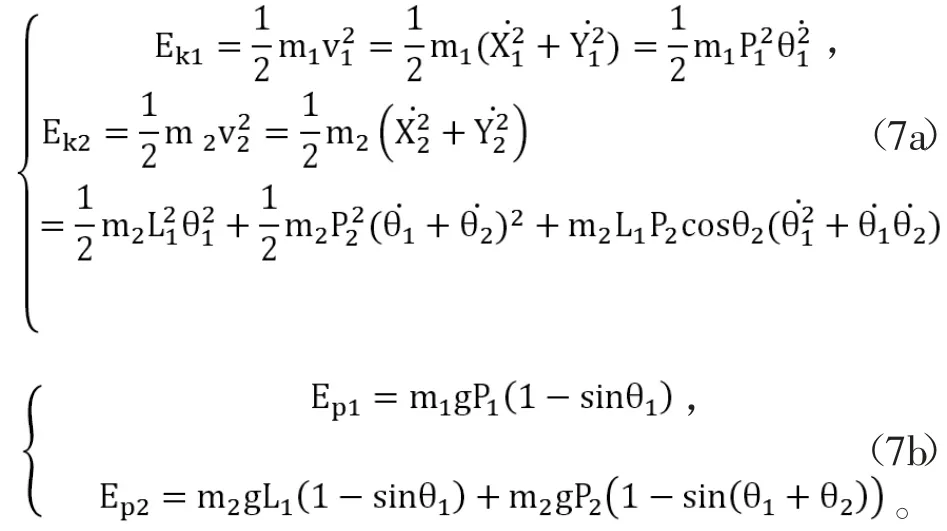
得到Lagrange函數(shù)：

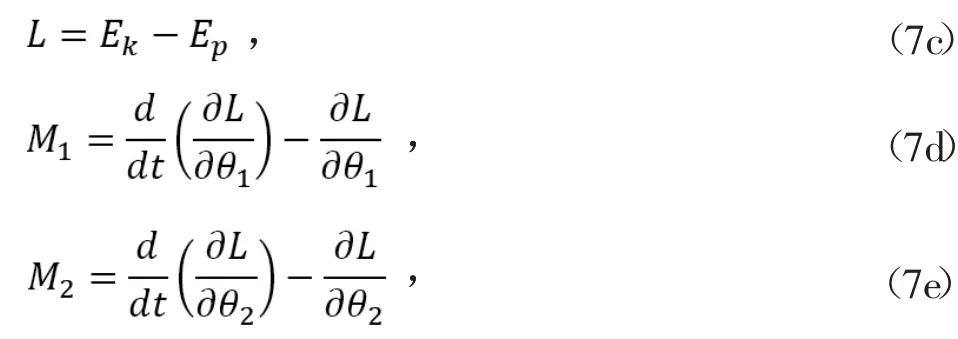
式中，M1為髖關(guān)節(jié)驅(qū)動力矩；M2為肘關(guān)節(jié)驅(qū)動力矩。

著地后，由于機身具有慣性，此時需要反方向的作用力，設(shè)此時足端與地面無相對滑動，地面給機器人的靜摩擦力。根據(jù)D'Alembert's原理，對單腿力矩平衡分析得到：

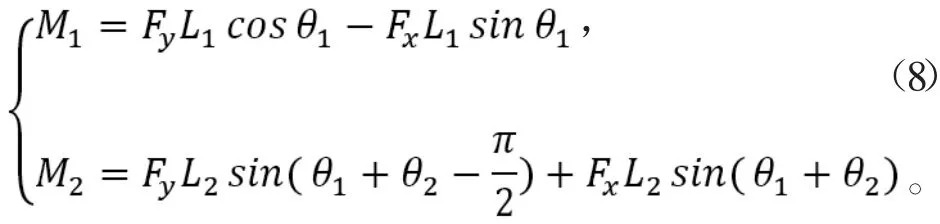
如圖8，對整體進行受力分析，由于跳躍過程中軀干是平動，質(zhì)心處力矩為0，根據(jù)受力平衡與力矩平衡，得到式（9）的力學(xué)方程。

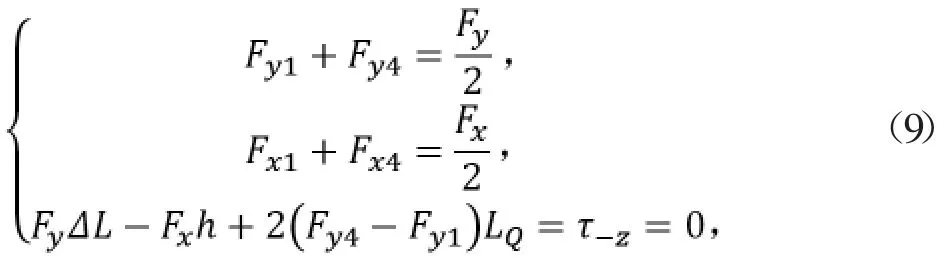
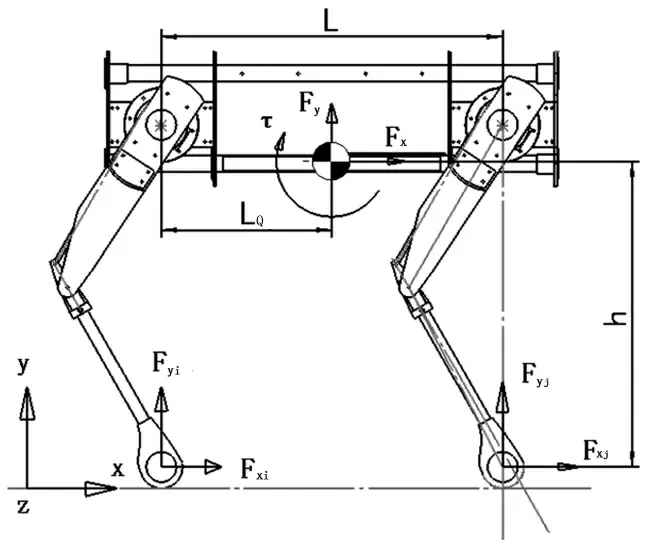
圖8 四足機器人整體的受力分析

式中，F(xiàn)xi、Fyi為第i條腿足端的水平與豎直方向的力，F(xiàn)x Fy為質(zhì)心受到的水平與豎直方向的力，LQ為質(zhì)心到髖關(guān)節(jié)的水平距離。

根據(jù)軌跡規(guī)劃可知大腿、小腿角加速度在開始準備跳躍的一瞬間發(fā)生突變，同時在離地和著地的瞬間有微小突變，由此引發(fā)力矩的突變。

在力矩控制中，可對這兩次的突變進行一個平滑的曲線過渡，可有效減小四足機器人運動過程中受到的沖擊力。

Fx1作為可變參數(shù)，結(jié)合前面驅(qū)動力矩公式得到相應(yīng)驅(qū)動函數(shù)，利用MATLAB求解出如圖9髖、膝關(guān)節(jié)力矩變化。由力矩圖觀察可得Fx1取時，即取Fx1=Fx4分析得到的力矩為最優(yōu)解。

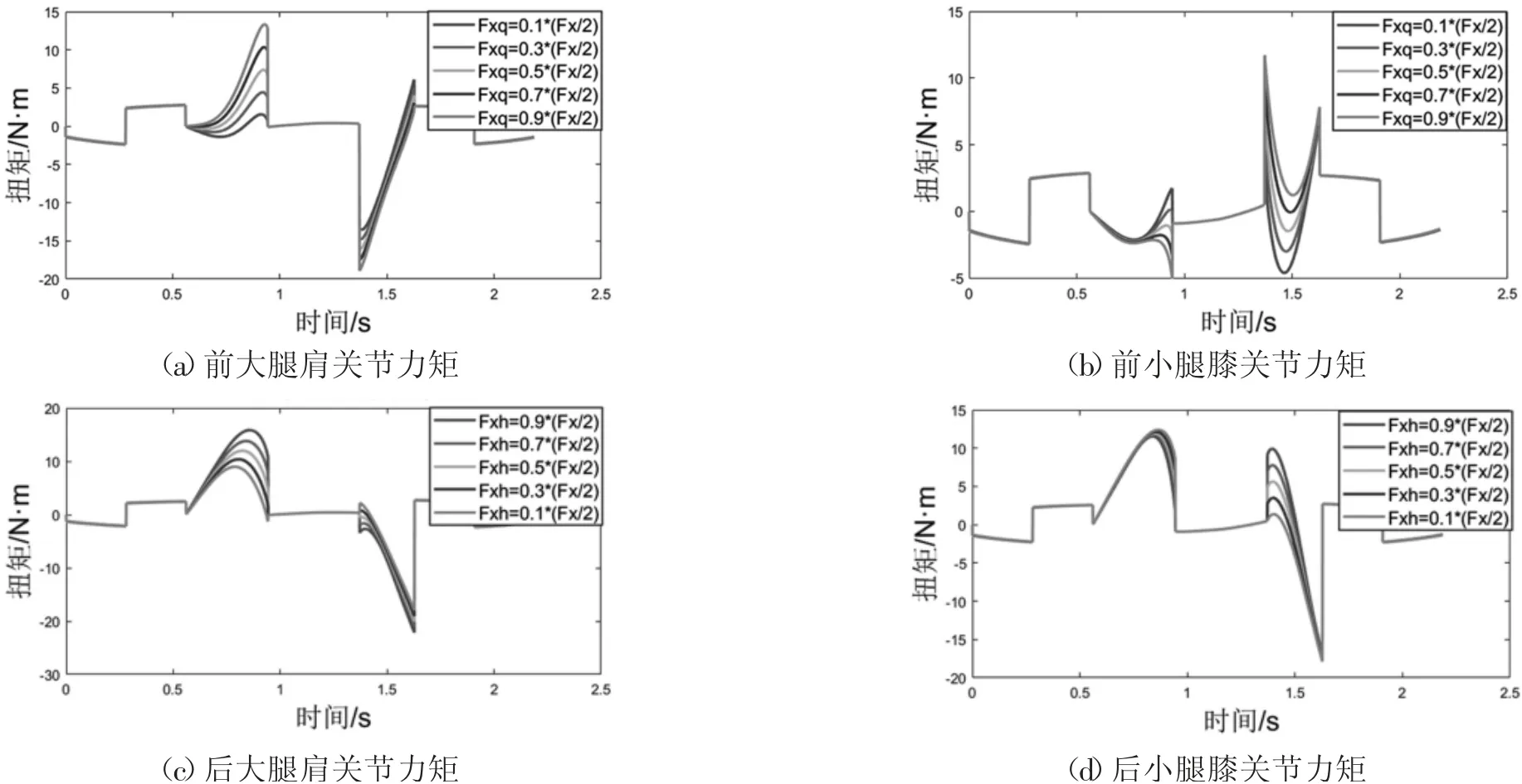
圖9 髖、膝關(guān)節(jié)力矩變化曲線圖

3 仿真研究

利用SolidWorks建立機器人得機械模型，并基于MATLAB中的Simulink模塊搭建四足機器人系統(tǒng)，聯(lián)合ADAMS進行模擬實際跳躍過程。

3.1 物理樣機跳躍軌跡規(guī)劃

根據(jù)上述的軌跡規(guī)劃，對物理樣機探究其跳躍階段的最大限度。根據(jù)樣機參數(shù)（如表3所示），跳躍時取每條腿的輸出扭矩為T=18N·m，則跳躍時對地面的作用力為

表3 物理樣機參數(shù)

設(shè)初始時，小腿與地面夾角為φ，大小腿夾角（外角）為ω，則根據(jù)規(guī)劃的軌跡，加速度a在起跳過程中與時間t成線性關(guān)系，則有k1=

為了使同一腿上兩個電機在起跳過程中都能以最優(yōu)效率輸出，應(yīng)使髖關(guān)節(jié)即身體質(zhì)心的運動軌跡和足端接觸點與髖關(guān)節(jié)中心的角度α盡量小，故需要對起跳的姿態(tài)進行調(diào)整，而起跳的姿態(tài)主要由小腿與地面夾角φ以及大小腿夾角ω決定，通過MATLAB對φ∈（40°，70°），ω∈（130°，160°）進行迭代分析。得到：φ越大，α越小，在ω=158°時α有最小值。考慮機械結(jié)構(gòu)的限制，取ω=148°。

由于φ與起跳階段加速度及時間都有關(guān)，進而影響到跳躍的高度以及距離，為求得最優(yōu)的高度與距離，通過非線性規(guī)劃來得到φ的值。建立非線性規(guī)劃問題：

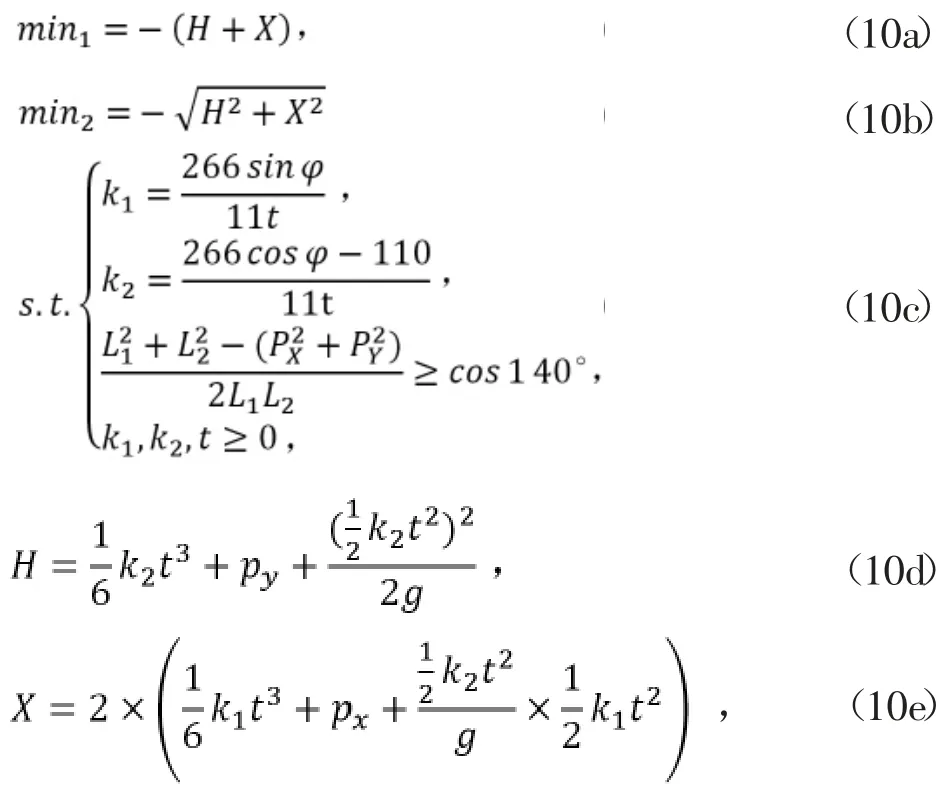
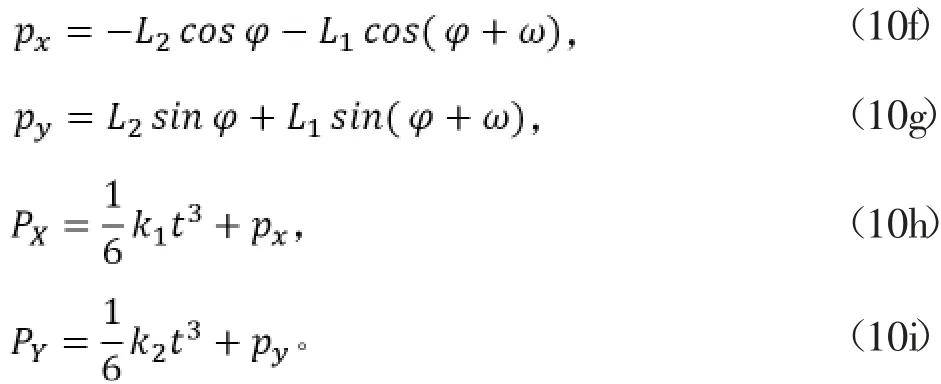
式中，（px，py）為開始起跳時髖關(guān)節(jié)較足端與地面接觸點的相對位置；(PX，PY)為起跳階段結(jié)束時髖關(guān)節(jié)相對于足端接觸點的位置；H、X分別為跳躍的高度和距離。

利用MATLAB得到目標函數(shù)最優(yōu)時，此時a=25.7°，t=0.384s。得到機身質(zhì)心軌跡隨時間變化的函數(shù)：

根據(jù)得到的質(zhì)心與足端的運動軌跡函數(shù)，得到如圖10的一個跳躍周期膝、髖關(guān)節(jié)角度變化曲線。

由圖10可以分析得到，在起跳階段，機體的前伸主要靠膝關(guān)節(jié)擺動，因此膝關(guān)節(jié)角度以較大幅度增加，而髖關(guān)節(jié)角度逐漸減小；在騰空期前期，膝關(guān)節(jié)的擺動對機體的豎直運動起主要作用；在跨越期間，髖關(guān)節(jié)角度變化較快，膝關(guān)節(jié)先收縮再伸展；著地后，恢復(fù)初始角度。

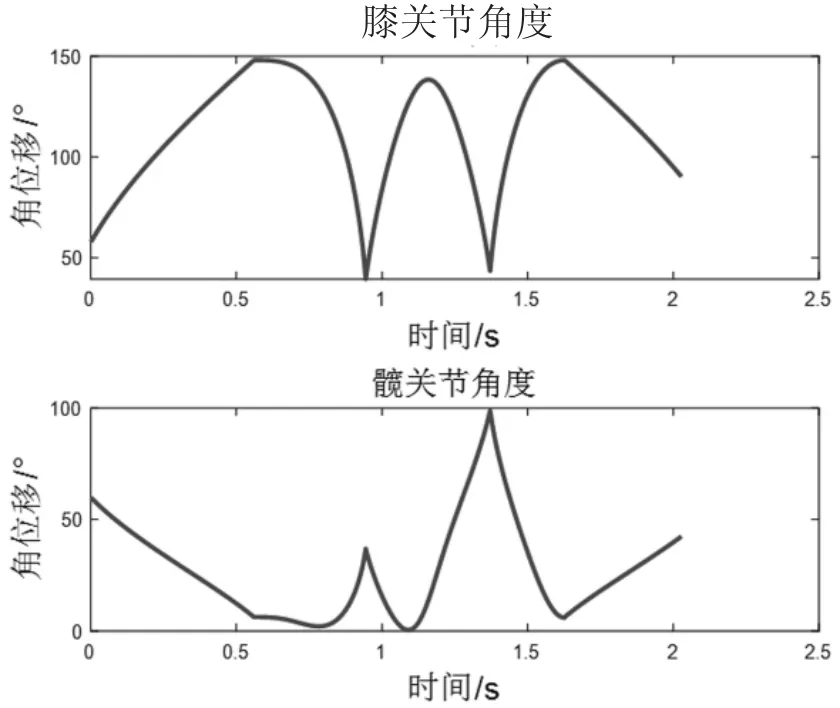
圖10 膝、髖關(guān)節(jié)角位移變化曲線圖

3.2 運動學(xué)仿真

通過前文規(guī)劃的四足機器人在跳躍過程中的機身質(zhì)心運動軌跡以及足端運動軌跡，通過正逆運動學(xué)分析，得到每條腿關(guān)節(jié)轉(zhuǎn)角方程，仿真過程如圖11所示。

圖11 關(guān)節(jié)轉(zhuǎn)角函數(shù)的運動分解圖

為驗證規(guī)劃曲線的合理性與魯棒性，借助ADAMS得到機身質(zhì)心在水平與豎直方向位移與速度的變化圖，如圖12所示。

在整個跳躍周期內(nèi)，通過圖12可以看出整個機身在水平方向的跳躍軌跡與之前規(guī)劃的運動軌跡基本一致，在某些節(jié)點處，如起跳著時的速度變化有較大起伏，最大偏差約為0.5m/s，但由于偏差時間較小，對整體運動軌跡影響較小。

圖12 中質(zhì)心水平方向偏移表明整個跳躍過程中機身較為穩(wěn)定，但在著地的瞬間豎直方向質(zhì)心會有0.005m的偏差，主要原因是在騰空階段對身體角度的調(diào)整不夠，使得下落時后腳先著地從而引起較小的偏差，可以通過加大騰空階段的下落過程中小腿擺動角加速度，使身體下落時質(zhì)心運動角度向下，機身更加平穩(wěn)著地。

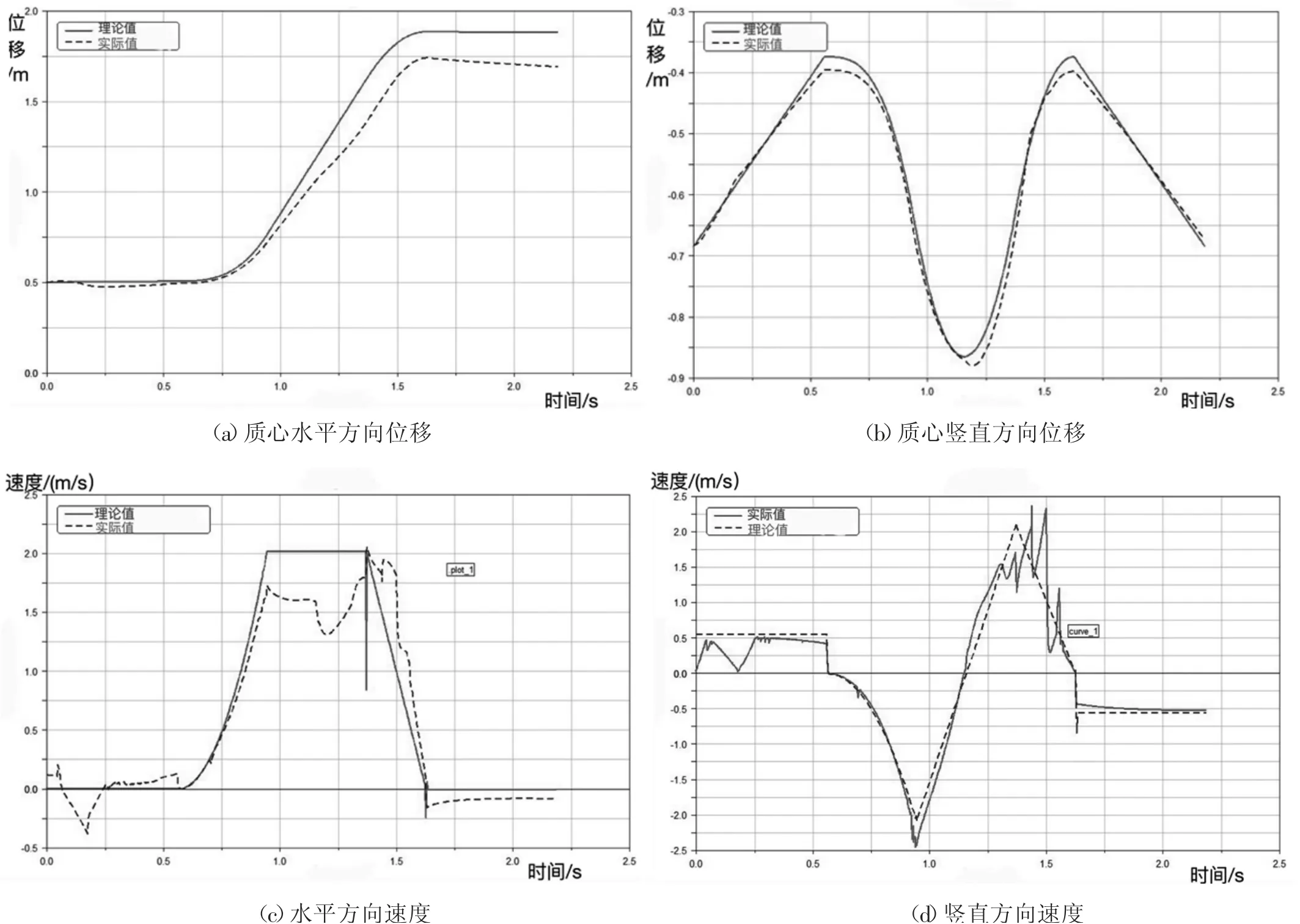
圖12 跳躍過程各參數(shù)變化圖

3.3 動力學(xué)仿真

整個機器人為鋼體結(jié)構(gòu)，與地面接觸碰撞過程較為復(fù)雜，同時為驗證規(guī)劃的運動軌跡的正確性與合理性，故將前文得到的力矩驅(qū)動函數(shù)施加在ADAMS中對機器人模型的各腿的髖關(guān)節(jié)與肘關(guān)節(jié)，進行動力學(xué)仿真。跳躍過程，四足機器人的運動分解姿態(tài)如圖13。從圖13中可以看出，機身質(zhì)心與足端的運動軌跡與規(guī)劃的曲線基本一致。起跳階段，獲得向上以及向前的驅(qū)動力矩，肘關(guān)節(jié)變化較大，在起跳過程中起主要作用。騰空階段，腿部有收縮，同時機身做類平拋運動。在著地階段，機身減速，重心降低。

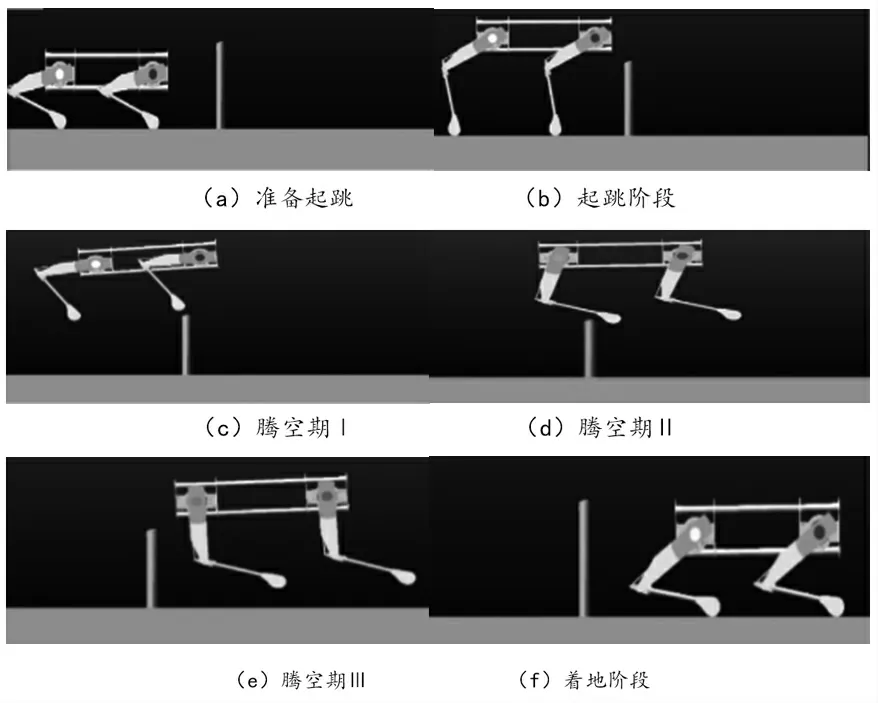
圖13 關(guān)節(jié)力矩函數(shù)的運動分解圖

水平與豎直方向的位移與速度的變化趨勢如圖14所示。在離地和著地的瞬間大小腿角加速度有微小突變，由此引發(fā)力矩的突變。可對這兩次的突變進行一個平滑的曲線過渡，減小四足機器人運動過程中受到的沖擊力。仿真結(jié)果與理論值基本一致，驗證了前文規(guī)劃曲線以及力矩驅(qū)動函數(shù)的正確性。

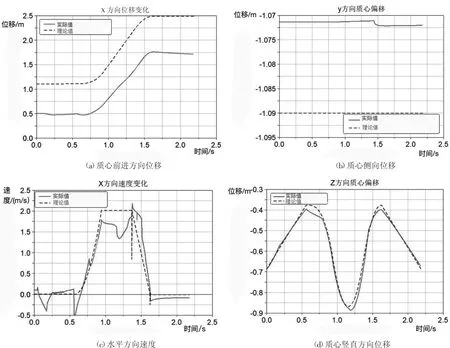
圖14 跨高欄全過程控制效果圖

4 結(jié)束語

根據(jù)四足動物跳躍運動特性，本文將跳躍過程分為起跳、騰空和著地三個階段分別進行運動曲線的規(guī)劃。通過正逆運動學(xué)分析得到了關(guān)節(jié)轉(zhuǎn)角控制函數(shù)，并基于Lagrange法以及D'Alembert's原理進行動力學(xué)分析推導(dǎo)出力矩驅(qū)動控制函數(shù)。利用SolidWorks建立物理樣機模型，利用ADAMS聯(lián)合MATLAB搭建仿真平臺。進行了物理樣機的運動學(xué)、動力學(xué)仿真，將仿真結(jié)果與理論值進行比較，從而驗證了跳躍運動規(guī)劃曲線的可行性與正確性，以及角度控制、力矩控制的準確性與魯棒性，為后續(xù)四足機器人或其他跳躍型機器人控制規(guī)劃以及仿真實驗的研究提供了基礎(chǔ)。