高速列車車體隨機振動仿真預測與試驗驗證
林松,孫明道,朱建華
(中車青島四方機車車輛股份有限公司技術中心,山東 青島 266111)
隨著高速列車速度的不斷提升,振動噪聲問題日益嚴峻。列車不僅需要具備足夠的靜剛度來維持承載能力,還更應具有合理的動態特性以抑制車體的振動噪聲。由于列車運行過程中車體結構所受激勵具有明顯的隨機性,產生的振動噪聲也具有明顯的隨機性。因此,研究高速列車車體的隨機振動響應特性,對于控制列車振動噪聲具有重要的意義。
在結構隨機振動噪聲問題的研究中,劉寶山等基于有限元法、邊界元法和虛擬激勵法,研究了結構隨機振動聲輻射靈敏度及優化設計問題,該方法計算精度與傳統方法等價,且計算效率高;Zhao等在虛擬激勵法基礎上采用新的算法計算了結構隨機激勵下的振動問題,其在計算效率上與虛擬激勵法相比具有絕對的優勢;Mehran等利用ABAQUS軟件對軌道車輛車廂進行了隨機振動仿真分析。
綜上,目前已對列車在確定激勵下的振動和噪聲問題開展了一系列的研究,但多數局限于有限元仿真研究,對實車隨機振動的試驗驗證研究較少。本文以實車結構為研究對象,通過模型簡化和車體網格細化分析,建立有限元模型與實際試驗結果不斷修正對比,形成了適合高速列車實際應用的有效模型和研究方法。
1 車體有限元建模及試驗驗證
1.1 車體有限元建模
模型簡化。選取高速列車端部實車結構為研究對象,試驗車體長度為7m,車體兩端均帶外端,車體重量約為3.2噸,所用材料為鋁合金,材料參數如表1所示。

表1 試驗車體材料參數
對軌道車輛而言,車體結構整體以薄板結構為主。考慮到車體結構的復雜性及車體型材特點,在盡量保持結構不變的條件下,為提高有限元建模效率和縮短仿真計算時間,將車體簡化為殼單元進行建模,同時刪除過渡圓角等對結構性能影響較小的工藝結構,其中,車體蒙皮取外表面,筋板取中性面,簡化前后的三維幾何模型如圖1所示。
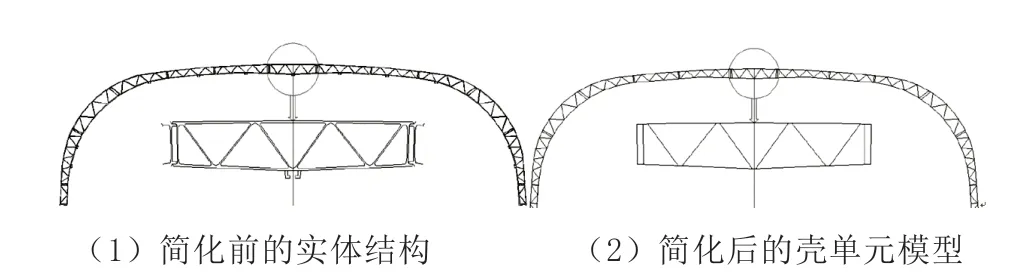
圖1 車頂及側墻結構簡化
1.2 車體網格細化分析
車體幾何尺寸和材料參數見表2。

表2 幾何尺寸和材料參數
當計算頻率為500Hz,板厚度為1.8~12mm時,根據表2各參數,可得單元邊長的大致范圍為Δ≤0.0472~0.1218m,即47.2~121.8mm之間。整體選取幾組不同網格單元長度分別計算,即選取不同的單元尺寸對車體進行全局網格劃分,然后計算車體隨機響應,并得到振動加速度響應的均方根值,如表3所示。
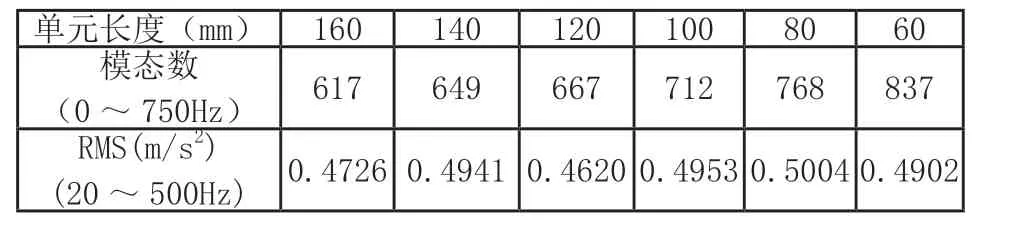
表3 振動加速度響應與有限元網格劃分細化程度對比關系
從表3可以看出,網格越密,加速度響應數值越趨于穩定。由于車體結構較為復雜,模態較為密集,不易找到模態突變數。當網格單元長度為60mm時,模態數和加速度均方根值均趨于穩定,因此,在后續進行隨機振動響應分析時,采用全局網格單元長度為60mm車體有限元模型。如圖2所示。

圖2 試驗車體有限元模型
1.3 車體計算模態及試驗模態分析
由于仿真計算建模過程中進行了若干簡化,需通過模態試驗校驗仿真模型的準確性。模態試驗中,試驗車體采用彈性支撐,測試在近似自由狀態下的模態參數;然后,通過電磁激振器產生激勵信號,并由動態數據采集系統采集信號;最后,進行車體模態分析。試驗車體模態測試測點布置如圖3所示。計算結果與試驗結果對比見表4。

圖3 試驗車體彈性支撐
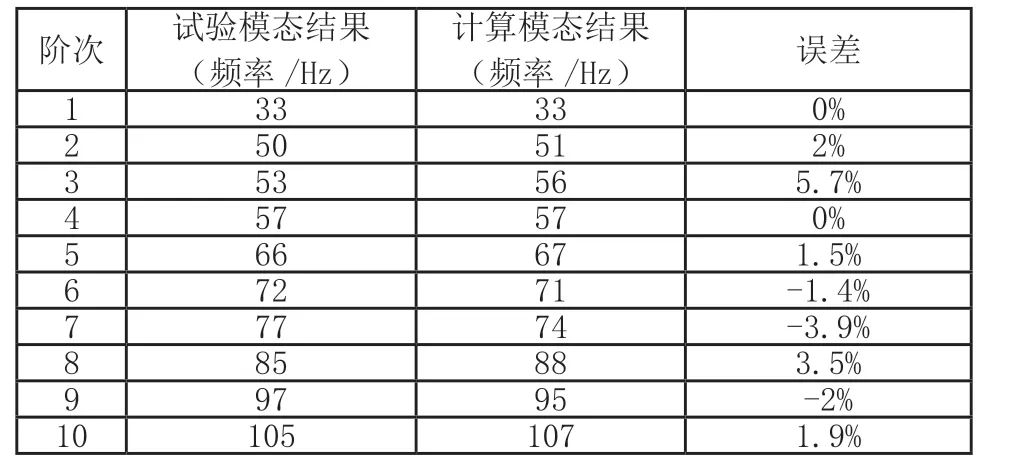
表4 計算結果與試驗結果對比
從表4中可以看出,模態的計算結果與試驗結果最大誤差為5.7%,振型基本一致,仿真計算的準確度較高,可替代實車結構用于隨機振動分析。
2 車體隨機振動預測與分析
為保證車體隨機振動噪聲預測模型能夠較為準確地替代實車結構,采用東菱ES-10-240電動振動臺采集車體隨機振動和噪聲信號,進行振動和噪聲試驗。在進行隨機振動試驗前,先進行關心頻段內的預試驗,了解系統的振動特性。根據車體振動試驗的激勵位置,在仿真模型的轉向架位置施加隨機基礎激勵(頻率范圍20~200Hz,步長1Hz),隨機振動控制曲線均在3dB控制容差限以內。仿真結果與試驗結果對比見圖4。
如圖4,仿真結果與試驗結果主要峰值頻率基本一致,但在幅值以及次要峰值頻率上存在一定的區別,與試驗測試誤差、仿真模型簡化以及模態阻尼參數的設置等存在較大的關系。
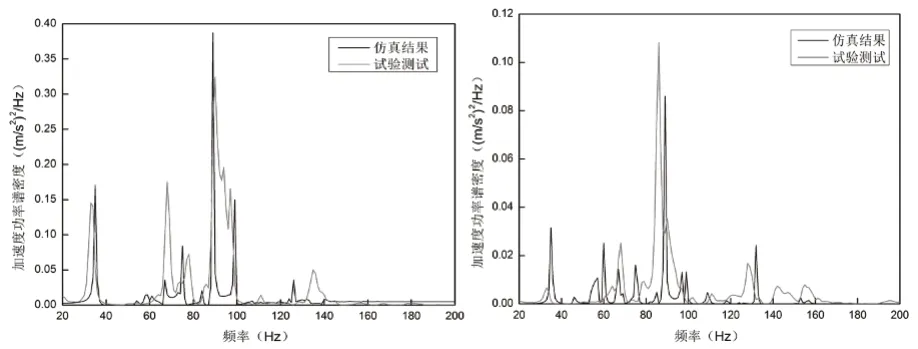
圖4 仿真結果與試驗結果對比-加速度功率譜密度曲線
3 結語
(1)通過模態試驗和仿真對比,表明試驗車體有限元模型具有較高的精度;(2)對試驗車體進行隨機振動預測與試驗分析,可知車體振動能量主要集中在60~110Hz的頻率范圍內,合理控制該頻段內的振動能量,在一定程度上能起到減振降噪的目的;(3)選取點的振動加速度功率譜密度幅值仿真結果與試驗結果主峰值頻率基本一致,但在幅值以及次要峰值頻率上存在一定的區別,主要與試驗測試誤差、仿真模型簡化以及模態阻尼參數的設置等有關;(4)對車體隨機振動噪聲問題的研究,能夠在設計早期對車輛的振動噪聲特性進行評估,減少減振降噪對策滯后的問題。

