某高架立體倉庫抗風柱設計探討

彭 磊

(中國海誠工程科技股份有限公司，上海 200031)

隨著土地資源的日益緊張和人工成本攀升，物流自動化技術越來越廣泛的應用于各個工業領域。物流自動化技術大規模應用催生了大量立體倉庫的配套建設。而考慮土建成本的因素決定了立體倉庫的結構形式還是門式剛架。但是相比于常見的低矮輕型門式剛架，立體倉庫的剛架結構高寬比大得多，一些在低矮門式剛架結構中不需要特別考慮的問題因此需要引起設計人員的注意。本文以某高架立體倉庫結構設計為例，探討和比較了高架立體倉庫的山墻面抗風柱設計的三種方案，分別從經濟性和結構設計難易程度方面做了比較，探討結論可以為類似的工程借鑒參考。

1 工程概況

某造紙企業存放成品的高架立體倉庫，檐口高30 m，長寬為73 m×49 m。內部設置局部單層鋼平臺。整體結構形式采用單跨49 m剛架，內部單層鋼平臺與剛架整體連接在一起。

工程所處自然條件，基本風壓0.40 kN/m2，基本雪壓0.4 kN/m2。對于此類鋼結構，地震作用對整個結構基本都不起控制作用，往往地震作用的設計內力遠小于風荷載造成的設計內力，故本文不做抗震設計內容的討論。

結構整體模型如圖1所示。由于山墻面斜梁最高處達到31 m，對應處的抗風柱高度也達到了30 m，如何保證該抗風柱設計兼顧經濟性和結構合理性，為此需要特別考慮。本文提出了三個方案應用于此類高大抗風柱的設計，以下詳細探討。

2 高大抗風柱設計方案探討

2.1 方案一

方案一采用通高抗風柱，抗風柱與屋面斜梁鉸接連接，鉸接節點可以釋放豎向位移，方案一結構簡圖見圖2。根據《門式剛架輕型房屋鋼結構技術規范》(后文簡稱“門規”)，可以設置隅撐減小抗風柱平面外彎扭穩定的計算長度，平面外彎扭穩定對抗風柱要求不高。但是，此類高大抗風柱上承受的墻檁和外墻荷載都較大，軸壓造成的彎曲穩定性隨著抗風柱的高度增加，要求會越來越大。如果考慮利用墻檁提供平面外側向支撐，需要墻檁承受一定的軸壓力。然而當前鋼結構設計標準沒有提供多根立柱在有多道支撐時的支撐力的計算方法。因此，只能被動的采用抗風柱全長作為平面內和平面外計算長度，抗風柱的截面必須做到足夠大才能滿足穩定性要求。

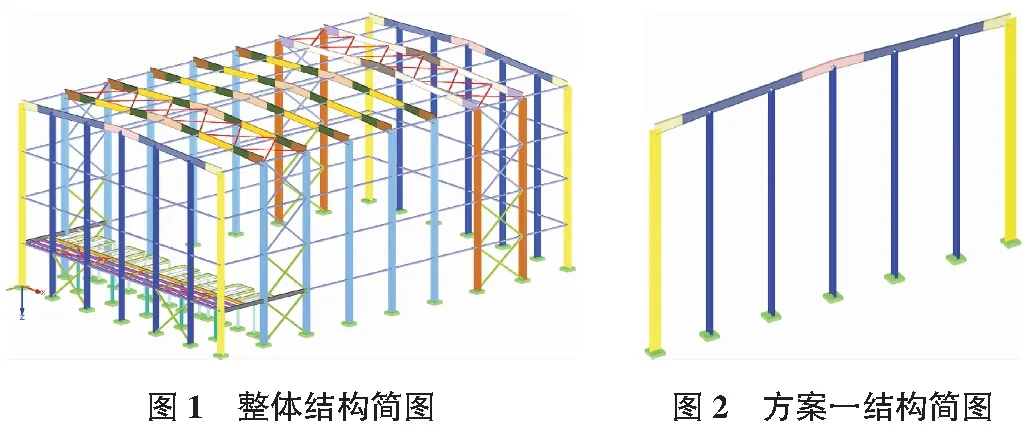
值得注意的是，剛架在抗風柱頂為抗風柱提供了平面外穩定支撐，剛架柱的計算長度應該考慮類似于搖擺柱的影響，也需要乘以類似于“門規”A.0.6條的放大系數η。但由于抗風柱沒有承受斜梁的豎向力，剛架柱的計算長度并不能套用“門規”中帶有搖擺柱的計算長度修正系數，況且“門規”也不允許單跨剛架設置如此多搖擺柱。因此建議采用有限元整體屈曲分析的方法求解剛架柱的計算平面內計算長度，方法可以參考下文方案二。

本方案的優點是力學概念清晰，受力合理。因為低矮的門式剛架抗風柱設計通常采用，所以結構做法和構造措施成熟。

本方案的缺點是抗風柱的截面較大，經濟性不好。

例如，本項目中抗風柱最長取31 m，間距8.5 m，抗風柱柱腳剛接，抗風柱按照圍護構件設計，當采用方案一，設置側向隅撐，且考慮隅撐對抗風柱的受壓翼緣側向約束，考慮到抗風柱與上部斜梁連接，采用H型截面。此時平面外長細比和平面外穩定承載力起控制作用，采用H型截面500(高)×800(寬)×16(腹板)×30(翼緣)，截面重量為415.5 kg/m，平面外長細比為144，穩定應力比0.93。

2.2 方案二

方案二考慮為抗風柱設置水平柱間系桿，將抗風柱側面與剛架柱聯系起來以減小抗風柱的平面外計算長度，見圖3。抗風柱與屋面斜梁還是采用鉸接連接，且鉸接節點可以釋放豎向位移，抗風柱柱腳剛接。但是如此一來，邊榀剛架柱為抗風柱的穩定提供支撐，剛架柱的計算長度就不能按照“門規”的方式計算。因此需要確定邊榀剛架柱平面內計算長度。同時也需要考慮在這種情況下，抗風柱的平面外計算長度是多少。這兩點沒有現成的公式可以依據，如果求理論解又對設計人員的基本理論要求非常高，因此只能采用有限元整體穩定分析的方法來求解邊榀剛架柱的平面內計算長度和抗風柱的平面外計算長度。

有限元整體穩定分析的理論方法為采用分步加載的方式，直到等式[K][δ]=[F]的左邊小于右邊，也就是外力大于結構整體剛度和位移的乘積，此時結構失穩。即求得結構的整體臨界承載力Pcr。

根據歐拉承載力公式，可由Pcr求得構件的計算長度。

采用有限元軟件完成屈曲分析后，求解某根構件的計算長度時，先找該構件發生失穩的最低模態，必須是該構件自身失穩，而不是由于其他構件失穩帶動的變形。由該模態的荷載系數乘以該構件的軸力值，即求得該構件的Pcr。

本方案的優點是采用簡單的方式就可以控制抗風柱的平面外計算長度，抗風柱不限制剛架的側向位移，抗風柱與剛架的斜梁的節點構造同方案一比較常見，不需要特別考慮。

本方案的缺點是力學概念較為復雜，需要采用有限元整體屈曲分析的方法確定剛架柱的平面內計算長度和抗風柱的平面外計算長度。設計人員對于有限元整體屈曲分析方法的把握和結構屈曲模態的分辨是設計中的難點。需要設計人員具有一定的經驗。

例如本項目通過有限元方法來確定剛架柱的計算長度系數。在本項目所討論的抗風柱結構中，荷載組合(1.3恒載+1.5活載)是造成柱子軸壓力最大的工況。因此取該組合進行整體結構的屈曲分析。在分析中，第一階屈曲模態顯示了抗風柱與剛架一起發生了整體屈曲，如圖4所示。因為抗風柱的穩定幾乎完全依賴剛架，故抗風柱的平面外屈曲和剛架的平面內穩定是一起發生的。因此根據第一階屈曲模態的荷載系數求解剛架柱的平面內穩定計算長度和抗風柱的平面外穩定計算長度。

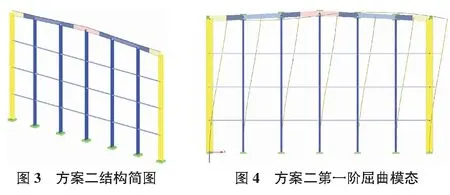
剛架柱軸力最大的截面是在底部一段，根據該段的軸力乘以荷載系數，可以求得剛架柱的平面內計算長度為54.952 m。抗風柱的平面外計算長度為7.59 m。

作為對比，當不考慮剛架為抗風柱提供穩定支撐時，使用PKPM軟件的門鋼模塊，根據“門規”的附錄A計算得剛架柱的平面內計算長度為44.23 m。由此可見當剛架為多根抗風柱提供穩定支撐時，剛架的計算長度比“門規”給的計算長度增大較多，對此需要設計人員引起足夠的重視。

抗風柱彎曲平面內計算長度也可以通過有限元整體屈曲分析的結果來判斷。找到抗風發生平面內屈曲的模態，如圖5所示。

同理，根據抗風柱軸力最大的底部段的軸力乘以該模態的荷載系數，可以求得平面內計算長度為13.59 m，主要是由于柱腳剛接導致的抗風柱平面內計算長度減小。

根據抗風柱平面計算長度7.59 m，平面內計算長度13.59 m驗算抗風柱，采用H型截面800(高)×420(寬)×20(腹板)×24(翼緣)，截面重量為265.7 kg/m，平面外長細比為82.6，穩定應力比0.93。

2.3 方案三

方案三考慮為抗風柱設置多層柱間支撐，抗風柱與邊榀剛架柱形成完整的抗側力體系，如圖6所示。在該種結構體系下，邊榀剛架的設計與抗風柱的設計都可以回歸設計人員較為熟悉的方法。剛架平面外計算長度取縱向支撐的節點間距，平面內的計算長度取與抗風柱之間設置的柱間支撐的節點間距。抗風柱的平面外計算長度取支撐的節點間距，平面內的計算長度可以保守的取全高。不需要再進行結構的整體屈曲分析。

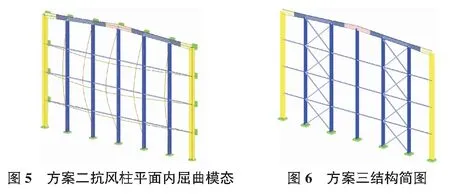
本方案的優點是力學概念清晰，受力合理。容易為設計人員所理解。

本方案的缺點是，抗風柱和柱間支撐組成的體系承受了邊榀框架的風荷載，因此抗風柱和剛架斜梁的節點承受較大的水平力，需要設計時特別考慮，并詳細設計抗風柱與斜梁的連接節點。相比方案二，還需要設計山墻面的柱間支撐。

本方案中，抗風柱彎曲平面外計算長度為支撐的間距，這里取7.5 m，彎曲平面內計算長度取31 m。

經計算，本方案中，抗風柱采用H型截面同方案二，800(高)×420(寬)×20(腹板)×24(翼緣)，截面重量為265.7 kg/m，平面外長細比為82.6，穩定應力比0.92。

2.4 結論分析

以上對高大抗風柱結構的三種方案進行了詳細的分析，論述了各個方案的設計要點和結構設計的難易程度，可以得出如下結論：

方案一，概念清晰，設計較為簡單，抗風柱比較粗壯，需要按照整體屈曲分析確定平面內計算長度。

方案二，設計概念復雜，抗風柱材料較節省，需要按照整體屈曲分析確定剛架和抗風柱的計算長度。

方案三，概念清晰，設計簡單，抗風柱材料較為節省。

因此方案三是此類高大抗風柱設計的最優方案，但如前所述，需要對抗風柱與斜梁的連接節點特別注意，該節點承受了較大的水平力。

還需要注意的是，屋面水平支撐要從第二跨開始設置，第二榀剛架與邊榀剛架采用剛性系桿連接，以避免第二榀剛架的風荷載通過屋面水平支撐也傳遞給邊榀剛架。

3 結語

本文以實際工程為例，探討了高大抗風柱設計的三種方案，方案一雖然是低矮門式剛架中常見的設計方式，但是應用于高大抗風柱時，材料使用較多。而且同方案二一樣，需要進行結構整體屈曲分析。方案二，材料使用較為節省，節點處理也較為方便，但是需要仔細的結構整體屈曲分析。由于結構整體屈曲分析對于設計人員的經驗和理論理解要求較高，方案一和方案二只有在某些特定的環境下采用。方案三是此類結構的最優方案，但是節點設計需要設計人員特別注意。