基于非參數核密度估計法的車輛大數據服役載荷外推方法

于佳偉 鄭松林 趙禮輝 井 清

1. 上海機動車檢測認證技術研究中心有限公司，上海，201805 2. 上海理工大學機械工程學院，上海，200093 3. 上汽集團商用車技術中心，上海，200438

0 引言

對汽車產品而言，高耐久性里程與高可靠性指標要求是保證車輛產品品質的基本前提[1]。在車輛產品耐久性與可靠性評價中，試驗規范尤為重要。一套合理的試驗規范既可有效保證產品的用戶使用可靠度，又有益于產品的輕量化設計。

在車輛產品耐久性試驗規范制定方法方面，已有文獻對此展開了相關研究，例如，結合定遠試驗場實車載荷譜采集和有限元分析方法制定鋼板彈簧的加速壽命試驗程序載荷譜[2]；基于襄樊試車場實測載荷譜制定車身[3]和后橋[4]疲勞試驗的程序載荷譜；以及由汽車控制臂實測載荷譜轉化為臺架疲勞試驗譜[5-6]等。現有文獻中關于道路載荷譜向臺架試驗載荷譜的當量等效轉化方法的研究較多，為耐久性試驗規范的制定提供了參考。

對車輛服役載荷特征的充分研究是制定耐久性試驗規范的關鍵。若試驗規范制定的數據依據僅是汽車試驗場載荷譜，可能導致產品在試驗驗證階段無法完全暴露潛在的用戶使用過程中的失效模式。為了使試驗規范能夠完全反映用戶實際使用情況，有必要對車輛用戶道路的服役載荷特征展開研究。張祿[7]基于參數法概率密度估計，研究了某大型營運客車在用戶道路載荷條件下軸頭和質心三向加速度幅值、前懸穩定桿扭轉和平衡梁彎曲應變幅值的概率密度分布。趙禮輝等[8]基于參數法概率密度估計，建立了用戶使用條件下輕型商用車年行駛里程、行駛車速和載重等的概率密度分布模型。

在用戶實際使用過程中，車輛承受的載荷環境復雜多變，通常難以用固定形式的概率密度分布函數對載荷的分布進行擬合，導致參數法概率密度估計應用的局限性。非參數法概率密度估計不需要假設變量的分布函數形式，概率密度估計結果完全由樣本數據自身的分布決定，能夠靈活準確地得到變量的概率密度估計結果，可有效解決分布形式復雜的隨機變量的概率密度估計問題[9]。

非參數法概率密度估計在諸多領域的機械承載結構載荷特征研究中得到了應用。例如，在軌道交通方面，金新燦等[10]以高速動車組動車輪軸動應力線路實測數據為依據，采用非參數核密度估計法對實測高速輪軸載荷譜進行了擬合外推分析；李凡松等[11]利用非參數二維核密度估計法，提出了多載荷時間歷程輸入條件下的車下設備承載結構疲勞試驗載荷譜編制方法。在工程機械方面，高天宇等[12]基于非參數核密度估計法建立了裝載機轉斗液壓缸鏟掘階段八級程序載荷譜。此外，在農業機械方面，宋清椿等[13]以田間作業動力機械車架為研究對象，采用非參數核密度估計法對車架載荷進行非參數雨流外推，并基于外推結果進行了疲勞壽命預測。

道路車輛承載結構載荷譜因路面特征和駕駛員操作行為不同等因素影響而呈現出較強的隨機性，載荷分布特征差異較大，通常不服從特定的分布函數形式，因此有必要采用非參數概率密度估計方法研究道路車輛承載結構隨機載荷譜的統計分布特征。考慮到車輛服役載荷特征的研究對車輛產品耐久性和可靠性試驗規范制定工作的重要性，本文以某型寬體輕客服役載荷特征的全國大范圍用戶使用習慣數據調研和道路載荷譜采集為數據研究基礎，運用非參數核密度估計統計學方法結合蒙特卡羅仿真方法，研究用戶使用習慣特征的統計方法和車輛服役載荷的外推方法，提出了一套基于用戶使用習慣關聯的車輛服役載荷的外推方法與流程，構建了該車型減振彈簧應變的全壽命周期服役載荷譜。

1 用戶使用習慣特征統計與分析

1.1 非參數一維核密度概率密度估計方法

概率密度估計方法分為參數法和非參數法。由于非參數法不需設定分布函數的具體形式，概率密度估計結果完全由樣本數據自身的分布決定，相比參數法能給出較為準確的密度估計結果。考慮到不同用戶使用習慣之間的差異較大，致使用戶使用習慣特征的分布不遵循固定的形式，因此本文采用非參數核密度估計法統計用戶使用習慣特征。

一維核密度估計法的原理如下：設xi(i=1,2，…，n)是從一維總體X中抽出的獨立同分布的樣本數據，X具有未知的密度函數f(x)，如果存在(-1,1]上的均勻密度函數K(u)≥0且滿足

則f(x)的核密度估計為

式中，K(·)為核函數；h為帶寬；n為樣本容量。

式中，f為真實密度函數，f″表示函數f的二階導數。

我們的內分泌功能受到復雜調控系統的控制，同時也受人體發育不同時期和生活環境的影響，如果這些影響過大，就會導致內分泌功能紊亂。《黃帝內經》提倡“飲食有節，起居有常，不妄作勞”，要求我們遵循自然規律，合理飲食，按時作息，這是一切養生方法的基礎；同時要有樂觀的生活態度，保持心情舒暢，這樣才能使肝氣條達順暢。

通過求取最小化AMISE，得到最佳帶寬

此時最小化AMISE為

其中,[σKR(K)]4/5項與核函數K有關，因此選擇的最佳核函數K應使[σKR(K)]4/5的值最小。當核函數為以下二次項形式時可使得[σKR(K)]4/5最小：

此即為Epanechnikov核函數。幾種常用核函數如表1所示，相比于矩形核，Epanechnikov核和高斯核能夠獲得更為光滑的概率密度估計結果。

表1 幾種常用核函數

1.2 用戶使用習慣典型特征統計與分析

采用非參數一維核密度估計法研究用戶使用習慣特征。首先以年行駛里程為例，研究用戶年行駛里程調研結果的統計分布特征。年行駛里程通過查詢用戶車輛儀表盤里程(km)除以當前車齡(年)計算得到。統計結果的直方圖概率密度估計如圖1所示。基于參數法概率密度估計結合極大似然估計方法，得到幾種常用連續型分布函數的概率密度擬合結果如圖1所示，對數正態分布對樣本數據的擬合效果最好，但仍然與實際樣本數據的分布存在一定的誤差，因此，基于非參數一維核密度估計法，應用高斯核和Epanechnikov核分別對實測樣本數據進行密度估計，兩種核函數密度估計結果基本相同，并與實際樣本數據的分布十分吻合，明顯優于對數正態分布，如圖2所示。

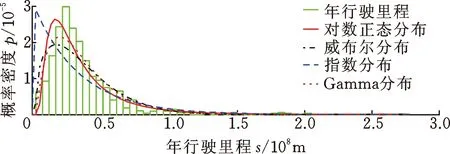
圖1 幾種常用連續型分布的概率密度估計

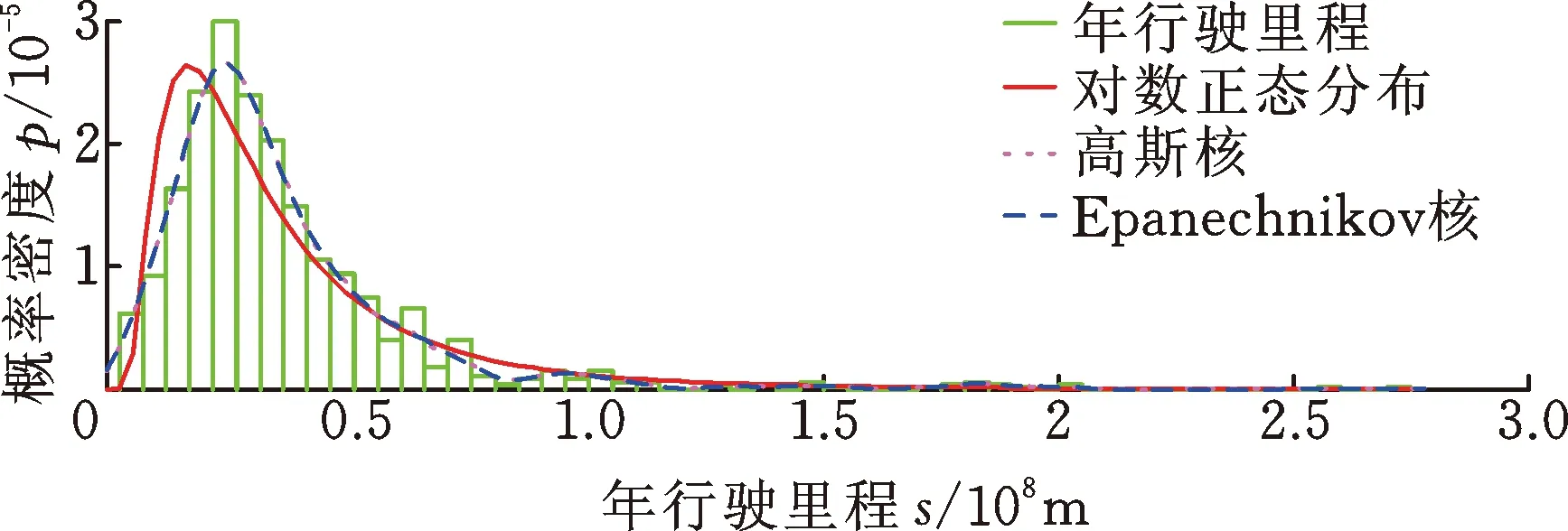
圖2 非參數一維核密度估計

對于本文重點關注的90%分位用戶年行駛里程，采用高斯核和Epanechnikov核密度估計法得到90%分位用戶年行駛里程分別為61 900 km和61 978 km。鑒于兩種核密度估計結果與實測樣本數據分布較為一致，因此取高斯核和Epanechnikov核密度估計結果的均值作為最終結果，則90%分位用戶年行駛里程估計值為61 939 km。

除年行駛里程外，本文還分別計算了90%分位用戶期望車輛服役里程和不同道路類型的用戶行駛里程比例。分析用戶期望車輛服役里程有助于設定合理的車輛耐久性目標，通過采用相同的統計分析方法與流程，得到90%分位用戶期望服役里程估計值為593 000 km。由于在不同道路條件下車輛所承受的載荷差異較大，為合理構建車輛服役載荷譜，有必要對用戶在不同道路類型下的行駛里程比例進行估計，通過采用相同的統計分析方法與流程，得到90%分位用戶城市道路行駛里程比例、高速公路行駛里程比例、郊區道路行駛里程比例和惡劣道路行駛里程比例估計值分別為40%、33%、23%和4%。經以上統計分析得到的用戶使用習慣特征的90%分位估計值歸納在表2中。

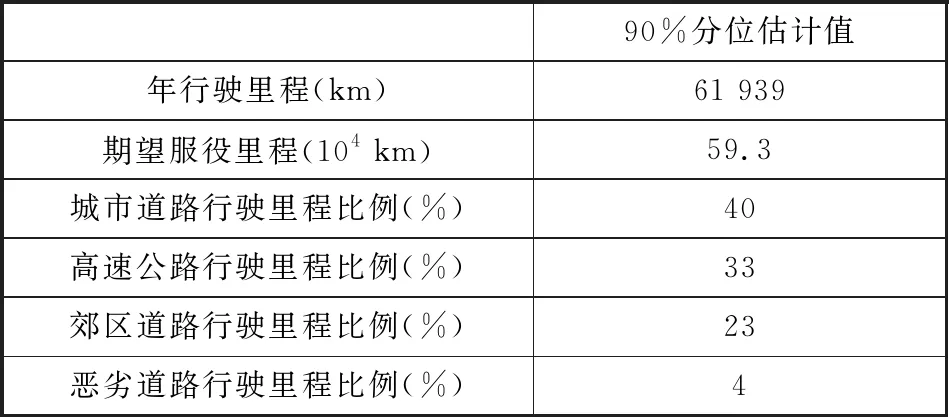
表2 用戶使用習慣特征的90%分位估計值

2 用戶道路大數據載荷譜采集

用戶道路載荷譜采集是掌握用戶道路載荷特征的最直接和有效的方法，同時也為車輛全壽命周期服役載荷譜的建立提供了載荷譜樣本。在全國范圍內對該車型開展了載荷譜采集，采集路線涉及全國21個省，總里程約為18 000 km，其中各道路類型的載荷譜采集里程如表3所示。該客車前懸架為麥弗遜式獨立懸掛，為采集減振器彈簧的道路載荷譜，沿彈簧軸向布置了T型全橋應變片，如圖3所示，測量彈簧的扭轉載荷譜。圖4展示了一段城市道路載荷譜，所采集到的載荷譜為載荷-時間歷程形式，里程約52 km，以左前減振器彈簧應變通道為例。在應用于載荷特征計算之前，對采集到的載荷譜進行了剔除尖峰異常值和糾正漂移等信號預處理工作，保證用于計算分析的載荷譜能夠代表用戶道路的真實載荷環境。

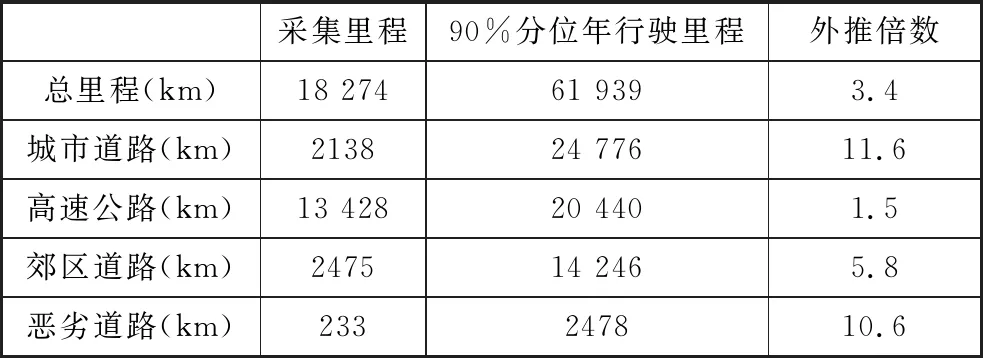
表3 各道路類型載荷譜采集里程和外推倍數

圖3 前減振器彈簧應變片

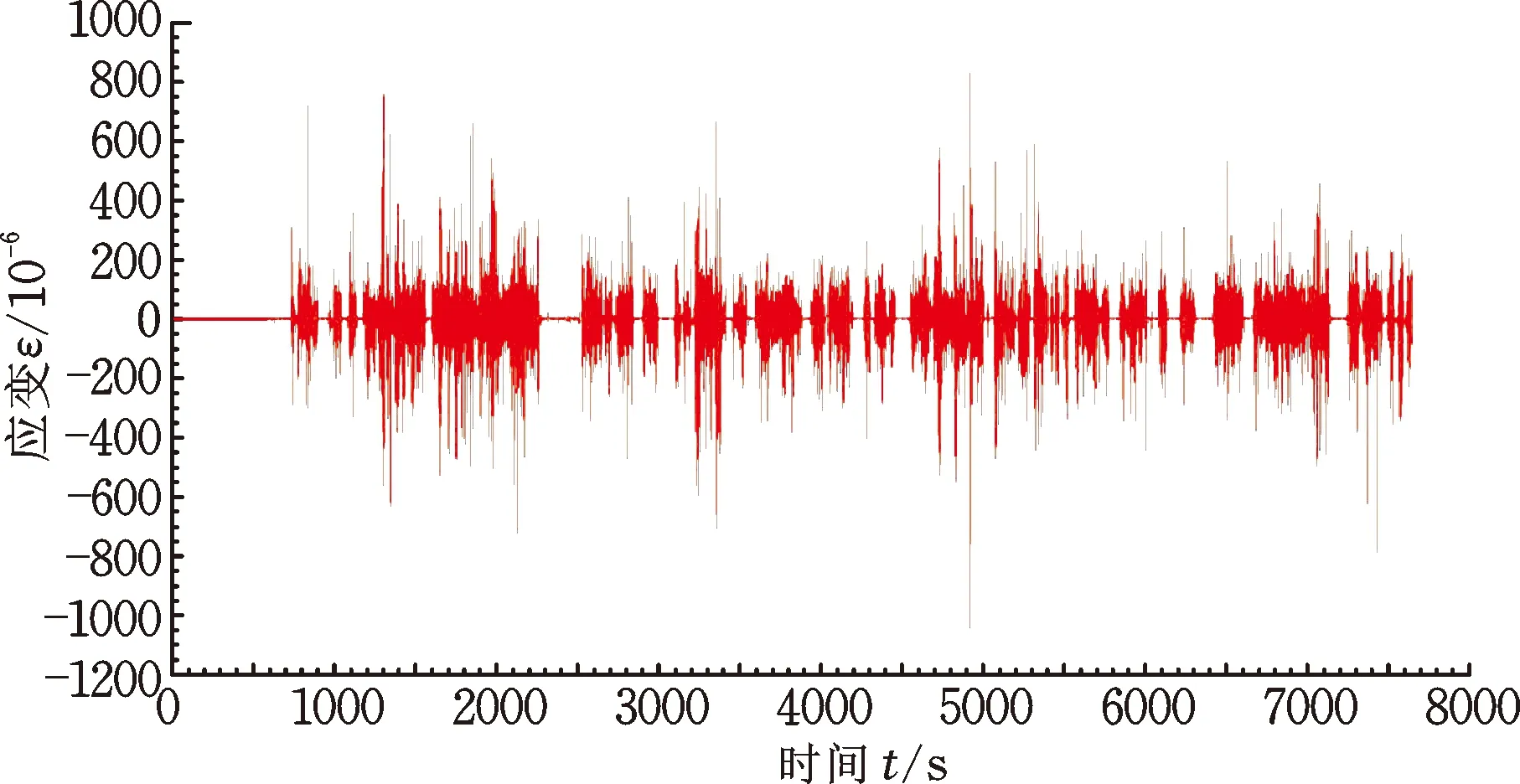
圖4 杭州城市道路載荷譜

3 載荷譜外推方法與流程

建立車輛全壽命周期服役載荷譜是為了合理地制定零部件的疲勞耐久評價試驗規范。對疲勞壽命分析而言，載荷的幅值域特征被認為是影響疲勞壽命的主要因素。雨流循環計數法屬于雙參數循環計數法，記錄了載荷循環的二維信息，如起始值和終點值或幅值和均值，與材料的應力-應變遲滯回線相對應，具有較為明確的力學概念。雨流循環計數法通過對載荷-時間歷程進行循環計數，可獲得載荷均幅值與其作用次數間的對應關系，因而被認為是目前預測疲勞壽命較好的方法。此外，由于雨流循環矩陣包含詳細的載荷循環的均幅值信息，有利于轉換為疲勞耐久試驗規范，因此本文采用非參數二維核密度估計法對用戶道路實測載荷譜的雨流矩陣展開外推，建立該車型的全壽命周期服役載荷譜。

3.1 非參數二維核密度估計法

一維核密度估計法適用于一維隨機變量的概率密度估計問題，而對于二維乃至多維隨機變量的概率密度估計問題，則需要采用多維核密度估計法。多維核密度估計法和一維核密度估計法的基本原理相同。多維核密度估計法的通用表達形式為

式中，X為多維數據總體;Xi為觀測到的第i個多維數據樣本；H為非奇異d×d帶寬矩陣；Kd為d維概率密度函數。

對于二維核密度估計，常用的兩種核函數類型為二維正態密度函數和二維Epanechnikov核函數。二維正態密度函數表達式為

式中，x和y分別代表了二維數據的兩個維度。

二維Epanechnikov核函數表達式為

若帶寬矩陣H按H=hA的形式取值，且A取為單位矩陣，則二維核密度估計法可表示為

(10)

式中，xi和yi表示從二維數據總體中抽取的兩個維度的樣本數據。

3.2 用戶道路載荷外推流程

載荷外推需明確兩個關鍵內容，即載荷數據對象和外推目標里程。載荷數據對象選為用戶道路實測載荷譜，考慮到不同道路類型的載荷環境差異較大，本文按照不同道路類型分別展開外推。為避免外推倍數過大，同時考慮以年為周期對車輛服役載荷進行劃分較為合理，因此選擇年行駛里程作為外推目標里程。本文提出的用戶道路載荷外推流程如圖5所示，共有兩處采用非參數核密度估計法，其中用戶使用習慣典型特征的數據為一維隨機變量，采用一維核密度估計法研究其分布特征；而用戶道路載荷譜雨流矩陣的數據形式為二維隨機變量(載荷起始點和終止點)，因此采用二維核密度估計法對其進行概率密度估計。載荷外推倍數由各道路類型的年行駛里程統計值除以實測載荷譜里程得到，如表3所示。將外推后各道路類型的載荷疊加，得到年行駛里程用戶載荷。最后，按照用戶期望服役里程與年行駛里程間的倍數，以年行駛里程用戶載荷為基本單位進行載荷疊加，構建車輛全壽命周期服役載荷譜。

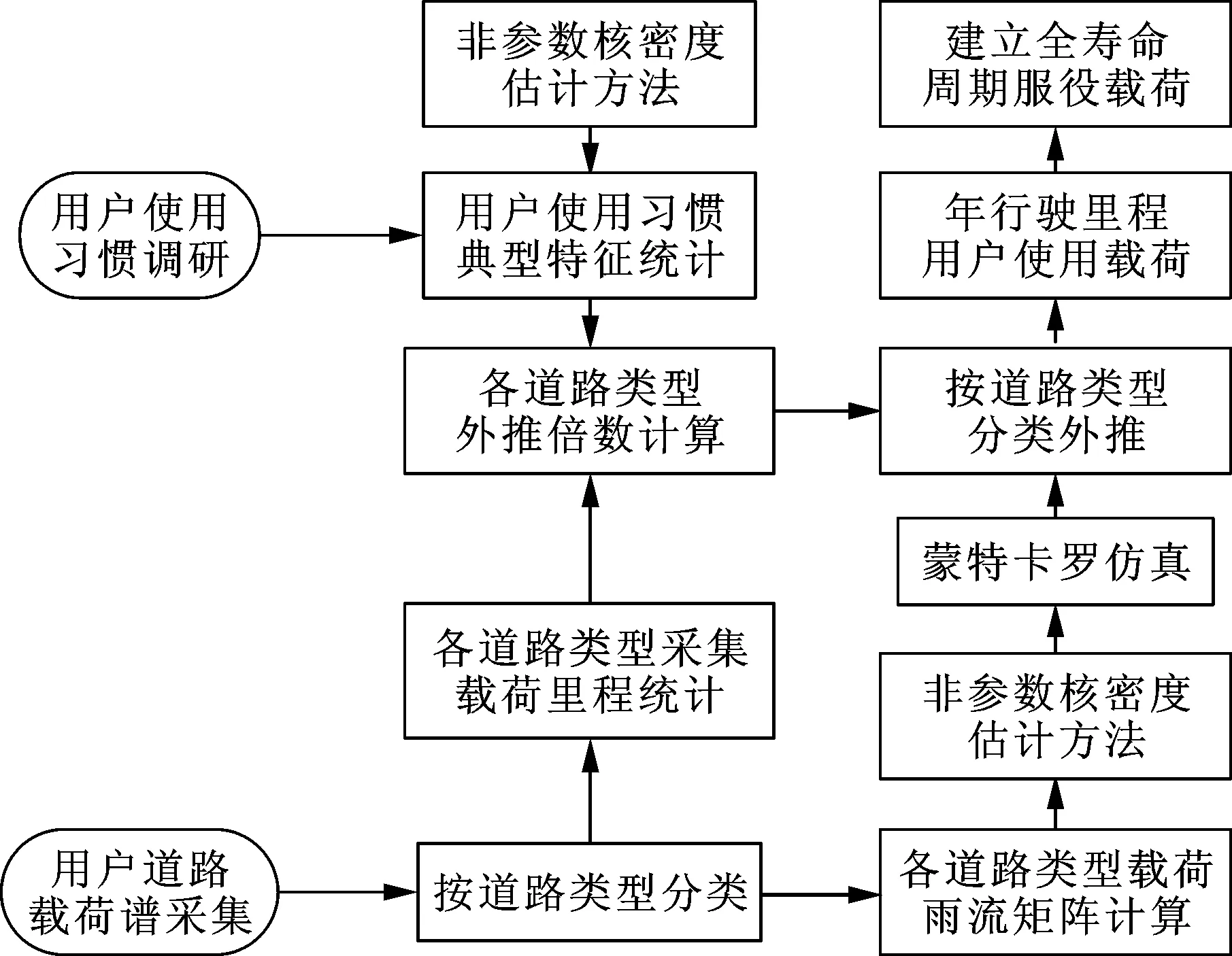
圖5 用戶道路載荷外推流程

4 車輛全壽命周期服役載荷譜構建

依據圖5的流程，本文將以道路類型分類進行載荷外推，由于篇幅所限，以郊區道路載荷譜為例，詳細闡述載荷外推的過程。

4.1 載荷譜雨流矩陣計算

首先對采集的載荷譜按道路類型分類，統計每段載荷譜的載荷最大值和最小值，確定合理的雨流矩陣坐標界限。之后逐一計算每段載荷譜的雨流矩陣。為便于對雨流矩陣進行概率密度估計，雨流矩陣采用from-to的形式表示，且刪除了載荷變程為最大變程5%以下的低幅值載荷，這些低幅值載荷的循環數目所占比例大，且對結構件造成的損傷幾乎可以忽略。將郊區道路所屬載荷譜的雨流矩陣進行疊加，得到郊區道路實測總載荷的雨流矩陣如圖6所示，圖中橫坐標表示載荷的起始點，縱坐標表示載荷的終止點，而最右側的標識圖表示雨流矩陣中各單元載荷的重復次數。從圖6中可知，矩陣副對角線上的小變程載荷已被刪除，矩陣主對角線上顯示存在個別大變程載荷。

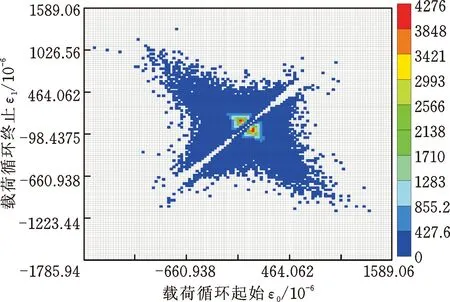
圖6 郊區道路實測總載荷的雨流矩陣

4.2 雨流矩陣概率密度估計和里程外推

運用非參數二維核密度估計法，分別采用Epanechnikov核和高斯核對郊區道路總載荷雨流矩陣進行概率密度估計，結果如圖7所示。兩種核密度估計結果在分布形態上大體一致，但高斯核在大變程載荷區域(矩陣主對角線兩端)內的概率密度估計范圍比Epanechnikov核略廣，分布形態更飽滿。基于這兩種核密度估計結果，結合蒙特卡羅仿真方法，按表3中郊區道路里程外推5.8倍，兩種核密度估計法第一次載荷里程外推結果如圖8所示。兩種方法外推后載荷的分布形態較為一致，均極大地豐富了原實測載荷的分布區域。

(a) Epanechnikov核

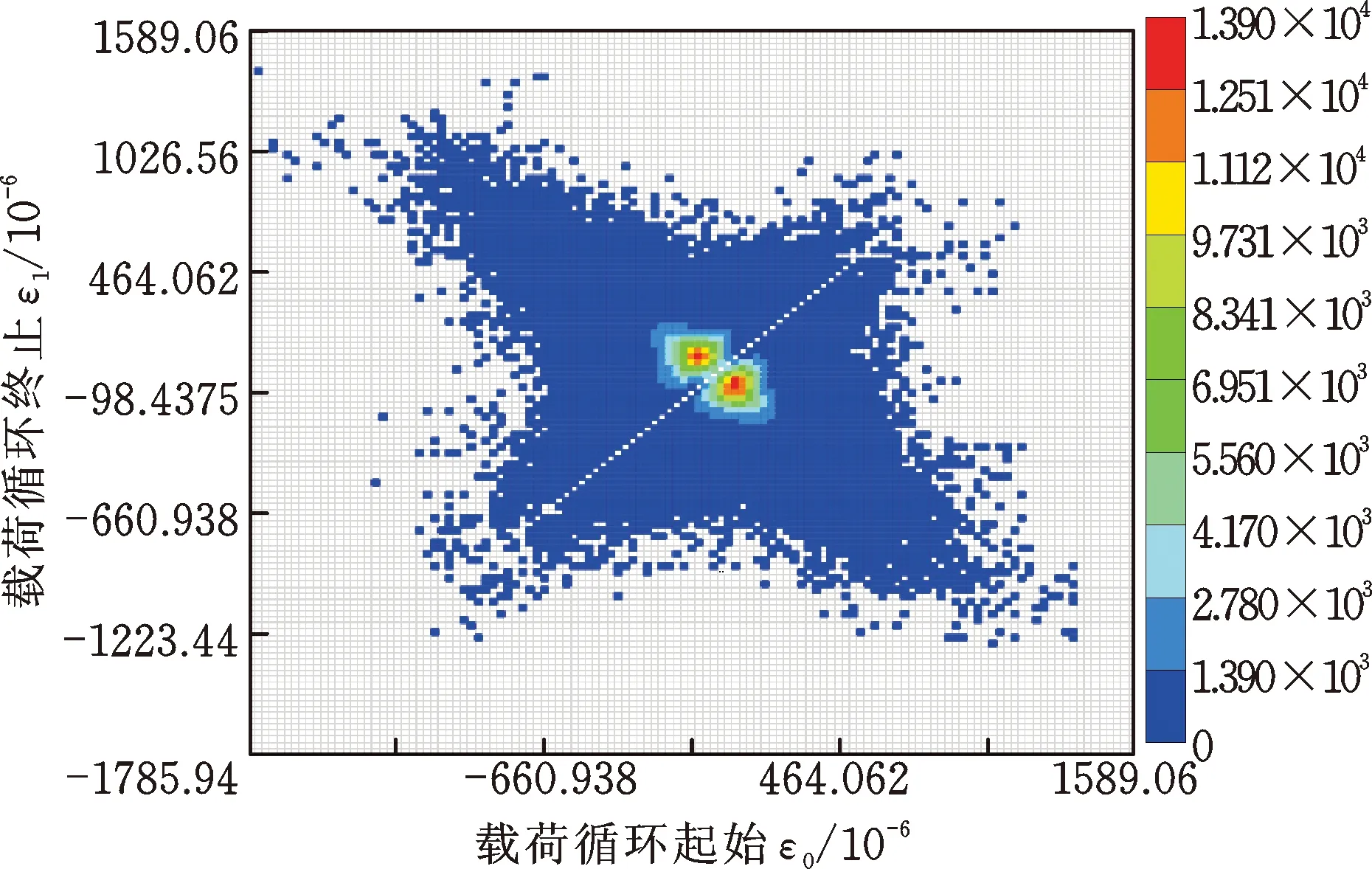
(a) Epanechnikov核

4.3 多次外推過程的一致性分析

基于載荷雨流矩陣的概率密度估計結果，結合蒙特卡羅仿真方法進行載荷里程外推。在載荷里程外推過程中，每個載荷循環按所估計的雨流矩陣分布概率隨機地分配到雨流矩陣中的不同位置，因此外推的結果不是唯一的。為了研究外推結果的可能性，本文基于Epanechnikov核和高斯核的概率密度估計結果分別進行了20次載荷外推仿真。兩種核密度估計法多次外推仿真結果的累計循環計數如圖9所示，可見多次外推結果的載荷變程的分布基本一致，并且較好地保留了原載荷變程的分布趨勢。

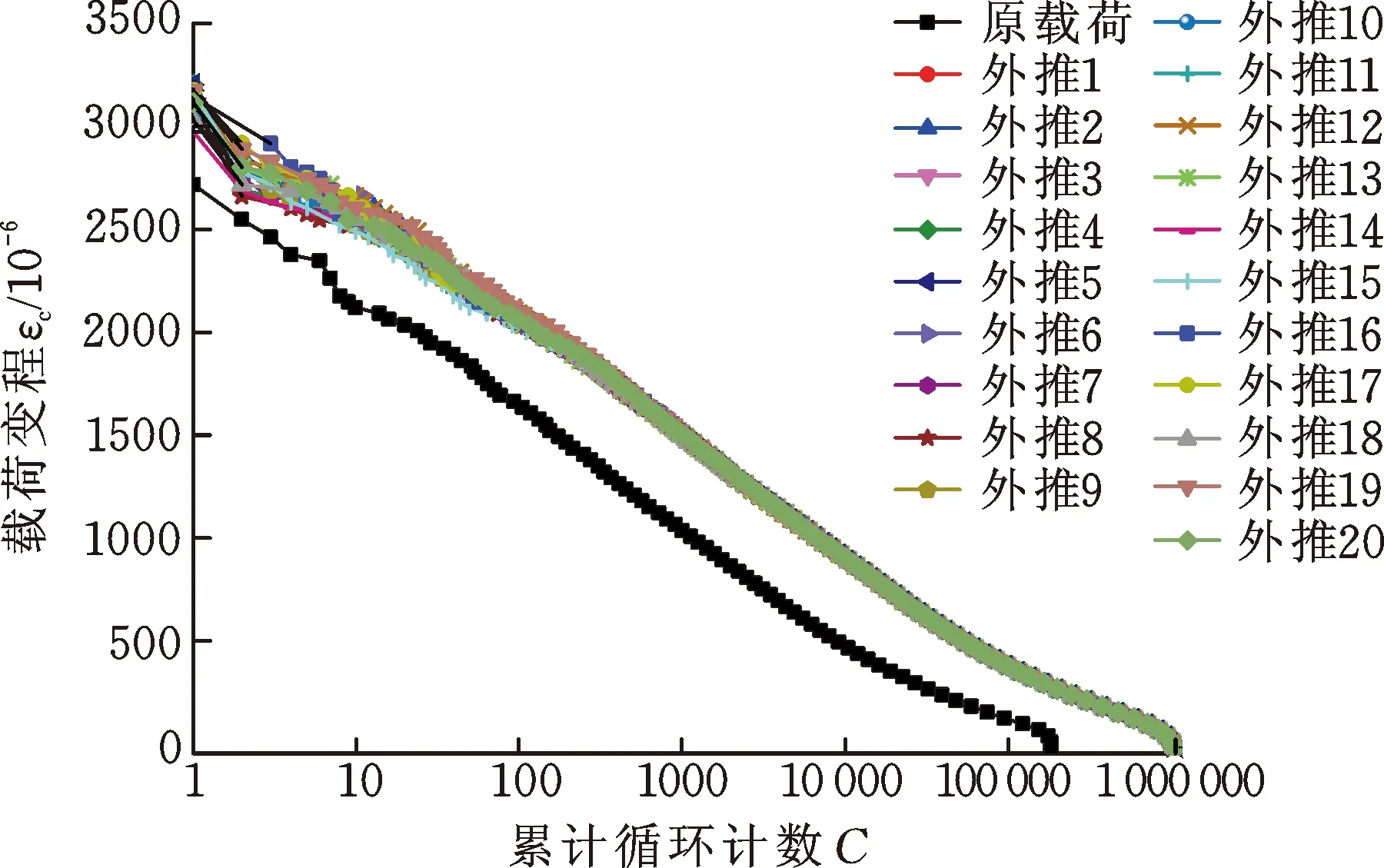
(a) Epanechnikov核

此外，計算了外推后載荷的最大變程和總偽損傷相對原載荷的增大倍數，載荷偽損傷的計算參照文獻[14]中所述的方法,兩種核密度估計法多次外推仿真結果的載荷最大變程和總偽損傷變化倍數如圖10所示。對于載荷最大變程，兩種方法多次外推結果的一致性較好，均保持在原載荷最大變程的1.1～1.2倍之間；對于載荷總偽損傷，基于高斯核的多次外推結果保持在原載荷的6.2倍左右，而基于Epanechnikov核的多次外推結果保持在原載荷的6.0倍左右。基于高斯核外推后載荷的總偽損傷略大于基于Epanechnikov核外推后載荷的總偽損傷，這是由于高斯核在大變程載荷區域(矩陣主對角線兩端)內的概率密度估計范圍比Epanechnikov核略廣，分布形態的估計也更為飽滿。但兩種方法各自多次外推后載荷總偽損傷的一致性較好。以上分析結果表明兩種核密度估計法的多次外推后載荷的幅值、分布和損傷的一致性均較好。對于這兩種核密度估計法，各自多次外推后載荷間的差異很小。

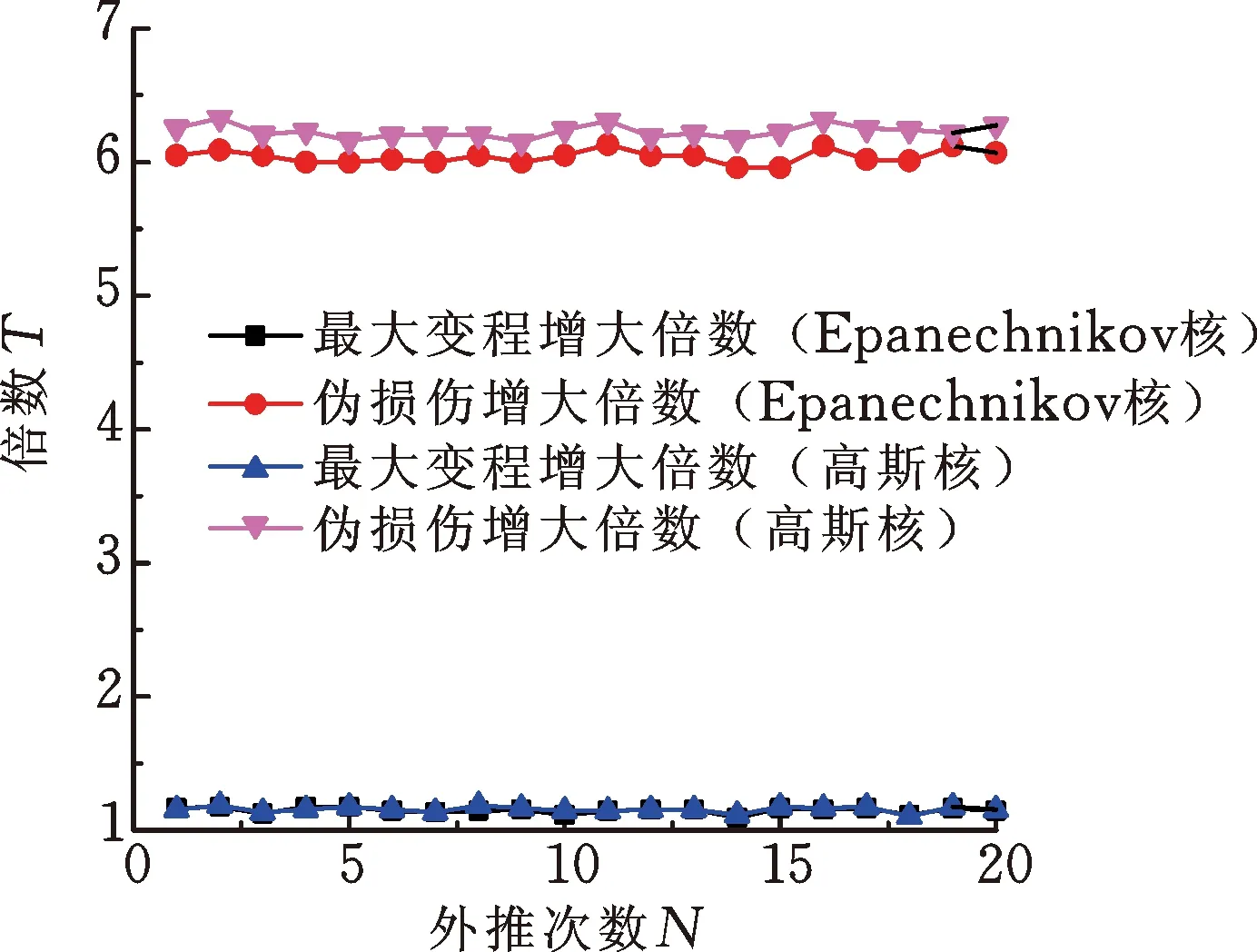
圖10 多次載荷外推結果的載荷最大變程和總偽損傷變化

4.4 車輛全壽命周期服役載荷的建立

考慮到兩種核密度估計法多次載荷外推結果的一致性較好，且基于高斯核外推后載荷的總偽損傷略大于基于Epanechnikov核外推后載荷的總偽損傷，從車輛產品耐久性驗證的保守性考慮，選擇基于高斯核外推后載荷總偽損傷最大的一次外推結果(具體為第2次外推，偽損傷為原載荷的6.33倍)作為郊區道路年行駛里程載荷。其他道路類型年行駛里程載荷的建立采取與郊區道路相同的方法進行，最后將各道路類型外推后年行駛里程載荷的雨流矩陣進行疊加，得到外推后年行駛里程總載荷的雨流矩陣如圖11所示，原實測載荷譜的總雨流矩陣如圖12所示，可見，外推后總載荷在保持原實測載荷分布趨勢的條件下，極大地豐富了原實測載荷，使得總載荷的變化范圍更廣，載荷分布形態也更加飽滿，并且未引入極端載荷。圖11和圖12中色標的最大值(9.112×104和2.996×104)表示雨流矩陣中某一單元載荷的最大重復次數。外推倍數為3.4倍，外推的過程實質上是將雨流矩陣中的載荷單元依據概率密度分布和外推倍數隨機分配的過程，因此外推后雨流矩陣中所有載荷單元的重復次數之和為外推前的3.4倍，但每個載荷單元的最大重復次數不一定為3.4倍，如圖11和圖12雨流矩陣中載荷重復次數最大的單元，外推后其次數擴大了近3倍。外推后年行駛里程總載荷的偽損傷為原實測載荷偽損傷的5.41倍，而里程外推的倍數為3.4倍，從損傷倍數的變化也說明了外推后的總載荷極大地豐富了原實測載荷的變化范圍。依據表2中用戶期望服役里程與年行駛里程之間的倍數關系，以車輛年行駛里程載荷作為一個耐久循環周期，將圖11中所構建的年行駛里程載荷雨流矩陣按照倍數關系線性疊加，即可得到該車型前減振器彈簧應變的全壽命周期載荷。全壽命周期載荷的建立可為后續結構件疲勞壽命的仿真計算和臺架試驗規范的制定工作提供充足的載荷數據依據。

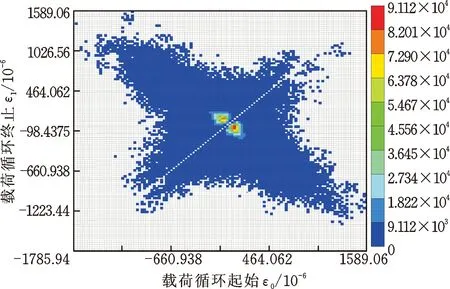
圖11 外推至年行駛里程的所有道路載荷雨流矩陣

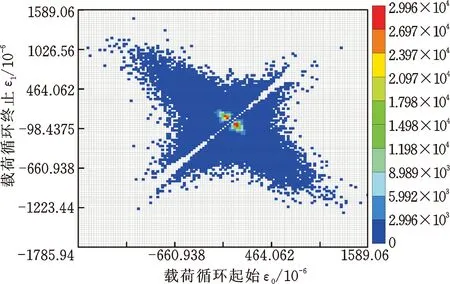
圖12 所有道路實測總載荷的雨流矩陣

5 結論

(1)非參數核密度估計法較之參數法能夠更準確地描述實際樣本數據的分布特征，能夠更真實地反映用戶使用習慣典型特征的真實值。

(2)提出了車輛全壽命周期服役載荷的外推方法與流程。以年行駛里程為耐久循環周期，采用非參數二維Epanechnikov核和高斯核密度估計法，結合蒙特卡羅仿真，分別對實測載荷譜的雨流矩陣開展了載荷里程外推。

(3)基于Epanechnikov核和高斯核的概率密度估計結果分別進行了多次載荷外推仿真。多次外推結果的載荷變程的分布基本一致，并且較好地保留了原載荷變程的分布趨勢。兩種方法各自多次外推后載荷最大變程和總偽損傷的一致性較好。對于這兩種核密度估計法，各自多次外推后載荷間的差異很小。

(4)基于高斯核外推后載荷的總偽損傷略大于基于Epanechnikov核外推后載荷的總偽損傷，這是由于高斯核在大變程載荷區域內的概率密度估計范圍比Epanechnikov核略廣，分布形態的估計更為飽滿，致使外推后大變程載荷區域內的載荷循環數目更豐富，總偽損傷也略大。

(5)考慮到基于高斯核密度估計法外推后載荷更為保守，采用高斯核密度估計法構建了該車型前減振器彈簧應變的年行駛里程載荷雨流矩陣。外推后總載荷在保持原實測載荷分布趨勢的條件下，極大地豐富了原實測載荷，使得總載荷的變化范圍更廣，載荷分布形態更飽滿，并且未引入極端載荷。