基于ADAMS的6PSS并聯機構多目標優化研究*
鄭江濤,田大鵬*,高志良
(1.中國科學院 長春光學精密機械與物理研究所,吉林 長春 130033; 2.中國科學院大學,北京 100049)
0 引 言
并聯機構具有結構緊湊、剛度高、動態響應快等優點,在先進制造裝備、生物醫學裝置、航空航天運動模擬等領域的應用已取得了巨大的成功[1-3]。然而,并聯機構的性能與它的結構參數密切相關,當其結構參數選擇不太合適時,并聯機構的運動性能可能會很差。
因此,許多研究者一直致力于并聯機構性能的優化研究。最常用的優化方法大致可以分為兩類:(1)基于目標函數的優化方法;(2)基于性能圖譜的優化方法。
目標函數法的原理是:首先,根據優化指標建立目標函數和約束條件;然后,使用算法搜索優化結果。文獻[4]采用了窮盡搜索最小化算法,將并聯機構可操作性和工作空間大小的度量結合起來,并通過運動學優化過程得出了可操作性和空間利用率之間的最佳折衷設計。文獻[5]在考慮了關節限制和連桿干涉的約束條件下,采用隨機搜索算法對Delta機器人和Gough-Stewart平臺進行了優化,找到了使有效規則工作空間最大化的機械手幾何結構。文獻[6]以運動學雅克比矩陣的條件數和可操作度作為目標函數,采用了多目標進化算法NSGA-II對六自由度運動模擬平臺進行了優化。文獻[7]以雅可比矩陣的性能指標條件數、剛度、速度極值作為目標函數,采用了罰函數法處理約束條件,提出了性能分類的方式作為多目標優化的準則,最后利用遺傳算法進行了參數優化。
該方法多用于參數變量較多,且目標函數過于復雜的情況。
基于性能圖譜的優化設計方法的關鍵是:在一個有限的區域內表達出機構的性能與尺寸的關系,進而得到機構的性能圖譜。文獻[8]利用這種方法對3PRS機構和二自由度球面5R并聯機構進行了優化,使其在工作空間內有較好的運動和力傳遞性能。文獻[9]建立了3-RUU微動并聯機構的尺寸型模型,并根據尺寸型模型及定義的性能指標繪制了反映機構性能與尺寸參數關系的性能圖譜。文獻[10]采用了綜合性能圖譜法結合主成分分析法,對5-PSS/UPU并聯機構進行了多目標優化。
該方法可以在一個有限的設計空間內直觀地表達出設計指標和相關設計參數的關系,但存在的最大問題是:當需要優化的特征參數較多時,不能在一個有限的空間中完整地表示出其性能圖譜。
以上兩種優化方式,都存在比較繁瑣、復雜的特點。為找到一種更容易、更快速的優化方法,研究人員利用ADAMS、Isight等軟件集成的先進優化算法。該方法實際上也是一種基于目標函數的優化方法,但其操作方便,更為便捷和直觀。如文獻[11]基于ADAMS對空間光學遙感器6自由度定位器的結構進行了單目標的優化設計。文獻[12]采用了虛擬樣機技術,對6SPS并聯機構的驅動力進行了單目標的優化。
本文采用基于ADAMS的多目標優化設計方法,研究設計變量的變化對目標函數的影響,而且利用ADAMS集成的優化算法,對6PSS并聯機構的承載能力和運動范圍進行優化,為6PSS并聯機構的結構設計和進一步的研究奠定基礎。
1 參數化模型的建立
1.1 設計變量創建
6PSS并聯機構的構型如圖1所示。
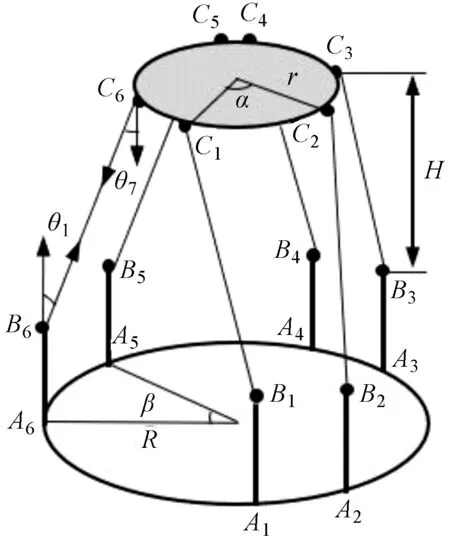
圖1 6PSS并聯機構示意圖
由圖1可知:就此機構而言,需要進行優化設計的結構參數有:動平臺球鉸幾何中心分布的半徑r、定平臺球鉸幾何中心分布的半徑R、動平臺球鉸長邊對應的圓心角α、定平臺球鉸短邊對應的圓心角β、初始高度H(動平臺球鉸中心點所在的平面和定平臺球鉸中心點所在的平面之間的距離)。
因此,6PSS并聯機構的設計變量寫成矢量的形式為:
x=(x1,x2,x3,x4,x5)T=(r,R,α,β,H)T
其中,各設計變量之間相互獨立,各分量的物理意義如表1所示。

表1 設計變量的物理意義及單位
根據6PSS并聯機構的實際操作空間、機械結構的約束要求,以及避免發生奇異性的要求,定平臺和動平臺所對應的球鉸分布不能相似,所以各個設計變量的取值范圍為:
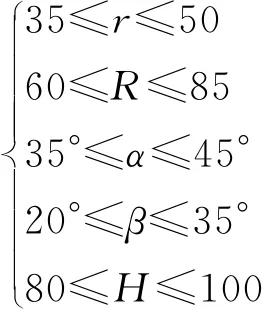
1.2 參數化模型創建
本文采用參數化關鍵點坐標的方法,建立6PSS并聯機構的參數化模型[13]。參數化點的坐標如表2所示。

表2 參數化點的坐標
創建完參數化點后,需要再根據圖1創建相應的構件,然后添加相應的運動副。
為了不失一般性,筆者首先在動平臺質心處加一點驅動,六自由度方向同時加載正弦位移/轉角驅動函數,沿x、y、z方向的位移函數設置為2sin(2πt),繞x、y、z軸旋轉的驅動函數為2dsin(2πt);利用ADAMS模型的運動學逆解仿真結果得到移動副1~6對應的樣條函數,即SPLINE_1-SPLINE_6;然后去除ADAMS模型的動平臺質心的點驅動,在每個移動副關節處加上平移驅動MOTION_1-MOTION_6,設定驅動函數為AKISPL(time,0,SPLINE_1,0),…,AKISPL(time,0,SPLINE_6,0);最后在動平臺的質心處添加外部載荷,力的大小F=10 N,方向豎直向下,力矩大小T=10 N·m,方向豎直向下。
完成以上工作后,所創建的6PSS并聯機構的參數化模型如圖2所示。
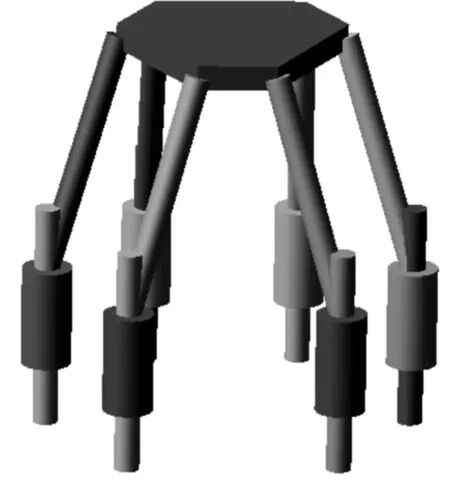
圖2 6PSS并聯機構的參數模型
1.3 目標函數創建
對于6PSS并聯機構而言,其要有較高的承載能力和較大的運動范圍,將其轉化為數學模型,即是在動平臺承受相同的負載,且6個驅動副的運動規律相同時,6個驅動副受力的最大值最小,動平臺質心的動坐標系相對于定坐標系x、y、z軸的3個轉動角的最小投影角最大。
在ADAMS中創建兩個測量函數:
Mea_1=max(max(max(Force_1,Force_2),
max(Force_3,Force_4)),max(Force_5,Force_6))
(3)
Mea_2=min(min(ABS(Alpha),ABS(Beta)),
ABS(Gamma))
(4)
式中:Mea_1—每一個運動周期內6個移動副驅動力的最大值;Mea_2—每一個運動周期內動平臺的質心繞定坐標系x、y、z軸的3個轉動角的最小值;Force_i(i=1、2……6)—6個移動副驅動力的測量函數;Alpha,Beta,Gamm—動坐標系相對于定坐標系的x、y、z軸的3個轉動角的測量函數。
在一個周期內,6個移動副的驅動力和動平臺質心的轉角隨時間成正的正弦規律運動,因此,分別取一個周期內的均值作為目標函數。因為要求并聯機構有較高的承載能力和較大的運動范圍,即并聯機構驅動力最小和轉動角最大,此處選擇目標函數分別為:min(f1(x))和max(f2(x));其中,f1(x)、f2(x)可以表示為:
f1(x)=Averageof(Mea_1)=Averageof(max(max(max(Force_1,Force_2),
(5)
max(Force_3,Force_4)),max(Force_5,Force_6)))
f2(x)=Averageof(Mea_2)=Averageof(min(min(ABS(Alpha),ABS(Beta)),ABS(Gamma)))
(6)
1.4 約束函數創建
1.4.1 球面副轉角的限制
6PSS并聯機構共有12個球面副,球面副的轉角范圍是有限制的。
球面副的轉角約束條件可以表示為:
(7)
式中:θi—第i個球面副的基座固結的坐標系的z軸和球面副連接的桿向量li之間的夾角;ni—第i個球面副的基座的z向向量;R—球面副相對于固定坐標系的姿態。
因此,筆者分別建立12個球面副轉角的測量函數,并命名為MEA_ANGLE_i,(i=1,2…12);然后,建立球面副的約束函數MEA_ANGLE_i-30°≤0,(i=1,2…12)。
1.4.2 連桿的干涉
連接上下平臺的連桿是有一定的尺寸大小的;因此,各桿之間可能發生干涉。這里假設各桿都是圓柱狀的,其直徑為D,若Di(i=1,2…6)為兩相鄰中心線之間的最短距離,則兩桿不發生干涉的條件是Di≥D[14]。對于連桿之間的干涉約束,通過在連桿之間添加實體接觸命令,使各個連桿之間不能相互穿透幾何體,從而可以防止發生干涉。
所以,由參數化模型時各個設計變量的約束和球面副轉角的約束,共同組成了6PSS并聯機構的約束條件,即為:
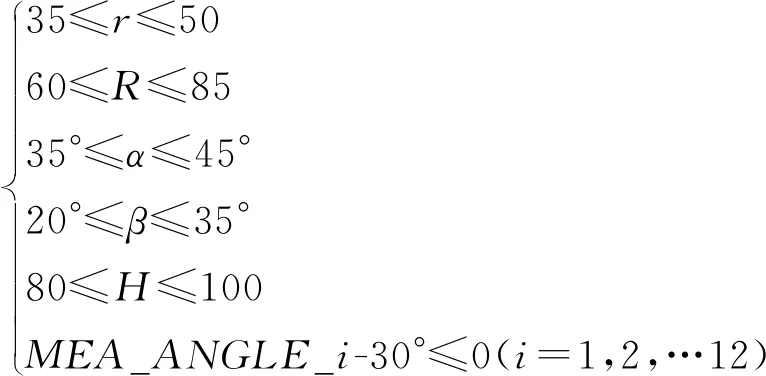
(8)
2 設計變量對目標函數的影響
2.1 動平臺球鉸幾何中心圓的半徑對目標函數的影響
筆者在ADAMS中,研究動平臺球鉸幾何中心圓的半徑對目標函數的影響。目標函數隨動平臺球鉸幾何中心圓的半徑變化曲線,如圖3所示。
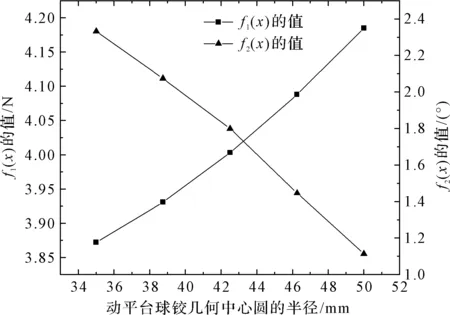
圖3 目標函數隨動平臺球鉸幾何中心圓的半徑變化曲線
從圖3可以看出:目標函數f1(x)的值與動平臺球鉸幾何中心圓的半徑成正相關的關系,目標函數f2(x)的值與動平臺球鉸幾何中心圓的半徑成負相關的關系。
2.2 定平臺球鉸幾何中心圓的半徑對目標函數的影響
筆者在ADAMS中,研究定平臺球鉸幾何中心圓的半徑對目標函數的影響。目標函數隨定平臺球鉸幾何中心圓的半徑變化曲線,如圖4所示。
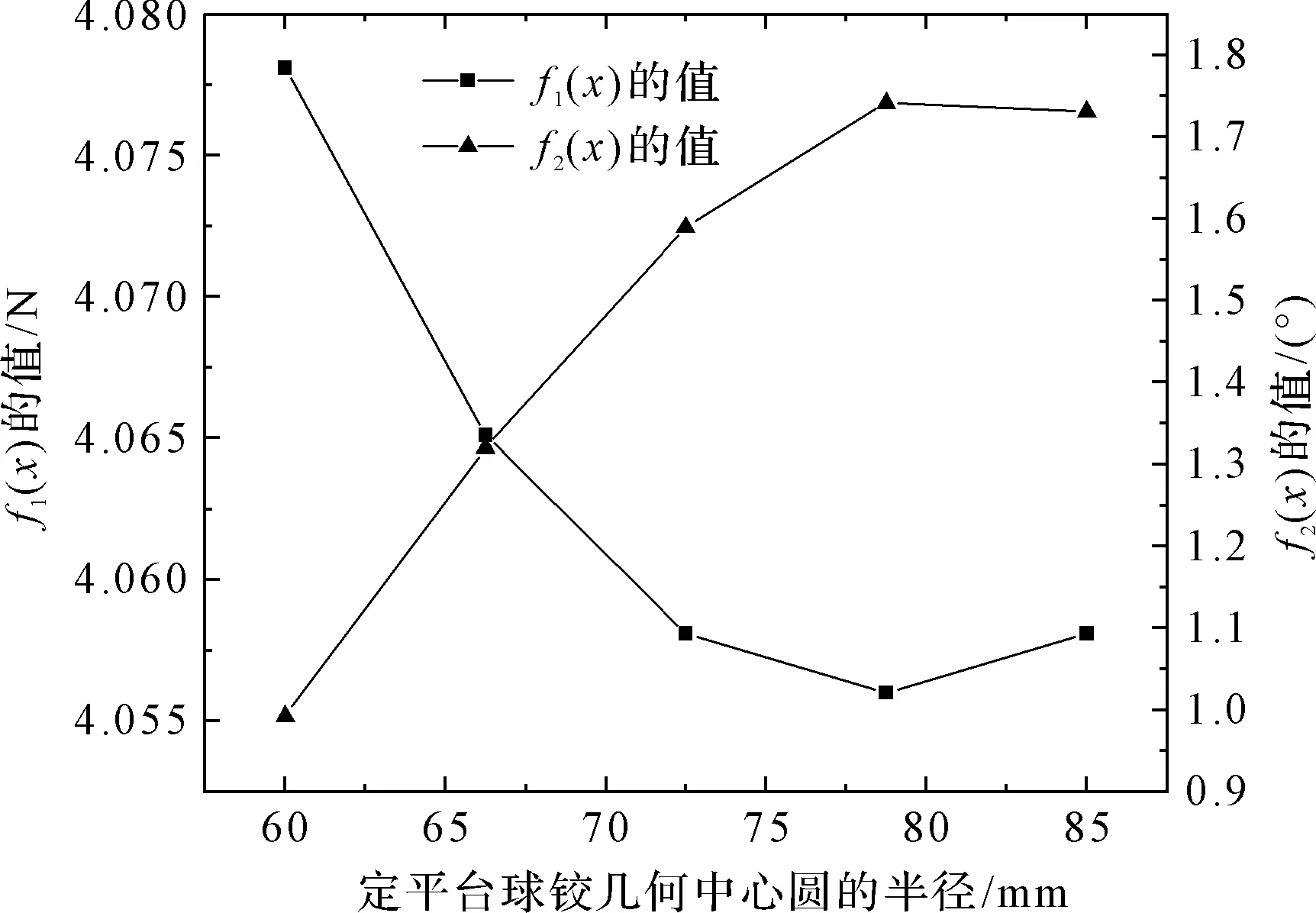
圖4 目標函數隨定平臺球鉸幾何中心圓的半徑變化曲線
從圖4可以看出:目標函數f1(x)的值與定平臺球鉸幾何中心圓的半徑,在一定范圍內成負相關的關系;目標函數f2(x)的值與動平臺球鉸幾何中心圓的半徑,一定范圍內成正相關的關系。
2.3 動平臺球鉸長邊對應的圓心角對目標函數的影響
在ADAMS中研究動平臺球鉸長邊對應的圓心角對目標函數的影響。目標函數隨動平臺球鉸長邊對應的圓心角變化曲線,如圖5所示。
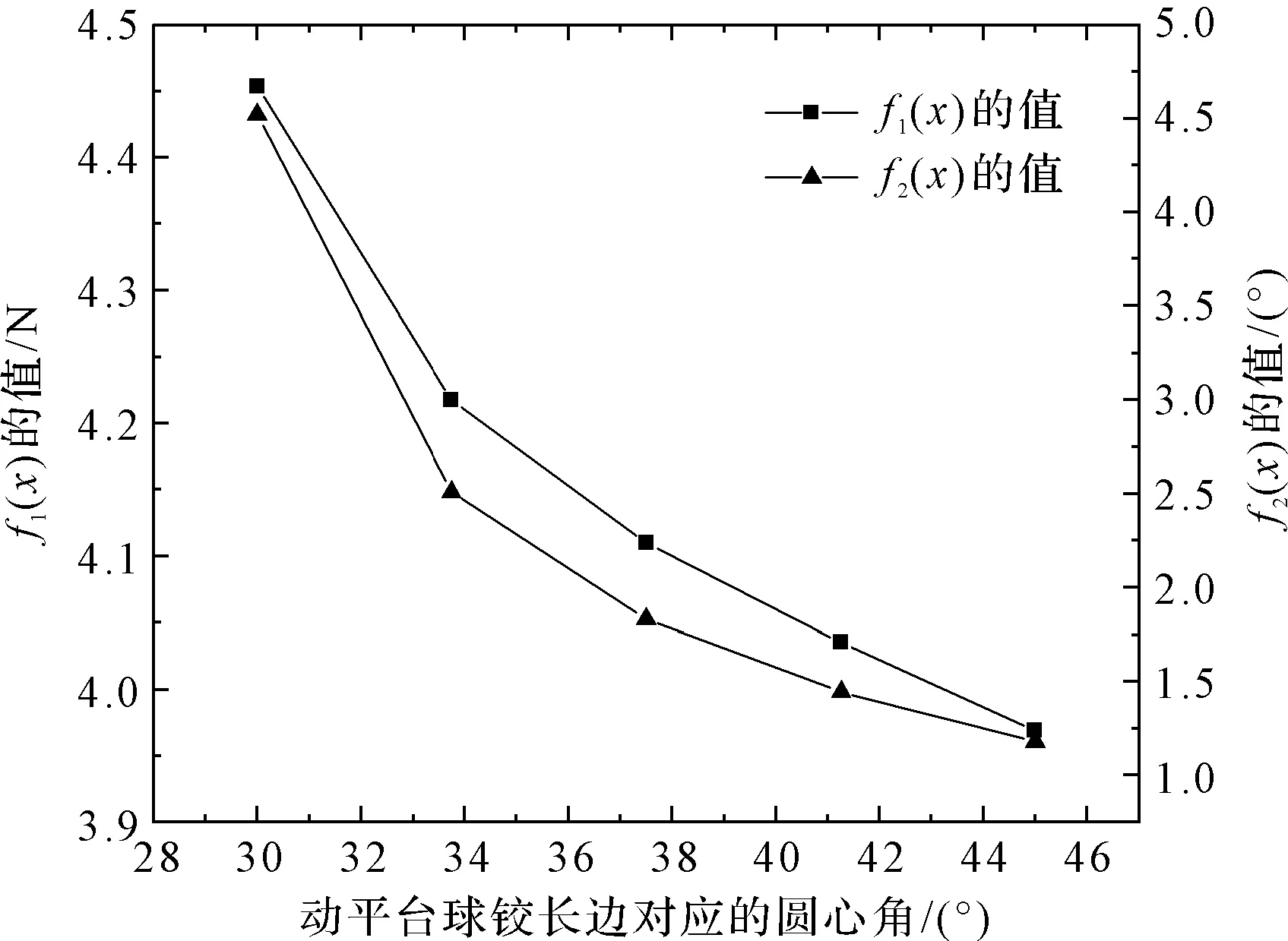
圖5 目標函數隨動平臺球鉸長邊對應的圓心角變化曲線
從圖5可以看出:目標函數f1(x)的值與動平臺球鉸長邊對應的圓心角成負相關的關系,目標函數f2(x)的值與動平臺球鉸長邊對應的圓心角成負相關的關系。
2.4 定平臺球鉸短邊對應的圓心角對目標函數的影響
在ADAMS中研究定平臺球鉸短邊對應的圓心角對目標函數的影響。目標函數隨定平臺球鉸短邊對應的圓心角變化曲線如圖6所示。
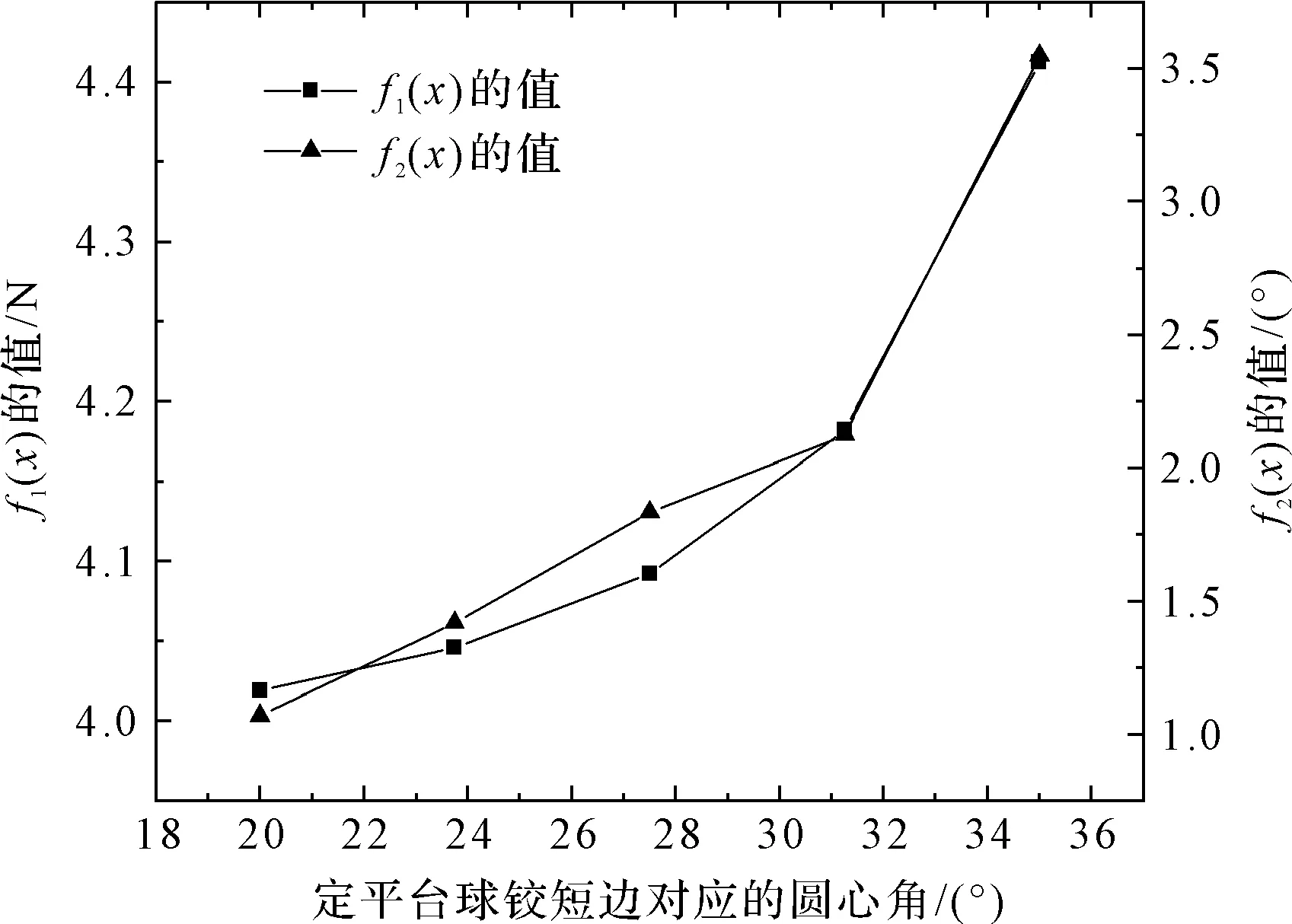
圖6 目標函數隨定平臺球鉸短邊對應的圓心角變化曲線
從圖6可以看出:目標函數f1(x)的值與定平臺球鉸短邊對應的圓心角成正相關的關系,目標函數f2(x)的值與定平臺球鉸短邊對應的圓心角成正相關的關系。
2.5 初始高度對目標函數的影響
在ADAMS中研究初始高度對目標函數的影響。目標函數隨初始高度變化曲線如圖7所示。
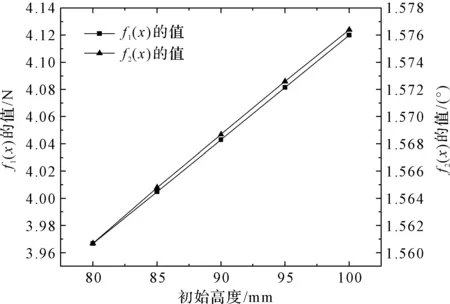
圖7 目標函數隨初始高度變化曲線
從圖7可以看出:目標函數f1(x)的值與初始高度成正相關的關系,目標函數f2(x)的值與初始高度成正相關的關系。
3 并聯機構的優化
本文第2節研究了設計變量的變化對目標函數f1(x)和目標函數f2(x)的影響,發現同一個設計變量的變化,往往會使不同的目標函數產生不同的(甚至是截然相反的)變化趨勢。因此,為了使并聯機構的性能最優,需要對其進行多目標優化設計。
3.1 基于線性加權和法的多目標優化
本文采用線性加權和法將多目標優化問題重新構造成一個新的評價函數,從而將多目標優化問題轉變為求評價函數的單目標優化問題[15],即:
(9)
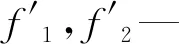
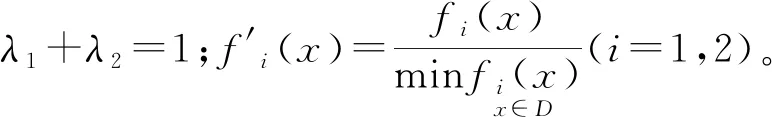
在ADAMS中進行單目標的優化可得:
因為目標函數f1(x)優化的目標是盡可能地小,目標函數f2(x)優化的目標是盡可能地大,它們的優化方向相反,故對f2(x)取負值進行計算;取λ1=0.8,λ2=0.2。
綜上所述,其評價函數為:
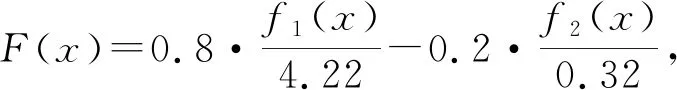
(10)
在ADAMS中進行多目標的優化,其優化過程的設置如圖8所示。
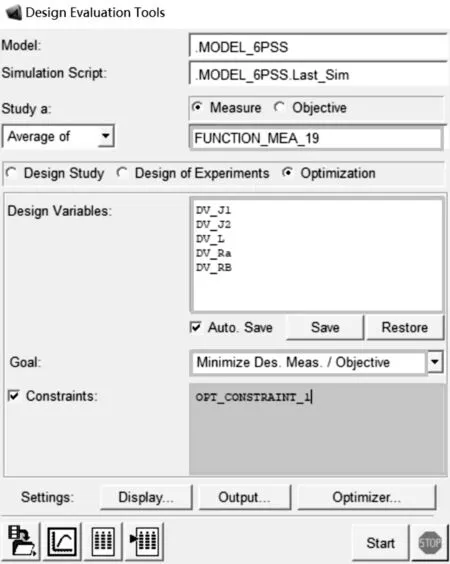
圖8 并聯機構的多目標優化
圖8中,min(FUNCTION_MEA_19)=minF(x),DV_J1=α,DV_J2=β,DV_L=H,DV_Ra=r,DV_RB=R,OPT_CONSTRAINT_1=MEA_ANGLE_i-30°≤0。
然后,利用ADAMS集成的優化算法進行優化,優化后的結構變量如表3所示。
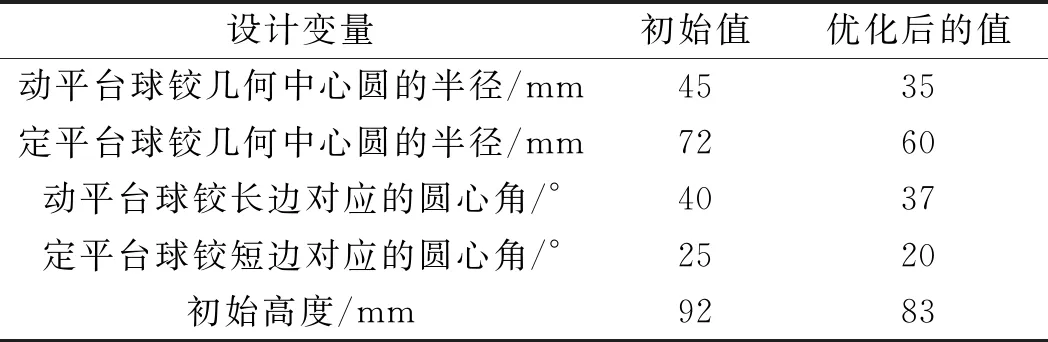
表3 并聯機構優化前后的參數值
在ADAMS中,筆者對6PSS并聯機構優化前后的移動副驅動力的最大值和動平臺的質心轉角最小值進行測量。
移動副驅動力最大值變化曲線結果如圖9所示。
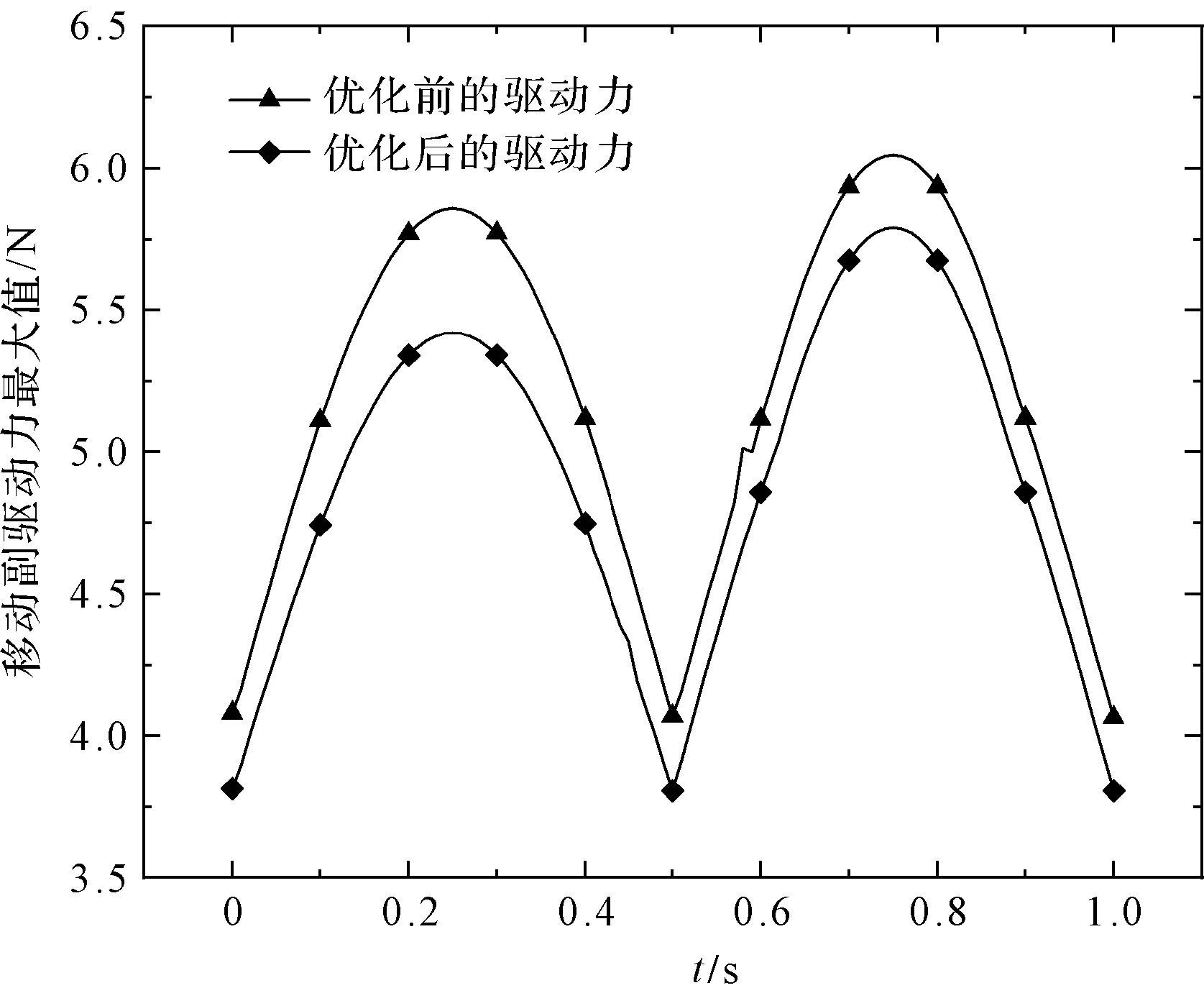
圖9 優化前后移動副驅動力最大值變化曲線
動平臺質心轉角最小值變化曲線如圖10所示。
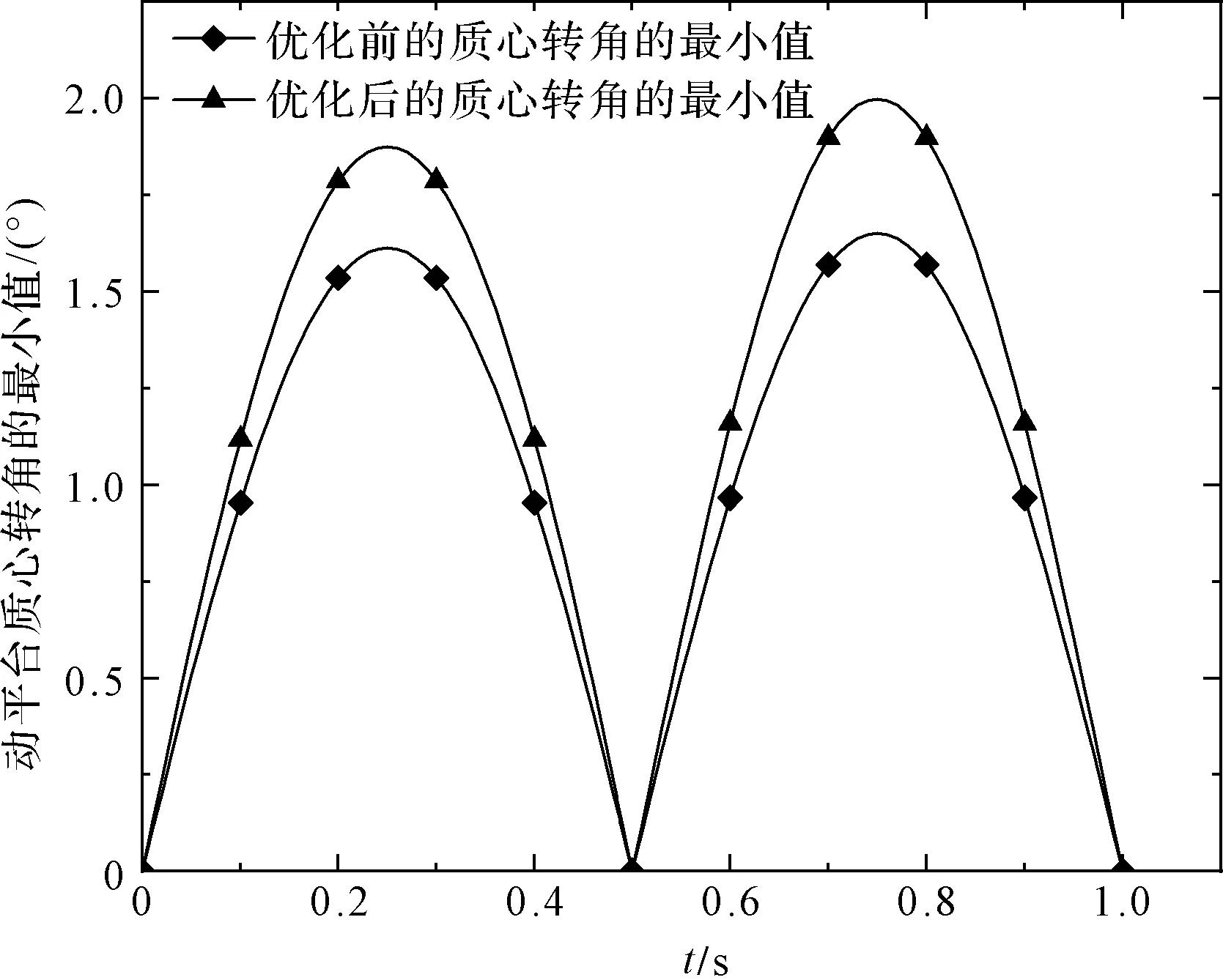
圖10 優化前后動平臺質心轉角最小值變化曲線
由圖(9,10)可知:優化后,移動副驅動力最大值的均值比初始值減小了6.5%,動平臺質心轉角最小值的均值比初始值增大了17.9%。
同時,筆者在并聯機構的運動空間內選取了7組典型的靜態的不同的位姿,測量6個移動副在優化前后最大的驅動力,如圖11所示。
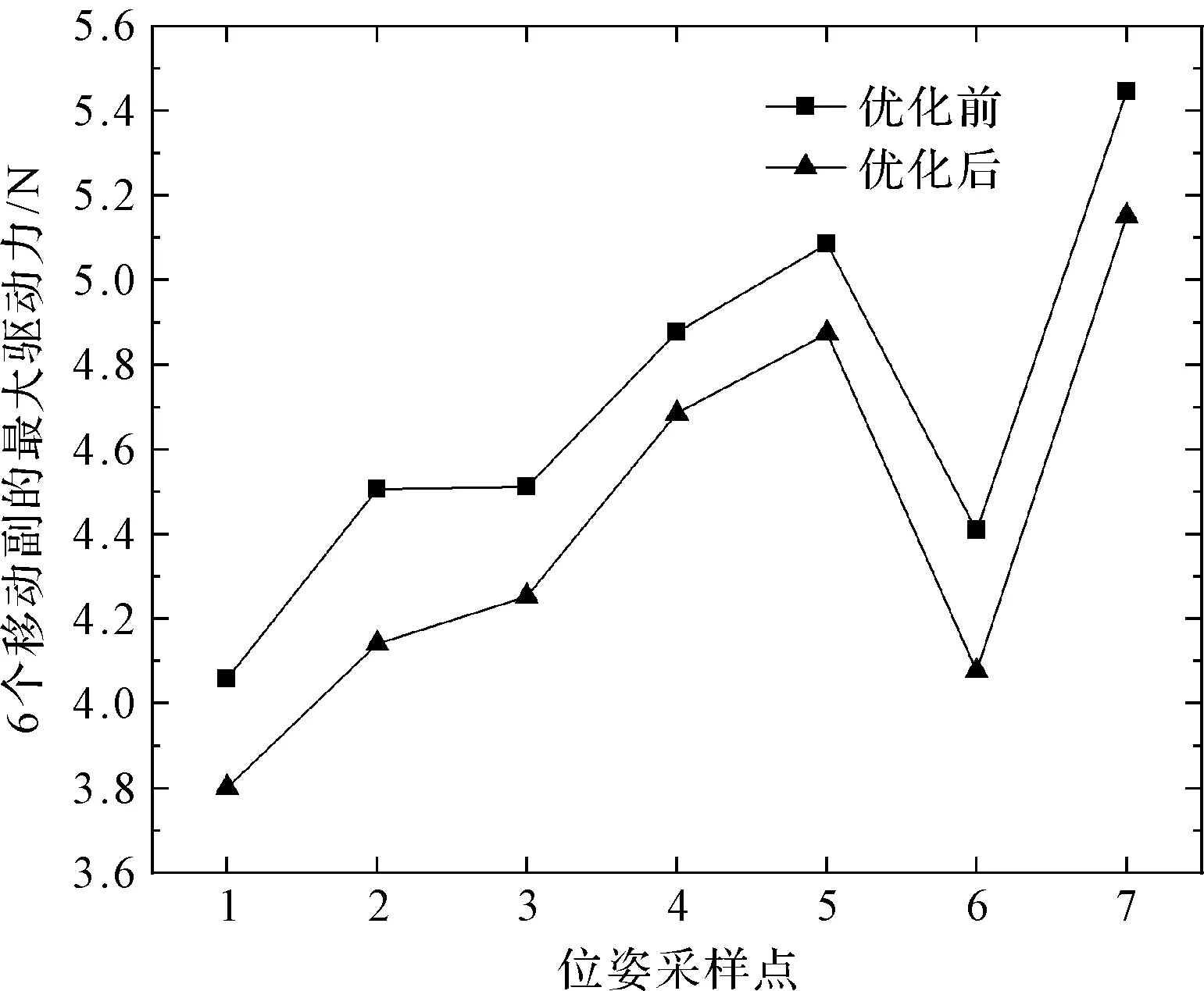
圖11 靜平衡下不同位姿6個移動副最大驅動力優化前后變化曲線
由圖11可知:優化后在靜態位姿下,移動副的最大驅動力減小了,從而提高了電機的重力補償能力。
3.2 基于蒙特卡羅法的工作空間分析
蒙特卡羅法是一種通過隨機抽樣來解決數學問題的數值方法,該方法特別適用于計算由復雜曲面包圍的體積[16,17]。例如機械手工作空間的體積,因為它在計算工作空間體積時不需要邊界曲面的分析表達式;相反,只需要確定機械手末端的參考點是否可以到達空間中隨機選擇的點。6PSS并聯機構的工作空間是一個不規則的三維曲面所包圍的區域,因此,本文采用蒙特卡羅法對6PSS并聯機構的工作空間進行求解。
該方法是基于并聯機構的運動學位置逆解而進行的一種搜索方法。其原理如下:首先給出一個包含并聯機構工作空間的范圍,在此范圍內,產生大量隨機的點;然后由機構的運動學逆解判斷每一點是否滿足約束條件,如果滿足約束條件則是空間內的點,如果不滿足,則剔除[18,19]。所有滿足約束條件的點組成了機構的工作空間。
由蒙特卡羅法得出的值并不是一個精確值,而是一個近似值,但是當投點的數量越來越大時,這個近似值也越接近真實值。文獻[20]中首次基于蒙特卡羅法給出了計算機械手工作空間的公式,即公式(11);并給出了幾個實際的例子,從而證明了蒙特卡羅法是一種簡單、易于實現、自然適用于計算機應用的方法,即:
式中:V1—機構的工作空間體積;V2—總的給定空間體積;n—機構滿足約束條件的位置點數;N—總的點數。
根據蒙特卡羅法求解工作空間的原理,筆者在MATLAB中進行編程和仿真,求得優化前后的n/N的數值,如表4所示(N=1000 000)。

表4 優化前后n/N的數值對比
優化前的工作空間為:40×40×20×0.081=2 592 mm3,優化后的工作空間為40×40×20×0.089=2 848 mm3;可見,其工作空間提高了9.8%。
優化前的工作空間如圖12所示。
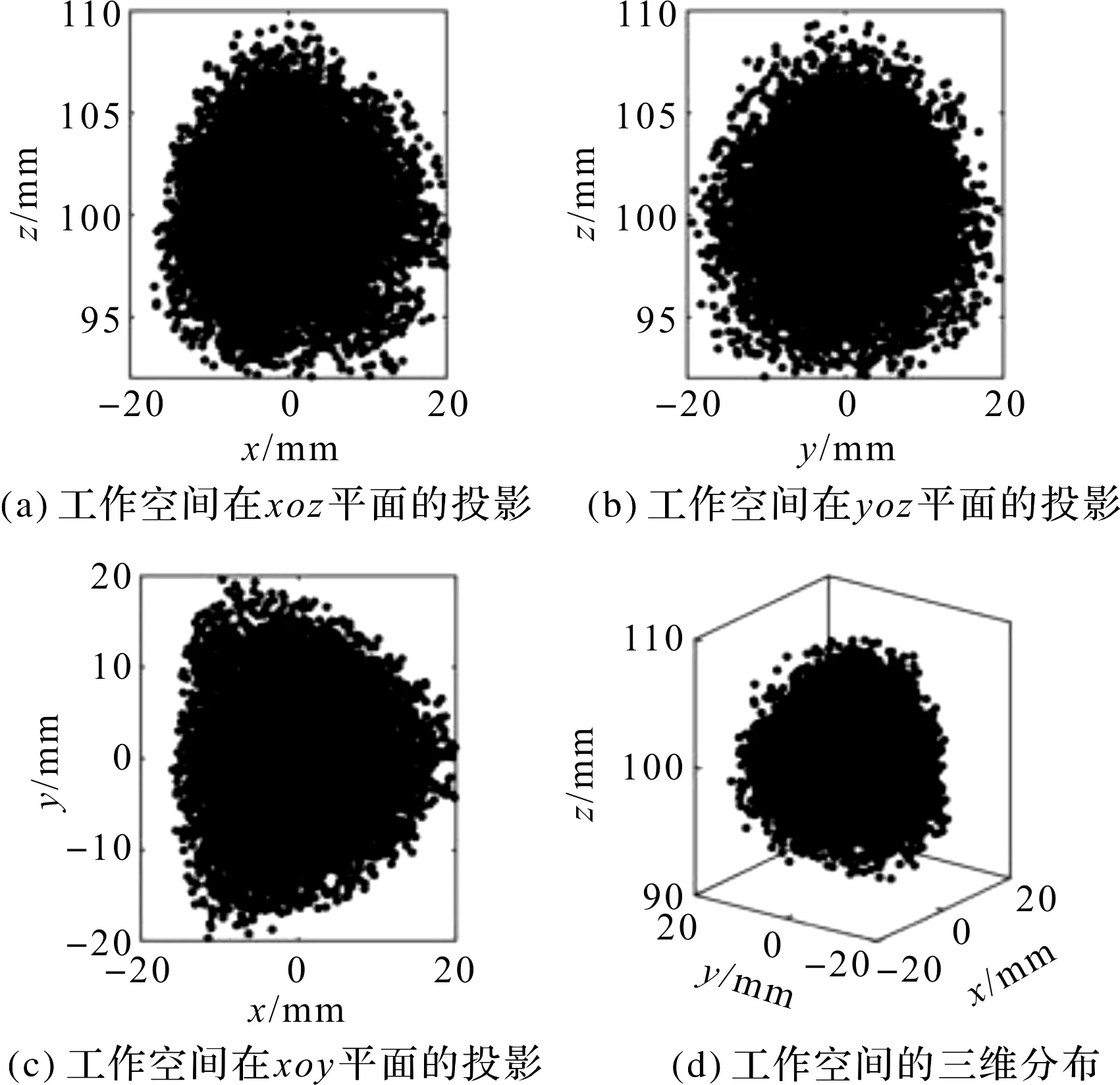
圖12 優化前機構的工作空間
優化后的工作空間如圖13所示。
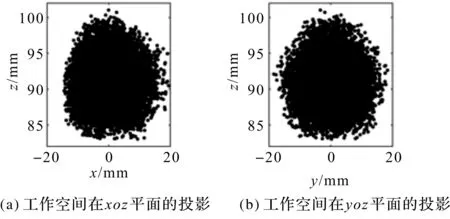
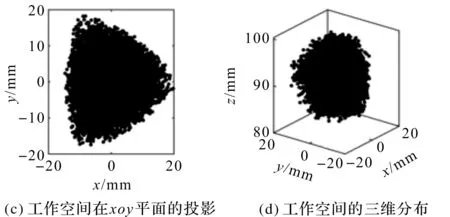
圖13 優化后機構的工作空間
4 結束語
本文基于ADAMS軟件對6PSS并聯機構進行了多目標的優化設計;首先建立了機構的參數化模型、約束條件和目標函數,然后研究了設計變量的變化對單目標函數的影響,最后采用線性加權和法,進行了多目標優化,優化后移動副驅動力最大值的均值比初始值減小了6.5%;利用蒙特卡羅法計算了機構的工作空間,優化后工作空間提高了9.8%,提高了機構的承載能力,擴大了機構的運動范圍。
與其他多目標優化方法相比,這種方法更為簡單、直觀,可以高效率地用于多參數的復雜并聯機構的優化設計。

