基于改進(jìn)的度折扣方法研究社交網(wǎng)絡(luò)影響力最大化問題

夏 欣，馬 闖，張海峰*

(1.安徽大學(xué)數(shù)學(xué)科學(xué)學(xué)院 合肥230601；2.安徽大學(xué)互聯(lián)網(wǎng)學(xué)院 合肥 230601)

在線社交平臺(tái)如Twitter、Weibo、WeChat、Facebook等已經(jīng)成為人們生活中不可或缺的重要工具，引起了不同領(lǐng)域的學(xué)者對(duì)社交網(wǎng)絡(luò)的廣泛關(guān)注與研究，如社交網(wǎng)絡(luò)上的影響力最大化問題、鏈路預(yù)測(cè)、社團(tuán)發(fā)現(xiàn)及推薦系統(tǒng)等[1-4]。其中影響力最大化問題因其普遍的應(yīng)用場(chǎng)景而被廣泛研究，如在廣告投放和市場(chǎng)營(yíng)銷中如何用有限的成本選擇具有較大傳播力度的人物、地點(diǎn)投放廣告，使得了解并且購(gòu)買該產(chǎn)品的用戶最多，從而獲取最大收益。在疾病和謠言的傳播鏈中，控制網(wǎng)絡(luò)中影響力大的節(jié)點(diǎn)可以避免其大規(guī)模快速傳播[5-6]。

影響力最大化問題是指在一個(gè)網(wǎng)絡(luò)中選擇一定數(shù)目的節(jié)點(diǎn)作為種子集，通過激活這些種子節(jié)點(diǎn)，使得信息在網(wǎng)絡(luò)中傳播，最終希望網(wǎng)絡(luò)中被激活的節(jié)點(diǎn)數(shù)最多。影響力最大化算法主要分為3類：貪婪算法、中心性指標(biāo)和啟發(fā)式算法。

在貪婪算法中，文獻(xiàn)[7]將影響力最大化問題定義為一個(gè)離散的優(yōu)化問題，證明了在獨(dú)立級(jí)聯(lián)模型和線性閾值模型下該問題是一個(gè)NP-Hard問題。并進(jìn)一步提出了近似比為(1?1/e)的爬山貪心算法，在每一步迭代中都選擇當(dāng)前邊際傳播范圍最廣的節(jié)點(diǎn)加入種子集。文獻(xiàn)[8]利用子模性提出了CELF(cost-effective lazy forward)算法，該算法大大減少了計(jì)算時(shí)間。文獻(xiàn)[9]提出了改進(jìn)的CELF++算法，減少了不必要的計(jì)算次數(shù)。文獻(xiàn)[10]提出NewGreedy算法，以傳播概率保留網(wǎng)絡(luò)中的邊，根據(jù)子圖的連通性考慮節(jié)點(diǎn)加入種子集的增益。由于NewGreedy算法無法保證子模性，文獻(xiàn)[11]提出了一個(gè)靜態(tài)的貪婪算法StaticGreedy算法，能夠解決影響力最大化中的精確度可擴(kuò)展性問題。貪婪算法雖然能找到影響力較大的種子節(jié)點(diǎn)，但其時(shí)間復(fù)雜度太高，不適用于大型網(wǎng)絡(luò)。

第二類解決影響力最大化問題的方法是基于網(wǎng)絡(luò)的拓?fù)浣Y(jié)構(gòu)對(duì)節(jié)點(diǎn)的影響力排序，使用中心性指標(biāo)對(duì)網(wǎng)絡(luò)中的節(jié)點(diǎn)排序，選擇前K個(gè)中心性指標(biāo)最大的節(jié)點(diǎn)作為種子節(jié)點(diǎn)[12]。基于網(wǎng)絡(luò)結(jié)構(gòu)定義的中心性指標(biāo)有度中心性指標(biāo)、接近度中心性及介數(shù)中心性等[13-16]。文獻(xiàn)[17]系統(tǒng)回顧了關(guān)鍵點(diǎn)識(shí)別中的概念和度量，并對(duì)問題和方法進(jìn)行了分類，通過廣泛的實(shí)證分析，比較不同方法的適用性。此外，很多學(xué)者提出新的影響力排序方法，如文獻(xiàn)[18]認(rèn)為種子節(jié)點(diǎn)應(yīng)該分散在網(wǎng)絡(luò)中，定義了GCC (generalized closeness centrality)指標(biāo)。文獻(xiàn)[19]提出網(wǎng)絡(luò)節(jié)點(diǎn)的H指數(shù)衡量節(jié)點(diǎn)的重要性。文獻(xiàn)[20]通過構(gòu)造算子說明了節(jié)點(diǎn)的度、H指數(shù)和核數(shù)之間的關(guān)系，該關(guān)系被定義為DHC定理。文獻(xiàn)[21]結(jié)合節(jié)點(diǎn)的K-shell值和節(jié)點(diǎn)間最短路徑長(zhǎng)度，將K-shell值看做節(jié)點(diǎn)重力，提出重力中心性指標(biāo)。

使用中心性指標(biāo)選取種子節(jié)點(diǎn)，忽略了節(jié)點(diǎn)間的重疊性，可能造成傳播過程中的冗余，為了尋找更加高效的解決方法，啟發(fā)式算法被相繼提出。如文獻(xiàn)[22]考慮局部影響區(qū)域迭代節(jié)點(diǎn)的全局影響力提出了IRIE (influence ranking influence estimation)算法。文獻(xiàn)[23]通過節(jié)點(diǎn)間的簡(jiǎn)單路徑近似計(jì)算節(jié)點(diǎn)的傳播影響力，并且考慮不同的優(yōu)化方法減少擴(kuò)展中迭代調(diào)用的次數(shù)，提出了Simpath算法。文獻(xiàn)[24]介紹了識(shí)別網(wǎng)絡(luò)中單個(gè)有影響力節(jié)點(diǎn)的方法、特點(diǎn)和性能，同時(shí)介紹利用啟發(fā)式算法尋找多個(gè)影響力節(jié)點(diǎn)的研究方法。文獻(xiàn)[25]考慮種子集到其他節(jié)點(diǎn)的最短路徑得到種子集影響范圍，提出SPM(shortest-path model)算法。文獻(xiàn)[26]基于節(jié)點(diǎn)相似性提出了啟發(fā)式的聚類算法，選取聚類質(zhì)心作為種子節(jié)點(diǎn)獲得較大傳播范圍。文獻(xiàn)[10]基于節(jié)點(diǎn)的度提出了啟發(fā)式的度折扣(degree discount,DD)算法，度折扣算法比貪婪算法的運(yùn)行速度快了近千倍，并且能達(dá)到與貪婪算法較為接近的效果，因此受到廣泛關(guān)注。

雖然度折扣算法具有快速、高效的特性，但該算法還有許多需要改進(jìn)的地方，這些不足之處是制約該算法性能進(jìn)一步提升的關(guān)鍵因素。首先，度折扣算法在計(jì)算節(jié)點(diǎn)的期望影響力時(shí)沒有考慮鄰居的差異性，而是簡(jiǎn)單地認(rèn)為每個(gè)未激活的鄰居節(jié)點(diǎn)對(duì)該節(jié)點(diǎn)期望影響力的貢獻(xiàn)是相同的，導(dǎo)致計(jì)算期望影響力的公式不夠精確。其次，度折扣算法沒有考慮節(jié)點(diǎn)之間共同鄰居數(shù)的影響，不能充分降低傳播的冗余性，比如節(jié)點(diǎn)i和j之間有許多共同鄰居，如果節(jié)點(diǎn)j已被選擇為種子節(jié)點(diǎn)，則節(jié)點(diǎn)i被感染的可能性也很高，因?yàn)樗麄冎g有多條可能的傳播路徑，此時(shí)再選擇節(jié)點(diǎn)i作為種子節(jié)點(diǎn)會(huì)導(dǎo)致傳播的冗余效應(yīng)[27]。針對(duì)以上兩個(gè)問題，本文首先對(duì)度折扣算法中計(jì)算期望影響力的公式進(jìn)行修正，然后基于共同鄰居數(shù)引入冗余弱化效應(yīng)進(jìn)一步改進(jìn)度折扣算法。

1 影響力最大化與傳播模型

1.1 影響力最大化問題描述

用網(wǎng)絡(luò)圖G=(V,E)表 示社交網(wǎng)絡(luò)，其中V是節(jié)點(diǎn)集，代表社交網(wǎng)絡(luò)中的用戶；E是邊集，代表社交網(wǎng)絡(luò)中用戶之間的關(guān)系。影響力最大化問題就是在網(wǎng)絡(luò)中找出K個(gè)節(jié)點(diǎn)作為種子集S，然后按照規(guī)定的傳播模型將信息傳播給鄰居節(jié)點(diǎn)，使得最終能影響的節(jié)點(diǎn)數(shù)最多。在特定的傳播模型M下，任意種子節(jié)點(diǎn)集S的影響力可以表示為σM(S)。因此，網(wǎng)絡(luò)上影響力最大化問題的形式化定義為：

1.2 獨(dú)立級(jí)聯(lián)模型

在獨(dú)立級(jí)聯(lián)模型(independent cascading model,IC)中，網(wǎng)絡(luò)中的節(jié)點(diǎn)有兩種可能的狀態(tài)：未激活態(tài)和激活態(tài)。同時(shí)為網(wǎng)絡(luò)中的每條邊(i,j)分配一個(gè)[0,1]間的概率值βij作為信息在該條邊上的傳播概率。IC模型具體傳播過程如下：

1)在t=0時(shí)刻，選定K個(gè)節(jié)點(diǎn)構(gòu)成種子集S0，僅將種子集中節(jié)點(diǎn)設(shè)為激活狀態(tài)，其余節(jié)點(diǎn)為未激活狀態(tài)。

2)在t+1時(shí) 刻，每一個(gè)激活節(jié)點(diǎn)i∈St，以概率βij嘗試激活鄰居中的未激活節(jié)點(diǎn)j。若激活成功，則該鄰居節(jié)點(diǎn)j由未激活狀態(tài)轉(zhuǎn)為激活狀態(tài)，否則仍保持未激活狀態(tài)。并且每個(gè)激活節(jié)點(diǎn)只有一次激活鄰居的機(jī)會(huì)，無論是否成功激活，該節(jié)點(diǎn)在下一輪將不具有激活能力。節(jié)點(diǎn)j有多個(gè)種子鄰居時(shí)，每個(gè)種子鄰居都獨(dú)立的激活節(jié)點(diǎn)j，如種子節(jié)點(diǎn)i和h均 為節(jié)點(diǎn)j的鄰居，則j被激活的概率為1?(1?βij)(1?βhj)。

3)直到某個(gè)時(shí)刻，網(wǎng)絡(luò)中所有節(jié)點(diǎn)都不再具有激活其他節(jié)點(diǎn)能力時(shí)，傳播過程結(jié)束。

2 改進(jìn)的度折扣算法

2.1 度折扣算法

度折扣算法的基本思想是：假設(shè)節(jié)點(diǎn)j是節(jié)點(diǎn)i的鄰居，如果j已被選為種子節(jié)點(diǎn)，那么在基于度中心性指標(biāo)考慮節(jié)點(diǎn)i是否作為種子節(jié)點(diǎn)時(shí)，應(yīng)該對(duì)連邊(i,j)打 折扣，因?yàn)閕對(duì)j不能產(chǎn)生額外的影響。假設(shè)所有邊的激活概率都相同，均為β。當(dāng)節(jié)點(diǎn)i的鄰居中有si個(gè)激活種子時(shí)，i被激活的概率為1?(1?β)si， 此時(shí)i節(jié)點(diǎn)能被鄰居節(jié)點(diǎn)激活，其期望影響力與直接將i節(jié)點(diǎn)選為種子節(jié)點(diǎn)的期望影響力相同，即此時(shí)選擇節(jié)點(diǎn)i作為種子節(jié)點(diǎn)不增加額外的影響力(對(duì)期望影響力的貢獻(xiàn)為0)。由于節(jié)點(diǎn)i沒有被激活的概率為(1?β)si，當(dāng)節(jié)點(diǎn)i被選為種子時(shí)，其能激活的節(jié)點(diǎn)數(shù)為1+(di?si)β，其中“1”表示節(jié)點(diǎn)i被激活，“(di?si)β”表示被激活的鄰居數(shù)。因此考慮節(jié)點(diǎn)i選為種子時(shí)，其產(chǎn)生的期望影響力為：

當(dāng)節(jié)點(diǎn)i鄰居中沒有種子節(jié)點(diǎn)時(shí)，i作為種子節(jié)點(diǎn)產(chǎn)生的期望影響力為：1 +diβ?B。設(shè) γ是對(duì)鄰居中每個(gè)種子節(jié)點(diǎn)的度折扣，則siβγ?B?A，可以得到γ=2+(di?si)β，因此，當(dāng)節(jié)點(diǎn)i有si個(gè)種子鄰居時(shí)，它的度折扣值定義為：

度折扣算法的基本步驟為：第一輪中沒有種子節(jié)點(diǎn)，所有節(jié)點(diǎn)的度都沒有被折扣，所以直接選擇網(wǎng)絡(luò)中度最大的節(jié)點(diǎn)作為第一個(gè)種子；接下來每一輪根據(jù)式(3)計(jì)算每個(gè)未被激活節(jié)點(diǎn)的度折扣值ddi，并選擇最大的一個(gè)節(jié)點(diǎn)加入種子集；循環(huán)更新計(jì)算直到選出K個(gè)種子節(jié)點(diǎn)加入種子集S。

2.2 一階改進(jìn)的度折扣算法

度折扣算法認(rèn)為所有非激活的鄰居對(duì)節(jié)點(diǎn)i貢獻(xiàn)的期望影響力都是相同的，即為β。實(shí)際上這些未激活鄰居對(duì)節(jié)點(diǎn)i貢獻(xiàn)的期望影響力是不同的，如節(jié)點(diǎn)i有兩個(gè)未激活鄰居j和l， 如果節(jié)點(diǎn)j的鄰居中已經(jīng)有很多種子，而節(jié)點(diǎn)l的鄰居中沒有種子節(jié)點(diǎn)，如果節(jié)點(diǎn)j和l均 被激活，則節(jié)點(diǎn)l有更大的可能性是被i激活的，而節(jié)點(diǎn)j很可能被其他節(jié)點(diǎn)激活。因此節(jié)點(diǎn)j和l對(duì) 節(jié)點(diǎn)i期望影響力的貢獻(xiàn)是截然不同的，如圖1a所示，其中實(shí)心黑色節(jié)點(diǎn)處于激活狀態(tài)，空心節(jié)點(diǎn)為未激活狀態(tài)。基于此，本文對(duì)計(jì)算期望影響力的公式進(jìn)行如下修正(IDD1算法)：

式中，aij表示鄰接關(guān)系，aij=0表示節(jié)點(diǎn)i與j沒有連邊，aij=1表 示節(jié)點(diǎn)i與j有連邊。在考慮節(jié)點(diǎn)i的期望影響力時(shí)需要考慮非激活鄰居節(jié)點(diǎn)自身鄰居中種子節(jié)點(diǎn)的數(shù)量，若這些非激活鄰居周圍種子節(jié)點(diǎn)越多，則對(duì)i貢獻(xiàn)的期望影響力越小。

IDD1算法的基本步驟為：第一輪中直接選擇網(wǎng)絡(luò)中度最大的節(jié)點(diǎn)作為第一個(gè)種子；接下來每一輪根據(jù)式(4)計(jì)算每個(gè)非激活節(jié)點(diǎn)的期望影響力Iei，選擇最大的一個(gè)節(jié)點(diǎn)加入到種子集；循環(huán)更新計(jì)算直到選出K個(gè)種子加入S。

2.3 二階改進(jìn)的度折扣算法

在選擇多個(gè)節(jié)點(diǎn)作為種子節(jié)點(diǎn)時(shí)，除了要考慮節(jié)點(diǎn)自身的重要性，另一個(gè)重要因素是如何確保種子節(jié)點(diǎn)在網(wǎng)絡(luò)上分布充分分散，避免傳播的冗余性。考慮如下情景：節(jié)點(diǎn)i與節(jié)點(diǎn)j之間有許多共同鄰居，對(duì)于IC模型而言，若節(jié)點(diǎn)j已經(jīng)被選擇為種子節(jié)點(diǎn)，則節(jié)點(diǎn)i有很大的概率被激活(通過直接連邊激活和多個(gè)共同鄰居激活)，此時(shí)再選擇節(jié)點(diǎn)i作為種子節(jié)點(diǎn)對(duì)提高傳播影響力的作用是非常有限的，因此選擇的種子節(jié)點(diǎn)之間應(yīng)該避免有多個(gè)共同鄰居的情況，如圖1b所示。基于此，本文在IDD1算法基礎(chǔ)上引入基于共同鄰居數(shù)的冗余弱化機(jī)制，保證種子節(jié)點(diǎn)的分布足夠分散。令Cij為節(jié)點(diǎn)i和j的共同鄰居數(shù)，定義節(jié)點(diǎn)i的影響期望力為Cei，則：

圖1 網(wǎng)絡(luò)示例圖

式中， α>0是可調(diào)參數(shù)，如果 α太大會(huì)導(dǎo)致所有鄰居的貢獻(xiàn)為0，若 α太小會(huì)導(dǎo)致鄰居的貢獻(xiàn)差異性被忽略，本文取α =0.05。

IDD2算法的基本步驟如下：首先選擇網(wǎng)絡(luò)中度最大的節(jié)點(diǎn)作為第一個(gè)種子；之后每一輪根據(jù)式(5)計(jì)算其他未激活節(jié)點(diǎn)的Cei，選擇 Cei值最大的節(jié)點(diǎn)作為種子；循環(huán)更新計(jì)算直到選出K個(gè)種子加入S。

3 實(shí)驗(yàn)與分析

本文在4個(gè)真實(shí)網(wǎng)絡(luò)上對(duì)本文提出的IDD1算法和IDD2算法進(jìn)行性能測(cè)試，使用IC模型與一些啟發(fā)式算法進(jìn)行比較，包括度折扣算法(DD)、度中心性算法(degree)以及隨機(jī)選擇種子算法(random)。本文沒有與貪婪算法進(jìn)行比較，一方面是因?yàn)樨澙匪惴ǖ臅r(shí)間復(fù)雜度太高，對(duì)于規(guī)模上萬的節(jié)點(diǎn)非常耗時(shí)。另一方面，如文獻(xiàn)[10]所述，度折扣算法雖然是一種啟發(fā)式算法，但是該算法的性能接近于貪婪算法。實(shí)驗(yàn)結(jié)果表明了本文提出的IDD1算法和IDD2算法性能均優(yōu)于度折扣算法，因此更接近于貪婪算法。另外這兩個(gè)算法均是基于局部網(wǎng)絡(luò)結(jié)構(gòu)的啟發(fā)式算法，與度折扣算法的時(shí)間復(fù)雜度接近。

3.1 數(shù)據(jù)集與實(shí)驗(yàn)設(shè)置

表1 4個(gè)經(jīng)驗(yàn)網(wǎng)絡(luò)的結(jié)構(gòu)性質(zhì)

本文使用IC模型作為傳播模型，每條邊上的激活概率均為β，從最終激活節(jié)點(diǎn)的比例、傳播速度以及運(yùn)行時(shí)間3方面比較不同算法的優(yōu)劣性。為了保證結(jié)果的可靠性，所有方法均獨(dú)立傳播1000次取平均結(jié)果。

3.2 實(shí)驗(yàn)結(jié)果

3.2.1獨(dú)立級(jí)聯(lián)模型

本文在4個(gè)真實(shí)網(wǎng)絡(luò)上比較了不同算法選擇種子集的影響范圍和傳播速度，并且定義了種子集的平均度和平均最短路徑長(zhǎng)度解釋模型的有效性。

1)影響范圍

圖2顯示了不同算法產(chǎn)生的最終傳播范圍隨著種子數(shù)K的變化情況，用 σ(S)表示激活節(jié)點(diǎn)占網(wǎng)絡(luò)的比例。前3個(gè)網(wǎng)絡(luò)的傳播率均設(shè)為0.1，由于第4個(gè)網(wǎng)絡(luò)傳播閾值較小，傳播率設(shè)置為0.06。由圖2可知：度折扣算法比度中心性算法以及隨機(jī)算法更能提高傳播范圍，而本文提出的IDD1算法雖然只是對(duì)度折扣算法的公式進(jìn)行簡(jiǎn)單修正，但實(shí)驗(yàn)結(jié)果表明該算法在4個(gè)真實(shí)網(wǎng)絡(luò)均優(yōu)于度折扣算法。當(dāng)考慮冗余弱化機(jī)制時(shí)，IDD2算法能夠更加明顯地提高擴(kuò)散范圍。對(duì)于網(wǎng)絡(luò)規(guī)模比較小的TAP網(wǎng)絡(luò)而言，在種子數(shù)較小時(shí)，IDD1算法優(yōu)勢(shì)比較明顯，而對(duì)于較大的網(wǎng)絡(luò)而言，IDD1的優(yōu)勢(shì)在種子數(shù)較多時(shí)能更加凸顯。

圖2 最終影響范圍隨著種子數(shù)的變化情況

圖3是在固定種子數(shù)的情況下進(jìn)一步研究最終傳播范圍隨著不同傳播概率β的變化情況，其中TAP網(wǎng)絡(luò)20個(gè)種子，Ca-GrQc和PGP網(wǎng)絡(luò)50個(gè)種子，Ca-CondMat網(wǎng)絡(luò)70個(gè)種子。實(shí)驗(yàn)結(jié)果再次表明，IDD1算法比度折扣算法更能提高擴(kuò)散范圍，而引入冗余弱化機(jī)制的IDD2算法則在所有網(wǎng)絡(luò)上都是效果最顯著的。

圖3 最終影響范圍隨著傳播率的變化情況

2)傳播速度

本文在固定種子數(shù)量以及傳播率β的情況下，比較不同算法對(duì)傳播速度的影響，如圖4所示。其中，TAP網(wǎng)絡(luò)固定β=0.1，K=20；Ca-GrQc網(wǎng)絡(luò)和PGP網(wǎng)絡(luò)固定β=0.1，K=50；Ca-CondMat網(wǎng)絡(luò)固定β=0.06，K=70。t表示信息傳播的迭代過程，用σt(S)記錄每次傳播后網(wǎng)絡(luò)中激活節(jié)點(diǎn)比例。從實(shí)驗(yàn)結(jié)果可以看出IDD1算法從一開始就以較快的速度擴(kuò)散信息，并且最終傳播范圍也高于已有算法。

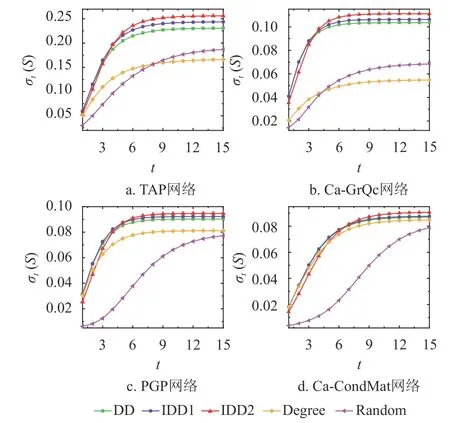
圖4 影響范圍隨著時(shí)間的變化情況

IDD2算法在前幾步傳播過程中傳播范圍略低于度折扣算法和IDD1算法，這是由于IDD2算法選擇的種子在網(wǎng)絡(luò)中較為分散，因此需要經(jīng)過一個(gè)短暫的醞釀過程。經(jīng)過一小段時(shí)間后(3～6個(gè)時(shí)間步)，IDD2算法的傳播速度快速反超其他算法，并且得到的最終傳播范圍在所有算法中最廣。從圖2～圖4可以發(fā)現(xiàn)，無論是最終傳播范圍還是傳播速度，相比于其他算法，IDD1和IDD2算法都能取得更好的性能。

3)種子集性質(zhì)

式中，Lij是 節(jié)點(diǎn)i和節(jié)點(diǎn)j的最短路徑長(zhǎng)度；〈L〉S指標(biāo)越大，種子之間越分散。

此外，種子節(jié)點(diǎn)的平均度〈d〉S隨種子數(shù)的變化情況如圖5所示，而種子節(jié)點(diǎn)間平均最短路徑〈L〉S隨種子數(shù)的變化情況如圖6所示。其中TAP網(wǎng)絡(luò)、Ca-GrQc網(wǎng)絡(luò)和PGP網(wǎng)絡(luò)的傳播率設(shè)為0.1，Ca-CondMat網(wǎng)絡(luò)的傳播率設(shè)為0.06。從圖5和圖6可以發(fā)現(xiàn)，雖然度中心性算法能保證種子節(jié)點(diǎn)的〈d〉S最大，但是基于該算法得到的〈L〉S值均小于度折扣算法以及IDD1和IDD2算法對(duì)應(yīng)的值。反之，雖然隨機(jī)算法能保證種子節(jié)點(diǎn)的〈L〉S值最大，但是 〈d〉S值最小。度中心性算法和隨機(jī)算法只能保證影響力最大化中兩個(gè)關(guān)鍵因素中的某一條：1)種子節(jié)點(diǎn)自身很重要；2)種子節(jié)點(diǎn)足夠分散地分布在網(wǎng)絡(luò)上。度折扣算法以及改進(jìn)算法得到的〈d〉S值雖然小于度中心性算法對(duì)應(yīng)的值，但是遠(yuǎn)高于隨機(jī)算法得到的值，并且〈L〉S大于度中心性算法對(duì)應(yīng)的值。因而度折扣算法及改進(jìn)算法平衡了種子節(jié)點(diǎn)自身的重要性和種子節(jié)點(diǎn)之間距離兩個(gè)因素，可以更有效地?cái)U(kuò)大傳播范圍。尤為重要的是，雖然IDD1選擇的種子節(jié)點(diǎn)的〈d〉S值以及〈L〉S值和度折扣算法對(duì)應(yīng)的值都非常接近，但是該算法的傳播范圍更廣、傳播速度更快(如圖2～圖4)。因?yàn)镮DD2算法充分考慮了冗余弱化機(jī)制，所以該算法得到的〈L〉S值比其他非隨機(jī)算法得到的值都大。當(dāng)然，基于IDD2算法選出的種子節(jié)點(diǎn)的〈d〉S值也一定程度地變小，但是遠(yuǎn)高于隨機(jī)算法得到的〈d〉S值。IDD2算法在IC模型中的最優(yōu)性能也說明，對(duì)于IC模型而言，種子節(jié)點(diǎn)間的分散程度是能否保證影響力最大化的一個(gè)尤為重要的因素。

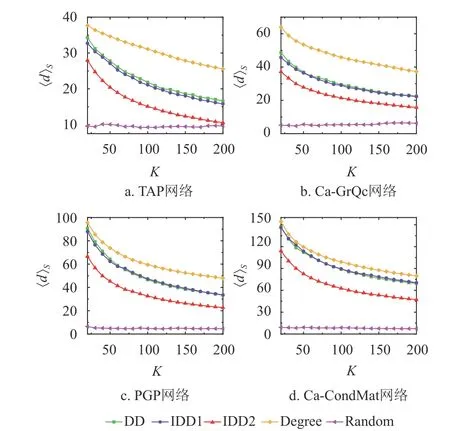
圖5 種子節(jié)點(diǎn)間平均度隨著種子數(shù)的變化情況

圖6 種子節(jié)點(diǎn)間平均最短路徑隨著種子數(shù)的變化情況

為了更為直觀地表明改進(jìn)算法選取出種子節(jié)點(diǎn)的特點(diǎn)，本文對(duì)Word網(wǎng)絡(luò)[31]進(jìn)行可視化分析，圖7中節(jié)點(diǎn)的大小與度成正相關(guān)。分別使用度中心性算法、IDD1算法和IDD2算法選取20個(gè)種子節(jié)點(diǎn)，傳播率設(shè)為0.1。種子節(jié)點(diǎn)在網(wǎng)絡(luò)中用實(shí)心黑點(diǎn)標(biāo)記，通過可視化可以直觀地看出，IDD1算法選出的種子節(jié)點(diǎn)仍包含了部分大度節(jié)點(diǎn)，IDD2算法選取的種子節(jié)點(diǎn)則更加均勻地分散在網(wǎng)絡(luò)中，種子節(jié)點(diǎn)的度也相對(duì)減小。

圖7 Word網(wǎng)絡(luò)種子節(jié)點(diǎn)可視化圖

另外也測(cè)試了這些算法在線性閾值模型(linear threshold model,LT)中的性能，IDD1算法效果仍優(yōu)于度折扣算法，然而IDD2算法在LT模型中效果一般，這是由于當(dāng)種子節(jié)點(diǎn)過于分散時(shí)，LT模型的激活條件難以滿足，故不適用于LT模型。

3.2.2未知傳播率

在度折扣算法中，作者假設(shè)節(jié)點(diǎn)真實(shí)傳播率是已知的，因而利用真實(shí)傳播率計(jì)算節(jié)點(diǎn)的期望影響力，但在實(shí)際情況下，鑒于問題的復(fù)雜性，很難知道真實(shí)傳播率的大小。為了解決此問題，一個(gè)科學(xué)、折中的方法是用傳播閾值近似代替真實(shí)傳播率，這樣做的合理性在于：傳播率太小信息不能傳播，而傳播率太大時(shí)，任何一種方法都能使得信息大范圍傳播，此時(shí)再研究哪種方法能保證影響力最大沒有太大意義。接下來的問題是：如果基于傳播閾值計(jì)算式(3)～式(5)，IDD1算法和IDD2算法是否仍然具有更優(yōu)異的表現(xiàn)。

圖8顯示了傳播閾值近似代替?zhèn)鞑ヂ蕰r(shí)最終影響范圍。將前3個(gè)網(wǎng)絡(luò)的真實(shí)傳播率設(shè)為0.1，第4個(gè)網(wǎng)絡(luò)的真實(shí)傳播率設(shè)為0.06，而期望影響力是用 βth代 替 β計(jì)算得到的，然后比較了不同算法對(duì)最終影響范圍σ(S)的影響。從圖8可以發(fā)現(xiàn)，對(duì)于IC模型而言，IDD1算法依然優(yōu)于度折扣算法，IDD2算法在檢查影響力最大化方面的性能更加突出。

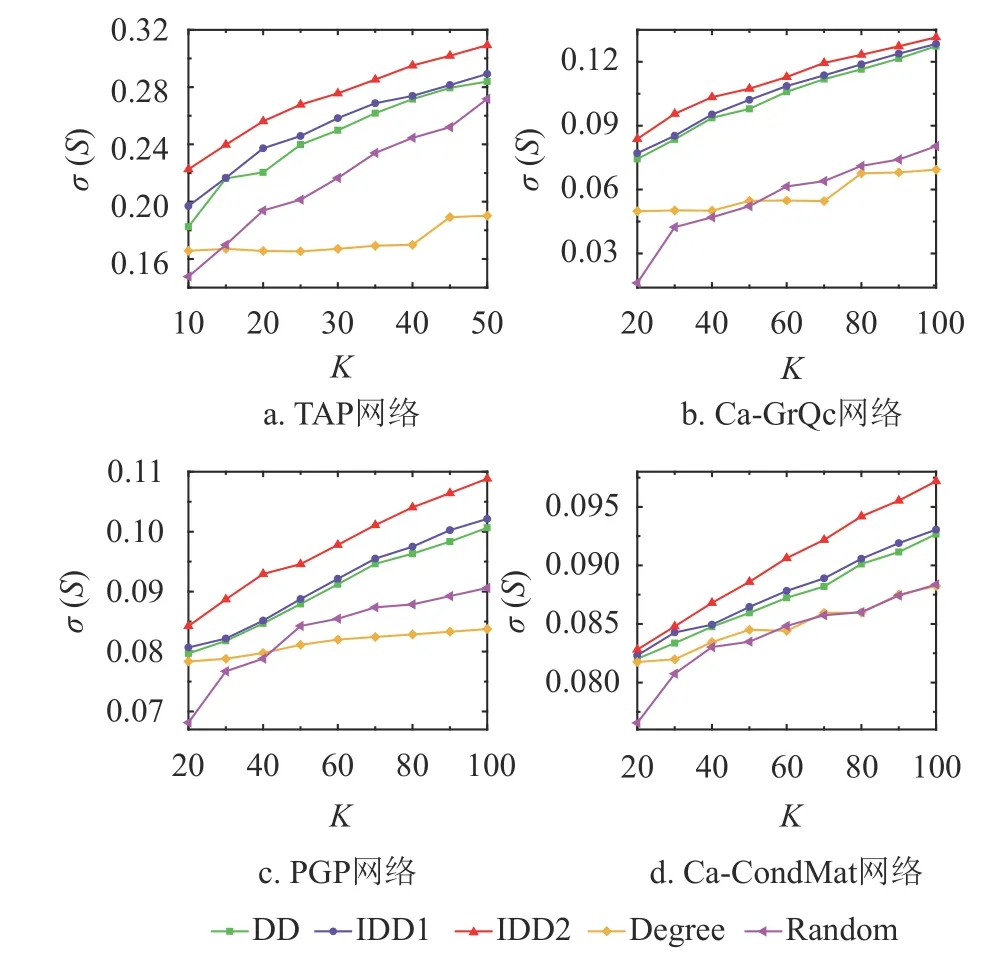
圖8 傳播閾值近似代替?zhèn)鞑ヂ蕰r(shí)最終影響范圍

3.2.3敏感性分析

考慮IDD2算法中參數(shù)α的取值情況，本文進(jìn)行了敏感性分析，其中TAP網(wǎng)絡(luò)固定 β=0.1，K=20；Ca-GrQc網(wǎng)絡(luò)和PGP網(wǎng)絡(luò)固定 β=0.1，K=50，Ca-CondMat網(wǎng)絡(luò)固定β=0.06，K=70。針對(duì)不同的網(wǎng)絡(luò)，如果網(wǎng)絡(luò)較為稠密，則節(jié)點(diǎn)共同鄰居數(shù)較多；若網(wǎng)絡(luò)較為稀疏，共同鄰居數(shù)很少。此時(shí)若α太大，指標(biāo)將趨于0，若α 太小，鄰居的貢獻(xiàn)差異性易被忽略，因此本文在[0,0.1]的范圍內(nèi)觀察IDD2算法的性能。當(dāng)α=0時(shí)，IDD2算法退化為IDD1算法，即為IDD1算法的最終影響范圍。從圖9可以看出 α取值在0.01～0.1時(shí)，IDD2算法效果均優(yōu)于IDD1算法，并且α取值為0.02～0.1時(shí)，效果相對(duì)穩(wěn)定，因此本文將實(shí)驗(yàn)參數(shù)統(tǒng)一為0.05。

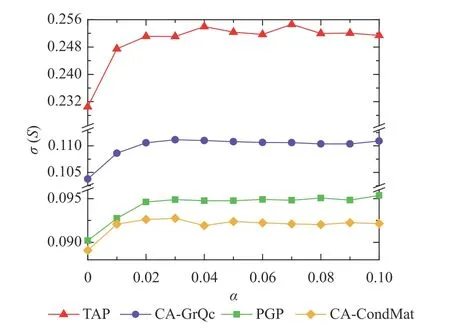
圖9 參數(shù)α 對(duì)IDD2算法的最終影響范圍的影響

3.2.4運(yùn)行時(shí)間

圖10比較了不同算法選擇50個(gè)種子的運(yùn)行時(shí)間，TAP網(wǎng)絡(luò)、Ca-GrQc網(wǎng)絡(luò)和PGP網(wǎng)絡(luò)傳播率設(shè)為0.1，Ca-CondMat網(wǎng)絡(luò)設(shè)為0.06。由圖可知，IDD1算法和IDD2算法的運(yùn)行時(shí)間略高于度折扣算法。考慮冗余弱化機(jī)制的IDD2算法運(yùn)行時(shí)間最長(zhǎng)，這是因?yàn)樵诳紤]節(jié)點(diǎn)度折扣時(shí)需要考慮每個(gè)鄰居節(jié)點(diǎn)的種子鄰居數(shù)，故復(fù)雜度要高于原度折扣算法，但度折扣算法相較于貪婪算法仍然具有高效性。

圖10 不同算法選擇種子節(jié)點(diǎn)的運(yùn)行時(shí)間

4 結(jié)束語

研究社交網(wǎng)絡(luò)影響力最大化問題具有重要的理論意義和應(yīng)用價(jià)值，在眾多檢測(cè)算法中，由于度折扣算法具有快速、高效的性能，受到學(xué)者們的廣泛關(guān)注。考慮到度折扣算法在計(jì)算節(jié)點(diǎn)期望影響力時(shí)沒有區(qū)別對(duì)待鄰居中未激活節(jié)點(diǎn)的差異性，本文對(duì)計(jì)算期望影響力的公式進(jìn)行了修正，得到了一階改進(jìn)的度折扣(IDD1)算法。為了進(jìn)一步保證選擇的種子節(jié)點(diǎn)充分分散地分布在網(wǎng)絡(luò)上，本文提出了二階改進(jìn)的度折扣(IDD2)算法。通過在4個(gè)真實(shí)網(wǎng)絡(luò)上的實(shí)驗(yàn)結(jié)果表明，IDD1算法影響的最終傳播范圍和傳播速度均優(yōu)于度折扣算法，而IDD2算法在IC模型上擴(kuò)大影響力范圍的效果尤為突出。通過計(jì)算種子節(jié)點(diǎn)之間的平均度以及平均距離，闡述了為何本文提出的算法能更有效地?cái)U(kuò)大傳播范圍。此外，考慮到真實(shí)傳播率難以獲取，本文利用傳播閾值代替真實(shí)傳播率計(jì)算期望影響力，研究結(jié)果表明本文提出的算法依然有效。