孤島模式單相光伏并網逆變器自抗擾控制策略
何國鋒
(河南城建學院 電氣與控制工程學院,河南 平頂山467036)
0 引言
由光伏、風電等分布式發電組成的微電網可以有效降低碳排放量[1]。微電網根據實際運行狀況,可分為孤島運行模式和并網運行模式。當微電網處于孤島運行模式時,逆變器處于電壓工作模式;當微電網與主電網相連,逆變器則處于并網模式,此時須要對入網電流進行控制,使入網電流達到并網標準。根據實際運行工況和發電需求,微電網能進行實時的并/離網無縫切換運行[2]。微電網處于孤島運行模式時,單相逆變器在運行的過程中會產生多種擾動,例如負載突變、非線性負載突加、濾波器元件老化導致的參數漂移等,這些不確定性因素都會對逆變器輸出的電能質量造成影響,嚴重時可能影響到微電網系統的穩定性。因此,微電網處于孤島模式時,改善控制策略使單相逆變器輸出高質量電能成為研究的重點。
為使孤島模式下微電網單相逆變器穩定、高效運行,文獻[3]考慮到負載變化的不確定性,利用逆變器的輸出信號與參考信號的偏差量設計滑模面,通過滑模自適應控制律逼近不確定性的上界,實現對負載不確定性的補償。文獻[4]將重復控制與諧振控制相結合,實現對單相逆變器性能的提高。文獻[5]針對逆變器電流內環存在擾動,提出一種平均電流前饋補償控制策略,能夠有效抑制電流內環的干擾信號。文獻[6]通過設計單相逆變器負載擾動的邊界,兼顧系統的魯棒穩定性和魯棒性能,采用改進的魯棒H∞控制方法,設計適用于單相逆變器的魯棒控制器,增強系統對不確定性擾動的抑制能力。
上述文獻沒有對單相逆變器動態抗擾性能進行詳細討論。傳統的自抗擾控制策略雖然能夠在一定程度上增強系統抗擾動性能,但是對交流信號的跟蹤速度有限,導致控制系統的動態性能不高。為了有效抑制光伏并網逆變器在孤島運行模式下的擾動、提高系統的抗擾動態性能,本文提出一種改進的單相微網逆變器自抗擾控制器設計方法。
1 微電網逆變器擾動分析
孤島模式下,微電網逆變器的主電路如圖1所示。
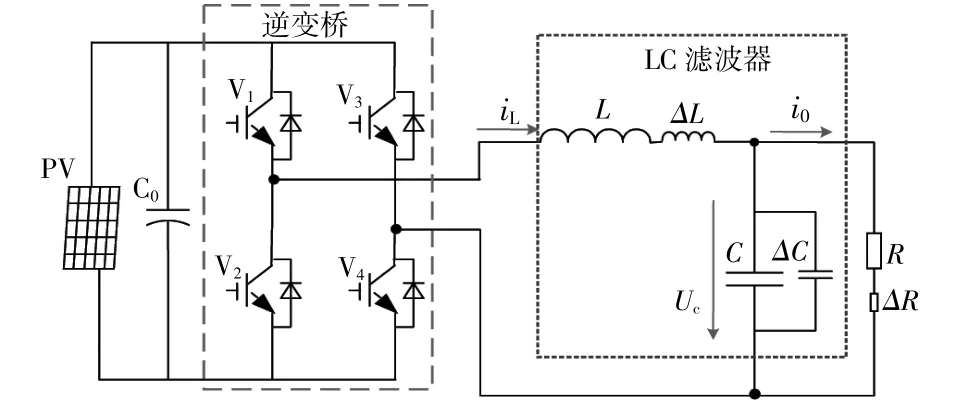
圖1 微電網逆變器主電路Fig.1 Power stage topology ofmicro-grid inverter
圖中包括光伏組件、單相全橋逆變電路、濾波電路等結構。逆變器在運行的過程中,存在著不確定性擾動,這些擾動可以分為系統外部擾動和內部參數攝動。設計控制器時考慮擾動因素,可以在一定程度上提高系統建模的精確度,提高系統的魯棒穩定性和魯棒性能[7]。
孤島模式下的微電網逆變器輸出為正弦電壓,通常采用基于內模原理的控制策略,如重復控制器、比例諧振控制器等,這類控制策略能夠實現系統的無靜差控制,但是對擾動抑制能力較差。本文通過虛擬正交方法構造出兩相交流量,再經過同步坐標變換,將其轉換成直流量,在同步旋轉坐標系下設計自抗擾控制器,控制逆變器的輸出電壓。
2 單相微電網逆變器建模
單相微電網逆變器的閉環原理圖如圖2所示,主電路結構中采用帶有LC型濾波器的單相全橋逆變器結構。圖中:L為濾波器的基準電感值;ΔL為電感值的變化量;C為基準電容值;ΔC為電容值的波動量;R為純電阻負載;ΔR為負載波動;Ui為逆變器的橋臂輸出電壓;iL為流過濾波電感的電流;i0為負載電流;UC為電容電壓,同時也是負載電壓U0。設α軸電容的電壓為UCα;電感的電流為iLα;負載的電流為i0α。

圖2 單相逆變器閉環原理圖Fig.2 Schematic diagram of single-phase inverter
將上述交流信號通過全通濾波器濾波可得β軸相應的分量:UCβ,i0β,iLα,根據基爾霍夫定律可以建立單相逆變器在αβ坐標系下的數學模型為式中:w1為α軸的擾動量;w2為β軸的擾動量;b0,b1為常數,其值大小受負載、電感值、電容值的影響[8]。
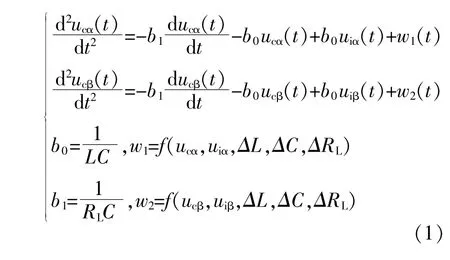
3 自抗擾控制器設計
自抗擾控制具有傳統PID控制和現代經典控制的優點。自抗擾控制器不須要準確的數學模型就能夠估算出系統的總體擾動,并對系統擾動進行實時補償。自抗擾控制器一般分為跟蹤微分器、誤差反饋控制律、擴張狀態觀測器3部分。跟蹤微分器為參考信號安排過渡過程,包括求取參考信號的微分信號;誤差反饋控制律對系統的誤差進行實時處理,產生系統的控制信號;擴張狀態觀測器需要對系統的總體擾動進行估計,估計后的擾動信號經過縮放對控制量進行補償,被補償過的信號是最終的控制信號[9]~[12]。
由式(1)和同步坐標變換可得單相微電網逆變器在同步旋轉坐標系下的數學模型為
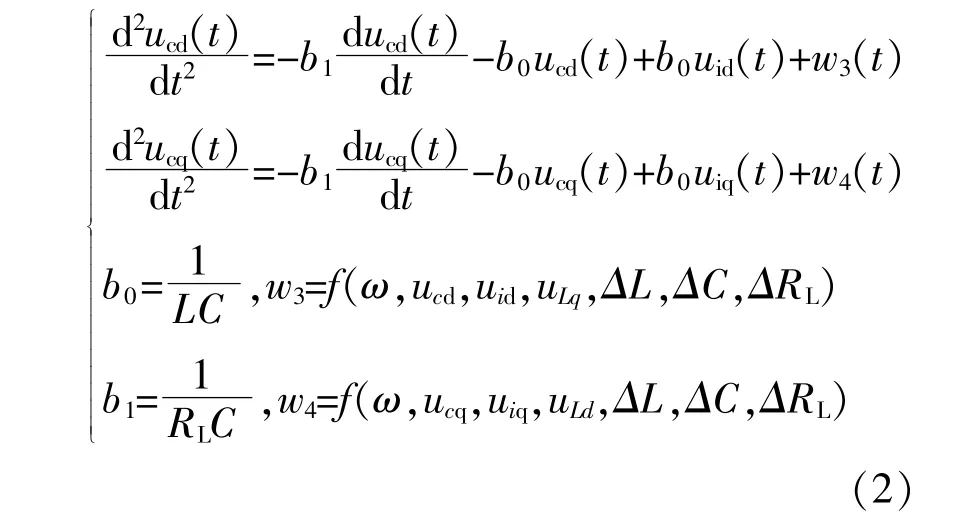
式中:w3為d軸模型受到的擾動量;w4為q軸模型受到的擾動。
同步旋轉坐標系下的單相微電網逆變器自抗擾控制器的結構如圖3所示。

圖3 d軸分量下的自抗擾控制器框圖Fig.3 Block diagram of ADRC for d-axis
圖中包括跟蹤微分器TD、非線性誤差反饋控制律NLSEF和擴張狀態觀測器ESO。擴張狀態觀測器部分的函數項f表示系統中的總擾動,包括濾波器參數的變化、負載突變、非線性負載、坐標變化時引入的耦合項等因素引起的擾動。矩陣G為誤差反饋矩陣,參與實際輸出信號與觀測信號的誤差調整。
由圖3可得二階逆變器系統模型為

二階ADRC具體算法:


非線性函數fhan與非線性函數fal的定義分別為式中:h為濾波因子,與濾波效果有關;β01,β02,β03由系統所采用的步長決定,不同的被控系統可以采取相同的β01,β02,β03。h,β01,β02,β03均為自抗擾控制器參數。
由于d軸模型與q軸模型的對稱性,本文只給出了d軸分量的自抗擾控制器的設計過程,q軸分量的自抗擾控制器設計過程及框圖不再詳細給出[13]~[15]。
基于以上的擾動分析和控制器設計結果,得到含有自抗擾控制器的單相微電網逆變器原理圖,如圖4所示。
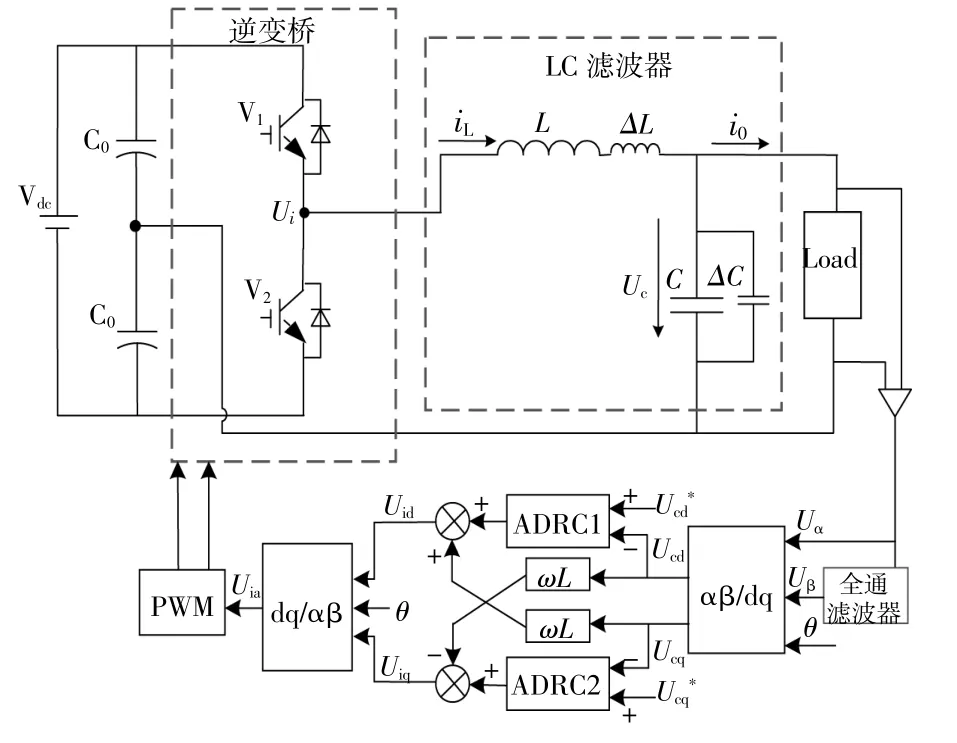
圖4 自抗擾控制下的單相微電網逆變器整體原理圖Fig.4 Overall Schematic diagram of single-phasemicro-grid inverterwith ADRC
圖中控制電路包括park變換器、自抗擾控制器、脈寬調制等部分。電壓傳感器將采集到的負載電壓信號作為靜止坐標系下的α軸分量,再將采集到的負載電壓信號進行正交旋轉,得到β軸的分量,經過park變換得到同步旋轉坐標系下的直流信號;然后,自抗擾控制器對兩相直流信號進行控制,將得到的控制信號進行坐標反變換,取α軸的控制信號作為最終的控制信號;最后,控制信號經過脈寬調制器,驅動放大作用于單相逆變器,對單相逆變器的輸出電壓進行控制。
4 仿真分析
為了進一步驗證基于虛擬矢量的自抗擾控制策略的優越性,本文利用dSPACE半實物仿真系統搭建了相應的實驗系統,并對所提控制策略進行了仿真驗證,系統相關參數如表1所示[16],[17]。

表1 單相逆變器仿真參數Table 1 System parameters of single-phase inverter
圖5為孤島模式下,單相微電網逆變器的輸出電壓和電流波形。圖6為孤島模式下單相微電網逆變器輸出電壓的THD。
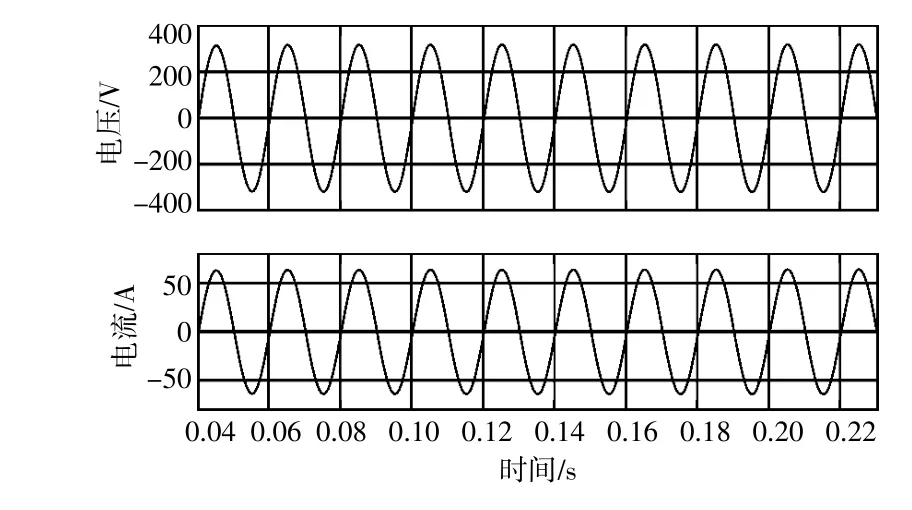
圖5 負載不變時自抗擾控制下的逆變器輸出波形Fig.5 Simulation results at constant load with ADRC

圖6負載電壓的THDFig.6 THD of output voltage at constant load with ADRC
由圖5可以看出,電壓、電流的波形是穩定光滑的正弦波。由圖6可以看出,當采用基于虛擬矢量的自抗擾控制策略時,單相微電網逆變器輸出電壓的總諧波畸變率只有0.28%,表明基于虛擬矢量的自抗擾控制策略有很好的穩態跟蹤性能。
圖7,8均為系統受到干擾時的輸出電壓和電流波形。在t=0.145 s時,對系統突加擾動,當系統受到擾動時,圖7的負載電壓沒有發生突變,而圖8中的逆變器輸出電壓產生明顯的下降。因此在系統輕載時,基于虛擬矢量的自抗擾控制策略對擾動具有更好的抑制能力。
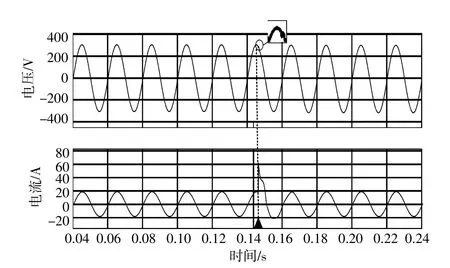
圖7 系統輕載時自抗擾控制下的逆變器輸出波形Fig.7 Simulation results at light-load with ADRC
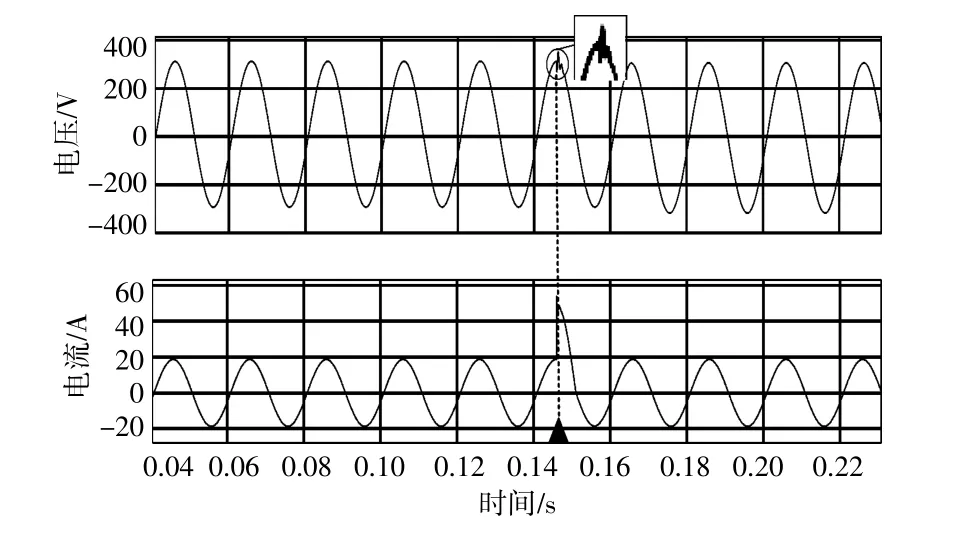
圖8 系統輕載時PI下的逆變器輸出波形Fig.8 Simulation results at light-load with PI
圖9,10均為系統重載時系統輸出的電壓和電流波形。

圖9 系統重載時自抗擾控制下的逆變器輸出波形Fig.9 Simulation results atheavy-load with ADRC
當系統突然受到擾動時,圖9逆變器輸出電壓存在波動,但是在很短的時間內,電壓即恢復正常。圖10逆變器的輸出電壓波形有明顯跌落,嚴重影響逆變器輸出的電能質量。表明基于虛擬矢量的自抗擾控制器對單相逆變器運行過程中存在的擾動有很強的抑制能力,保證了單相逆變器輸出高質量的電能。
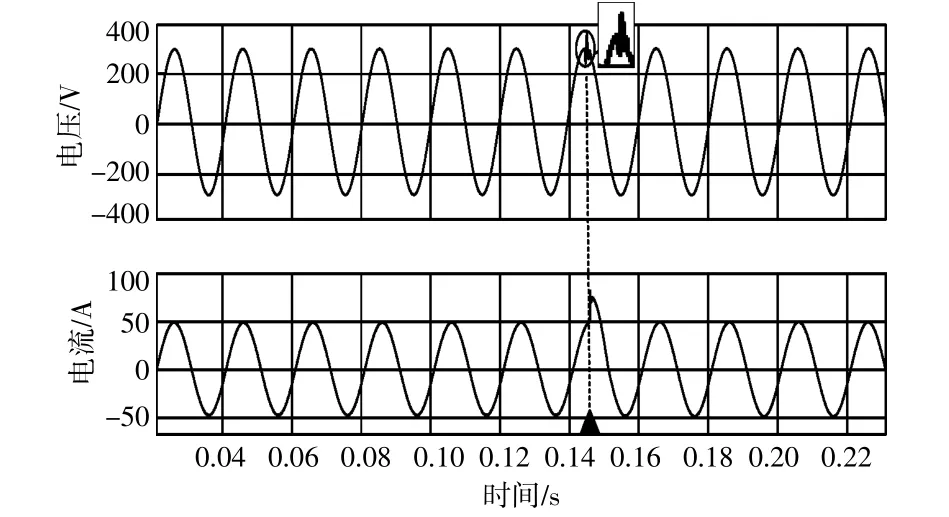
圖10 系統重載時PI下的逆變器輸出波形Fig.10 Simulation results at heavy-load with PI
負荷為非線性負載時,單相逆變器的電壓和電流波形如圖11所示。

圖11 帶非線性負載時自抗擾控制下的逆變器仿真結果Fig.11 Simulation results at non-linear load with ADRC
由圖11可知,逆變器輸出的電壓波形沒有產生畸變,電流波形光滑,與理想情況下的波形相近。仿真結果表明,基于虛擬矢量的自抗擾控制策略對非線性負載帶來的擾動具有較強的補償能力,實現逆變器高可靠性運行。
采用自抗擾控制并網逆變器的實驗結果如圖12所示。
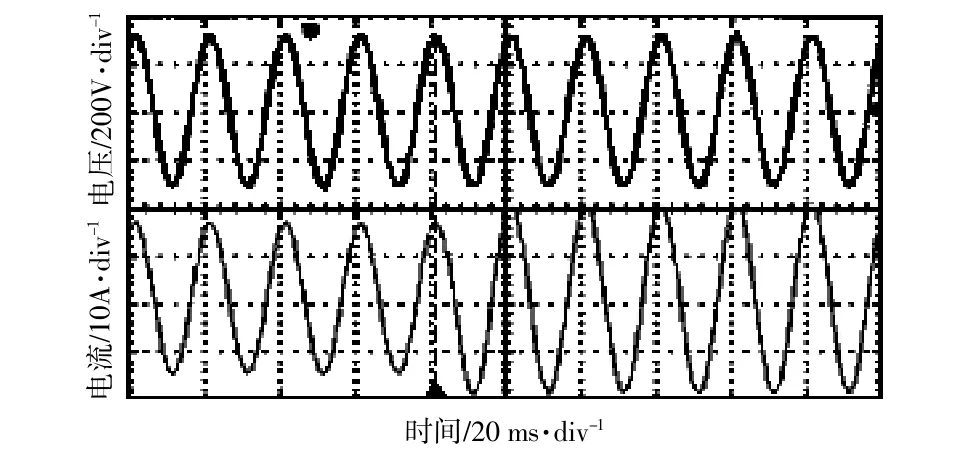
圖12 負載突變時自抗擾控制下的逆變器實驗結果Fig.12 Experimental results of inverter with ADRC under load variation
圖中:當t=80ms時,系統的負載發生突變,功率從2 kW突變到3 kW;并網逆變器的輸出電流波形幅值增加,輸出電壓波形平滑,沒有發生畸變。說明自抗擾控制策略可以有效提高系統的動態特性。
整流性負載不加擾動時,采用自抗擾控制的逆變器,在孤島模式下的穩態輸出電壓與電流實驗波形如圖13所示。

圖13 不加擾動時系統輸出的電壓和電流波形Fig.13Waveforms of output voltage and currentwithout disturbance
由圖13可以看出,孤島模式下逆變器的輸出電壓波形平滑。
采用自抗擾控制策略的逆變器電源輸出電壓和電流動態變化波形如圖14所示。

圖14 加擾動時自抗擾控制的系統輸出電壓和電流波形Fig.14Waveforms of output voltage and currentwith disturbance by ADRC
t=250ms時,系統突加負載。由圖14可以看出,當系統突加負載時,逆變器輸出電壓波形有很小的抖動,調整時間不超過5ms,表明采用本文所提的控制策略能夠較好地解決孤島模式逆變電源的擾動問題,使逆變電源在受到擾動時輸出電壓依然能夠快速恢復正常值。同時也增強了單相逆變電源系統的魯棒穩定性和魯棒性能。
5 結論
本文研究了基于虛擬矢量的自抗擾控制策略,并將其應用在孤島模式下的單相微電網逆變器中。由本文的理論研究和實驗分析可得到以下結論:①單相微電網逆變器采用基于虛擬矢量的自抗擾控制策略時,可以有效抑制系統的動態擾動。當系統重載時,自抗擾控制策略的效果更加明顯。當系統穩態運行時,逆變器輸出的電能諧波含量只有0.28%,滿足用戶的電能質量要求;②負荷為非線性負載時,單相微電網逆變器采用本文所提的控制策略可以有效抑制擾動,使系統穩定運行。

