CFRP/Al疊層材料二維正交切削過程數值仿真*

鄭華林 蒙玉培 張晟瑋

(①西南石油大學機電工程學院，四川 成都 610500；②中國航發航空科技股份有限公司，四川 成都 610500)

由碳纖維增強聚合物(CFRP)和Al合金構成的疊層材料，以其優良的綜合力學性能，廣泛應用于航空領域，其構件常以螺栓連接進行裝配，因此鉆削加工必不可少。但由于兩種材料性能的差異性，對加工帶來一定難度，容易造成各種加工缺陷[1-2]。隨著計算機技術的高速發展以及有限元理論的逐漸成熟，數值仿真成為了有力的研究方法。

國外采用宏觀、細觀和宏-細觀模型的方法對CFRP的切削機理以及切削參數的影響進行了細致研究。其中，Xu等[3-5]建立了CFRP/Ti的正交切削模型，從纖維角、切削順序及摩擦系數等對切削過程進行了研究。國內多是從事單一材料的切削研究[6-7]，相較于單一材料切削仿真研究，由于疊層材料的切削仿真存在復雜的接觸行為和網格控制，進而CFRP/Al疊層材料數值仿真切削過程不容易收斂。

本文首先將CFRP/Al疊層材料鉆削過程簡化，得到疊層材料二維正交切削模型，建立宏觀仿真模型，并與實驗對比，驗證了模型的準確性。同時研究了切削順序、進給速度、刀具前角對切削過程中切削力和CFRP切削損傷的影響規律。

1 二維正交切削有限元模型

1.1 材料性能和失效準則

單向CFRP為各向異性材料，在二維情況下，屬于平面應力問題，采用2D HASHIN失效模型[8-9]來描述單向CFRP材料的失效,如下式所示：

(1)

(2)

(3)

(4)

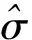
單向CFRP的材料參數[10]如表1所示。

表1 單向CFRP材料參數

表2 單向CFRP損傷參數 MPa

鋁合金材料型號為Al 2024-T351，其材料參數如表3所示[11]。

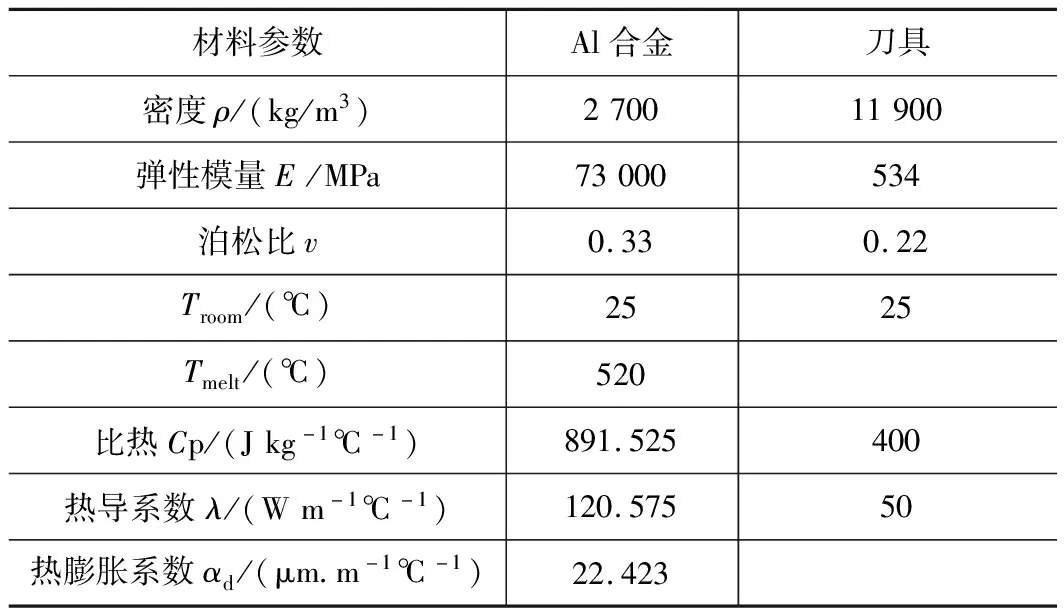
表3 Al 2024-T351和刀具材料參數

采用基于經驗的J-C本構關系模型[12]，如下式所示：

(5)

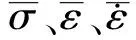
同時采用J-C剪切破壞模型[12]與損傷起始準則相對應，如下式所示：

(6)

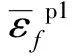
表4 Al 2024-T351 J-C參數

失效參數為：d1=0.13、d2=0.13、d3=-1.5、d4=0.011、d5=0。

1.2 有限元模型建模關鍵步驟

將疊層材料鉆削過程簡化為二維正交切削過程[3,13],如圖1所示。由于疊層材料有CFRP→Al合金、Al合金→CFRP兩種鉆削順序，因此正交切削模型也有兩種切削順序，如圖1a、b所示。

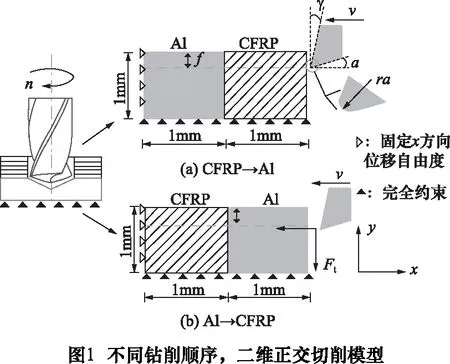
切削仿真采用商用ABAQUS軟件，運用EXPLICIT模塊以及拉格朗日網格控制算法。工件的尺寸為2 mm×1 mm，邊界條件如圖1所示，下邊界完全約束，左邊界固定x方向位移自由度。單向CFRP采用宏觀建模，將截面屬性定義為均質實體，并賦予材料方向即可。刃口半徑ra=0.01 mm，同時為減小運算時工件應力的突然增大，刀具在距離工件0.01 mm處開始切削。

單向CFRP采用平面應力線性插值單元CPS4R，網格尺寸為0.01 mm。Al 2024-T351采用溫度-位移耦合單元CPE4RT，在損傷演化過程中，使用拉伸和剪切混合模式下的斷裂能量來用于金屬材料去除的仿真。刀具采用CPE3T單元。

由于材料結合區對CFRP/Al切削力的產生和切屑分離等的影響較小，因此兩種材料之間通過“綁定”進行連接[3]。采用庫倫定律來描述刀具與材料之間的接觸摩擦行為，刀具與單向CFRP之間摩擦系數為0.4[4]、與Al 2024-T351之間的摩擦系數為0.1[14]。

2 有限元模型驗證

2.1 單向CFRP有限元模型驗證

采用與文獻[10]相同的加工環境來進行模型驗證，切削速度Vc為6 m/min，進給速度f為0.2 mm/r，刀具前角γ為0°，后角α為7°。實驗與仿真在平均切削力Fc之間的誤差如表5所示。

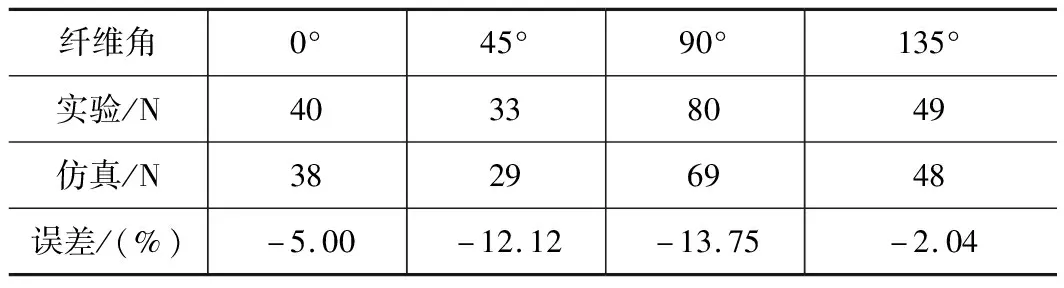
表5 不同纖維角，實驗與仿真平均切削力Fc誤差

從表5中可知，仿真與實驗最大誤差為-13.75%，最小為-2.04%，且仿真數據小于實驗數據，實驗與仿真結果具有較強的相關性。

不同纖維角的單向CFRP切屑形態，仿真與實驗對比如圖2所示。

從圖2可知，不同纖維方向角的切屑仿真與實驗有較好的一致性，且應力沿纖維方向分布。因此該模型能夠有效模擬單向CFRP的切削過程。

2.2 Al 2024-T351有限元模型驗證

采用與文獻[11]相同的加工環境來進行模型驗證，切削速度為200/400/800 m/min，進給速度為0.4 mm，前角γ為0°，后角α為7°，切削厚度αp為4 mm。實驗與實仿真在平均切削力Fc之間的誤差如表6所示。

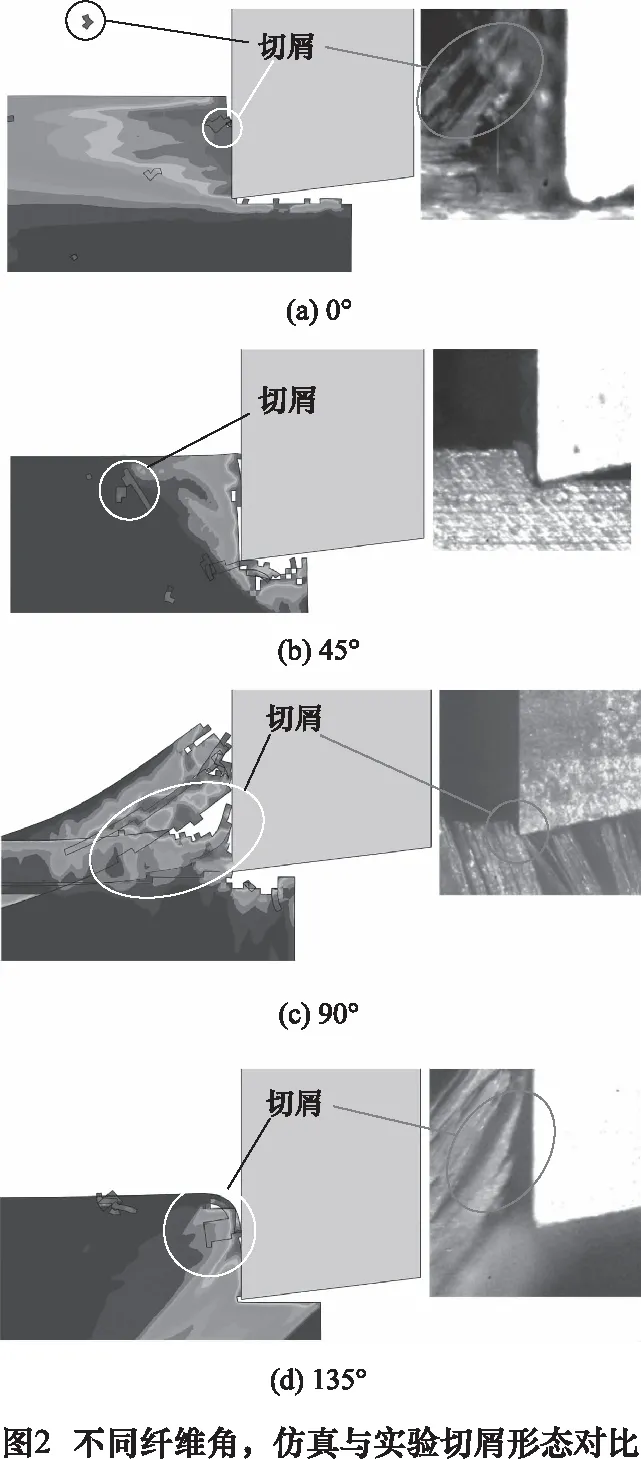
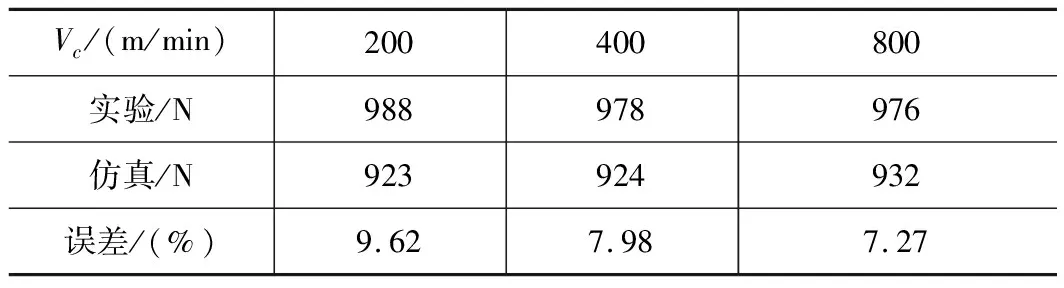
表6 不同切削速度，實驗與仿真平均切削力Fc誤差

從表6中可知，仿真與實驗最大誤差為9.62%，最小為7.27%，且仿真數據大于實驗數據，實驗與仿真結果具有較強的相關性。

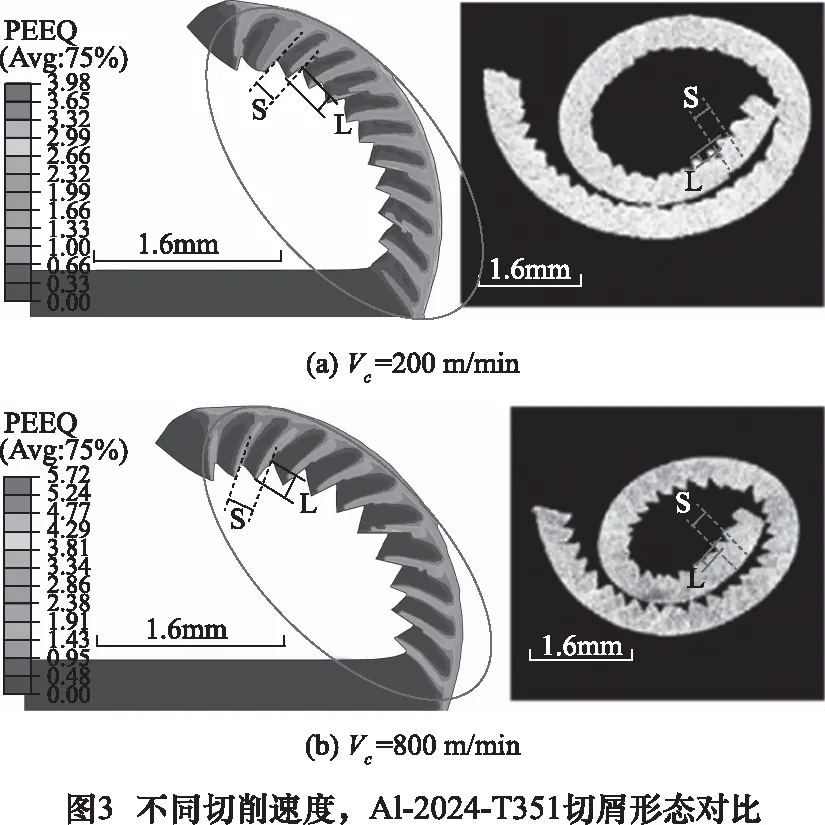
不同切削速度，仿真與實驗的切屑形態對比如圖3所示。

圖3為不同切削條件下仿真和實驗的切屑形態，測量了仿真的切屑從第3鋸齒到第8鋸齒之間的平均鋸齒高度L和平均剪切帶寬度S。

當Vc為200 m/min時,L=0.123 mm、S=0.198 mm;當Vc為800 m/min時,L=0.150 mm、S=0.243 mm。Vc越大鋸齒化程度越大，仿真與實驗的鋸齒形形態與彎曲半徑有較好的一致性。

因此該模型能夠有效模擬Al 2024-T351的切削過程。

3 仿真結果分析

3.1 切削順序對切削過程影響分析

采用45°纖維角[15]的工件，前角γ為20°、后角α為7°的刀具參數，切削速度Vc為60 m/min，進給速度f為0.2 mm/r的切削參數。CFRP→Al、Al→CFRP兩種切削順序對平均切削力Fc和平均切削力Ft影響如圖4所示。

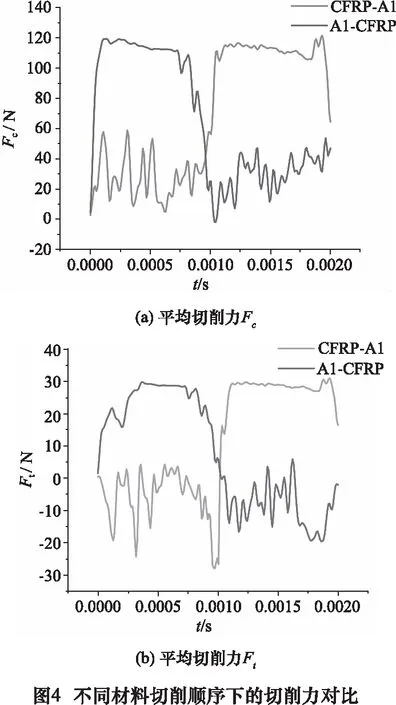
從圖4可得，疊層材料在材料過渡階段切削時，切削力存在一個突變的過程。切削Al合金部分時的切削力的穩定性遠高于切削單向CFRP部分的切削力。Al→CFRP切削順序時的單向CFRP部分的切削力Fc高于CFRP→Al順序時的切削力Fc。

不同切削順序切削過程如圖5所示。單向CFRP切削損傷以切削加工后表面損傷深度來描述，定義為纖維最大拉伸損傷(HSNFCCRT)深度到加工后的表面之間的距離h，如圖5所示。

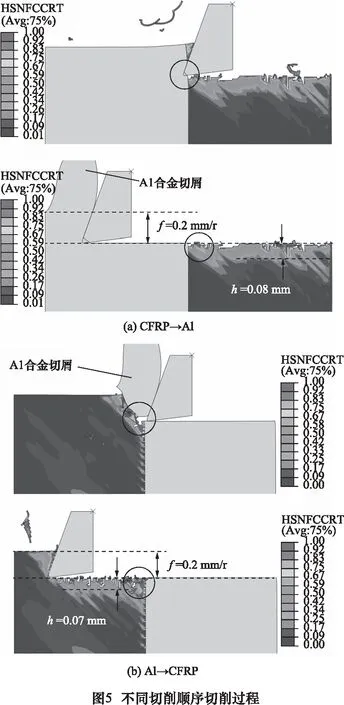
從圖5可得，CFRP→Al切削順序時，切削損傷深度h=0.08 mm，Al→CFRP切削順序時，h=0.07 mm，但在過渡區域的纖維拉伸損傷嚴重，如圖5圈出區域所示。

采用Al→CFRP切削順序，在材料過渡階段切削時，Al合金切屑還未來得及分離，切屑粘附在前刀面上，形成負前角，并代替前刀面進行切削，單向CFRP切屑流動受阻，切削阻力增大，纖維拉伸損傷嚴重。

因此采用CFRP→Al的切削加工順序好于Al→CFRP。

3.2 進給速度、刀前角對切削過程影響分析

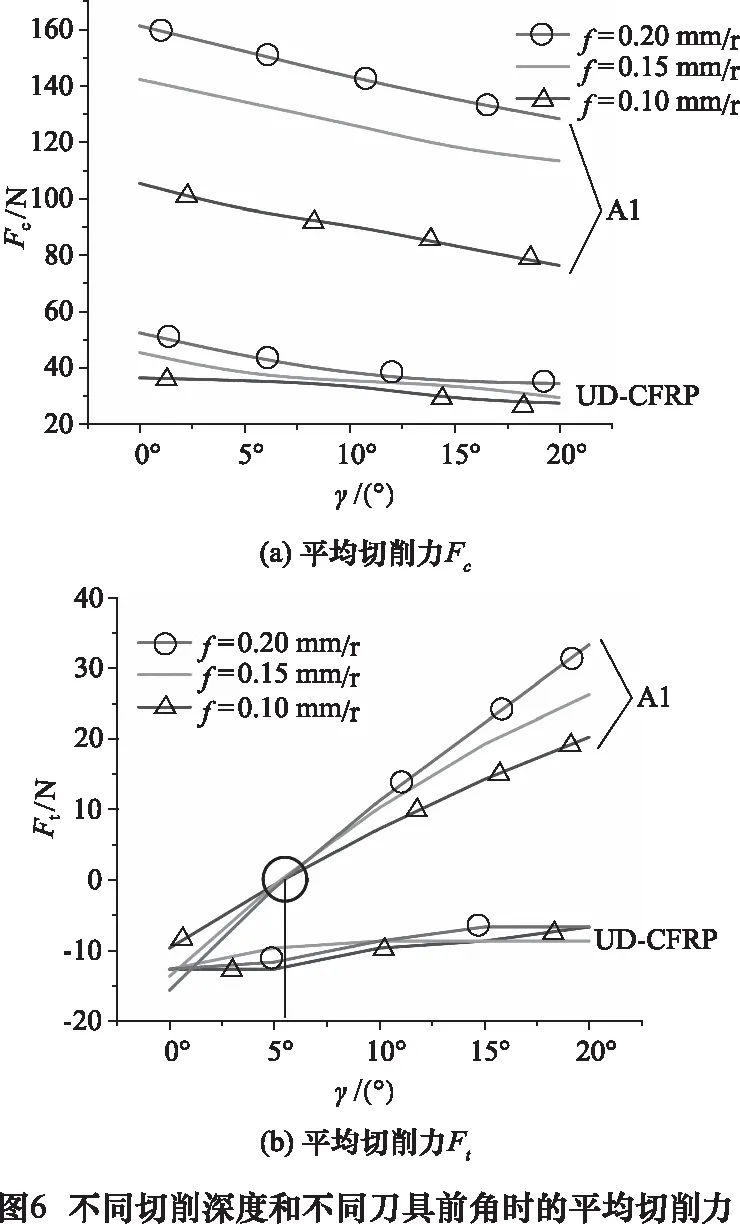
采用CFRP→Al切削順序、后角α為7°、切削速度為Vc為60 m/min。采用進給速度f為0.1/0.15/0.2 mm/r的切削參數，刀具前角α為0°/5°/10°/15°/20°的刀具結構參數，來分析切削參數和刀具結構參數對疊層材料二維正交切削過程中切削力的影響。在不同進給速度和不同刀具前角時，切削過程的平均切削力Fc、Ft如圖6所示。

利用多元非線性回歸法建立進給速度和刀具前角對切削力的經驗預測模型，如下式：

單向CFRP部分：

Fc=89.663f0.358γ-0.238

(7)

Ft=-10.935f0.105γ-0.323

(8)

Al合金部分：

Fc=449.56f0.653γ-0.146

(9)

Ft=89.663f0.703γ2.636

(10)

從圖6和切削力的經驗預測模型可得，在疊層材料切削過程中，進給速度和刀具前角對單向CFRP部分切削力的影響小于Al合金部分切削力。進給速度f對切削力Fc的產生有顯著影響，f的少量增加導致疊層材料切削力Fc的大幅提升。隨著刀具前角的增大，切削力Fc減小。

從圖6b可得，進給速度和刀具前角對單向CFRP部分切削力Ft的影響不明顯。在切削Al合金時，隨著刀具前角的增大，在進給方向的切削力Ft先減小后增大，當其為6°時，切削力Ft最小。

切削損傷主要針對于單向CFRP。當進給速度f=0.2 mm/r時，單向CFRP在不同刀具前角時的加工后表面損傷深度，如圖7所示。

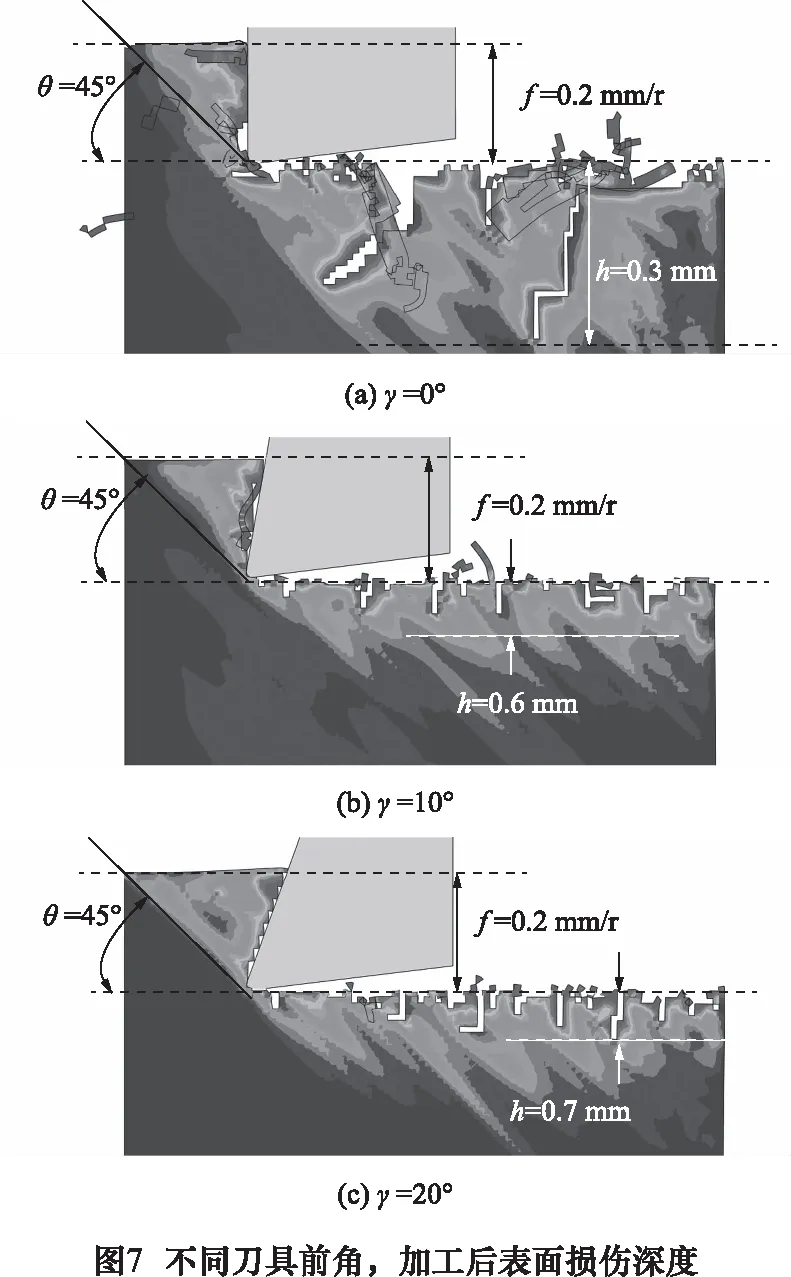
在不同進給速度、不同刀具前角時，切削加工后切削損傷深度如圖8所示。

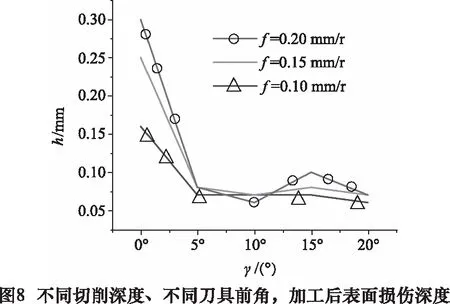
由于采用不同切削工藝參數，在切削各向異性的單向CFRP材料時將會產生不同切削力，同時由于構成單向板的單根碳纖維絲束的切斷力為一定值，因此在不同切削力作用下，單向CFRP切削加工后表面將出現不同程度的損傷。從圖6a和圖8可得，影響切削損傷的切削力為Fc，但當刀具前角α大于5°時，進給速度f和前角α對45°單向CFRP的切削力和加工后表面損傷影響不顯著。

利用多元非線性回歸法建立進給速度和刀具前角對切削加工后表面損傷深度h的經驗預測模型，如下式：

h=0.173f-1.033γ0.432

(11)

從預測模型可得，進給速度對單向CFRP加工后表面損傷的程度遠大于刀具前角。

4 結語

(1)將CFRP/Al疊層材料鉆削過程中的刀具結構進行簡化，建立其二維正交切削宏觀有限元模型。與實驗對比，CFRP部分模型與實驗之間切削力的最大誤差為13.75%，Al合金部分的最大誤差為9.62%，同時切屑形態也有較好的一致性，該模型具有較高的精確度。

(2)在CFRP/Al疊層材料的切削加工過程中，需要考慮加工順序對切削過程的影響。在二維切削情況下，CFRP→Al的切削順序優于Al→CFRP的切削順序，能夠產生較小的切削力和CFRP切削后表面損傷。

(3)利用多元非線性回歸法建立了CFRP/Al疊層材料切削時進給速度和刀具前角對切削力和切削損傷的經驗預測模型。從模型可得，進給速度f對切削力和切削損傷的產生有顯著影響，同時Al合金部分切削力受進給速度和刀具前角影響高于對單向CFRP部分切削力的影響。

(4)當刀具前角α大于5°時，增大刀具前角對45°單向CFRP的切削力和加工后表面損傷影響不顯著。