正應力作用下北山花崗巖單裂隙幾何特征對輻射流滲流行為的影響研究

范棟玨，趙星光，張海洋，劉 健，劉飛楊

(核工業(yè)北京地質(zhì)研究院，北京 100029)

地下巖體中存在大量的天然裂隙，構(gòu)成了地下水滲流的潛在通道。地下水滲流可能會導致采掘過程中圍巖突水或支護失效。因此，研究裂隙巖體的滲流特性對地下工程安全具有重要意義。地下水在裂隙中的流動形態(tài)可分為平行流和輻射流[1]，通常地下水從裂隙一側(cè)向另一側(cè)以平行流方式流動，但對地下工程結(jié)構(gòu)進行開挖時，地下水以輻射流方式從巖體四周流向臨空面。因此，輻射流行為是裂隙滲流特性的研究重點之一。

早期，學者們將天然裂隙簡化為平行且互相不接觸的平板，并將Navier-Stoke方程簡化后建立了立方定理[2]。然而，天然裂隙表面粗糙不平，且存在點接觸或面接觸，其接觸面積隨應力的增加而增大[3]，若采用傳統(tǒng)的立方定理計算將高估裂隙的滲透性能。為了合理描述裂隙滲流行為，許多學者結(jié)合室內(nèi)裂隙滲流試驗結(jié)果對立方定理進行了修正。王媛等[4]將立方定理的修正方法分為五類：粗糙性修正系數(shù)修正法、隙寬密度分布函數(shù)修正法、隙寬分布函數(shù)直接修正法、節(jié)理粗糙度系數(shù)JRC修正法以及面積接觸率修正法；還有學者[5-8]通過引入等效水力隙寬、平均隙寬、力學隙寬等參數(shù)，減少了立方定律帶來的誤差。此外，許多學者[6,9-15]針對裂隙力學隙寬與等效水力隙寬，結(jié)合接觸面積、隙寬分布影響系數(shù)建立了相應的裂隙滲流計算模型。然而，這些計算模型中采用的隙寬分布影響系數(shù)并不能完全表征裂隙內(nèi)隙寬大小及其非均勻分布對裂隙滲流特性的影響。

對于單裂隙輻射流，BARKE[1]建立了廣義輻射流(GRF)模型，描述了常用液壓測試形式中的水頭變化；CAO等[16]針對輻射流平行板模型提出了修正的立方定率公式，減小了由立方定理計算帶來的誤差。 然而，目前關(guān)于裂隙輻射流滲流特性研究較少，特別是對于輻射流條件下的滲流計算模型鮮有研究。 因此，本文根據(jù)裂隙形貌掃描結(jié)果，采用地質(zhì)統(tǒng)計學中變異函數(shù)理論對裂隙空隙三維分布進行量化表征。同時，考慮裂隙空隙三維分布特征和接觸率為影響因素，提出輻射流等效水力隙寬計算模型，并使用MTS815巖石力學試驗系統(tǒng)對裂隙巖樣進行不同正應力下的滲流試驗，驗證計算模型的合理有效性。

1 裂隙滲流特性試驗研究

1.1 巖樣加工制備

巖樣取自我國高放廢物處置庫北山預選區(qū)新場巖體BS33號鉆孔附近淺地表。首先，加工4個直徑為100 mm、高度為100 mm的圓柱形巖樣；然后，將巖樣放入劈裂裝置中(圖1(a))，采用壓力機以1 500 N/s的加載速率對巖樣進行劈裂，形成人工裂隙；最后，采用水射流切割設備在下部巖樣中心打一個小孔，作為平面徑向流的中心進水邊界，在上部巖樣距離側(cè)面邊界8 mm處均勻打一圈小孔，并沿小孔打出與界面同心的圓形溝槽作為出水邊界(圖1(b))。

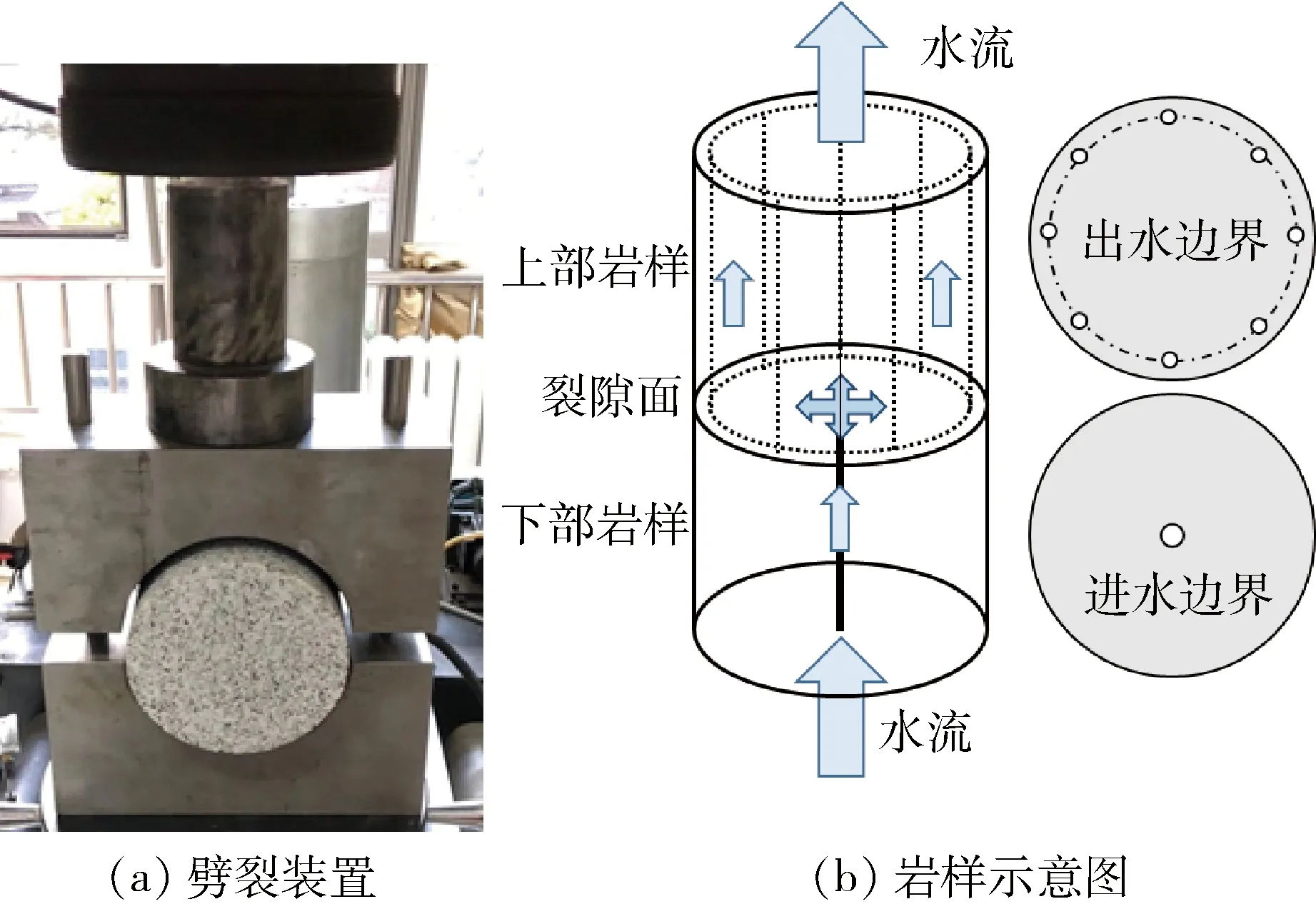
圖1 裂隙巖樣示意圖Fig.1 Schematic diagram of fracture specimen

1.2 試驗方法

采用MTS815巖石力學試驗系統(tǒng)對裂隙巖樣進行不同正應力下的輻射流試驗(圖2(a))。首先，使用硅膠密封裂隙巖樣的側(cè)縫(圖2(b))，待硅膠干燥后利用熱縮管將巖樣與試驗機壓頭緊密包裹，并將軸向引伸計安裝于巖樣中部測量裂隙加載過程中的變形(圖2(c))。 隨后，對巖樣施加10 MPa圍壓，以有效避免水從巖樣側(cè)壁與熱縮管之間的縫隙內(nèi)流動。 最后，采用不同的正應力(11 MPa、15 MPa、20 MPa、30 MPa、40 MPa、50 MPa、60 MPa)對巖樣進行分級加載，加載過程如圖3所示。 分別在每一級荷載作用下采用穩(wěn)態(tài)法測量輻射流流量。 在試驗過程中，進水口與出水口水壓差恒定為1 MPa，進口流量、出口流量由活塞泵位移與穩(wěn)定滲流時間計算獲得。

圖2 滲流試驗設備及巖樣安裝Fig.2 Seepage test equipment and a typical specimen setup

圖3 正應力加載過程Fig.3 Normal stress loading process

1.3 巖石裂隙滲流特性分析

根據(jù)上述試驗方案，獲得了不同正應力作用下水在裂隙巖樣中的流量變化，如圖4所示。由圖4可知，在正應力為11～60 MPa范圍內(nèi)，所有巖樣流量隨正應力的增大表現(xiàn)出相似的變化規(guī)律，即流量隨正應力的增大而減小，且其衰減速率隨正應力增加而減小，表明水在裂隙中的流量變化對低正應力條件(<20 MPa)較為敏感；當正應力大于50 MPa時，各巖樣流量值的差異性不再顯著。此外，在相同正應力條件下，巖樣3的流量顯著高于其他巖樣，即裂隙內(nèi)部幾何特征存在差異性，致使其表現(xiàn)出了不同的滲流特性。因此，本文對裂隙空隙三維分布進行分析和表征，查明裂隙內(nèi)部幾何特征對其滲流性能的影響規(guī)律。

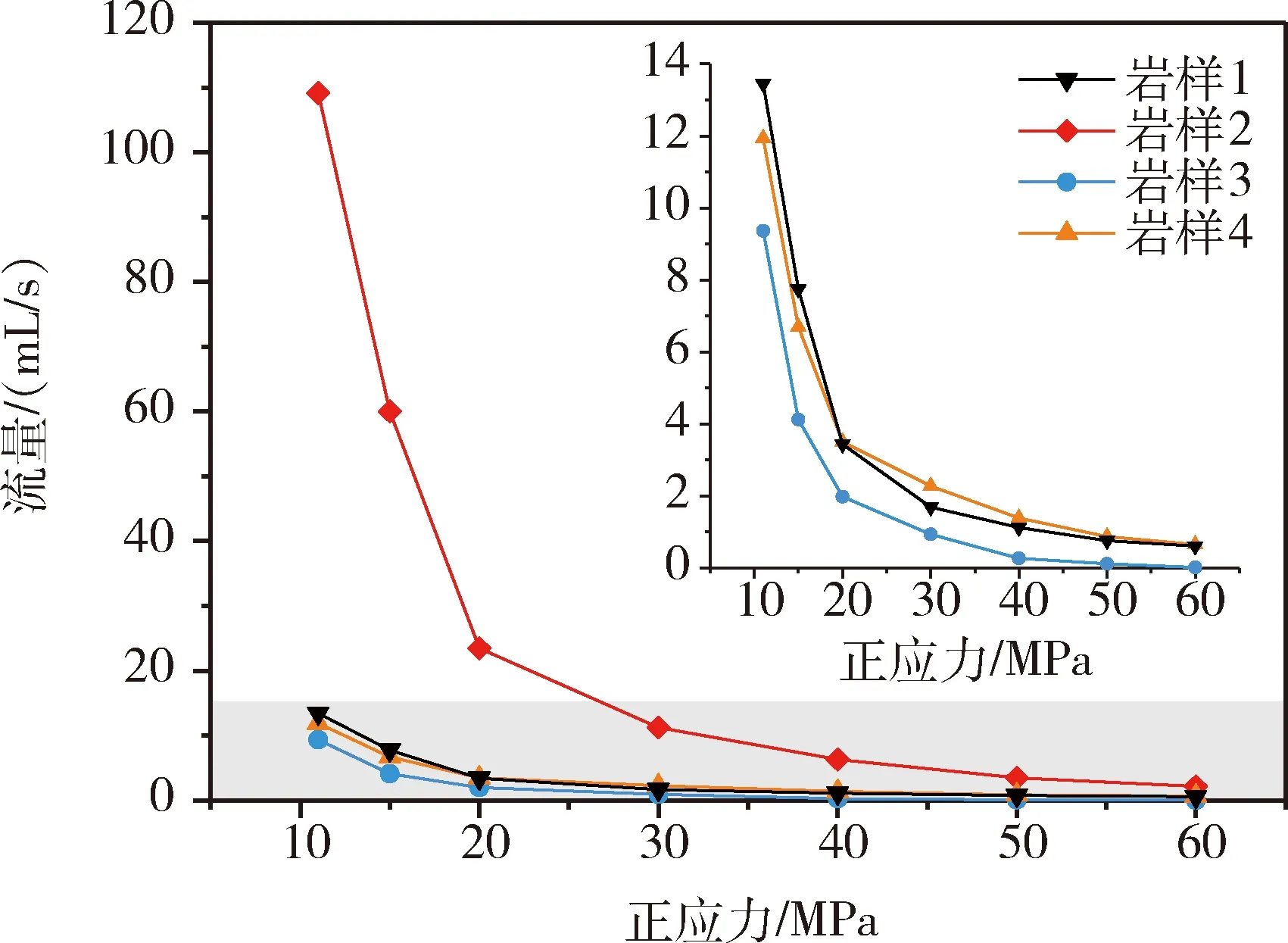
圖4 裂隙巖樣流量隨正應力的變化Fig.4 Variations of flow quantity with normal stressfor the fracture specimens

2 裂隙內(nèi)部幾何特征量化表征

巖石裂隙中存在大量空腔及接觸域，它們是影響裂隙滲流特性的關(guān)鍵因素。根據(jù)HAKAMI[17]的研究，裂隙內(nèi)部幾何特征主要包括裂隙隙寬、裂隙接觸區(qū)域、裂隙內(nèi)部空隙三維分布等。其中，裂隙隙寬可由等效水力隙寬、平均隙寬、力學隙寬等參數(shù)進行表征[5-8]，裂隙接觸區(qū)域可由接觸率進行表征。 然而，對裂隙內(nèi)部空隙三維分布特征表征參數(shù)的研究較少。PYRAK等[18]對裂隙內(nèi)部的隙寬分布進行研究，發(fā)現(xiàn)裂隙隙寬分布通常服從正態(tài)分布或?qū)?shù)正態(tài)分布，但其分布函數(shù)無法表示裂隙連通以及裂隙非均勻變化對滲流的影響；陳躍都[19]采用相對分形維數(shù)對裂隙隙寬的分布進行表征，但其使用的盒子計數(shù)法不適用于圓柱形的輻射流試件。因此，本文根據(jù)裂隙面掃描結(jié)果，采用變異函數(shù)理論對裂隙空隙三維分布特征進行表征，并結(jié)合裂隙力學隙寬和接觸率參數(shù)，對裂隙內(nèi)部幾何特征參數(shù)進行量化表征。

2.1 裂隙面形貌特征掃描

為了獲得裂隙面的形貌特征，在試驗前后采用OKIO-5M三維形貌掃描儀對裂隙面進行掃描(圖5(a))，掃描精度為10 μm，典型掃描結(jié)果如圖5(b)所示。通過三維點云處理軟件，采用克里金法[20]將獲得的裂隙面三維點云離散在x-y平面上形成等間距的規(guī)則點云，并將裂隙上下表面的點云坐標劃分成規(guī)則網(wǎng)格，且上下裂隙面網(wǎng)格相互對應，以便對裂隙幾何特征參數(shù)進行計算。隨后，采用點云拼接法[18]計算裂隙各網(wǎng)格點處隙寬ei，定義裂隙隙寬ei≤0的網(wǎng)格點為接觸點，裂隙隙寬ei>0的點為空隙點，即可獲得裂隙間的空隙及接觸域的分布大小。

圖5 三維形貌掃描設備及裂隙典型掃描結(jié)果Fig.5 3D shape scanner and typical scanning results

2.2 裂隙空隙三維變異函數(shù)計算

作為地質(zhì)統(tǒng)計學的基本工具，變異函數(shù)既能描述區(qū)域變量的空間結(jié)構(gòu)，也能描述其隨機性。變異函數(shù)r(h)定義為區(qū)域化變量的增量平方的數(shù)學期望，即區(qū)域化變量的方差[21]，見式(1)。

2r(h)=E{[Z(X+h)-Z(X)2]}

(1)

式中：h為數(shù)據(jù)點間距離；Z(X)、Z(X+h)分別為空間某點位置X和與之相距h的兩個區(qū)域變化量。

將掃描獲得的裂隙間空隙ei作為區(qū)域變量即可計算裂隙隙寬分布變異函數(shù)。由于輻射流條件下，裂隙內(nèi)流體流動方向存在不確定性，可用三維經(jīng)驗變異函數(shù)r*(h)[22]進行估算，即以h為相隔的任意對點的隙寬值[e(xi+a,yi+b)，e(xi,yi)]間增量平方的算數(shù)平均值進行計算，見式(2)。

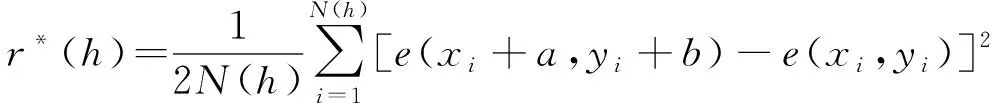
(2)

式中：N(h)為有效數(shù)據(jù)對數(shù)；e(xi,yi)為點云在(xi,yi)處的隙寬值；a、b為h在x方向、y方向上的分量，即a2+b2=h2。

為獲得裂隙隙寬的變異特征，并對裂隙隙寬的三維分布進行統(tǒng)計計算，需要對變異函數(shù)散點圖進行擬合，進而獲得變異函數(shù)的理論模型及其參數(shù)。常見的變異函數(shù)理論模型有球狀模型、指數(shù)模型、對數(shù)模型等。利用式(2)獲得巖樣1在無應力狀態(tài)下裂隙隙寬變異函數(shù)曲線如圖6所示。

圖6 變異函數(shù)曲線Fig.6 Variogram curve

從圖6中可以看出，曲線前段增長較快，中后段水平上下波動，可選取球狀模型(式(3))進行擬合。

(3)

需要說明的是，變異函數(shù)出現(xiàn)第一個峰值點之后的數(shù)據(jù)是大于變程a的數(shù)據(jù)，與函數(shù)擬合無關(guān)[23]。因此，擬合對象僅選擇變異函數(shù)的第一個峰值點之前的r*(h)值。

2.3 裂隙內(nèi)部幾何特征量化表征參數(shù)計算

獲得裂隙空隙的變異函數(shù)擬合曲線后，即可采用相關(guān)參數(shù)對裂隙空隙的三維分布特征進行表征。變異函數(shù)球狀模型主要參數(shù)有變程a、基臺值C和塊金系數(shù)C0。 獲得的塊金系數(shù)C0一般較小，在0左右波動，對變異函數(shù)形式影響不大，因此不作考慮。基臺C表示隙寬隨空間變化的幅度，通常基臺C越大，隙寬隨空間變化幅度越大。 變程a表示隙寬隨空間變化的頻率，通常變程a越大，隙寬隨空間變化的頻率越大，隙寬變化曲線就越平緩。 因此，裂隙隙寬的不均勻程度與基臺C成正比，與變程a成反比。本文提出裂隙空隙的三維分布系數(shù)CA來對裂隙空隙的三維分布特征進行量化表征，其表達式見式(4)。

CA=C2×a-1

(4)

由式(4)可以看出，裂隙空隙的三維分布系數(shù)CA值較大時，基臺C或變程a的值較大，此時裂隙空隙隨空間的分布不均勻。當CA=0時，裂隙上下表面完全平行，裂隙空隙均勻分布。

根據(jù)裂隙面掃描結(jié)果，采用點云拼接法[19]計算裂隙在不同應力作用下力學隙寬en和接觸率ω。以力學隙寬en為空間變量，采用變異函數(shù)理論獲得基臺C與變程a，并根據(jù)式(4)計算裂隙空隙的三維分布系數(shù)CA，見表1。

表1 變異函數(shù)計算結(jié)果Table 1 Fitting results of average aperture

3 輻射流滲流模型建立

目前，單裂隙滲流的研究重點是針對裂隙力學隙寬與等效水力隙寬建立相應的計算模型[6,9-15]，其中應用最為廣泛的為YEO[14]建立的模型，見式(5)。

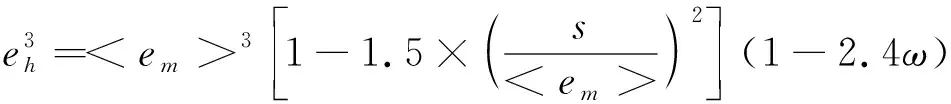
(5)

式中：為裂隙隙寬的平均值，m；s為裂隙隙寬的標準偏差；ω為裂隙的接觸率。

YEO模型中(1-2.4ω)和[1-1.5(s/)2]分別代表接觸率和裂隙隙寬對裂隙水力學開度的影響。然而，該模型中的裂隙隙寬標準偏差s僅代表裂隙隙寬分布的分散程度，并不能完全表征裂隙內(nèi)隙寬大小及其非均勻分布對裂隙滲流特性的影響。同時，該模型夸大了裂隙接觸率對水力隙寬計算的影響。例如，當裂隙接觸率大于0.416時，其接觸率影響系數(shù)(1-2.4ω)小于0，導致裂隙等效水力為負值，即表明裂隙不具有滲透性，與實際不符。

因此，本文在YEO模型的基礎(chǔ)上，對其接觸率影響系數(shù)進行修正，并使用力學隙寬和空隙三維分布系數(shù)來代表裂隙隙寬及對其三維分布的影響，提出了CA計算模型見式(6)。

(6)

式中，n為試驗擬合參數(shù)，對于本試驗采用的北山花崗巖裂隙巖樣，n=5.9。

為驗證CA模型的有效性，將表1中裂隙幾何特征參數(shù)代入式(6)，獲得等效水力隙寬值。隨后，采用立方定理計算裂隙流量。考慮到輻射流的擴散特性，使用輻射流立方定理計算[14]，見式(7)。

(7)

式中：Q為流體流量，m3/s；r0和r1分別為巖樣內(nèi)圈半徑和外圈半徑；ΔH為水頭差，m；ν為水的運動黏度，m2/s。將裂隙流量實測值與CA模型計算值進行對比，如圖7所示。

圖7 各巖樣CA模型計算值和試驗結(jié)果對比Fig.7 Comparison of calculated values of CA models and test results for different samples

從圖7中可以看出，采用CA模型獲得的裂隙等效水力隙寬與實測值較為接近，由此表明該模型可以合理地描述裂隙幾何特性對裂隙滲透特性的影響。此外，對于線性達西滲流而言，其滲透率k與水力隙寬eh存在定量關(guān)系，見式(8)。

(8)

將式(6)代入式(8)可得滲透率的幾何特征定量表達式，見式(9)。

(9)

對于光滑平行板模型，其接觸率ω和裂隙連通空隙三維分布表征系數(shù)CA均為0，此時eh=en,式(9)便可簡化為式(8)。需要說明的是，該模型的所有參數(shù)是在室內(nèi)巖樣尺度上獲得，對于其尺寸效應還需進一步研究。

4 結(jié) 論

1) 水在裂隙巖樣中的流量隨正應力的增大而減小，且其衰減速率隨正應力增加而減小。

2) 基于變異函數(shù)理論對裂隙空隙三維分布進行量化表征，建立了輻射流等效水力隙寬計算模型(CA模型)。該模型考慮了裂隙幾何特征對裂隙滲透特性的影響，可定量表征正應力作用下裂隙等效水力隙寬與力學隙寬、凸起接觸率和空隙三維分布系數(shù)之間的函數(shù)關(guān)系，模型計算結(jié)果與試驗結(jié)果具有較好的一致性。

由于室內(nèi)試驗條件的限制，本文尚未對更大尺寸的巖石裂隙進行試驗。此外，現(xiàn)有手段也無法獲取流體在裂隙內(nèi)的流動軌跡。因此，裂隙輻射流的尺寸效應及滲流軌跡對其滲流特性的影響是下一階段的研究重點。