HOMOCLINIC SOLUTIONS OF NONLINEAR LAPLACIAN DIFFERENCE EQUATIONS WITHOUT AMBROSETTI-RABINOWITZ CONDITION?
University of Palermo,Department of Mathematics and Computer Science,Via Archirafi 34,90123,Palermo,Italy
E-mail:antonella.nastasi@unipa.it
Stepan TERSIAN
Institute of Mathematics and Informatics,Bulgarian Academy of Sciences,1113 Sofia,Bulgaria
E-mail:sterzian@uni-ruse.bg
Calogero VETRO?
University of Palermo,Department of Mathematics and Computer Science,Via Archirafi 34,90123,Palermo,Italy
E-mail:calogero.vetro@unipa.it
Abstract The aim of this paper is to establish the existence of at least two non-zero homoclinic solutions for a nonlinear Laplacian difference equation without using Ambrosetti-Rabinowitz type-conditions.The main tools are mountain pass theorem and Palais-Smale compactness condition involving suitable functionals.
Key words Difference equations;homoclinic solutions;non-zero solutions;(p,q)-Laplacian operator
1 Introduction
This paper is motivated by some manuscripts concerning with the nonlinear Laplacian difference equations.Here,we consider the boundary value problem
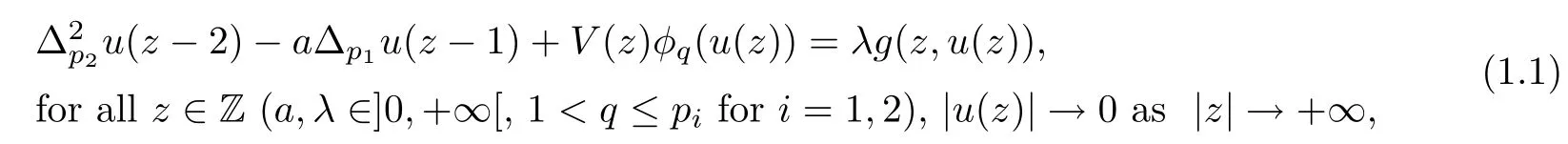
driven by q-Laplacian type operator φq(u)=|u|q?2u with u∈R.In(1.1)we use the following notations:
?Δu(z?1)=u(z)?u(z?1)is the forward difference operator,
?Δ2u(z?2)=Δu(z?1)?Δu(z?2)is the second order forward difference operator,
Let V:Z→R and g:Z×R→R.We assume that the function g is continuous.Moreover,we denote by G:Z×R→R the function
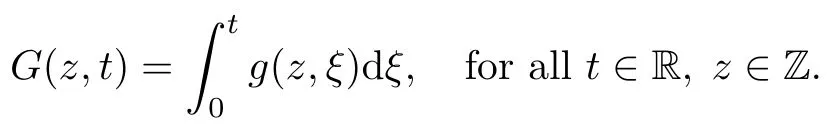
The assumptions on problem(1.1)are as follows:
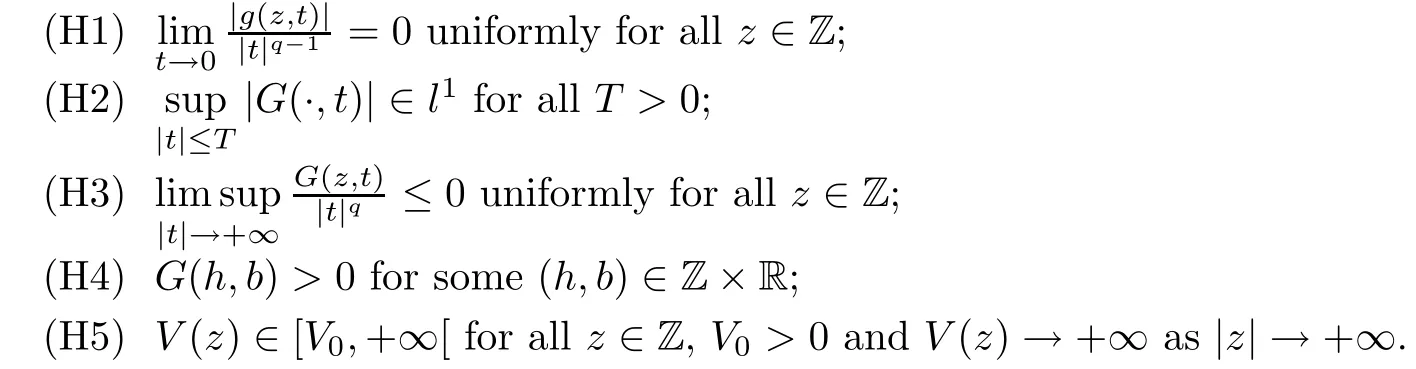
We approach problem(1.1)by using its variational formulation.We note that there is a relevant literature on differential equations driven by a q-Laplacian operator or(p1,p2)-Laplacian operator(which is the sum of a p1-Laplacian and of a p2-Laplacian).Indeed,by using specific nonlinearities(g:Z×R→R),we are able to study the dynamical behaviour of real phenomena in biological and physical settings(for more details,we refer to Diening-Harjulehto-H?st?-R?uz??cka[4]and Motreanu-Motreanu-Papageorgiou[8]).In addition,Mugnai-Papageorgiou[11]and Motreanu-Vetro-Vetro[9,10]focused on(p1,p2)-Laplacian equations with p1 On the other hand,the use of difference operators leads to discrete versions of continuous differential equations(as shown in Agarwal[1]and Kelly-Peterson[7]).This specific topic of research links mathematical analysis to numerical analysis.In particular,we think of the approximation of solutions and the study of convergence and stability.In this direction,we mention the works of Cabada-Iannizzotto-Tersian[2],Iannizzotto-Tersian[5],Jiang-Zhou[6](for discrete q-Laplacian operator)and Nastasi-Vetro-Vetro[13](for discrete(p1,p2)-Laplacian operator).Also,Cabada-Li-Tersian[3],Nastasi-Vetro[12]and Saavedra-Tersian[17]investigated the existence of homoclinic solutions(that is,solutions satisfying|u(z)|→0 as|z|→+∞). We continue this study by using the variational formulation of(1.1).Thus,we establish the existence of at least two non-zero homoclinic solutions for such a problem.Hypotheses(H1)–(H5)imply that the energy functional associated to(1.1)satisfies mountain-pass geometry and Palais-Smale compactness condition(Pucci-Serrin[16]).Here,we do not use the Ambrosetti-Rabinowitz condition(that is,there existμ>pi≥q>1 and M>0 such that 0<μG(z,t)≤g(z,t)t for all z∈Z,|t|>M).We point out that the Ambrosetti-Rabinowitz condition is a useful tool in establishing the existence of nontrivial solutions for elliptic equations driven by the Laplacian,q-Laplacian and(p1,p2)-Laplacian operators,via variational methods.Indeed,it easily ensures that the above mentioned energy functional has a mountain-pass geometry and the associated Palais-Smale property holds.The interest for our results is motivated by the fact that in many practical problems the nonlinearity g:Z×R→R does not satisfy the Ambrosetti-Rabinowitz condition(for example,g(z,t)=z?μ|t|p?2tln(1+|t|α)withμ>1 and α≥1).So,it is of a certain interest to prove the existence and multiplicity of solutions in such situations.We mention the paper of Papageorgiou-Vetro-Vetro[14],where the authors employ a weaker condition which permits the consideration of both convex and concave nonlinearities. On the same lines of Saavedra-Tersian[17]and the references therein,we denote by lqthe set of sequences u:Z→R such that So,(lq,‖·‖q)is a reflexive Banach space.Similarly,by l∞we mean the set of sequences u:Z→R such that We construct the functional Jλ:lq→R,associated to problem(1.1).Precisely,we consider the functional G:lq→R given as such that G∈C1(lq,R)and Also,we need the functional L:lq→R defined by We point out that Jλ(0)=0.By Lemma 2.2 of Saavedra-Tersian[17],the functional Jλis well defined and C1-differentiable.Moreover,its critical points are solutions of problem(1.1). Now,we consider the Banach space endowed with the norm To get our result,we have to show that the functional Jλsatisfies the Palais-Smale condition(Definition 2.1)and has the mountain-pass geometry(Theorem 2.2)that we state for our setting(X,‖·‖X). Definition 2.1Given the reflexive Banach space X and its topological dual X?,then,Jλ:X→R satisfies the Palais-Smale condition if any sequence{un}such that (i){Jλ(un)}is bounded; has a convergent subsequence. We recall the mountain-pass theorem due to Pucci-Serrin[16,Theorem 1]. Theorem 2.2Consider the reflexive Banach space X.Let Jλ∈C1(X,R)be a functional satisfying the Palais-Smale condition and suppose that there are~u∈X and positive real numbers γ1,γ2withsuch that To show that Theorem 2.2 applies to the functional Jλin(2.1),we give the following auxiliary proposition: Proposition 2.3If(H1),(H2),(H3)and(H5)hold,then Jλ:X→R is coercive and satisfies the Palais-Smale condition. ProofWe split the proof into two steps. Claim 1Jλ:X→R is coercive. To be coercive,the functional Jλhas to satisfy which tends to+∞as‖u‖X→+∞,and hence Jλhas the coercivity property. Claim 2Jλ:X→R has the Palais-Smale property. From Lemma A.0.5 of Peral[15],we derive two technical conditions.Precisely,we assume that there exists c>0 satisfying The special case(2.3)(that is,1 Therefore,taking the limit as n→+∞in(2.4),we conclude that un→u in X.Thus,Jλ:X→R satisfies the Palais-Smale condition. □ To get our goal,the following value of the parameter λ in(1.1),sayplays a crucial role.Denote where h∈Z and b∈R satisfy Hypothesis(H4). We give the existence theorem which produces two non-zero homoclinic solutions. Theorem 3.1If(H1)–(H5)hold,then problem(1.1)has two non-zero homoclinic solutions,for each λ>≥0 sufficiently large. Next,we prove that zero is not a global minimizer of Jλ.To this aim,we set=beh(eh(z)=δhzfor all z∈Z,with δhz=1 if h=z,and δhz=0 otherwise).It follows that Again passing to a subsequence if necessary,we get Example 3.2The following function g:Z×R→R satisfies Hypotheses(H1)–(H4),but does not satisfy the Ambrosetti-Rabinowitz condition: where 1<κ1 We note that the boundedness of f implies that,in establishing Assumptions(H1)and(H3),only the polynomial terms play a role.So,(H1)holds true since q<κ2(recall that we pass to the limit as t→0),and(H3)follows easily since κ1 Remark 3.3We can suppose a more general assumption(H3)′,instead of(H3): (H3)′uniformly for all z∈Z,where L>0. Then,in the proof of Claim 1(Proposition 2.3),one can fix ν∈]0,[,and in Theorem 3.1 one can take λ>max2 Mathematical Background
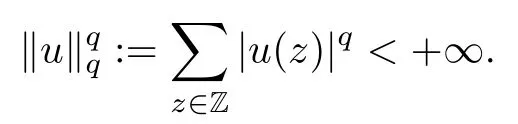
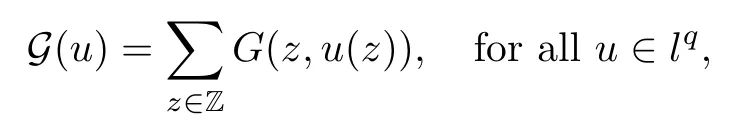
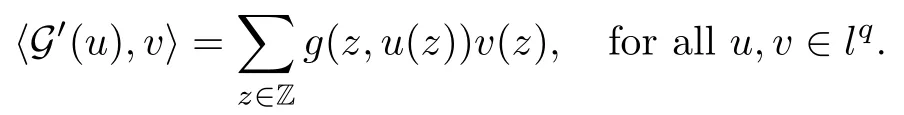
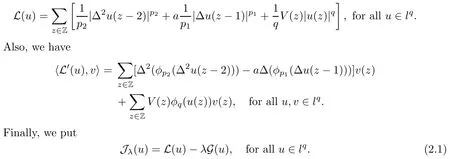
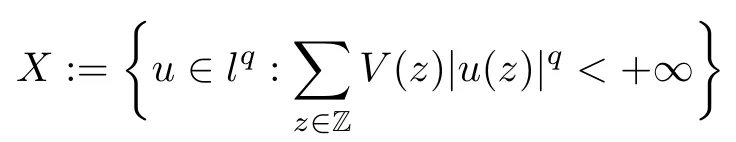
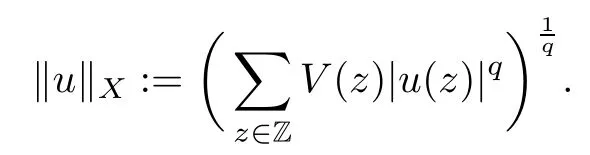
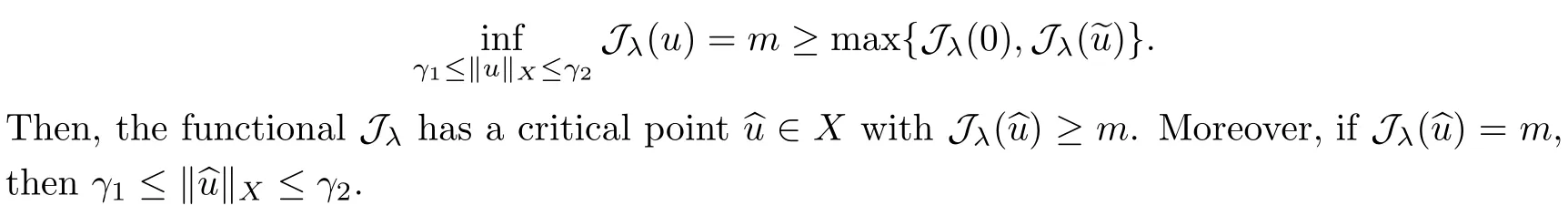
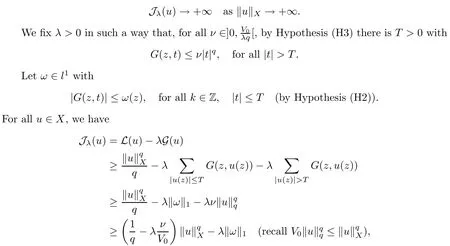

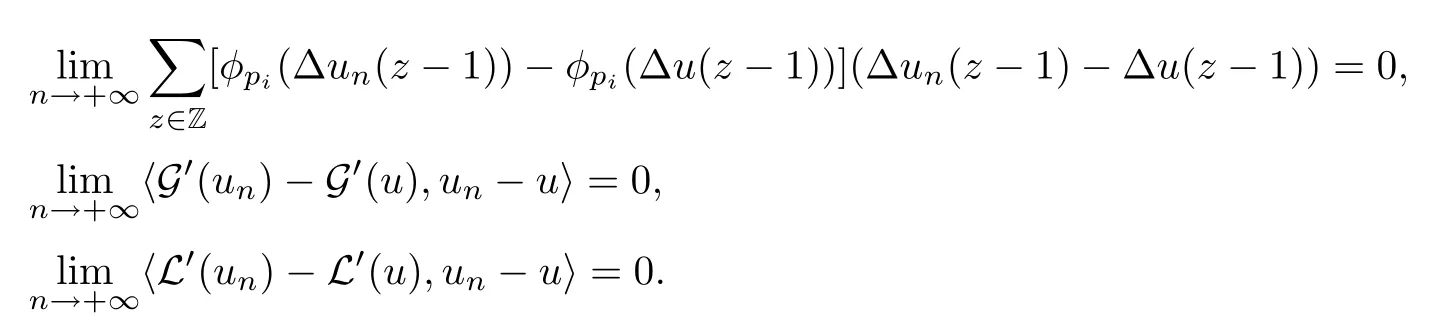
3 Main Results
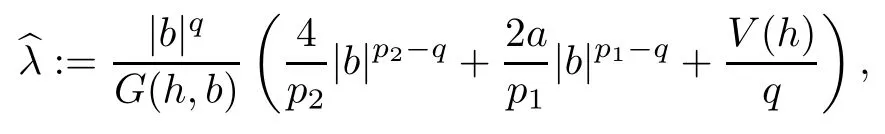



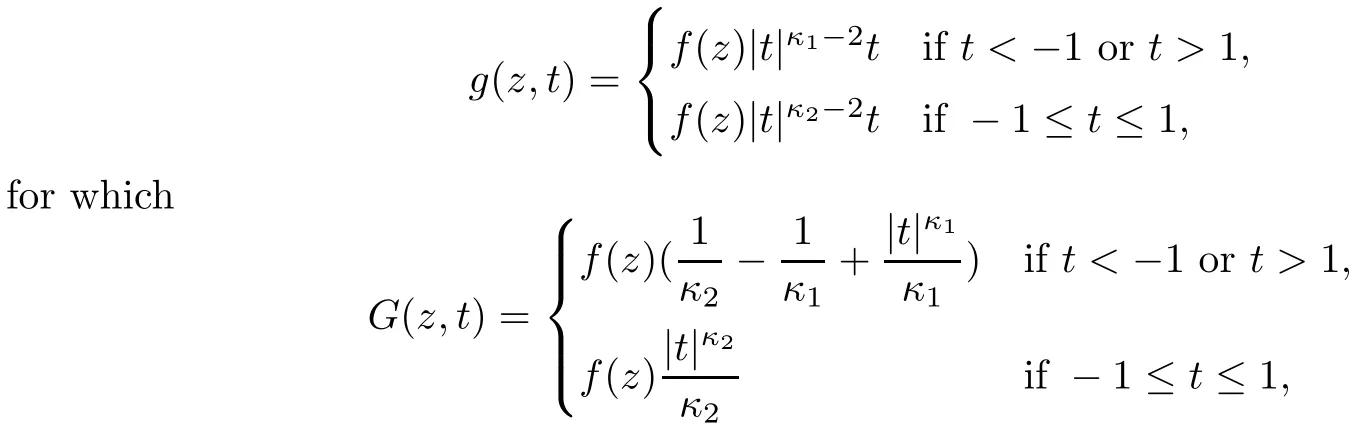
 Acta Mathematica Scientia(English Series)2021年3期
Acta Mathematica Scientia(English Series)2021年3期
