一種高性能超長點數浮點FFT加速器設計

王 諦 石 嵩 吳鐵彬 劉 亮 譚弘兵 郝子宇 過 鋒 李宏亮

(江南計算技術研究所 江蘇無錫 214083)

(wangdi_csarch＠126.com)

離散傅里葉變換(discrete Fourier transform,DFT)作為時域和頻域轉換的基本運算,在數字信號處理中占據核心地位[1],應用領域十分廣泛.快速傅里葉變換[2](fast Fourier transform,FFT)是DFT的快速算法,FFT的提出促進了數字信號處理的發展,被評選為20世紀科學和工程界最具影響力的十大算法之一[3].隨著高速采樣和實時信號處理技術的發展,高性能超長點數FFT的需求迅速增長[4].由于FFT的算法復雜度為O(NlgN),FFT和以FFT為基礎的各類時-頻變換算法的計算占比愈發凸顯.例如,在國際大科學工程——平方公里陣列(square kilometer array,SKA)射電望遠鏡項目中,FFT的計算占比達40%[5].目前已有FFT計算架構的最大吞吐率能達到100 GS/s量級[6],并且吞吐率需求以指數級速度增長,大概每5年增長10倍[7].

數十年來發展出數字信號處理器(digital signal processor,DSP)、現場可編程門陣列(field programmable gate array,FPGA)和專用集成電路(application specific integrated circuit,ASIC)等多種數字信號處理平臺.DSP具有強大的運算能力和良好的可編程性,在滿足性能需求的條件下,DSP是構建數字信號處理系統的首選器件.但受到指令串行執行和處理器尋址模式的限制,傳統DSP的FFT運算能力低于FPGA和ASIC實現[8].

“通用核心＋加速器”的結構在獲得通用處理器可編程性和靈活性的同時又能提升特定應用的性能與功耗效率,是未來處理器發展的重要方向.為了提高DSP的FFT處理能力,在DSP中集成FFT加速器成為必然選擇,已有大量理論研究[9]和實際產品[10]出現.現有研究成果存在2點不足:1)與DSP核心相比,FFT加速器的峰值性能沒有體現出明顯優勢;2)對于超長點數FFT的支持能力有限.

本文針對集成于DSP的FFT加速器開展研究工作.注意到將FFT的2維分解算法推廣到多維后,可以將每一維的點數控制在16個點以內,從而能用固定的小點數FFT實現幾乎任意長度的FFT,本文在此基礎上提出面向超長點數FFT的多維分解算法.針對FFT多維分解算法中的轉置和鉸鏈因子生成這2種核心運算開展研究,提出了素數體片上3維轉置存儲器結構解決訪存帶寬利用率低的問題,提出了鉸鏈因子遞推生成算法解決坐標旋轉數字計算機(coordinate rotational digital computer,CORDIC)算法迭代計算周期長的問題.最后,對每一維處理中的小點數FFT進行了精細化電路設計.本文設計的FFT加速器能夠實現最長4G點數的單精度浮點FFT計算,運行頻率能夠達到1 GHz以上,性能達到640 Gflop/s.在點數和性能方面都較已有研究成果取得大幅提升.

1 相關研究

經過數十年的研究,FFT算法發展了許多種類.根據運算形式的不同可以將FFT分為時間抽選(decimation in time,DIT)和頻率抽選(decimation in frequency,DIF).根據基本蝶形運算單元的粒度則可以將FFT分為基2、基4、基8、基16、多基和素數基等.與此同時,大量的流水化和并行化FFT實現結構也被提出,例如陣列并行結構、單路延時置換(single-path delay commutator,SDC)結構、單路延時反饋(single-path delay feedback,SDF)結構、多路延時置換(multi-path delay commutator,MDC)結構和多通路延時反饋(multi-path delay feedback,MDF)結構等[9].

許多研究針對基本運算單元進行精細化設計.例如,采用基22算法[1],對偶序號使用基2算法,對奇序號使用基4算法,減少運算量;采用不同實現方式的乘法器[11]獲得較小的開銷;以CORDIC算法為基礎,將復數乘法與旋轉因子求值統一到一個迭代運算中[12],減少蝶形運算復雜度;通過運算過程中的動態位寬調整[13],減少資源開銷和功耗;采用二項融合點積(fused dot product,FDP)運算和融合加-減(fused add-subtract,FAS)運算[14],實現高效的浮點復數運算.這些研究在小點數FFT計算中普遍取得明顯的優勢,然而,提升長點數FFT計算效率需要超出基本運算單元的范疇進行考慮.

對于長點數FFT,計算的中間結果無法全部存儲在芯片內部.Winograd傅里葉變換算法[15](Winograd Fourier transform algorithm,WFTA)利用旋轉因子特性對FFT進行分解,使用規模較小的2維FFT模擬實現規模較大的一維FFT,是一種高效且資源占用相對較少的FFT實現方法.在處理器[16-17]和FPGA[4,18]上對長點數FFT的實現普遍采用了這種2維分解算法.

長點數FFT加速器的研究大多在2維分解算法基礎上進行改進.Yang等人[19]采用一種支持基2、基4、基8、基16可重構運算單元,實現FFT運算中蝶形運算單元的靈活配置,達到最佳的能效.Tang等人[20]提出一種基數靈活可配的MDF結構,適用于可變長度多路FFT.Chen等人[21]提出一種基于CORDIC算法的可重構浮點FFT加速器結構,通過旋轉方向預測減少硬件開銷,通過旋轉角度的實時生成節省存儲需求.于東等人[22]在FFT處理器中將緩存劃分成32個體,通過對緩存的靈活調度實現“乒乓”操作,提高長點數FFT的運算性能.雷元武等人[9]設計了一種基于矩陣轉置操作的可變長度FFT加速器結構,提出“乒乓”多體數據存儲器、基于基本塊的快速矩陣轉置算法、結合查表和基于CORDIC算法的混合旋轉因子產生策略等優化方法.在這些研究中,運算量的精簡、旋轉因子高效生成和提高存儲訪問效率始終是關注的重點.

2 算法分析

2.1 FFT算法介紹

N點序列{x0,x1,…,x n}的DFT定義為

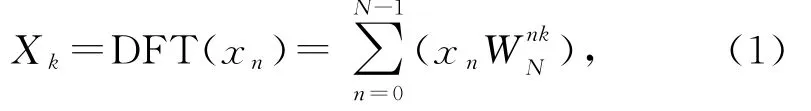
其中,k∈[0,N－1],旋轉因子

Cooley-Tukey算法[2]是目前應用最為廣泛的FFT算法.根據旋轉因子在計算過程中的位置分為DIT和DIF兩類.

以基2 DIT算法為例進行簡要說明[23].當N為偶數時,令x0,n＝x2n,x1,n＝x2n＋1(0≤n≤N/2－1,n為整數).若X0,k＝DFT(x0,n),X1,k＝DFT(x1,n),(0≤k≤N/2－1,k為整數),則:

式(2)表明:若將任何一偶數點序列按n的奇偶性分成2個子序列,則原序列的DFT可由2個子序列DFT的線性組合得到.

按照式(1)直接進行N點DFT計算,需要N2次復數乘法和N(N－1)次復數加法,而采用式(2)的蝶形運算方法則只需(NlbN)/2次復數乘法和NlbN次復數加法.FFT算法極大縮減了DFT的運算量.

2.2 多維分解FFT算法

觀察式(2)可以發現,每一級蝶形運算的輸入數據都是上一級蝶形運算輸出數據混洗的結果.而且,隨著蝶形運算級數的增加,混洗的范圍越來越大.這就導致,當FFT的點數長到無法在加速器內部一次性加載所有輸入數據的時候,將會產生大量的非連續訪存,這與半導體存儲器采用并行總線方式提高帶寬的機制不兼容.對于超長點數FFT運算需要找到訪存連續性較好的算法.

假設N＝L×M,由式(1)得:

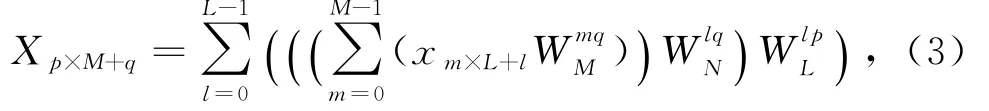
其中,p∈[0,L－1],q∈[0,M－1].

從式(3)可以看出,N點DFT分解為了2維.第1維是獨立的L組M點DFT(其結果需要乘以鉸鏈因子W lqN),第2維是獨立的M組L點DFT.所以,可以將長點數FFT轉化為小點數FFT的2維分解[4]:1)將N點的數據分解為L行M列的矩陣;2)對所有行分別做M點的FFT;3)將所有元素與各自的鉸鏈因子相乘;4)進行矩陣轉置,得到M行L列的矩陣;5)對所有行分別做L點的FFT;6)再次進行矩陣轉置,得到結果.

將上述2維分解進一步推廣.假設N＝B d,由式(3)得:

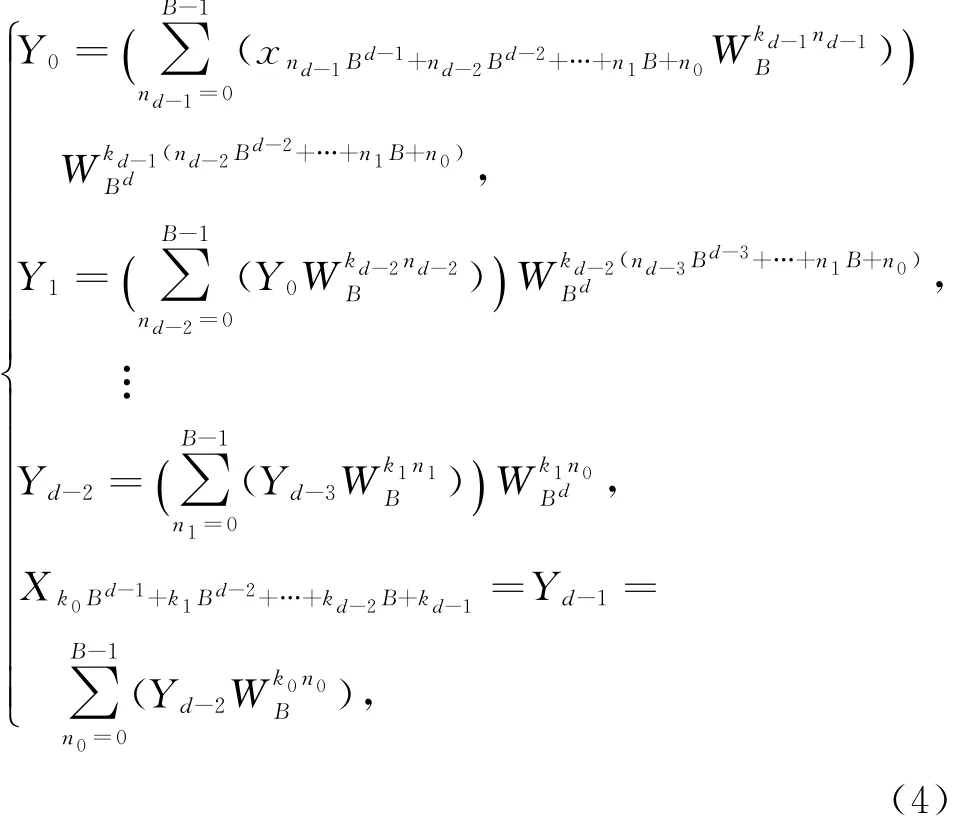
其中,n0,n1,…,n d－1∈[0,B－1];k0,k1,…,k d－1∈[0,B－1].根據式(4)可以得到基礎FFT點數為B的d維分解算法.

算法1.FFT的多維分解算法.

FFT_MD(d;x0,x1,…,x B d－1):/?遞歸定義,B點FFT作為基本運算,參數d為維度?/

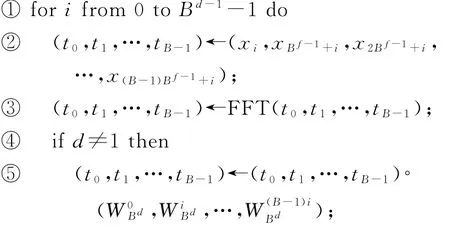
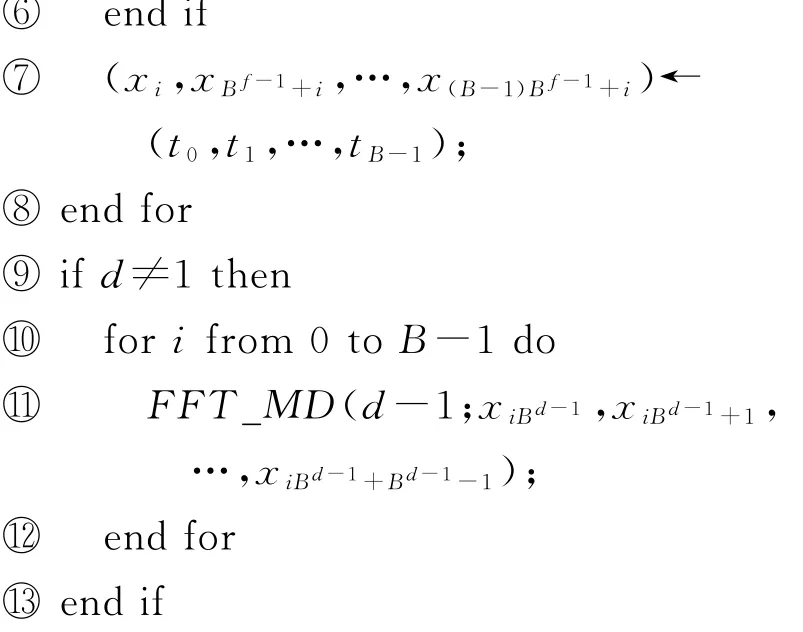
算法1總共進行d輪,每輪完成B d－1組B點FFT.每個元素讀、寫各d次,參與B點FFT運算d次,乘鉸鏈因子d－1次.

如果存儲器的訪問粒度為B個點,則算法1中的訪存將是“按維連續”的.最基本的運算單元就是B點FFT,每次運算都是在相應的維上連續的B個數據參與運算.采用第3節中將要介紹的3維轉置存儲器則可以將“按維連續”的訪存轉換為連續訪存,從而解決了超長點數FFT運算的訪存連續性問題.

另外,在算法1中計算順序是按照第d維到第1維進行的,計算第i維(1≤i≤d)的B d－1個B點FFT的過程是相互獨立的.當其他維坐標固定時,第i維和第i－1維構成一個B×B的矩陣.如果以這樣的矩陣為基本處理單元,則2維處理可以合并,讀、寫B d－2次B2個元素可以進行B d－2×2B次B點FFT運算.運算次數不變的情況下,讀、寫次數還能減半.

3 設計實現

考慮到超長點數FFT的精度要求,本文選擇單精度浮點作為基本數據表示.在此基礎上,選擇16點FFT作為基本運算.

3.1 數據流處理

從根本上說,FFT計算過程中需要以2的冪為步長交叉訪問數據,這與存儲器的連續訪問機制不匹配,導致存儲帶寬利用率低,計算性能無法充分發揮.3維轉置運算搭建了連續訪問數據與跨步交叉訪問數據之間的橋梁.在此基礎上,通過2維轉置實現算法1中2維處理的合并,進一步減少訪存量.

3.1.1 3維轉置運算

假設存儲器的訪問粒度為B個點,則意味著FFT加速器每次必須按第1維的B個點進行讀、寫.為了存儲一個第i維和第i－1維構成的B×B矩陣,需要具備存儲B3個點的能力.因為,讀入B3個點才能同時得到B個完整的第i維和第i－1維構成的B×B矩陣.此時,如果能夠按照第i維或第i－1維同時將B個數據取出,則實現了無帶寬損失的3維轉置運算.

存儲器的訪問粒度按照16個點設計,具備存儲163＝4 096個點的能力,容量為32 KB,使用靜態隨機訪問存儲器(static random access memory,SRAM)實現.SRAM無法進行任意方向的讀寫,即便采用2維SRAM陣列[24](每個存儲單元變成了2個端口,增大了SRAM的面積)仍然難以實現3維轉置運算.因此,本文采用基于SRAM的無沖突體編址技術實現3維轉置運算.

根據高慶獅等人[25]對素數存儲系統的研究,對于跨步為2的冪的訪問,采用素數個存儲體,即可消除存儲體訪問沖突.假設訪問地址為a,a＋2r,a＋2×2r,…,a＋15×2r,采用17個存儲體.令2rmod 17＝t,則各地址所在的體為amod 17,(a＋t)mod 17,(a＋2t)mod 17,…,(a＋15t)mod 17.如果第i個地址和第j個地址落在同一個體,即(a＋it)mod 17＝(a＋jt)mod 17,則(i－j)tmod 17＝0,只有i＝j等式才能成立.

3維轉置運算的存儲體可以存儲一個多維張量中按照某3維截取的一個立方體.由于采用17個體在跨步為2的冪訪問時不存在體沖突,可以并行讀入該立方體,并且對任意2維并行轉置讀出.作為轉置用存儲器,每個體需要存儲個點,即每個體寬度為64 b(8 B)、深度為241.

按照3維編址進行分析.初始狀態下,第1組寫入地址為(0,0,0)～(0,0,15),第2組寫入地址為(0,1,0)～(0,1,15),依次類推,當寫入地址為(15,15,0)～(15,15,15)時,完成全部4 096個點的寫入.在完成地址(15,0,0)～(15,0,15)的寫入后,即可讀出轉置后的第1組地址(0,0,0)～(15,0,0).所以,當4 096個點完全寫入時,已讀出多組數據,下一批4 096個點可以流水寫入.

新的4 096個點第1組寫入地址為(0,0,0)～(15,0,0),第2組寫入地址為(0,1,0)～(15,1,0),依次類推,當寫入地址為(0,15,15)～(15,15,15)時,完成全部4 096個點的寫入.在完成地址(0,0,15)～(15,0,15)的寫入后,即可讀出轉置后的第1組地址(0,0,0)～(0,0,15).

根據讀/寫的維序即可計算讀/寫操作下一拍的3維編址(z,y,x).

根據3維編址得到體地址與體內地址為

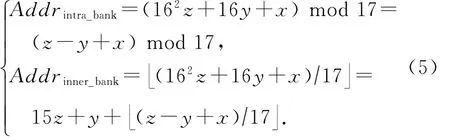
并不需要對所有地址進行計算,每次讀/寫的16個地址,只需要先計算出第1個所在的體地址和體內地址,其余15個可以快速得到.另外,對于以2的冪加1為除數的除法和模運算存在快速硬件實現方法[25].

從式(5)所顯示的體地址規律可以看出,第1維和第3維都是連續循環遞增的,第2維是連續循環遞減的.無論是輸入數據還是輸出數據,可以根據地址計算出移位位數.分別對輸入/輸出的16個數據進行順序和逆序排列之后移位,移位采用2級對數移位器.總體結構如圖1所示:

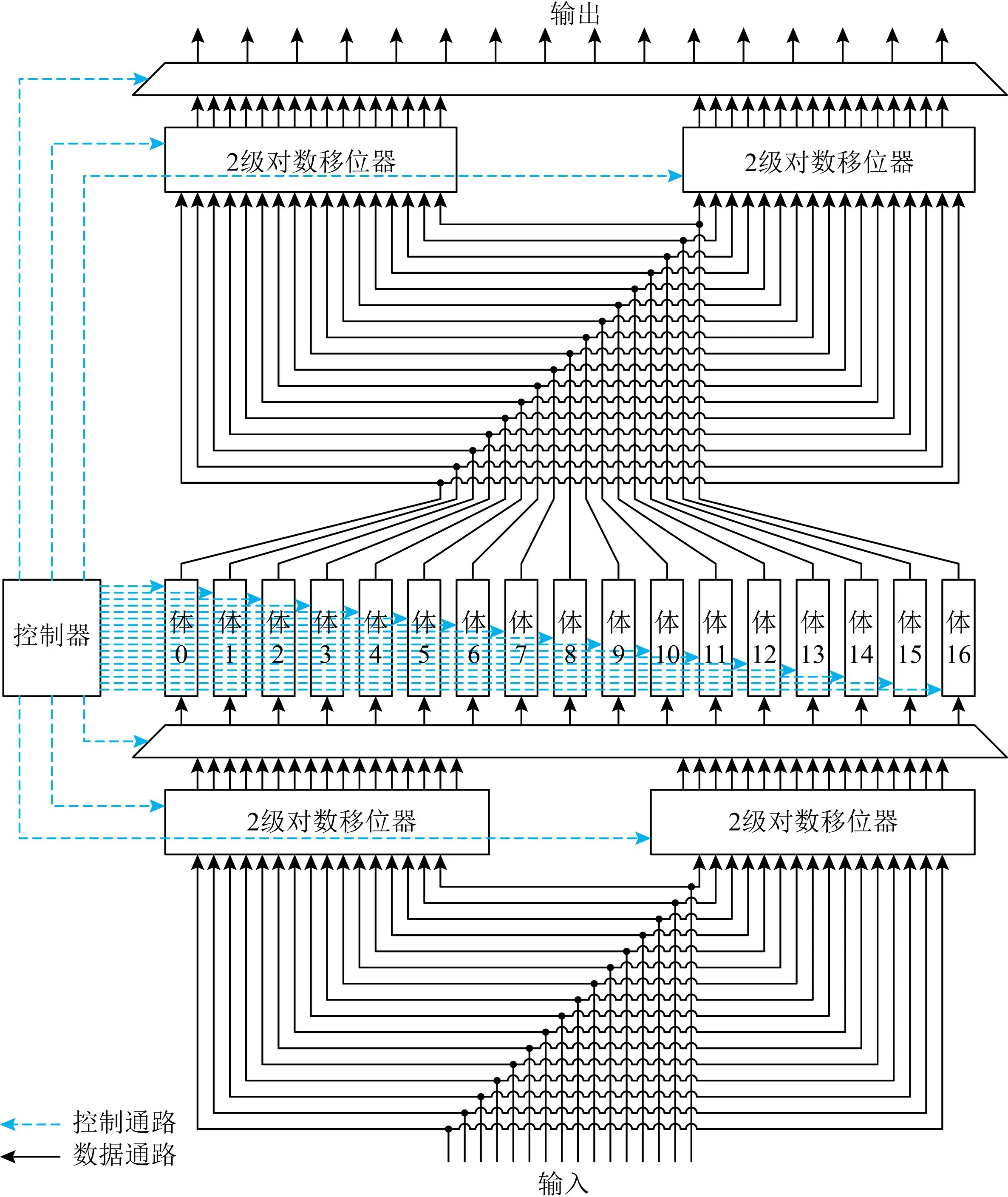
Fig.1 Structure of 3-dimensional transposition operation module圖1 3維轉置運算模塊結構

3.1.2 2維轉置運算

2維轉置運算采用行向輸入、列向輸出的存儲器陣列實現.需要存儲162＝256個點,存儲容量為2 KB.芯片中容量較小的存儲器陣列可以采用觸發器、SRAM或鎖存器實現.SRAM的面積和功耗開銷最小,但是由于2維轉置運算對存儲器有特殊要求,需要按行寫入、按列讀出,標準SRAM不支持該功能,因此需要采用定制設計[24],開發周期長且不利于擴展.觸發器的面積和功耗開銷最大.因此,選擇鎖存器作為基本存儲單元.2維轉置運算的存儲器如圖2所示.

通過2個這樣的鎖存器陣列來實現轉置處理的流水化,如圖3所示.讀選擇信號和寫選擇信號互為反相,根據讀、寫次數來進行判斷.

3.2 鉸鏈因子處理

對FFT運算點數的支持并不需要無限大,超出主存容量是沒有意義的.加速器按照最大支持4G點FFT設計,則存儲容量需要32 GB,基本達到當前內存容量的極限.更長點數FFT則依賴于軟件方法實現.

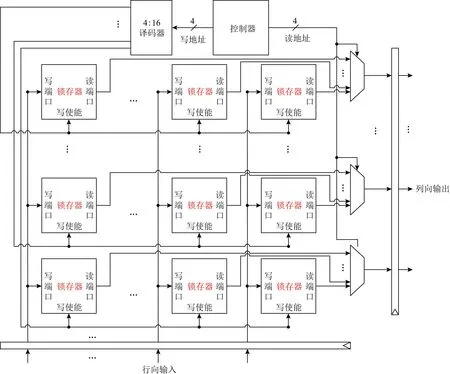
Fig.2 Memory for two-dimensional transposition operation圖2 2維轉置運算的存儲器

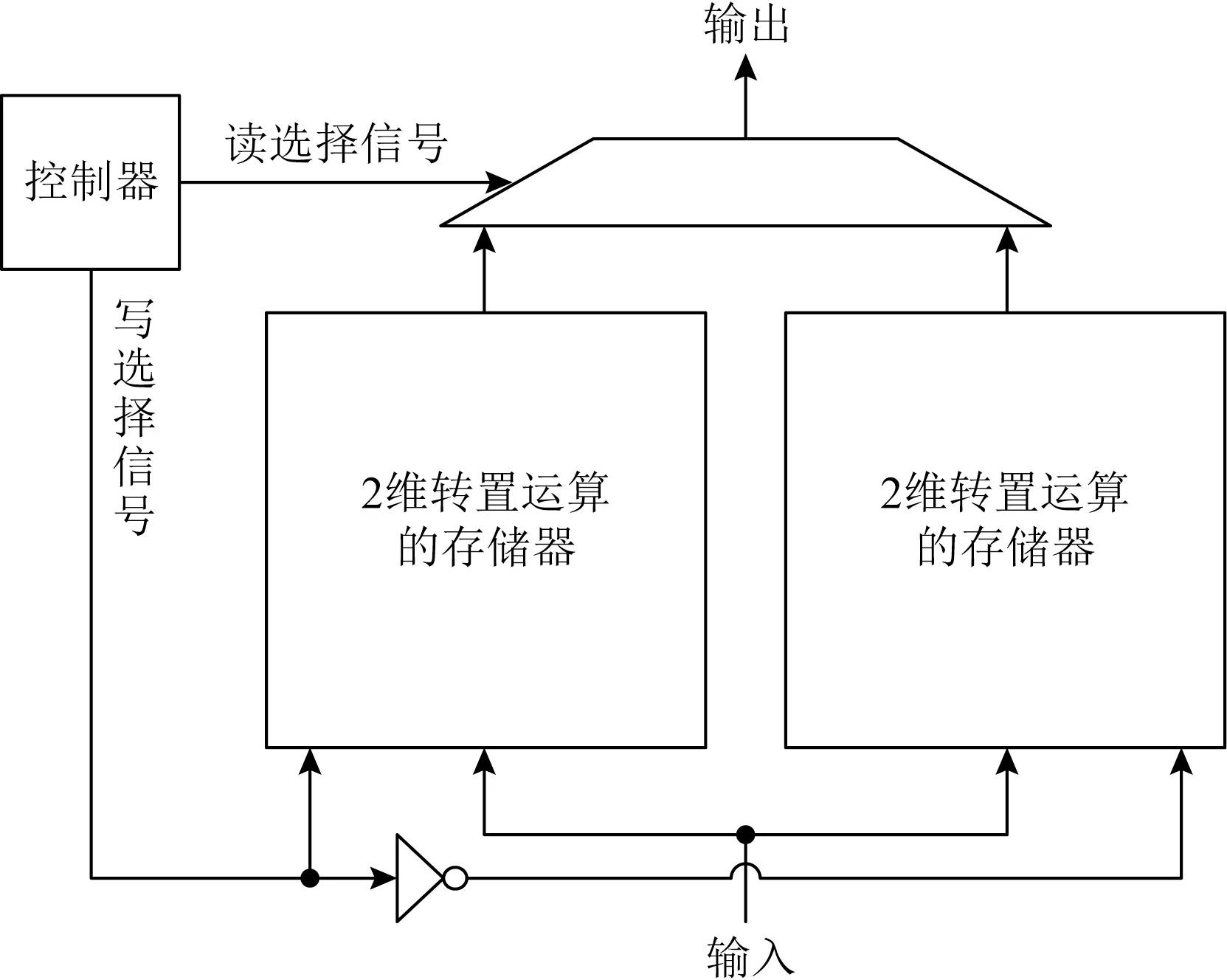
Fig.3 Structure of 2-dimensional transposition operation module圖3 2維轉置運算模塊結構

在許多研究中采用CORDIC算法生成鉸鏈因子,需要進行十幾個甚至幾十個時鐘周期的流水化迭代處理.CORDIC算法可以生成任意角度的坐標值,對于有限集合而言則過于強大.我們注意到,即便對于4G點FFT,也只需要根據算法1進行8維分解,鉸鏈因子是一個有限集合,而且每一組鉸鏈因子與前一組鉸鏈因子存在遞推關系,因此,可以使用較為簡便的方法實現鉸鏈因子生成.

假設數據組織為8維維序結構,以處理第4維鉸鏈因子為例.x n7,n6,n5,n4,n3,n2,n1,n0需要的鉸鏈因子為.由于同時處理n3＝0～15,需要同時生成.在算法1中,處理的第1組點為鉸鏈因子均為處理的第2組點為鉸鏈因子分別為…;處理的第16組點為鉸鏈因子分別為;處理的第17組點為,鉸鏈因子分別為,依次類推.對于同時處理的16個鉸鏈因子中的第k個,可以采用算法2遞推生成.

算法2.鉸鏈因子生成算法.

輸入:上一個鉸鏈因子Wpre、上一個計數值Cpre、鉸鏈因子的維度d;

輸出:鉸鏈因子W、計數值C.

初始狀態W＝1,C＝0;

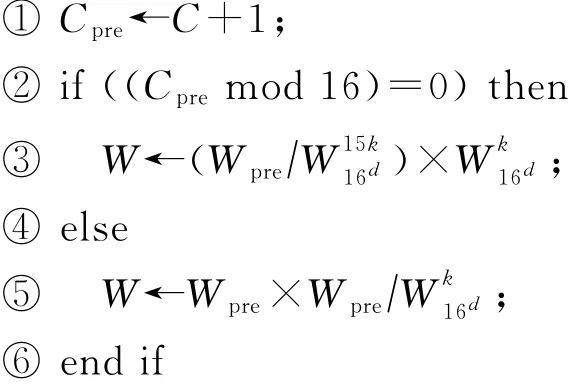
為了并行執行,鉸鏈因子處理需要16個鉸鏈因子生成模塊和16個單精度浮點復數乘法器.維度控制邏輯根據FFT命令解析出當前運算的維度,發送給每個鉸鏈因子生成模塊.

鉸鏈因子生成模塊結構如圖4所示.控制邏輯根據處理的維度和計數值生成選擇信號.寄存器0用于存儲當前的鉸鏈因子,寄存器1用于存儲上一個計數值整除16時的鉸鏈因子.控制邏輯根據算法2實現.基礎旋轉因子包括W k16,W k162,…,W k168為常數,接入固定電平即可.

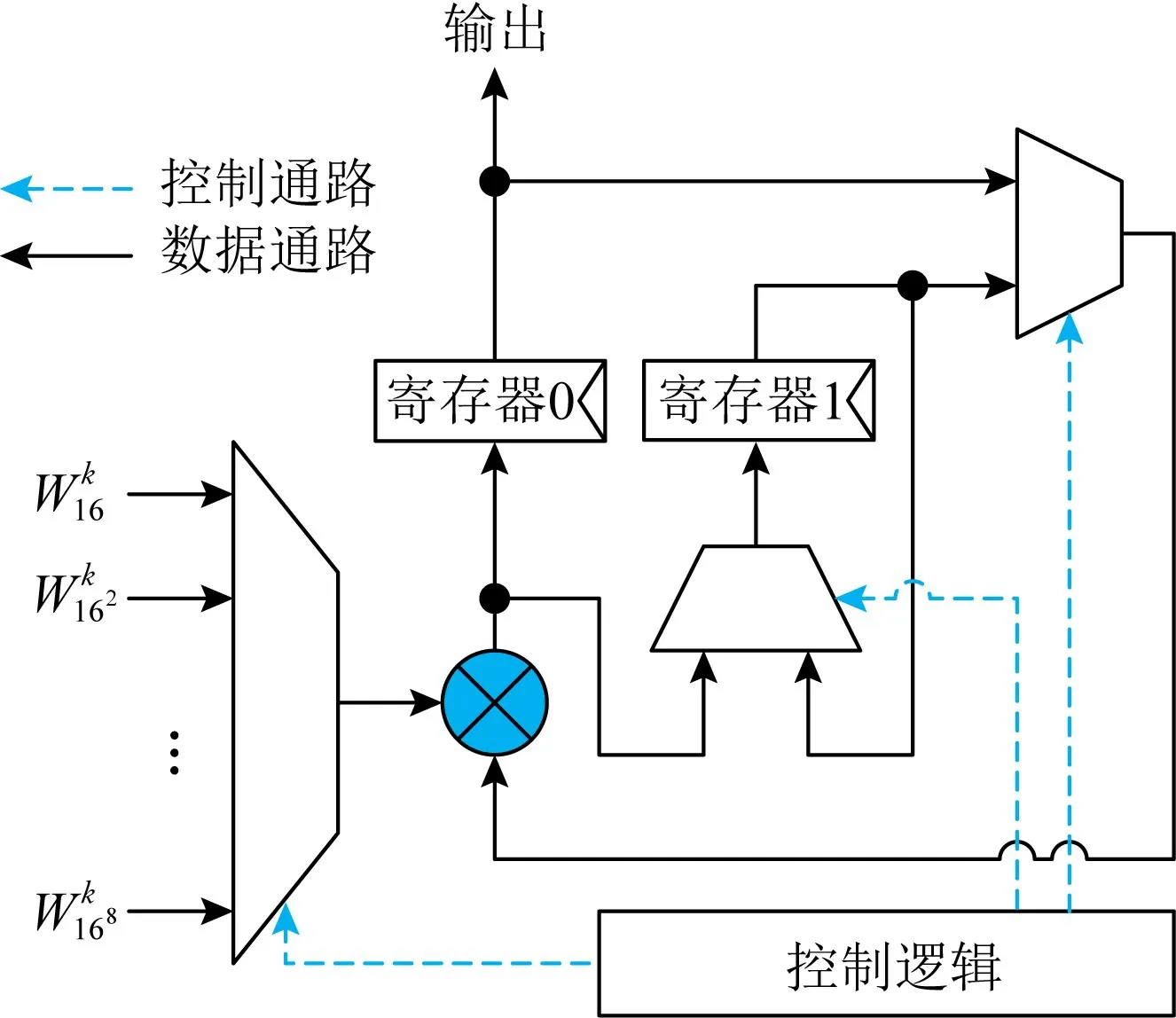
Fig.4 Twiddle factor generation module圖4 鉸鏈因子生成模塊

從算法2和圖4可以看出,鉸鏈因子生成的延遲與乘法運算的延遲相同,較傳統的CORDIC算法有明顯優勢.但是,該方法也帶來了單精度浮點復數乘法器的額外開銷.

3.3 基本運算

本文采用IEEE 754-2008標準[26]單精度浮點作為基本數據表示.以Swartzlander等人[14]提出的FDP運算和FAS運算作為基本的浮點運算來構造單精度浮點復數運算.對于復數a＝aRe＋iaIm和b＝bRe＋ibIm,其乘積c＝cRe＋icIm＝a×b＝(aRe＋iaIm)×(bRe＋ibIm)＝(aRebRe－aImbIm)＋i(aRebIm＋aImbRe).FDP實現4個單精度浮點數a0,a1,a2,a3的a0a1＋a2a3運算或a0a1－a2a3運算.2個FDP(分別配置為加和減)則恰好能夠實現一個復數乘法.FAS運算同時完成蝶形運算中的加法和減法運算.

16點FFT運算采用基4 DIT算法實現,總體結構如圖5所示,包括3個混洗單元、8個4點蝶形運算單元和8個旋轉因子乘法單元.

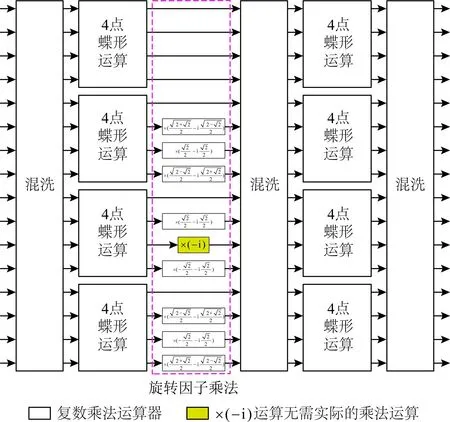
Fig.5 Sixteen-point FFT operation module圖5 16點FFT運算模塊

混洗單元內部只有連線,實現地址反序輸出,如圖6所示:

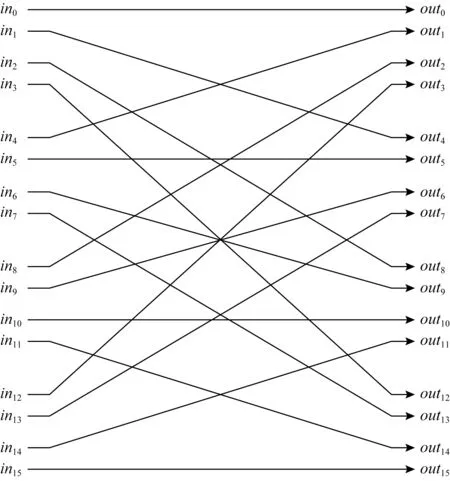
Fig.6 Shuffle unit圖6 混洗單元

4點蝶形運算單元完成的運算為

采用圖7所示結構實現,其中,Re和Im分別表示一個復數的實部和虛部.

Fig.7 Four-point butterfly unit圖7 4點蝶形運算單元

3.4 控制結構

FFT加速器總體結構如圖8所示,包括命令隊列、讀/寫控制器、讀/寫緩沖、3維轉置存儲器、16點FFT運算模塊、鉸鏈因子處理模塊和2維轉置存儲器等.

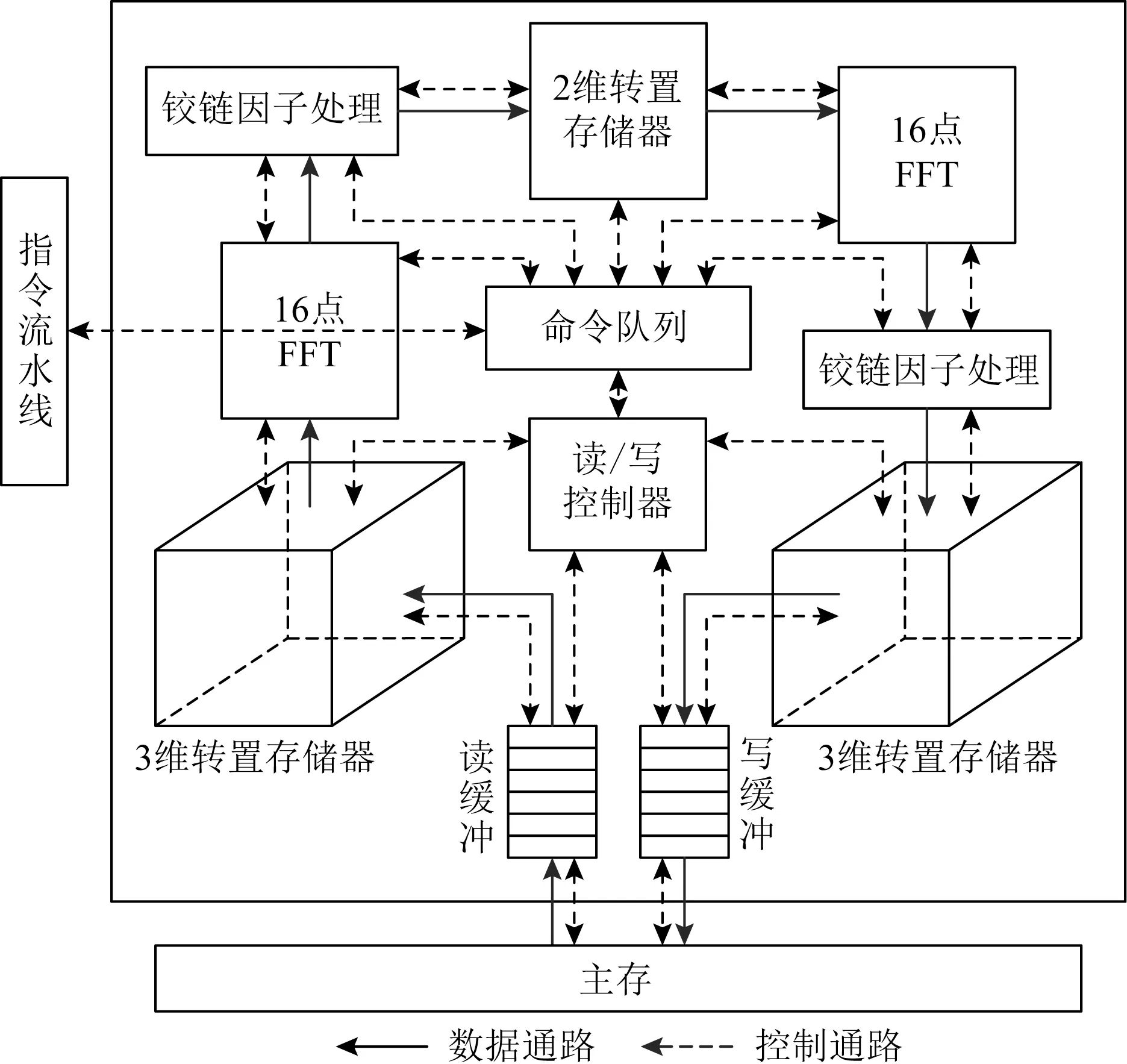
Fig.8 Overall structure of FFT accelerator圖8 FFT加速器總體結構

命令隊列從DSP核心的指令流水線接收命令并進行解析,生成各模塊控制信號.讀/寫控制器根據命令隊列解析的地址對讀/寫緩沖和3維轉置存儲器進行控制.讀/寫緩沖與存儲器交互,用于讀/寫數據的平滑.

FFT加速器的執行方式為:1)DSP核心通過寫特殊存儲空間或特殊寄存器方式對FFT加速器進行配置,包括原始數據地址、計算結果地址、計算規模等;2)DSP核心發出異步FFT指令;3)FFT加速器從存儲器中讀取數據進行FFT計算,并將計算結果寫入指定存儲器地址中;4)通過中斷或回答字機制返回FFT完成信號給DSP核心.

整個FFT加速器通過命令隊列和讀/寫控制器進行管理,工作流程為:1)DSP核心的指令流水線向命令隊列發出FFT指令;2)命令隊列對FFT指令進行解析,解析出讀/寫命令;3)讀/寫控制器生成讀/寫地址,發送給讀/寫緩沖;4)讀緩沖從存儲器中讀數據;5)讀緩沖將數據發送給輸入3維轉置存儲器;6)輸入3維轉置存儲器根據維序將轉置后數據發送給16點FFT運算模塊;7)FFT計算后結果經過鉸鏈因子處理,送入2維轉置存儲器;8)2維轉置存儲器輸出送入另一個16點FFT運算模塊;9)FFT計算后結果經過鉸鏈因子處理,送入輸出3維轉置存儲器;10)輸出3維轉置存儲器根據維序將轉置后數據發送給寫緩沖;11)寫緩沖根據寫地址將數據寫回存儲器.

4 實驗與分析

4.1 綜合結果

本文使用Verilog語言對FFT加速器進行了完整實現.其中,單精度浮點FDP和FAS都采用4級流水線設計.

使用物理信息相關的DCG綜合流程[27],對各模塊和整個FFT加速器采用TT Corner工藝進行綜合,關鍵路徑延時為954 ps(運行頻率能夠達到1 GHz以上),面積為462 100μm2,功耗為1 210 m W.FFT總體及各模塊綜合結果如表1所示.

表1中同時列出了一個4級流水的單精度浮點融合乘加(fused multiply-add,FMA)部件的綜合結果作為對比.可以看出,整個FFT加速器的面積大致相當于500個單精度浮點FMA部件.本文提出的加速器結構中,4點蝶形運算含有8個FAS,16點FFT運算含有8個4點蝶形運算和8個旋轉因子乘法,鉸鏈因子處理中含有32個復數乘法器.可以看出,各子部件單獨綜合結果與總體綜合結果基本吻合.3維轉置存儲器中使用的每個SRAM存儲器的面積為2 500μm2,SRAM的總面積為34×2 500μm2＝85 000μm2,占整個FFT加速器的18.39%.

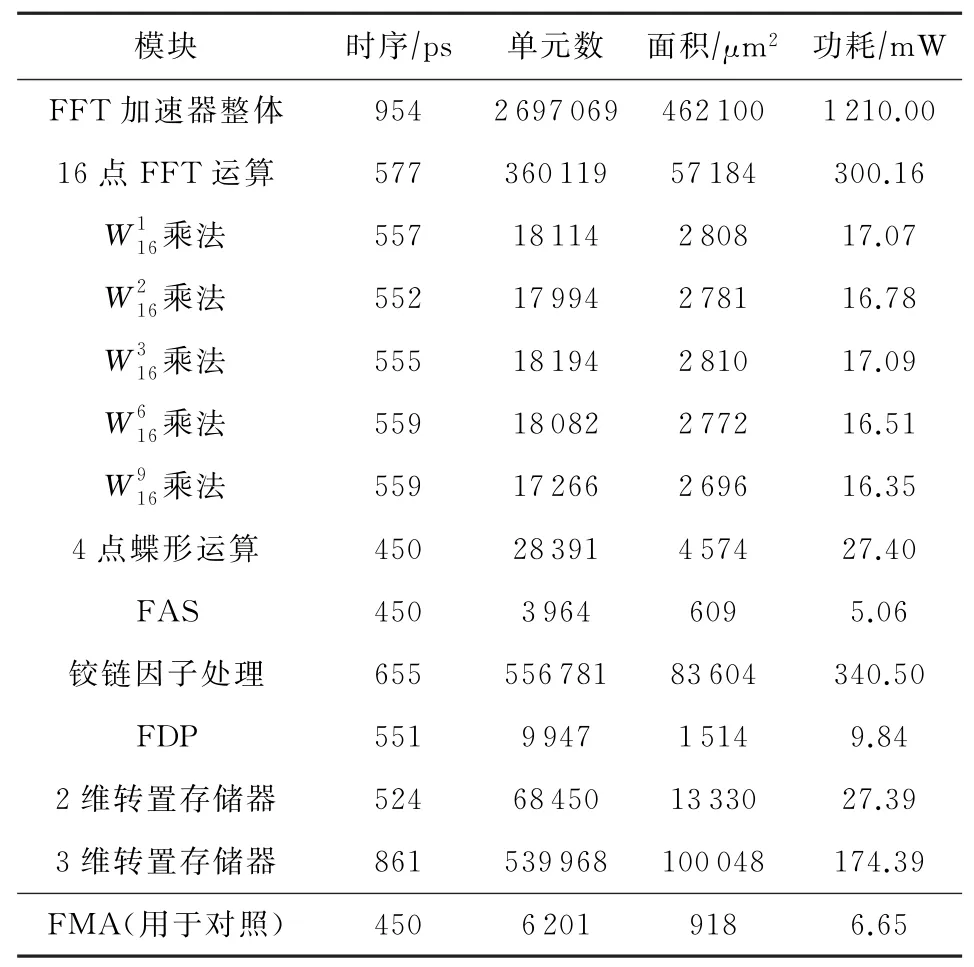
Table 1 Synthesis Result表1 綜合結果

本文還對FFT加速器進行了FPGA實現,其中,器件型號為XCVU440-FLGA2892.時鐘頻率可以達到136.6 MHz,資源消耗情況如表2所示,占用了177 875個REG、657 790個LUT和34個Block RAM.從綜合結果來看,本文設計的FFT加速器具有較強的可實現性.

Table 2 FPGA Resources Consumption of Realization表2 FPGA實現資源消耗

4.2 比較與分析

4.2.1 性能與開銷

以基2 DIT算法作為性能計算的標準,一個蝶形運算及其完成的基本操作需要4個乘法操作和6個加/減法操作,共10個操作[9].對于N點FFT,總共需要0.5NlbN個蝶形運算,所以總的計算量為5NlbN個操作.

根據綜合結果,本文設計的FFT加速器可以運行在1 GHz,內部包含2個16點FFT運算模塊,性能能夠達到2×5×16×(lb16)flop×1 GHz＝640 Gflop/s.

Table 3 Performance Comparison of FFT Accelerator表3 FFT加速器性能與開銷對比

表3中對比了若干種長點數FFT加速器的性能和開銷.可以看出,采用綜合實現方式,本文提出的FFT加速器與現有研究中的浮點FFT加速器相比,能夠取得1～2個數量級的性能提升.在與現有研究中的定點FFT加速器比較時,性能上也有優勢.得益于多維分解算法的使用,本文將單維處理點數固定為16,從而可以高密度集成16點FFT運算部件.同樣得益于多維分解算法的使用,本文設計的FFT加速器能夠支持到4G個點,遠遠超過其他實現方法.

由于不同研究者采用的工藝或FPGA型號不同,難以給出一個統一的開銷標準.我們既給出了綜合結果,也給出了FPGA實現結果,便于進行開銷對比.與其他綜合實現的研究相比,本文設計的FFT加速器的面積和功耗開銷較高,但是性能面積比和性能功耗比都具有優勢.

4.2.2 存儲帶寬

假設FFT加速器的計算性能為Pcom,基本處理點數為M(對于本文設計的FFT加速器Pcom＝640Gflop/s,M＝162＝256).對于N點FFT(N＞M,存儲器中能夠容納N個點數據),計算量Acom＝5NlbNflop,訪存量Amem＝16N(lbN/lbM)B.存儲器帶寬Bmem需滿足:

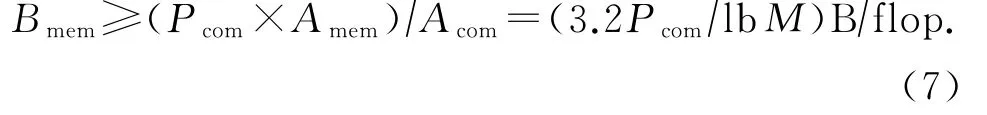
所以,本文設計的FFT加速器,需要的存儲器帶寬為0.4×640 GB/s＝256 GB/s.對于使用DDR存儲器的高端處理器,這個帶寬是可以滿足的.對于使用GDDR和HBM存儲器的處理器,存儲帶寬更高.

對于主存帶寬受限的情況(以128 GB/s為例),則可以通過設置緩存的方式來達到對計算能力的支持.緩存的帶寬需要滿足256 GB/s(對于片上SRAM是容易實現的),緩存能夠容納的點數M?可以視作主存視角的基本處理點數.則lbM?≥(3.2×640)/128＝16,M?≥216,即緩存容量需要達到512 KB,對于處理器而言也是容易實現的.

對于主存帶寬較低的情況(以32 GB/s為例,假設片上緩存容量為2 MB),點數小于256 K時能夠達到峰值計算性能,點數大于256 K時的計算性能

4.2.3 計算效率

本文設計的FFT加速器以256點為基本處理單位,當計算的總點數為256的冪時,性能可以得到充分發揮,其他情況下計算效率難以達到100%.

對256點到4G點FFT的計算效率進行模擬測試,結果如圖9所示.可以看出,對于點數不是256冪的情況,點數較小時計算效率降幅較大,而點數較大時計算效率降幅則較小.這是由于,當點數較大時,在大部分情況下都能選擇出完整的2個維度進行FFT計算.

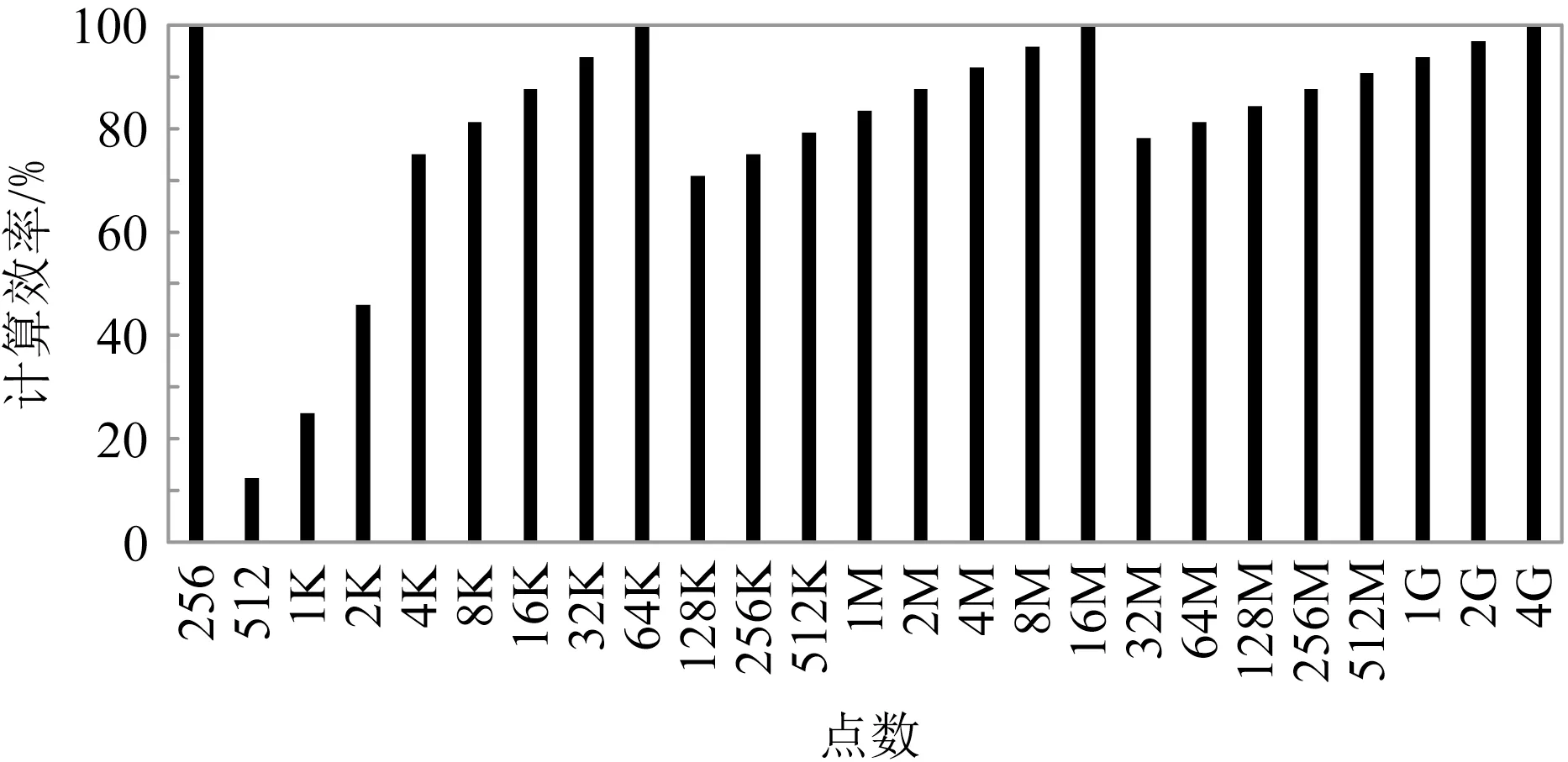
Fig.9 Computing efficiency of FFT accelerator圖9 FFT加速器的計算效率

在本文設計的FFT加速器中提高小點數FFT的計算效率仍然需要進一步探索.

5 總 結

本文提出一種可集成于DSP的高性能超長點數FFT加速器結構.通過基于素數體的片上3維轉置存儲器、高效鉸鏈因子生成技術和精細化FFT運算電路設計,實現了超長點數FFT的多維分解算法.對于4G以內點數的單精度浮點FFT計算,能夠達到640 Gflop/s的性能,大幅提升了FFT加速器的性能和支持的點數.