FHN神經元小世界網絡隨機共振下的弱信號增強?

房 濤范影樂蔡哲飛武 薇

(杭州電子科技大學模式識別與圖像處理實驗室,浙江 杭州310018)

20世紀80年代Benzi等人在研究周期性復發的冰河期問題,發現在偏心率如此小的周期性下,地球的氣候不足以發生這么大的變化,為了合理的解釋這種現象,他們提出了雙穩態的非線性氣候模型,完美的解釋了周期性冰河期的原因,并將這種現象稱之為隨機共振[1－2]。自此之后,隨機共振吸引了大批學者的研究關注,同時為噪聲與弱信號的處理提供了一種新的思路[3]。

隨后,越來越多的學者在生物信號處理過程中也發現了越來越多隨機共振的現象,例如密蘇里大學的研究團隊發現在水鰲蝦尾扇感知細胞感知過程中隨機共振效應[4]；Levin等在研究蟋蟀觸須的感知細胞中,發現了外界合適的噪聲干擾有助于提高蟋蟀對微弱信號刺激的響應[5]；Braun等則在實驗的過程中,發現合適的噪聲有利于鯊魚神經細胞膜振蕩信號的傳播[6－7]；Stemmber等發現動物腦皮質的視覺神經對于方向感知的過程中,也存在隨機共振現象[8]；Liljenstr?m等利用計算機模擬了海馬神經網絡模型,發現了隨機共振的類似現象[9]；另外,在2003年Mori等人首次在人腦視覺處理區域觀察到了隨機共振現象[10]。隨著對這些隨機共振現象不斷深入的研究,一些研究者開始嘗試應用隨機共振現象解決一些實際問題,比如Moss等將隨機共振技術運用于模糊圖像信號的增強[11]；Morse等則運用隨機共振現象提高助聽器對輸出共振峰頻率的檢測能力[12]。另外,一些研究人員們陸續也在諸如Hodgkin-Huxle(HH)神經元模型、FitzHugu-Nagumo(FHN)神經元模型、Integrate-Fire(IF)神經元模型以及離散的Rulkov神經元模型中也都觀察到了隨機共振現象[13－15]。關于這些在生物系統中已經取得的研究成果和潛在的應用,說明隨機共振可能是神經信息感知、傳遞和處理過程的普遍現象和重要機制[16－17]。但這些過程多是基于真實生物系統的生理現象觀察,或者出于簡化模型計算的考慮,大多是基于單神經元非線性系統的模型建模,并沒有考慮到生物神經元系統集群所帶來的更加強大的表征能力、非線性擬合特性以及系統穩定性的作用,因此神經元網絡中的隨機共振現象并沒有得到深入研究,在處理噪聲與弱信號的強魯棒性也沒有得到深入的分析。

近些年來,復雜網絡已經成為計算神經的研究熱點之一,涉及物理學、生物學以及計算機科學等多個學科領域[18－19]；另外,復雜網絡的模型也得到了豐富,例如陸續提出的規則網絡模型、隨機網絡模型、小世界網絡模型以及無標度網絡模型等[20],尤其是越來越多的生理實驗研究表明,生物神經元系統具有小世界網絡特性[21]。因此,本文提出了一種小世界神經元網絡構建思路,并嘗試應用于弱信號增強。首先基于概率隨機重連的方法構建小世界神經元網絡,將改進后具有隨機共振的非線性FHN神經元設置為網絡節點,同時基于生物神經元間的信息傳遞特性,設計網絡中互連神經元節點之間基于動態突觸的信息流傳遞方法,最后根據對輸入信號和輸出信號互相關系數的實時計算,舍棄互相關系數過低的異常輸出節點值,提出了小世界網絡有效神經元節點的輸出信號均值融合方法,可以有效提高網絡系統隨機共振的魯棒性,避免網絡系統中單個神經元的異常輸出,降低了弱信號的復原誤差,最后通過對周期弱信號和非周期弱信號的實驗證實了本方案的可行性。

1 基本原理

動物腦皮質的視覺神經生理實驗發現隨機共振可以有效地增強視覺信息,并能強化生物的視覺感知能力；隨后在以HH模型以及FHN模型等簡化模型為代表的神經元動力學模型上開展了較多的神經計算仿真研究[22]。因此在單個神經元意義上的隨機共振已經得到深入廣泛的研究,其研究成果已經應用在眾多領域,比如圖像增強、故障信號檢測等等。但必須要指出的是,為有效提高系統的魯棒性,神經元在大腦中往往是以集群形式工作[23]。

因此,本文從生物神經生理機制的角度出發,提出了基于概率隨機重連的小世界神經網絡構建方法,以FHN神經元模型作為網絡節點,但改變了FHN神經元慢特征和膜電位特征時間參數保持一致的傳統思路,從而可以靈活地改變膜電位勢函數勢壘以提高勢阱間的躍遷概率；同時考慮到網絡中神經元節點之間具有受時空調制的動態突觸連接關系,因此本文提出基于距離連接權重的動態突觸神經元節點信息流傳遞方法；最后為了有效而且準確地利用網絡節點輸出信息,通過實時計算輸入信號和輸出信號的互相關系數,舍棄互相關系數異常的節點輸出信息,提出了一種網絡節點均值融合策略對神經元節點輸出信息融合。在合適的輸入信號和噪聲信號下,可以達到輸入信號、噪聲與FHN神經元節點的隨機共振實現弱信號的增強復原,并通過調節網絡中FHN神經元節點的內部噪聲實現神經元群的同步放電,避免了單個神經元節點信息的輸出不確定性,實現對含噪聲弱信號的有效增強復原,具體的系統原理結構如圖1所示。

1.1 FHN神經元隨機共振特性

FHN神經元是在Hodgkin-Huxley模型的基礎上簡化得到的,盡管非常簡潔,但卻反映了神經元的本質特征,通過非線性正反饋膜電位描述“再生自激”現象,非線性反饋門電壓描述恢復過程,可以模擬神經元的大多數特性。Longtin等利用FHN神經元模型對小龍蝦神經系統的隨機共振現象進行了研究,并取得了較好的實驗結果。其具體形式如式(1)所示:

圖1 系統結構圖

式中:v表示快變量即神經元的膜電位,ω表示恢復變量,b表示無量綱的正數；εv、εω分別表示膜電位和恢復變量的特征時間,傳統模型為了簡化計算過程,通常假設上述兩個特征時間為同一數值。為了更加靈活地改變膜電位勢函數勢壘以提高勢阱間的躍遷概率,本文對膜電位和恢復變量的特征時間進行獨立設置,從而在相同的模型結構情況下,獲得更為豐富的動力學行為。

圖2 FHN神經元v－ω相圖

如圖2所示,本文通過對FHN神經元v－ω相位圖以及膜電位勢函數的動力學特性分析,發現FHN神經元的相圖主要涉及三個區域分別是震蕩區域、雙穩態區域和興奮區域。在震蕩區域內,狀態點將隨著極限環移動；在興奮區域內,神經元出現了脈沖發放；雙穩態區域內,狀態點將會緩慢地回到某個穩定的穩定點。根據v－ω相位圖可以發現,初始時刻狀態點開始迅速地移動到立方零斜線的右側分支,然后沿著右側分支向上達到立方零斜線的局部最大值,完成一次動作電位的發放；接著狀態點沿著立方零斜線上側轉化到左側分支,系統的動力學是不穩定的,處于絕對不應期,在任何刺激下都無法產生動作電位；最后,狀態點回到穩定點,在這段時間里處于相對不應期。通過根據式(2)定義勢函數V,即

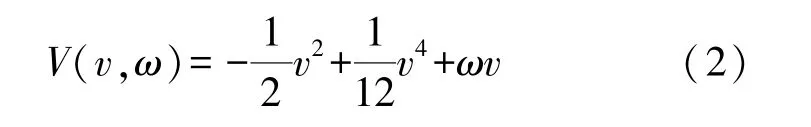
由于εv≤εω,ω在式(2)中的時間尺度下可以視為一個常量,在定點處,電壓常數方程可以是僅含v的方程,勢函數V的具體形狀如圖3所示,可以發現兩側的勢阱是非對稱的,這更有助于FHN神經元非線性系統,在外界弱信號的驅動下,在靜息態到激發態躍遷；同時勢壘的高度也可以通過調節參數b來調整,該性質可以實現隨機共振的自適應響應。

圖3 勢函數示意圖

通過分析可以發現FHN神經元具有很好的非線性特性,在外界的信號的驅動下,可以實現不同勢阱間的躍遷,這有利于對不同能量態的弱信號進行篩選,以實現信號的增強與復原。但對由于單個神經元的魯棒性和系統的可表征性能都存在一定的缺點,因此受大腦的神經系統網絡機制啟發,本文提出通過概率隨機重連的方法構建小世界神經網絡,提高系統的穩定性。

1.2 WS小世界網絡

在人類的大腦內,神經元之間通過突觸連接構成了復雜的神經元網絡,以此實現各種各樣的功能。近些年,通過對大腦大量的生理實驗,發現生物神經元之間具有小世界拓撲結構特性,這表明復雜的神經元網絡的各個節點之間并沒有很復雜的連接通道,相反,他們只有很少的連接間隔。基于這種特性,我們構建一個以FHN神經元為節點的小世界網絡,各個節點之間具有如下規則,網絡中的任一FHN神經元節點以及順時針連接最近節點的邊,通過設置節點之間的重連概率p,重新建立此節點與網絡中任意其他節點的連接,且不允許和已經存在的連接重合,沿著網絡的順時針方向不斷的重復這個過程,建立基于概率p的連接。通過設置不同的連接概率,可以得到不同復雜程度的連接網絡,設置了一個節點數為20,每個節點與相鄰的4個節點互聯,與其他節點連接概率p分別設置為0、0.2、1,具體如圖4所示。

圖4 小世界網絡示意圖

本文在Strogats和Watts提出的小世界網絡結構基礎上[24],提出使用概率隨機重連的方法構造一個包含20個FHN神經元節點,重連概率為0.2的小世界神經網絡,其動力學方程的具體形式如式(3)所示:

式中:下標i表示網絡中神經元的標號,即i∈[1,20]；vi和ωi分別表示第i個神經元的膜電位和恢復變量；表示外界輸入刺激,i表示均值為0,方差為σ的高斯白噪聲；表示神經元之前的耦合項,表示了神經元i受到其他神經元輸入的突觸電流,具體形式如式(4)所示:

式中:αi,j表示耦合神經元之間的連接強度,與耦合神經元距離成反比；Ci,j是一個神經元之間的連接矩陣,Ci,j＝1表示是神經元之間存在突觸連接,Ci,j＝0表示神經元之間不存在突觸連接。

將外部刺激施加到小世界網絡中的某一FHN神經元上,并改變噪聲強度,然后觀察網絡中各神經元脈沖發放狀態,外部刺激信號和噪聲的具體信息如式(5)所示

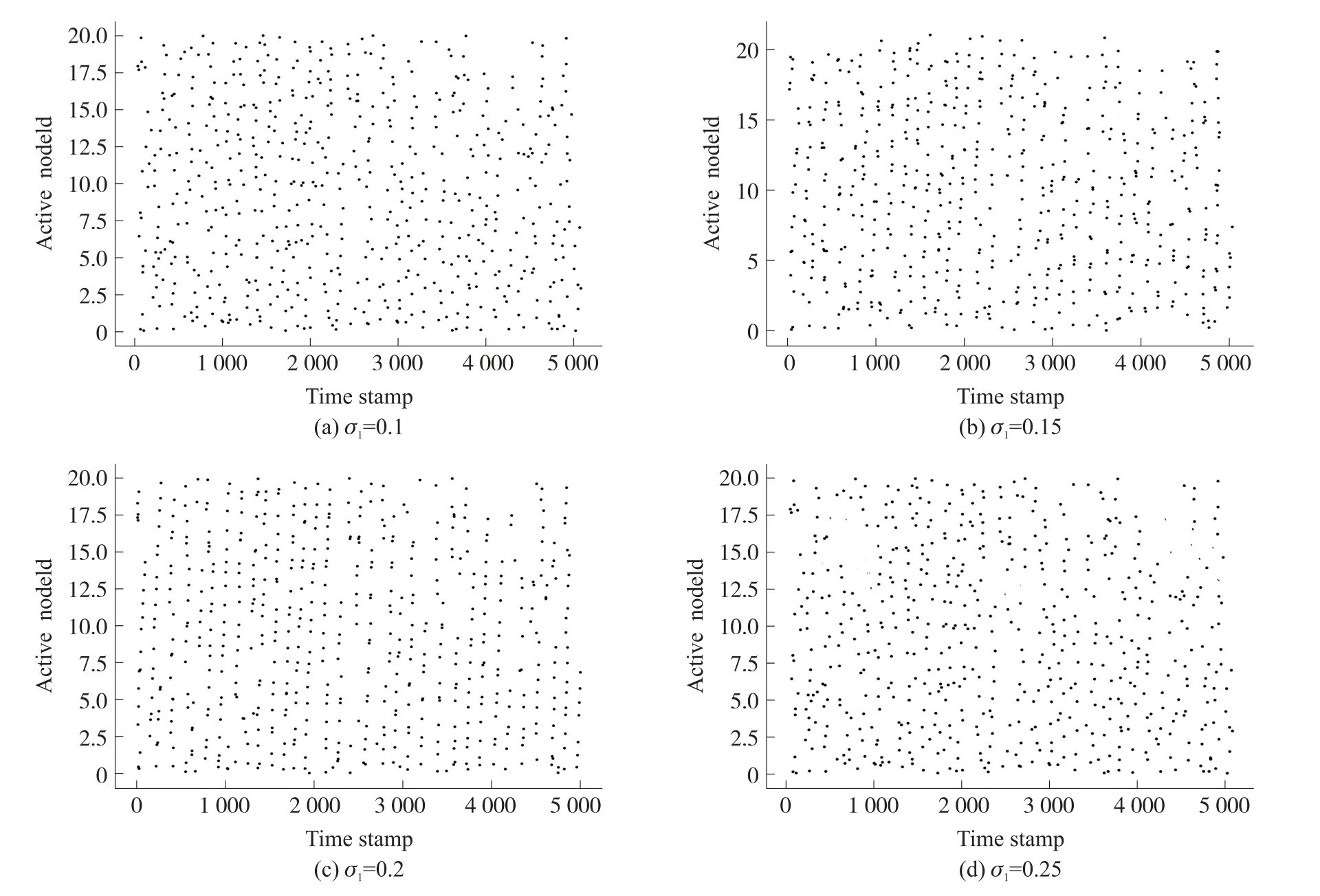
圖5 不同噪聲強度下神經元脈沖發放示意圖

1.3 性能評價指標

目前對隨機共振的性能衡量,主要涉及針對周期隨機共振的信噪比、信噪比增益和駐留時間分布,以及針對非周期隨機共振的相干函數、相關系數及基于信息理論的相關測度指標,為了使評價指標具有更一般性,本文采用基于輸入/輸出的互相關測度,將歸一化后的互相關系數作為性能評價指標,具體形式如下

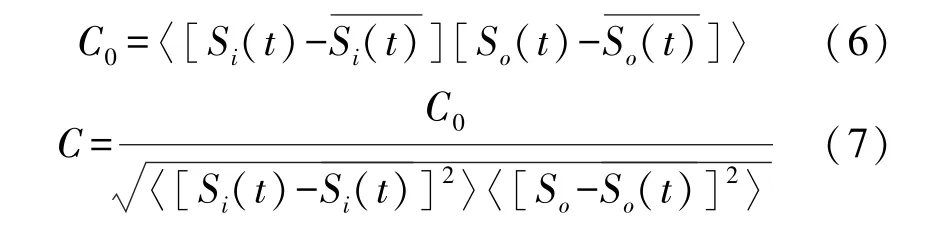
式中:Si(t)表示系統輸入信號,表示輸入信號均值；So(t)表示系統輸出信號,表示輸出信號均值；C0表示互相關系數,C表示歸一化后的互相關系數。

通過改變小世界網絡FHN神經元結點個數,并根據式(7)計算輸入信號和輸出信號的歸一化互相關系數隨著噪聲強度的變化；可以發現在同等噪聲強度下,節點數目的增加在一定程度下可以提高輸入信號和輸出信號的互相關系數；另外,在節點數目一定的條件下,當噪聲強度在一定范圍內,互相關系數會逐漸增大,但當噪聲強度大于一定值后,輸入信號和輸出信號的互相關系數會不斷降低,這種現象也是非常符合隨機共振的特性,具體如圖6所示。

圖6 互相關系數變化示意圖

為了有效利用小世界網絡中各個FHN神經元節點的共振輸出,同時為了避免單個節點信息的異常輸出,本文實時計算單個神經元節點輸入信號與輸出信號的互相關系數,互相關系數過低的異常節點輸出信息舍棄,基于此提出了一種網絡基于互相關系數的均值輸出融合策略,具體如式(8)所示。

式中:N表示小世界網絡中神經元節點的個數。

2 實驗結果與分析

為驗證本文提出方法的有效性,分別對單頻周期信號、多頻周期信號、變頻非周期信號以及高低電頻信號進行了相對應的實驗。根據實驗條件,小世界網絡的實驗參數設置為神經元節點數分別為5、9、13,重連概率為0.2,具有連接關系的神經元節點間耦合強度設置為0.01；神經元的參數可設置為εv＝0.01,εω＝1,b＝1。并根據系統參數的不同對實驗結果進行定性與定量的分析,為了證實本文方法應用的廣泛性和有效性,將常見的信號分為周期信號(其中包含單頻周期信號與多頻周期信號),和非周期信號(其中包含非周期變頻信號和高低電平信號)；對于周期信號,不僅需要對輸入信號和輸出信號的互相關系數進行分析,同時還需通過頻譜分析,以驗證隨機共振系統是否可以在保證輸入信號在噪聲干擾下對弱信號增強的前提,并能保證弱信號的主要頻率不變；對于非周期信號,由于信號的頻率參考意義不大,所以本文主要分析了輸入信號與輸出信號的歸一化互相關系數,以完成整體系統性能的分析。

本文首先進行輸入信號幅值為0.5,頻率為0.2的正弦弱信號在噪聲干擾下的隨機共振實驗,輸入信號的具體形式如式(9)所示。

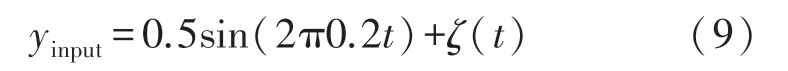
式中:ζ(t)為均值為0,方差為0.1的白噪聲。將該信號輸入到本文提出的基于FHN神經元小世界網絡的隨機共振系統,實驗結果如圖7所示,其中圖7(a)為對應的原始信號,從圖7(b)中可以發現,由于噪聲的作用,原始信號幾乎被湮沒,而圖7(c)輸出的實驗結果圖中可以直觀的發現原信號得到了很好的還原,同時信號強度也得到了增強；頻率譜圖如圖7(d)所示,可以看出信號頻率也得到了有效的提取。

圖7 單頻周期信號實驗結果

為了進一步證明提出的方法對于周期弱信號的有效性,本文使用組合的不同幅值和頻率的原始正弦弱信號,并加入一定強度的高斯白噪聲,對系統進行測試,其具體形式如式(10)所示。

多頻周期信號的處理結果如圖8所示,從圖8(a)原始信號、圖8(b)帶噪聲信號、圖8(c)輸出信號的實驗結果中可以直觀的看到,帶噪聲信號通過小世界網絡非線性系統之后,帶噪聲信號得到較好的還原與增強,使輸出信號與原始信號有較強的一致性；同時通過圖8(d)的頻譜圖,可直觀的看到三個不同頻率的峰值,它們分別是fs＝0.2 Hz,fs＝0.4 Hz,fs＝0.8 Hz,這也與原始信號中存在的三個頻率對應,說明本文方法在多頻周期信號中仍然有很好的性能。

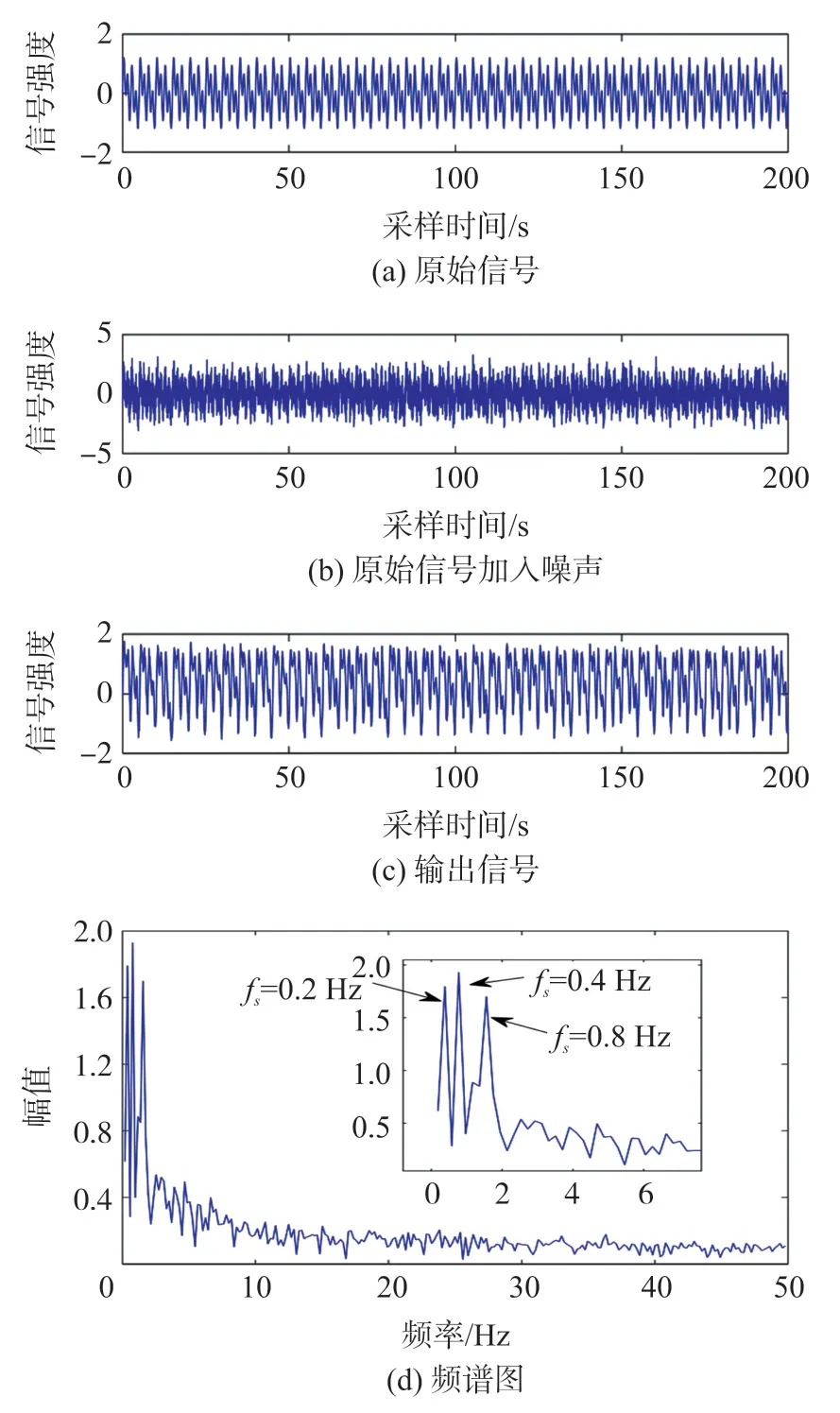
圖8 多頻周期信號實驗結果

另外,由于現實世界的多變性,周期信號只是常見信號的一種類別,各種非周期信號可能更加普遍的存在,而非周期變頻信號和高低電平也是現實中較為常見的信號,因此以非周期信號作為實驗對象,也更能證明本文方法在弱信號增強還原方面的有效性和實際應用的價值。

其中,非周期變頻信號的具體形式如式(11)所示

變頻非周期信號的處理結果如圖9所示,其中輸入的原始非周期變頻信號形式如圖9(a)所示,信號的頻率變得越來越高,呈現出一種非線性變化,將其加入強度為0.1的高斯白噪聲,其波形圖如圖9(b)所示,然后將帶噪聲的信號輸入到由FHN神經元構建的小世界網絡非線性系統中,然后其輸出信號如圖9(c)所示,雖然波形仍然有一些噪聲干擾,單輸入信號的波形依然較好的得到了還原,并且輸入信號的信號強度也得到了進一步的增強。同時,我們將小世界網絡中的每一個神經元的響應圖進行了可視化,如圖9(d)所示,每一個神經元都可以在一定程度上對信號進行增強和還原,但相對來說誤差會稍微大一些,但經過均值融合之后得到的最終結果會有進一步的提升,這也證明通過對神經元進行集群操作可以更好地提升系統的性能和魯棒性。

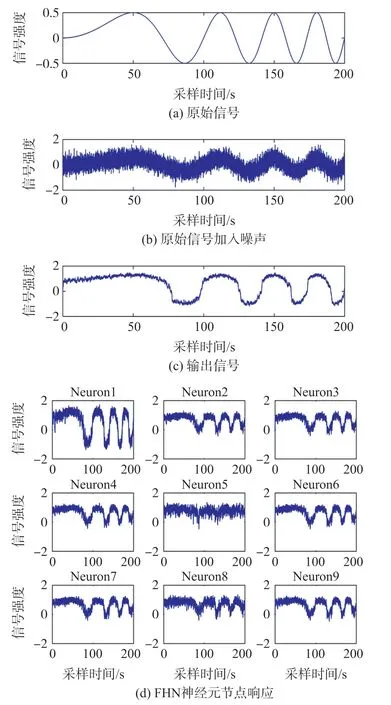
圖9 變頻非周期信號實驗結果

圖10 高低電平信號實驗結果

最后,考慮到高低平信號在數字電路中具有很廣泛的應用,所以如何對電平信號進行噪聲的處理具有重要的意義,傳統的方法多通過濾波處理,但這同時可能也會導致電平信號的錯誤處理,因此本文通過小世界網絡構建的非線性系統與含噪聲的高低微弱電平信號形成隨機共振,有效的利用噪聲信號的能量,以實現對含噪聲弱信號的還原與增強,這能保證電平信號在傳輸處理過程中即使受到噪聲干擾,依然能保持信息傳遞的準確性,具體實驗結果如圖10所示,可以發現系統的輸出,在噪聲的干擾下很好的還原了輸入信號的高電平和低電平,并且輸入信號的幅值被放大,高電平和低電平的差異也進一步得到了區分。

通過本文提出的小世界網絡非線性系統方案與被噪聲干擾的弱信號的增強復原方法,實現非線性系統、弱信號、噪聲三者的共同作用,達到了很好的隨機共振效果,對在噪聲干擾下的輸入弱信號,較好地實現了弱信號的增強還原。雖然從上述定性的角度,可以發現該方案對周期信號和非周期信號均有較好的實驗效果,為了進一步說明方案的有效性,本文從定量的角度,對系統參數做了更加深入的分析,以歸一化后的互相關系數作為評價指標,通過調整小世界網絡的FHN神經元節點數目,觀察系統性能的變化。

根據表1可以得到不同輸入信號,在經過不同小世界網絡節點數目計算的互相關系數,神經元節點數目越多,互相關系數的值也相應會越大,比如N＝13時,單頻周期信號、多頻周期信號、非周期變頻信號以及高低電平信號的互相關系數值可以分別達到0.987、0.966、0.957、0.961,在三組不同的小世界網絡神經元節點數目,結果都傾向于最優；當N＝5和N＝9時,雖然相對于N＝13時性能有所下降,但系統對于弱信號的復原與增強能保持較高的互相關系數,其實驗結果也基本與圖6的實驗現象保持一致,證明了本文方法的有效性。

表1 輸入與輸出信號的互相關系數

3 結論

本文依據生物神經機制,首先研究了FHN神經元非線性系統、弱信號和噪聲三者的隨機共振特性,其次,受生物神經元網絡的啟發,構建了以FHN神經元為節點的小世界網絡。通過對FHN神經元特性的分析和小世界網絡在噪聲驅動下的隨機共振特點,并分別以周期和非周期帶噪聲弱信號作為待檢測信號,對系統進行了驗證,證明了本文提出方法的有效性。隨著網絡神經元節點數目的增加,在一定程度上可以提高系統輸入信號和輸出信號的互相關系數,并提高系統的魯棒性。但網絡的最優神經元節點數,將是接下來研究的重點；另外,小世界網絡中神經元節點之間的突觸連接形式,也有待進一步研究。通過本文的研究,為生物神經網絡為什么具有極強的去噪聲能力和弱信號檢測性能提供了一種新的解釋,同時為強魯棒性的隨機共振和實際應用也提供了一個新的思路。