基于鯨魚優(yōu)化算法的失配濾波器設計

單文童，欒曉明

(哈爾濱工程大學 信息與通信工程學院，黑龍江 哈爾濱 150001)

0 引言

改善二相編碼旁瓣特性的常用方法是波形設計和旁瓣抑制。波形設計分為2種，一種是通過設計旁瓣性能比較好的碼元來達到實際應用需求；另一種是選擇自相關性能較好的編碼信號，但此類方法會受到較多限制，并且大部分實際工程中很難應用到此類方法設計出的編碼。如果確定發(fā)射端編碼信號，但回波信號旁瓣電平仍然不理想時，還可以設計相應的失配濾波器來進一步降低旁瓣。設計失配濾波器時通常用峰值旁瓣電平(Peak Sidelobe Level，PSL)作為適應度函數，通過循環(huán)迭代可以獲得更好的濾波器系數，如最小二乘法[1-2]、線性規(guī)劃法[3-4]、神經網絡法[5]及碼型捷變法[6]等。

文獻[7]利用迫零算法設計二相碼的失配濾波器，若在迭代過程中步長因子選擇不當則該算法收斂性能較差，從而導致求解的濾波器系數不能達到理想效果。文獻[8]討論了基于二階錐規(guī)劃的旁瓣抑制濾波器設計，但是對大時寬帶寬積信號的濾波器系數進行優(yōu)化時，求解很困難。文獻[9]提出了基于雞群優(yōu)化算法失配濾波器設計方法，但該算法需調整的參數設置較多，不恰當的參數會導致算法收斂速度較慢、收斂精度較差，從而導致結果不理想。文獻[10]討論了基于CLEAN算法的二相編碼信號脈壓副瓣抑制方法，但如果CLEAN門限選擇不當，則不能有效降低m序列、巴克碼等二相編碼信號的脈壓副瓣。

文獻[11]提出了鯨魚優(yōu)化算法(Whale Optimization Algorithm，WOA)。本文針對WOA收斂速度慢的特點，提出一種隨著迭代次數增加收斂因子非線性變化的算法——NCF-WOA，具有更快的收斂速度和更好的收斂精度，從而能快速找到全局最優(yōu)點。利用NCF-WOA對常用二相碼求失配濾波器，與傳統(tǒng)的匹配濾波器方法相比，失配濾波器處理得到的主旁瓣比有明顯提高。

1 鯨魚優(yōu)化算法

2016年，澳大利亞學者Mirjalili提出了一種新型群體啟發(fā)式智能優(yōu)化算法——WOA。該算法原理結構相對簡單、需要設置的參數較少，且具有跳出局部最優(yōu)的強大能力。在多元函數求解方面比粒子群優(yōu)化(Particle Swarm Optimization，PSO)算法具有更高的求解精度[11]，它通過模擬鯨魚狩獵行為抽象出下面3種函數。

1.1 包圍獵物

每一只鯨魚都對應著一個個體，個體在搜索空間中的位置都有相應的解。每只鯨魚都能夠通過回聲來確定獵物的位置并對其進行包圍，鯨魚的位置更新表達式如下：

X(t+1)=Xp(t)-A·|C·Xp(t)-X(t)|，

(1)

式中，rand1和rand2代表[0,1]內的隨機數；a稱為線性收斂因子，即：

(2)

式中，t為當前迭代數；tmax為最大迭代次數。

1.2 Bubble-net攻擊

收縮功能通過式(2)隨著線性收斂因子a的逐步減小來實現，同時A的收斂范圍也隨著線性收斂因子a減小而減小，即隨著a從2減小到0時，A的收斂范圍為[-a,a]。螺旋更新位置如下：

X(t+1)=XP(t)+D·ebr·cos(2πr)，

(3)

式中，第i只鯨魚與獵物之間的距離D=|Xp(t)-X(t)|；b為螺旋常數；r為在[-1,1]范圍內的隨機數。

1.3 隨機搜索

當|A|>1時，代表鯨魚個體在包圍圈外部運動，其數學模型為：

X(t+1)=Xrand(t)-A·|C·Xrand(t)-X(t)|，

(4)

式中，Xrand表示目前群體當中隨機選取的個體位置。

2 改進鯨魚優(yōu)化算法

WOA作為一種基于種群迭代的元啟發(fā)式算法，處理好該算法開發(fā)和探索能力的協(xié)調性具有很高的優(yōu)先級。探索能力表示當前群體對搜索域的空間范圍有著更高的要求；而個體利用目前掌握的信息對解空間的某些鄰域進行局部搜索則是開發(fā)能力的主要體現，開發(fā)能力的優(yōu)劣直接影響著算法的收斂速度[12]。

WOA的探索和開發(fā)能力取決于收斂因子震蕩變化的程度。在基礎WOA中，線性時變策略在實際中不能完全反映WOA的優(yōu)化搜索過程。應該期望前期WOA在擁有良好的全局搜索能力的同時收斂速度也可以保持在一個較高的水準。搜索后期在保證WOA擁有較快的收斂速度的同時避免算法陷入局部最優(yōu)。因此，本文提出一個收斂因子非線性變化的更新表達式：

(5)

式中，a表示收斂因子；tmax表示設定的最大迭代次數；μ，α稱為非線性調節(jié)系數。該算法使用線性收斂因子和非線性收斂因子迭代100次時的收斂變化曲線如圖1所示。當μ=3，α=0.72時，可以看到非線性收斂因子使該算法在收斂速度上有明顯提升。

圖1 不同收斂因子下算法迭代變化趨勢Fig.1 Algorithm iteration change trend under different convergence factors

3 旁瓣抑制濾波器的設計

3.1 設計原理

失配濾波器的大多數優(yōu)化工作僅將峰值旁瓣作為單個目標，本文提出了集成旁瓣能量的概念，并建立了一個使集成旁瓣能量最小的功能優(yōu)化模型。針對不同的應用，給出了2種不同的設計標準(最小旁瓣標準、最小損耗標準)，它們可以靈活地設計具有不同預期響應的失配濾波器。此外，將PSL、失配濾波損失(MMFL)和積分旁瓣電平(ISL)表示為凸函數，并使用線性加權求和將這些凸函數的線性組合用作新的多目標函數的目標函數。該方法可以根據實際工程需求靈活調整不同指標之間的權重，從而設計出最佳失配濾波器。

假定相位編碼信號碼長為P，時寬為T。對回波進行采樣，每個碼元內采集一個點，得到復采樣序列{xk}，其中k=0,1,…,P-1。設計的M階濾波器的權系數用{wm}表示，m=0,1,…,M-1，在約束范圍內，當M>P時處理效果會更好。因為旁瓣能量會被分散到其他旁瓣上，主副瓣比也隨之提高。但是實際工程應用中，因為硬件資源的限制，濾波器階數通常不會超過信號碼長的2倍。{sm}是由{xk}在兩端進行補零得到的信號序列，寫成向量形式為[13]：

s=(s0,s1,…，sM-2,sM-1)T=

(0,0,…,x0,x1,…,xP-1,0…0)T，

(6)

則濾波器響應為：

(7)

式中，當n-i<0以及n-i>M時,sn-i=0。

式(6)用向量表示為：

Y=XHW，

Y=(y0,y1,…,y2·M-2)T，

W=(w0,w1,…,wM-1)T，

設當n=M-1時信號通過濾波器的主峰[14]，最小PSL濾波器是對PSL進行限制，并且使其最小化。需要滿足的約束條件如下：

s.t.yM-1=1。

(8)

在此信號模型下，最小ISL濾波器滿足下式：

s.t.yM-1=1。

(9)

與匹配濾波不同，信號通過失配濾波器必然會造成信噪比損失，用MMFL來衡量其大小[15]：

(10)

通常情況下，主瓣的輸出要求約束為一個定值：

(11)

同時，對其進行歸一化處理，則式(8)可簡化為：

(12)

在實際工程設計中，失配濾波損失越小代表著處理效果越好，但是失配濾波損失與PSL是互相約束的，不可能同時取最優(yōu)值[16]。因此，實際情況是在限制失配濾波損失不超過某一期望最大值α dB時：

LMMFL=αdB，

使PSL最小的折衷過程，即：

(13)

3.2 多目標優(yōu)化模型

多目標優(yōu)化是指需要同時優(yōu)化多個目標的情況。當需要在幾個相互矛盾的目標之間進行權衡時，采用多目標優(yōu)化方法往往會得到理想的結果。在多目標優(yōu)化問題中，可以使用線性加權求和。該方法通過將要優(yōu)化的目標函數的線性組合作為新的目標函數，形成一個新的優(yōu)化問題。通過解決該優(yōu)化問題，獲得優(yōu)化結果。

用于線性加權系數向量為v：

(14)

設目標函數向量f為：

(15)

式中，f的第1個目標函數對應峰值旁瓣；第2個目標函數對應積分旁瓣能量。故有以PSL、MMFL和ISL的線性加權求和得到的結果為目標函數的優(yōu)化問題，如式(16)所示：

s.t.yM-1=1

(16)

式(16)可以通過WOA求解出相應的函數值，其實際意義是與信號序列對應的濾波器系數[17]。WOA通過對比鯨魚個體適應度函數值的大小來判斷濾波器權值的優(yōu)劣。函數值越小，對應的失配濾波器的權值越符合設計要求[18]。相比上述算法，通過本文提出的NCF-WOA對式(12)進行求解時，更容易找到全局最優(yōu)值，即最優(yōu)失配濾波器系數。

4 設計仿真

二相編碼信號常用的二元偽隨機序列有巴克碼和最大長度碼(m序列)，因此以常用的13位巴克碼和在最大失配濾波損失LMMFL=0.9 dB時針對碼長P取127，255的m序列為例，分別采用改進后的WOA設計了不同階數的旁瓣抑制失配濾波器，并進行了脈壓仿真，其中取個體數量n=100，d取值即為所求失配濾波器長度，參數μ=5，α=0.74。取v=(1,0)T，程序隨機運行100次并記錄下每次運行的最優(yōu)解，濾波器的系數就是其最優(yōu)解。仿真結果分別如圖2、圖3和圖4所示。

圖3中，127位m序列碼自相關的PSL為-20.5 dB，對其進行相同碼長的失配濾波器處理得到的PSL為-26.3 dB，通過2倍碼長的失配濾波器處理得到的PSL為-30.0 dB。

圖4中，255位m序列碼自相關的PSL為-24.1 dB，對其進行相同碼長的失配濾波器處理得到的PSL為-30.5 dB，通過2倍碼長的失配濾波器處理得到的PSL為-38.3 dB。

從仿真結果可以看出，與傳統(tǒng)的匹配濾波脈壓處理相比，利用改進后的鯨魚優(yōu)化算法設計失配濾波器，性能均有顯著改善，且性能隨著濾波器階數的增加而提高。文獻中算法處理得到的PSL對比結果如表1所示。

圖2 巴克碼的脈壓結果Fig.2 Barker code pulse compression result

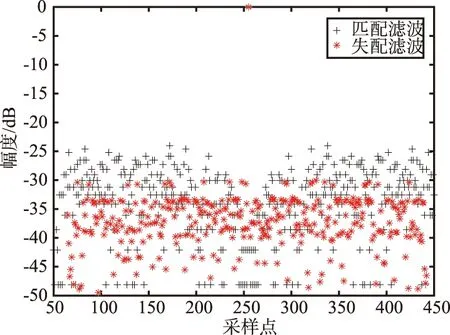
(a) N=P時的失配脈壓結果

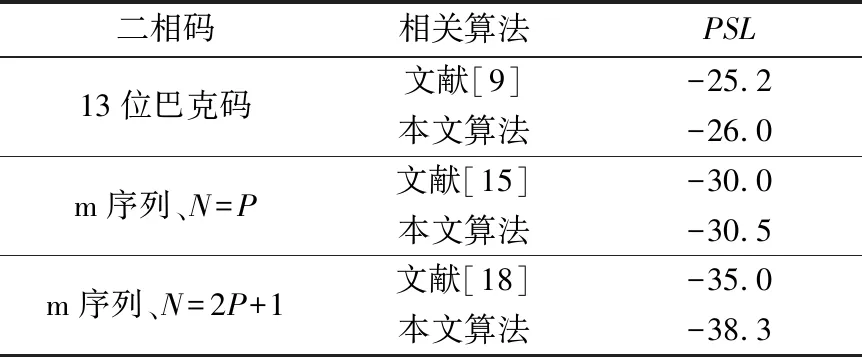
表1 相關算法PSL對比Tab.1 Comparison of peak sidelobe level (PSL ) obtained with different correlation algorithms 單位：dB

5 結束語

在對相位編碼失配濾波器設計很難通過常規(guī)途徑得到對應的濾波器權值問題的背景下，本文對WOA中權值確定方法進行了改進。提出了采用非線性收斂因子，使該算法在迭代過程中收斂速度更快，精度更高。本文對巴克碼、127位m序列碼以及255位m序列碼進行了仿真。仿真結果表明，在進行旁瓣抑制濾波器設計時，采用該改進方法能夠實現濾波器系數的快速收斂，所求得失配濾波器具有較好的性能，能夠滿足實際應用需求。