一種基于信息熵的加權混合預測模型

單曙兵 張紹華

（1.中匯信息技術（上海）有限公司 上海市 201203 2.上海計算機軟件技術開發中心 上海市 201112）

1 引言

在人工智能領域已經存在多種預測模型來解決不同的預測問題[1]。如傳統的回歸模型主要解決線性預測問題；而針對時間序列歷史數據，可以采用自回歸模型AR、移動平均模型MA 以及其他各種組合和變形的時間序列模型；神經網絡模型和深度學習模型用于解決非線性預測問題等等。但單一的預測模型難以解決不同場景下復雜的預測問題，因而已經有諸多學者將兩種或多種預測模型構成混合模型來取得更好的預測效果[2-4]。

張永峰等人將一維卷積神經網絡模型與雙向長短期記憶模型進行混合用于預測機器設備的剩余壽命，該模型不但可以有效地抽取時間序列上的特征，還可以產生更多的訓練樣本，從而提升預測精度[5]。王英偉等提出一種將ARIMA 和LSTM 混合的時間序列模型，實驗結果表明該混合模型優于單一模型的預測[6]。郭海燕等提出了一種基于模擬退火算法優化BP 神經網絡的預測模型，從而實現較好的負荷預測[7]。溫海茹等提出將深度卷積神經網絡和長短期記憶網絡混合的預測模型，該方法在C-MAPSS 數據集上進行了驗證，其結果優于單一的CNN 和LSTM 模型[8]。袁全等提出一種基于時間序列與天牛須搜索算法改進BP 神經網絡的組合預測模型，仿真結果表明提出的混合預測模型好于單一模型[9]。黃偉建等提出將STAQI 模型和門循環單元模型進行混合，該模型用于預測空氣質量其結果在均方根誤差方面優于傳統的深度學習模型[10]。上述模型都是通過一定的方法提升預測的精度，而如果在不同的預測階段將預測精度最好的兩個或多個模型進行混合，使其各自發揮解決不同預測問題的優勢，實現更為精準的預測。因此本文提出一種由互信息和信息熵共同決定權重的加權混合預測模型。

本文所做的貢獻如下：

（1）提出一種全新的由互信息和信息熵共同決定權重的加權混合預測模型，并命名為MPR；

（2）研究并討論了如何選擇待混合的模型，比較了經典的權重的確定方法優劣；

（3）通過真實的數據，并引入9 個基準模型從預測精度和方差比較了混合模型的優勢。

2 加權混合預測模型

在本節中，我們將提出一個全新的混合模型MPR，它可以混合兩種預測模型。公式（1）是MPR 模型的數學表達式，V 是預測值，w 是權重，A、B 表示預測模型。

在信息論中，熵可以量化信息源的信息不確定性[11]。在公式（1）中，模型A 和模型B 是信息源，而A 和B 作為信息源給出的信息實際上是預測準確度（例如1%，2%，...100%）。基于熵的定義，在我們的研究中，信息源的準確性越高，熵越小。但是，熵是對稱的，也就是說，信息源的準確性差也導致熵的值小。為了解決這個問題，本文使用加權熵來降低精確度較低信息源的影響。并且，在本文的混合模型MPR 中涉及兩個信息源，所以它們平均相互信息是相同的。因此,如果一個模型的平均相互信息與信息源的加權熵之比更大，則相應的信息源具有更準確的信息。在這個情況下，該信息源即預測模型在混合模型中的相關權重應該更大，也就是說混合模型整合了每個預測模型中更為準確和穩定的預測部分。

基于以上討論，權重確定如下：我們首先使用訓練數據集完成A 和B 模型的訓練，然后將訓練后的A 和B 模型分別使用驗證數據集進行預測。這兩個模型獲得的結果的準確性是根據公式（2）計算的。在公式（2）中，aij是使用第j 個模型（即第j 個信息源）預測第i 個驗證數據的準確性。Ri代表第i 個驗證數據的實際值。Fij表示第j 個模型對第i 個驗證數據預測值。

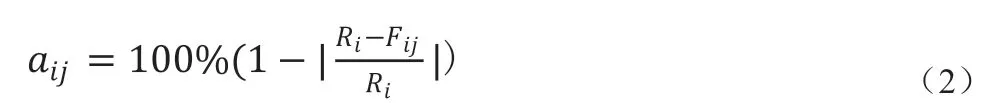
對于m 項驗證數據，第j 個模型將產生m 個相應的精度值。如果使用列向量ATj=（a1j，a2j，...amj）T 表示第j 個模型的精度，則所有模型的精度值都可以用矩陣Amn 表示，如公式（3）所示。

表1：常見的9 個預測模型

圖1：MPR 與9 個基準模型的預測結果對比

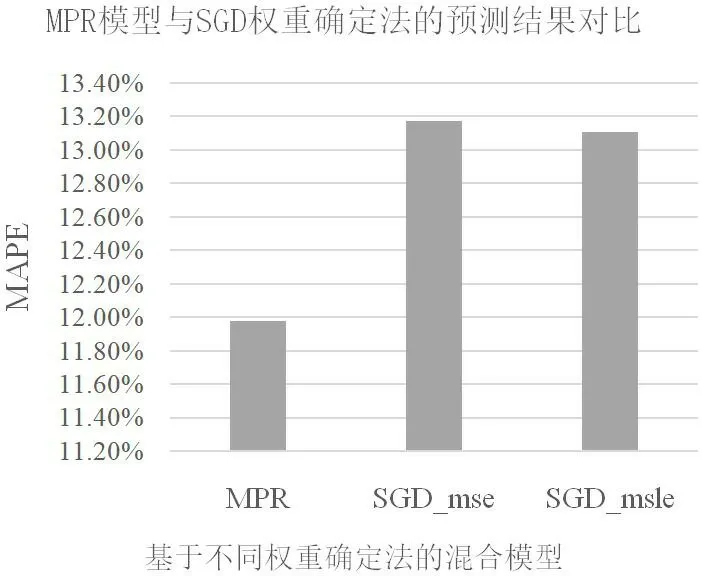
圖2：MPR 模型與SGD 權重確定法預測結果對比

在矩陣Amn中計算每個精度值的出現次數（注意：精度值是實數，因此在計算精度值的出現次數時，我們僅考慮其整數部分（例如87%而不是87.15%）并得到等式（4）所示的Rmn，其中，rij代表第j 列中aij（其整數部分）的出現次數。

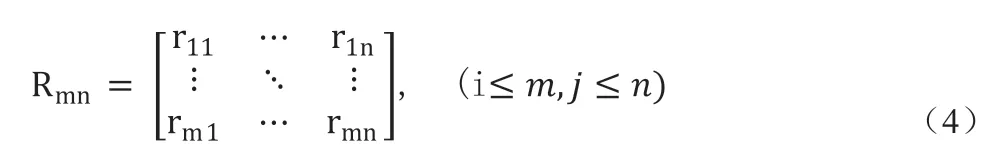
矩陣Rmn 中的每個元素將被代入到方程式（5），以分別獲得A 模型和B 模型的加權信息熵。如上所述，加權熵為了使精度更高的信息源在混合模型中更加重要。我們可以計算方程（5）的加權熵。在式（5）中，Ej 是第j 個模型的加權信息熵（即，第j 個信息源）.wij'與pijlogpij對應，Nj 表示在矩陣Amn的第j 列中aij大于準確率X%的數量，其中X 依據實際需要取適當值。pij的第j 列中是rij的出現的概率，其中M 表示第j 列上rij的總和。

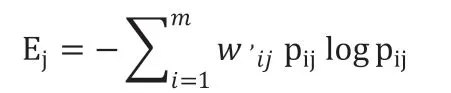
其中，

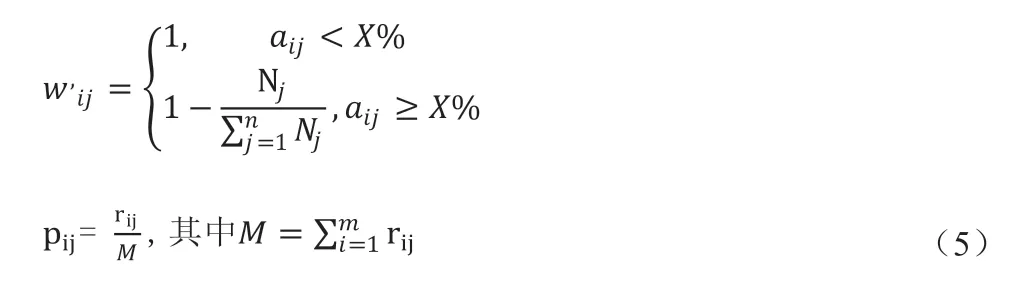
表3：MPR 與9 個基準模型的預測結果方差對比

表4：MPR 模型與SGD 權重確定法預測結果的差對比

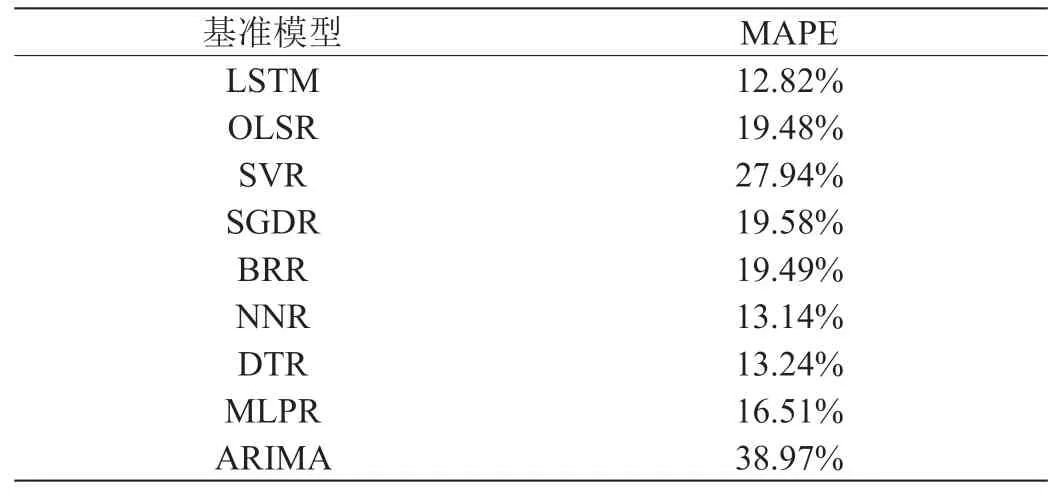
表2：9 個基準模型的預測結果

計算用于確定混合模型中權重的平均互信息的過程如下：如果ak=al，則定義階躍函數UN(ak, al)=1，否則，UN(ak, al)=0，其中ak和al(k=l)是矩陣Amn 中的兩行。定義ci = 1 + ∑mj,j≠iUN(ak, al)(1 ≤i ≤m）,可以得到向量CmT=（c1，c2，....cm）T。應用公式（6）獲得兩個信息源的平均互信息，其中J 和J’分別代表兩個信息源。

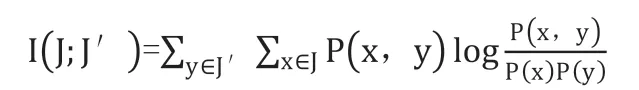
其中，

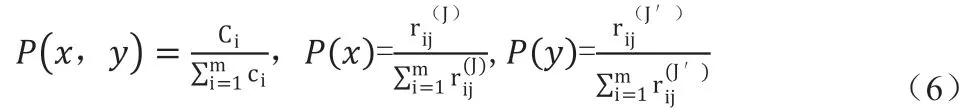
根據前文的討論，MPR 模型中每個組成模型（即信息源）的權重是平均互信息與其熵的比值。第j 個信息源的權重將由等式（7）計算。在等式（7）中，I 是平均互信息，而Ej 表示第j 個源的加權熵，Z 是用于歸一化所有基本算法的權重以確保所有權重之和為1 的參數。

3 實驗結果

為了評估預測結果的質量，本文利用等式（8）所示的MAPE（平均絕對百分比誤差）[12]，其中At 為實際值，Ft為預測值。

在計算實驗中，我們采用9 種常用的預測模型（如表1 所示）作為基準。這些模型的某些應用可以在[13-14]中找到。它們代表7種不同類型的模型，包括廣義線性回歸，支持向量機，最近鄰居，高斯過程，決策樹，集成方法，神經網絡，時間序列模型和長期短期記憶。

使用提出的MPR 模型和表1 的9 個模型預測平臺訪問流量，現已有1年的平臺流量數據，并得知因素退出率、點擊密度、平均會話時間影響平臺的訪問流量，并將上述數據劃分為60%訓練集，20%的驗證集，20%的測試集進行實驗。依據經驗，公式（5）中的X 取70%，實驗結果如表2 所示。從表2 中可以看出，LSTM模型和NNR 模型的預測精度位于前兩位，選取這兩種模型，并使用公式1 到公式7 計算提出的MPR 模型的預測結果，并與表2 中模型結果進行了對比，如圖1 所示。從圖1 中可以看出，提出的MPR 模型的預測的MAPE 值最小，其預測精度明顯好于任何單一的基準模型。

此外，使用方差來評估所有模型的預測結果。表3 顯示了MPR 與9 個基準的預測結果的方差。MPR 在方差方面表現最佳，這表明MPR 能夠產生合理的結果。因而我們提出的MPR 混合預測模型整合了其組成部分的預測優勢，不僅對精度有所提升，其穩定性也有較大提升。

4 分析與討論

4.1 模型混合原則

在本文第2 節中MPR 模型混合了LSTM 和NNR，取得了良好的預測效果。但在進行模型混合時需要遵循兩個原則，一是模型的多樣性，二是預測表現。

4.1.1 多樣性

多樣性意味著混合的模型是不同的。因此，從統計學角度考察LSTM 和NNR 是否為不同的模型。為此，本文進行統計檢驗。由于通過算法獲得的預測結果的分布是未知的，因此應使用非參數檢驗。類似于Ablanedo-Rosas[15]的研究，我們使用Wilcoxon ranksum檢驗（秩和檢驗）確定兩個選擇的樣本是否具有相同的分布。在此，給出零假設：LSTM 和NNR 所獲得的預測結果總體相同。使用開源scipy 軟件用于通過調用stats.ranksums 進行測試，該測試的p 值為2.801e-106（<0.01）。因此，拒絕零假設，并確認LSTM 和NNR不是相似的模型。

4.1.2 預測性能

LSTM 和NNR 是實驗中表現最優的兩個模型，LSTM 是9 個基準模型中預測精度最高的，NNR 是9 個基準模型中方差最小的。而混合模型需要整合最佳性能模型。混合模型MPR 與9 個基準模型相比確實表現出最好的表現即精度最高并且方差最小。

4.2 不同權重方法的結果比較

某些優化算法，例如SGD（隨機梯度下降等）通常用于確定模型的權重。但是，這種方法不但是黑盒，而且很容易陷入局部最優[16]。如果很難獲得最佳權重，這會導致混合預測精度的折衷。本節使用SGD 算法確定方程（7）中的權重，并采用兩個損失函數包括MSLE 和MSE（均方誤差）分別實驗。圖2 中，SGD_mse 表示將具有MSE 損失函數的SGD 應用于確定權重的混合模型。SGD_msle 表示使用具有MSLE 損失函數的SGD 確定權重的混合模型。如表4 所示，平均方差也是最低的。

5 結論

本文提出了一個全新的混合預測模型。在預測中需要解決不同需求和場景問題，因此，單個模型無法提供令人滿意的預測結果。為了解決該問題，本文采用了基于互信息和信息熵的比值確定權重的混合模型，這不僅避免了混合模型中權重出現局部最優的問題，還具有更好的可解釋性并使得精度更高、穩定性更好的模型更加重要。

此外，實驗證明MPR 模型可以提供具有更好的準確性和方差的預測結果。在未來的研究中，計劃收集更多的數據集評估所提出模型的長期預測能力，以幫助進一步改善預測準確性。