基于系列圖譜回歸公式的螺旋槳推力計算

萬柳梅 于涵 耿建寧 姚帥 榮凱

（1.中船航海科技有限責任公司 北京市 100070 2.中國船舶重工集團公司第七〇七研究所 天津市 300131）

1 前言

一般有兩種途徑獲得螺旋槳推力，一是利用流體力學進行理論計算，另一是進行試驗直接測量。螺旋槳的理論計算方法現在還不完善，因此目前無論是進行螺旋槳設計，還是研究船舶操縱運動特性，都是采用試驗方法求螺旋槳的推力。在船舶駕駛模擬器、船舶自動控制仿真研究中建立船舶運動數學模型通常采用四象限法計算螺旋槳的推力[1][2]，該方法對螺旋槳前進中正車、前進中倒車、后退中進車、后退中倒車等各種工況計算精度高，但對螺旋槳的敞水試驗數據依賴大，且計算復雜，無模型試驗或試驗數據不詳的船舶使用該方法進行計算受到限制。

螺旋槳的圖譜通常用于螺旋槳的設計，圖譜設計法是根據螺旋槳模型敞水試驗所得到的圖譜或公式來確定實船螺旋槳主要參數和性能的傳統設計方法。當船舶螺旋槳的類型與尺寸確定之后，采用基于圖譜的回歸公式計算螺旋槳的推力精度高、計算簡便。當前世界上比較著名、應用交廣的性能優良的螺旋槳系列有：荷蘭的B 型螺旋槳、日本的AU 型螺旋槳和英國的高恩螺旋槳，B 型和AU 型螺旋槳適用于商船，高恩螺旋槳則適用于水面高速軍艦。

2 船舶運動數學模型

2.1 坐標系與符號

如圖1 所示，船舶運動數學模型采用兩種坐標系：固定坐標系O0X0Y0Z0和隨船坐標系Gxyz。其中固定坐標系的原點O0可以任意選擇，O0X0軸指向正北，O0Y0軸指向正東，O0Z0軸垂直向下為正X0O0Y0平面位于靜水面內；隨船坐標系Gxyz 的原點G 為船舶重心，Gx 軸指向船艏，Gy 軸指向右舷，Gz 軸垂直向下指向龍骨。在t=0時選取坐標系原點O0和G 的位置一致。

2.2 船舶三自由度運動模型

本文只研究船舶螺旋槳產生的力與力矩作用，因此僅在螺旋槳作用下船舶的三自由度MMG 模型如下[3]：

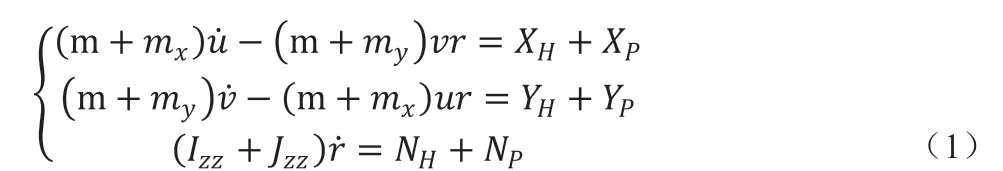
其中，m、mx、my、Izz、Jzz分別為船舶質量、附加質量和附加慣性矩；u、v、r 分別表示縱移速度、橫移速度與艏向角；分別表示縱向加速度、橫向加速度與艏搖角速度；XH、YH、NH為船舶水動力與水動力矩，XP、YP、NP為螺旋槳產生的力與力矩。

船舶水動力的計算見文獻[1]，本文不作介紹。

2.3 螺旋槳推力計算模型

考慮螺旋槳與船體間的相互作用，常規定距螺旋槳產生的推力和力矩可表示為：

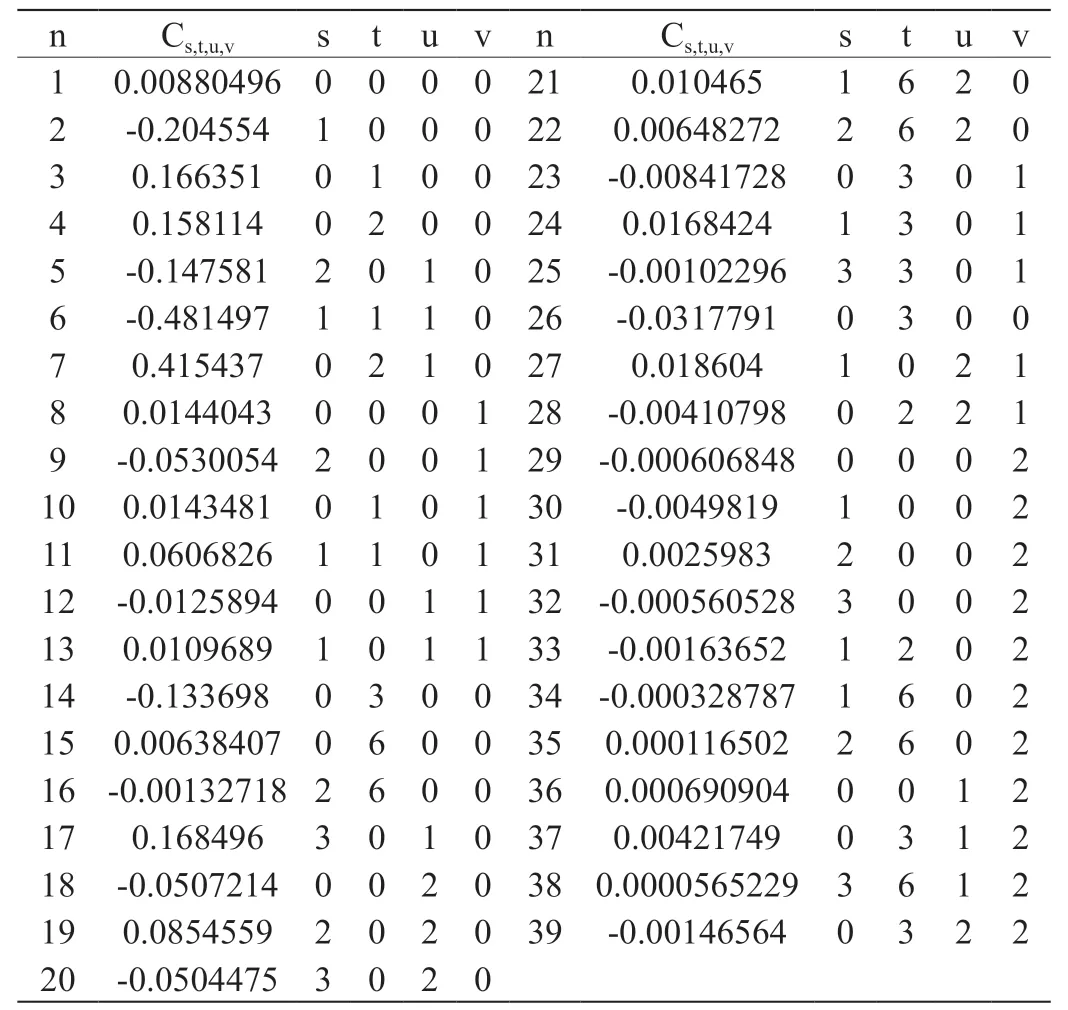
表1：B 系列螺旋槳回歸公式系數與指數

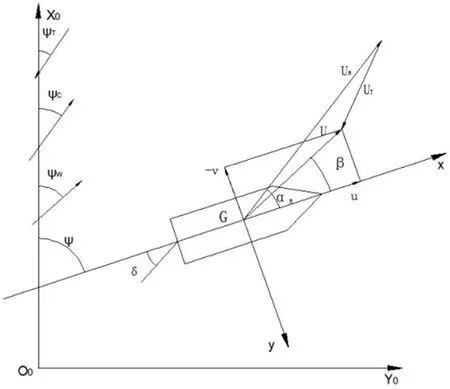
圖1：船舶運動坐標系

其中Kt(J)為螺旋槳的推力系數，船速，n-螺旋槳轉速，D-螺旋槳直徑，ω-伴流分數，t-推力減額分數。

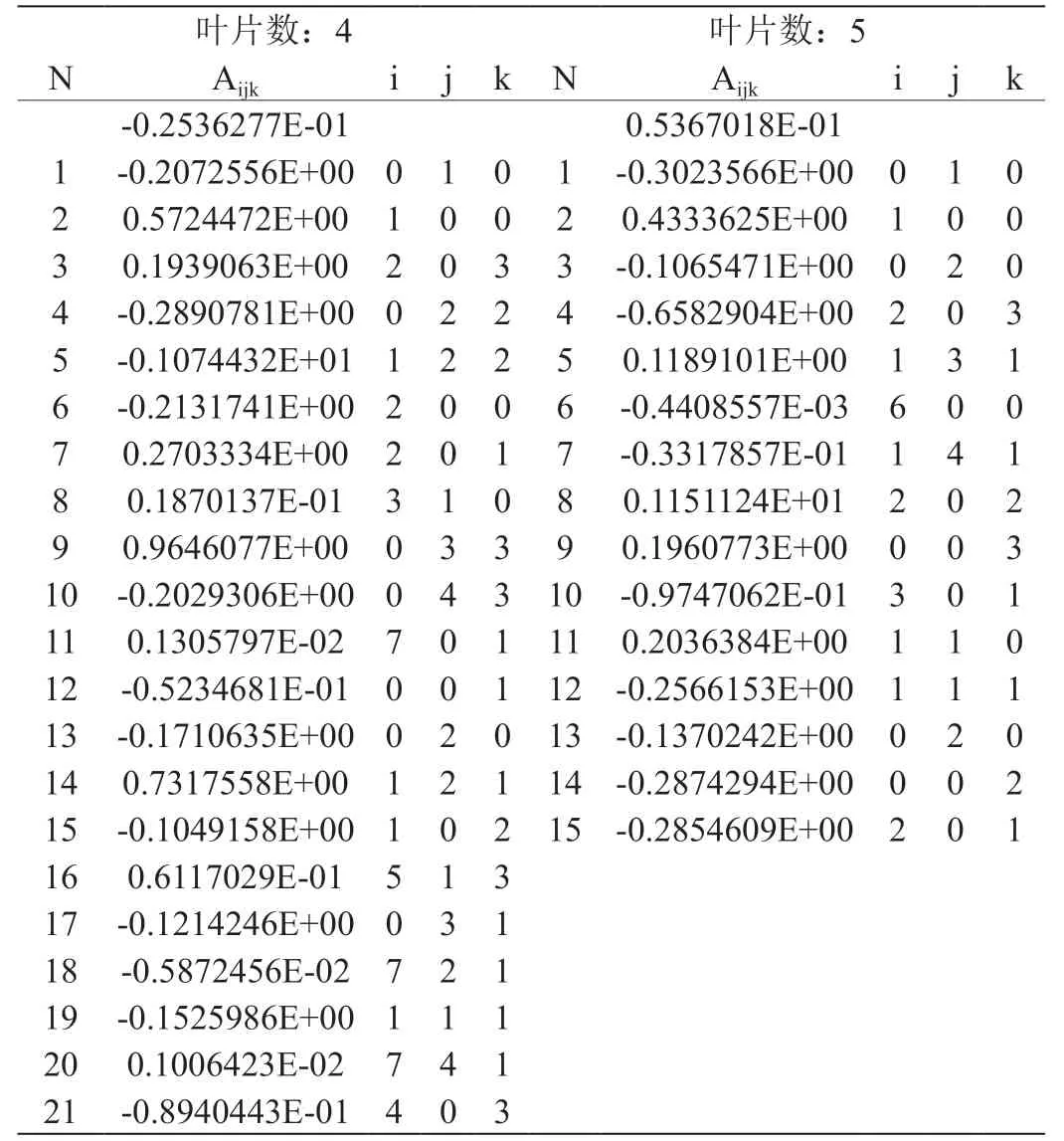
表2：AU 系列螺旋槳回歸公式系數與指數

伴流分數ω 與推力減額分數t 均有多種公開的近似公式，這里分別采用適用于各種海船計算的泰勒公式[4]計算ω，桑海公式[4]計算t。

單槳船：

k=0.5~0.7（流線型舵或反應舵）、k=0.7~0.9（方形舵柱的雙板舵）、k=0.9~1.05（單板舵）雙槳船：

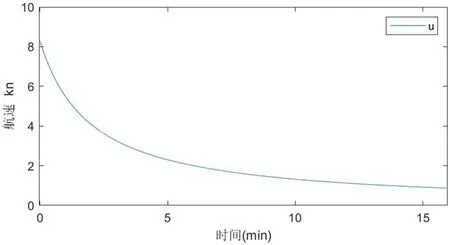
圖2：計算工況1 航速曲線

圖3：計算工況1 位移曲線

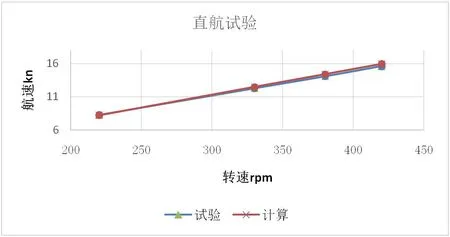
圖4：直航試驗計算與試驗航速對比

3 基于系列圖譜的推力系數計算

3.1 B系列螺旋槳回歸公式

B 系列螺旋槳的敞水性能曲線按進速系數J、螺距比P/D、盤面比AE/AO、槳葉數Z 進行回歸分析，當雷諾數Rn=2×106時表達式為[4]：

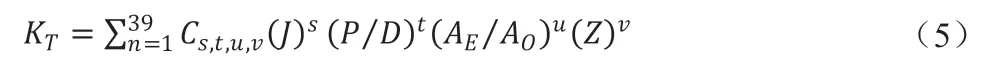
式中各項系數與指數見表1。

當雷諾數Rn>2×106，按照下式對在Rn=2×106的KT增加Δ KT進行修正：

表4：某型船舶主要參數

表5：惰性試驗計算

表6：直航試驗計算

3.2 AU系列螺旋槳回歸公式

AU 系列螺旋槳敞水性能曲線按不同葉片數分別進行回歸精確度較高，其回歸多項式表達如下[4]：

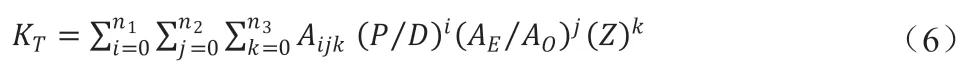
不同葉片數的回歸系數見表2。

3.3 高恩系列螺旋槳回歸公式

高恩系列螺旋槳回歸公式同B 系列，其各項系數與指數見表3。

4 計算案例

采用基于系列圖譜回歸公式的方法對某型船舶進行數值計算，與實船試驗結果對比，以驗證該方法的可行性。該船部分主要參數與試驗數據見表4。

對該船進行惰性計算，與試驗數據對比結果見表5 及圖2~4。

從惰性試驗計算結果來看，該船的水動力計算精度較高，可為螺旋槳計算結果的檢驗做鋪墊。

進一步對該船進行直航試驗計算，采用高恩系列螺旋槳回歸公式計算螺旋槳推力，結果見表6 與圖4。

可見采用螺旋槳回歸公式在船舶直航試驗計算中取得較高的計算精度，在缺少四象限螺旋槳敞水試驗數據時采用該方法進行船舶運動數學模型的計算十分方便。

5 總結

對B 型槳、AU 系列槳、高恩系列槳采用基于系列圖譜的回歸公式計算船舶螺旋槳推力，對缺少螺旋槳敞水試驗數據的船舶而言，該方法具有計算精度高、計算簡便等優點，但由于已知圖譜數據僅針對螺旋槳正車試驗數據，因此采用該方法具有一定局限性，可根據使用目的在船舶駕駛模擬器、船舶自動控制等需要對船舶運動數學建模計算的研究內容得到一定應用。