水平循環立體車庫吊籃運動不干涉條件分析及優化設計

楊劍堯 肖志權 楊政宇

武漢紡織大學機械工程與自動化學院 武漢 430200

0 引言

我國機動車保有量的迅速增加帶來停車困難等問題，在城市繁華地段、寫字樓、賓館、大廈、商場、住宅小區、旅游景點等地點顯得尤為明顯[1]。截至2019年6月,全國汽車保有量達2.5億輛,私家車達1.98億輛[2]。而現有的停車設施多為簡易的平面式停車場，占用了大量土地資源，不能和迅速增長的汽車數量相匹配，造成目前停車位嚴重缺乏的局面[3]。為了緩解停車難的問題，停車樓、升降橫移類、簡易升降類、垂直循環類、水平循環類停車設備相繼提出。就目前機械停車設備市場而言，占用率最高的為升降橫移類（75%），其空間利用率比地面式停車場有較大提高，但其利用率還不到2%。根據停車位設計要求，升降橫移類空間高度不小于3.6 m，高度不夠的地下停車庫則不能安裝。對比升降橫移類，水平循環類空間利用率可提升為2.23%，且省去額外車輛橫移升降通道及相關機械裝置，有效提高車位容量[4,5]。水平循環類停車設備構造簡單、制造成本降低、高效低耗、性價比高、對場地的適應性更強，該種停車庫能很好地解決停車難的問題，有較高經濟價值和社會效益。

1 工作原理

水平循環類立體車庫的運行特點是采用一個水平循環運動的車位系統存取車輛，最適宜建于地形狹長的場所[6]。目前有兩種形式的水平循環類停車庫，即方形循環式和吊籃式。其中，方形循環式立體車庫以方形運動的方式上下層車位交換，在停車系統中兩頭各設置1臺驅動電機，可以是二層或多層。吊籃式立體車庫是以圓形運動方式實現不同層位車位封閉環式的循環交換，停車系統只需設置1臺驅動電機，一般適合二層。

吊籃式立體車庫采用水平循環鏈運動方式移動載車吊籃實現車的存取，載車吊籃循環運動示意如圖1所示（12車位吊籃式停車設備）。在牽引構件鏈條上，每隔一定距離安裝一個載車吊籃，通過電機的減速轉動帶動傳動機構[7]。在循環運動過程中，載車吊籃也將隨著鏈條做循環運動，通過人機界面與PLC實現簡單便捷的人機交互操作，控制驅動電機的正反轉，從而控制載車吊籃的循環運動，實現簡單方便的自動控制，從而達到存取車輛的目的。

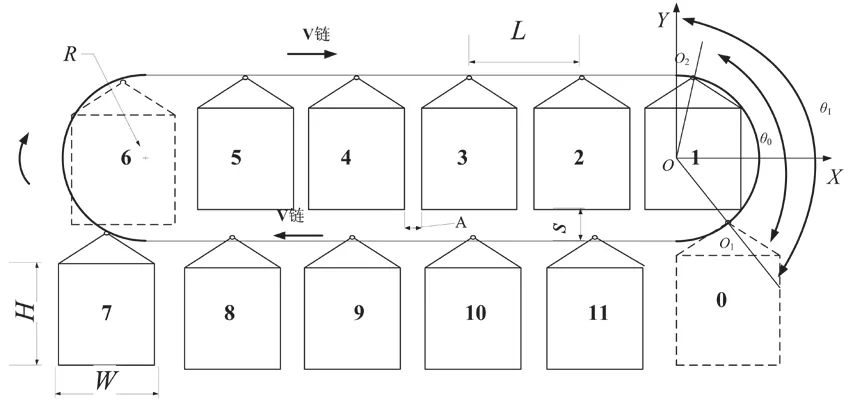
圖1 載車吊籃循環運動示意圖

2 吊籃運動不干涉條件研究意義

載車吊籃做循環運動時，考慮到各吊籃之間的緊湊性，在保證空間利用率高的同時也要保證各個吊籃之間不會發生干涉，使車庫正常運行。若將相鄰吊籃之間距離縮小，提高了空間利用率，但在圓弧部分相鄰兩吊籃會發生干涉現象（見圖1），反之可避免干涉，但空間利用率會降低，車庫的制造成本也隨之增加。吊籃的設計不僅關系車輛存放的安全，還影響到整個車庫裝置的運行安全，故吊籃運動不干涉條件的合理設計對整個車庫裝置有很重要的影響。

如圖1所示，吊籃隨著鏈條做循環運動，由于吊籃在進入圓弧部分時，水平運動速度將小于鏈條的運動速度，針對吊籃在圓弧部分做旋轉運動時不發生干涉，且相鄰吊籃之間的間距不宜過大的問題；通過對吊籃循環運動時的特性進行仿真，分析影響吊籃在圓弧部分運動時發生干涉現象的條件，并進行優化設計。

3 吊籃運動不干涉條件分析

吊籃在進入圓弧部分運動時，吊籃運動的特性分為4個階段，對各個階段干涉條件進行分析，并通過運動仿真及優化設計，得到合理的優化方案。為便于分析，考慮將吊籃實際的外形輪廓進行簡化，將吊籃軸測圖輪廓簡化成矩形（見圖2）。由于簡化的吊籃外形輪廓已將原有外形輪廓包括，故簡化后的運動規律也適用于原有的吊籃外形。

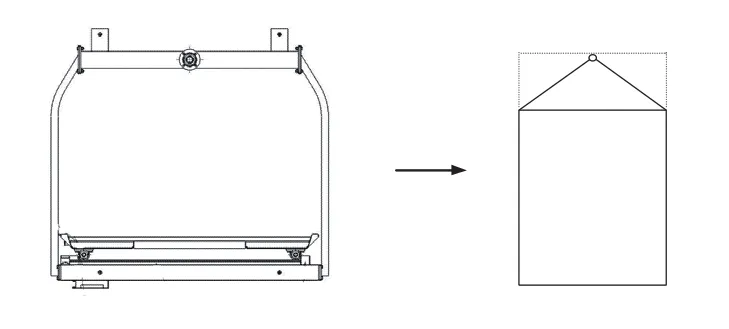
圖2 吊籃軸測圖輪廓簡化圖

3.1 吊籃運動4個階段過程概述

通過建立參考坐標系，對吊籃0、吊籃1的4種運動位置狀態進行分析（見圖1），第一階段O1沿著半徑為的圓弧運動，O2保持水平向右運動，直至O2到達（0，R）點后進入第二階段，O1、O2沿著同一圓弧運動（此時吊籃0比吊籃1更加靠右），第三階段O1、O2沿著同一圓弧運動（此時吊籃1比吊籃0更加靠右），第四階段O2沿著半徑為的圓弧運動，O1保持水平向左水平運動。

3.2 優化設計過程

為了使兩個相鄰吊籃在運動過程中不發生干涉現象，對吊籃運動過程中的相關參數進行假設定義，設兩相鄰吊籃的上邊中心O1、O2水平方向的距離為ΔX，垂直方向的距離為ΔY，要求當O1、O2之間的水平距離ΔX小于載車吊籃的寬度W時，其垂直方向的距離ΔY大于載車吊籃的高度H，即若0≤ΔX≤W時，∣ΔY|＞H，此時兩個相鄰吊籃就不會發生干涉現象。通過選擇合適的傳動系統鏈輪節圓半徑R以及鏈輪齒數Z就能使吊籃之間避免發生干涉現象，優化設計過程主要由確定設計變量、建立目標函數和確定約束條件3部分組成。

1)確定設計變量

在確定設計變量時，首先確定已知量和代換相關變量，吊籃寬度W、吊籃高度H、水平運動時吊籃垂直方向上間隔的安全距離S、相鄰兩吊籃間隔的安全距離A均為已知量。根據實際情況選擇鏈條節距P，即吊籃水平運動中，中心點O1、O2之間距離L、鏈節數N和相鄰兩吊籃同時運動時OO1于OO2之間的夾角θ0可以代換，其中鏈輪節圓半徑R和吊籃0的鏈板旋轉時，OO1與Y軸夾角θ1不能代換，故列其設計變量，即

鏈節數N代換為

式中：N為鏈節數，故N取整數。

中心點O1、O2之間距離L代換為

根據鏈傳動分度圓計算為

鏈輪齒數Z代換為

相鄰兩吊籃同時運動時OO1于OO2之間的夾角θ0代換為

故設計變量為2個獨立變量節圓半徑R、吊籃0的鏈板旋轉時OO1與Y軸夾角θ1，即

2)目標函數的建立

為了求得最佳鏈輪齒數Z，目標函數可以表達為

3)約束條件的確定

吊籃運動時，垂直方向相鄰兩吊籃之間的垂直距離(H+A)要大于圓弧直徑2R，故

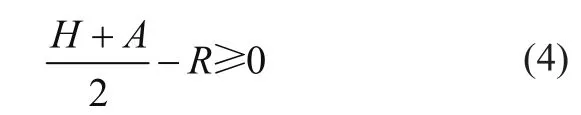
在吊籃鏈傳動設計時，根據經驗對鏈條節距P和齒數Z選擇合適范圍a≤Z≤b，從而對節圓半徑的約束條件為

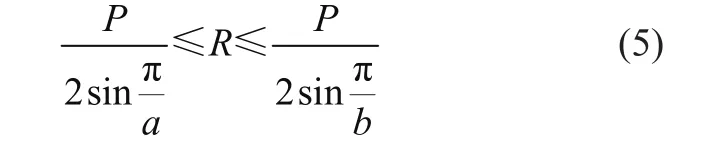
當吊籃進入第一階段時，即O1沿著半徑為R的圓弧運動，O2保持水平向右運動，此時0≤θ1≤θ0，其中，t為吊籃0在旋轉角度時θ1所消耗的時間，ω為鏈輪的旋轉角速度，v為吊籃在水平方向上的移動速度，即

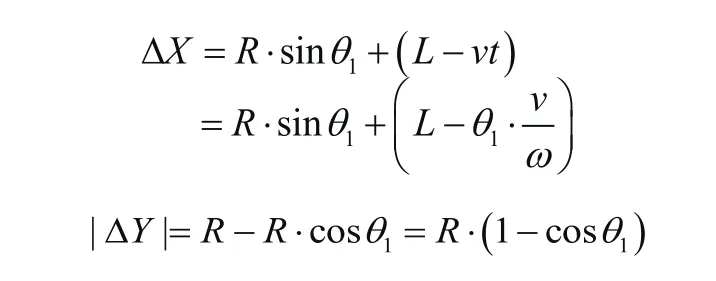
即由吊籃不干涉條件為

當O1、O2的橫坐標相同時為第二階段的結束點，也是進入第三階段的開始點，此時θ1= （ π + θ0）2。故當吊籃進入第二階段時，即O1、O2沿著同一圓弧運動（此時吊籃0比吊籃1更加靠右），此時。即

由吊籃不干涉條件得

當吊籃進入第三階段時，與第二階段相似，O1、O2沿著同一圓弧運動（此時吊籃1比吊籃0更加靠右），此時。即

即由吊籃不干涉條件得

當吊籃進入第四階段時，此時O2沿著半徑為R的圓弧運動，O1保持水平向左水平運動，由于吊籃可以環形正反兩個方向運動，所以第四階段可看作是第一階段的逆向運動，故第一階段的運動規律適用于第四階段。

由上述條件可對約束條件進行確定，即由式(4)得垂直方向相鄰兩吊籃之間距離約束函數為

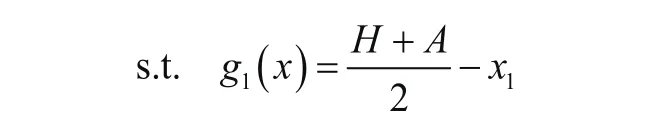
由式(5)得節圓半徑約束函數為

由式(6)得第一階段相鄰吊籃運動不干涉約束函數，即當0≤x2≤θ0時

由式(7)得第二階段相鄰吊籃運動不干涉約束函數，即當 θ0≤ x2≤（π+θ0）/2 時

由式(8)得第三階相鄰吊籃運動不干涉段約束函數，即當（π + θ0）2≤x2≤π 時

第四階段相鄰吊籃運動不干涉約束函數與第一階段相同。吊籃0的鏈板旋轉時OO1與Y軸夾角θ1在運動時角度變化范圍為0～π，即

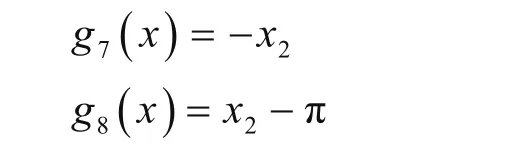
3.3 優化求解

利用Matlab優化工具箱對數學模型進行求解，假設已知W=2 500 mm，H=2 300 mm，S=500 mm，A=150 mm，P=460 mm，Z取10～30。其Matlab最優解主程序為

綜上所述，運用優化設計方案以及數學模型，對假設實例求解，求得最優結果Z=19，滿足實例吊籃運動不干涉條件以及立體車庫空間利用率要求，為類似水平循環車庫的結構設計提供方法參考。

4 結語

本文結合我國機動車保有量發展情況以及市場機械式立體車庫使用率，通過與采用率最高的升降橫移類停車設備對比，選擇對場地適應性更強、空間利用率更高的水平循環類停車設備進行研究分析。針對水平循環吊籃式立體車庫吊籃運動不干涉條件，通過對吊籃運動特性仿真分析，并對假設實例優化求解，給出合理的計算方法，為水平循環吊籃式立體車庫結構設計以及傳動系統的設計提供合理參考。