基于共享內存的過約束多自由度振動臺解耦控制方法

李寧　陳俊　高樹靈　韓慶華　李忠獻

摘要： 為了提高由過約束作動器驅動的地震模擬振動臺振動信號的復現性能，對振動臺和控制系統進行建模和小尺寸模型振動臺試驗驗證，分析了采用8個作動器耦聯驅動的小型三向六自由度振動臺系統特性，在理論上采用正、反運動學模型對其進行動態解耦;利用混合試驗中的共享內存具有的實時存儲與讀取的功能，以控制器、SpeedGoat及數據采集系統構建去中心化的控制系統硬件平臺，采用SpeedGoat旁路控制器，對所提出的解耦控制方法進行了試驗驗證，證明了該控制方法的可行性和可靠性。經試驗驗證的機構解耦算法運算量小，可拓展多種更復雜的控制方法，在硬件平臺更普適。

關鍵詞： 振動臺; 三向六自由度; 解耦控制算法; 共享內存; Simulink

中圖分類號： TB534+.2; TP242 ? ?文獻標志碼： A ? ?文章編號： 1004-4523（2021）02-0329-09

DOI：10.16385/j.cnki.issn.1004-4523.2021.02.013

引 言

并聯驅動與傳統串聯驅動構造的機械體系相比，具有剛度大、精度高、動力性能好以及承載能力高等優點。振動臺是工業振動檢測、結構抗震等研究的重要試驗設備，已經被廣泛地應用在航空航天、車輛交通、建筑結構和工業自動化等眾多工程領域[1]。多自由度振動臺由并、串聯系統構成，其運動學和動力學分析可能存在不同程度的耦合，進行解耦控制方法的研究十分必要。

對于并聯機構，運動學解答往往需要進行迭代求解。1992年，Zhang等[2]就提出了一種簡單方法計算運動學正向解答，此后國內外學者在此基礎上做了許多研究。Koekebakker[3]對Stewart平臺進行詳盡的運動學與動力學分析，提出了一種基于模型的控制器設計方法。McInroy等[4?5]提出了兩種解耦算法。Chen等[6]和Yang等[7]在此基礎上，提出一種將一個高度耦合的六輸入六輸出的動力學系統轉化成六個獨立的液壓驅動機械系統的新控制方法，并證明其可行性。Yang等[8]與Peter等[9]將多輸入多輸出（MIMO）系統轉換到多個單輸入單輸出（SISO）系統進行控制，驗證了模態解耦控制的有效性。Plummer等[10]則基于模態空間控制思想，通過模態矩陣轉換將關節空間坐標的單缸控制轉換到無耦合空間，并對6?6 Gough?Stewart平臺進行建模仿真。在實際的控制器設計中，由于六自由度運動系統硬件性能難以保證，盡管模態解耦的思想理論上能取得一定效果，但實際上可能成本過高，Chen等[6]和Plummer等[10]所使用高性能六自由度運動系統硬件成本可觀。因此，合理地建立機構的運動學和動力學模型、優化控制方法、挖掘系統潛力是有必要的。

濱海土木工程結構與安全教育部重點實驗室（天津大學）自行研制的750 mm×750 mm電動地震模擬振動臺，滿負載為300 kg，可實現三向六自由度激振。本文對該振動臺的部件組成進行了介紹，對笛卡爾坐標系和作動器過約束坐標系下的自由度轉換和解耦控制算法進行了推導，編制相關控制程序并實現了基于反射內存和Simulink的控制平臺搭建，最后進行了試驗驗證，為后期進行更優質的控制系統研究及相關試驗奠定基礎。

1 電動振動臺組成

振動臺采用8套完全相同的電動作動器及驅動器來實現加載臺面的六自由度運動。4支垂直向作動器和4支水平作動器如圖1所示。需要說明的是，考慮到實驗室無條件構造反力地基/臺架，設計了自平衡振動臺構型，其水平向作動器呈45°角V形布置，4個豎向作動器豎向布置;此外，其協同工作中心在臺面高于水平、豎向作動器，使得臺面處水平向、豎向作動器球鉸并不共點、共線。平衡時各作動器空間坐標如表1所示（假設臺面中心位置為原點），作動器空間幾何模型如圖2所示。采用FlexTest 60實時控制器（配備MTS 793軟件平臺），配置控制器硬件接口文件，將列出的系統資源池中定義資源匹配給各物理通道，即可創建多功能的站臺配置文件。使用臺站生成器窗口控件以分配硬件資源，如閥驅動、反饋通道、模擬I/O、數字I/O等資源。

1.1 機械部分組成

機械部分包括運動臺面、反力框架、電機與球鉸4個部分。其中運動臺面及反力框架采用鋁合金材料制作。電動作動器和電機（如圖3所示）分別采用美國Parker公司生產的ETH系列作動器和PM系列電機。電機最高轉速5000 r/min、最高電流7.8 A，額定扭矩及額定輸出功率分別為1.27 N·m及400 W。電機與絲杠采用并聯式安裝，內置抱閘系統，可通過抱閘控制確保振動臺運作的安全性。該電動作動器的特點是具有一個大尺寸的汽缸桿，而螺桿螺母軸承采用優質塑料滑動軸套形式，以吸收側向力。因為振動臺需要具有較長行程，電動缸會有較高的側向力，為了增加容許的側向力，選擇了比實際應用要求更長的行程。

1.2 電氣部分組成

自行設計了電氣控制柜，包括驅動器（如圖4所示）、傳感器、接線組和線纜四個部分。伺服驅動器模擬輸入具有兩通道，可分別控制轉速和扭矩，電壓限制為±10 V、模擬輸出二通道（±10 V），可自定義輸出任何內部參數。傳感器由24套限位開關（每缸3支）及8套編碼器組成。增量型編碼器可輸出24 V邏輯差分ABZ信號。控制柜總體組成如圖4所示。圖4中1?9分別為總電源空氣開關、急停斷路器、各驅動器供電開關、電源濾波器、24 V電源、驅動器IO接線端、驅動器、電池盒以及臨時接線板。

2 耦聯多自由度系統控制原理

采用8支作動器控制振動臺臺面運動具備六自由度，作動器只能按照指令沿其軸線方向移動，通過8個作動器的軸線運動實現六自由度的加載運動，需要作動器和笛卡爾空間坐標之間的運動轉換。因為各自由度之間存在運動機構的耦合關系，所以需要對其進行運動學分析。圖5描述了并聯笛卡爾坐標系統，并聯機構（如圖5（a）所示）由n個移動關節（即作動器或位移傳感器）組成。第“i”關節一端與A點的固定物體連接，另一端與B點的運動物體連接，n個關節與兩個物體平行連接。可在每個主體上定義兩個坐標框架系統：一個附著在基座上的“固定”框架，另一個附著在加載平臺上的“運動”框架，如圖5（b）所示。

3 振動臺控制系統設計

在振動臺系統中，為實現閉環控制，需要基于反饋概念以減少不確定性。PID控制器是在工業實際中應用最廣泛的一種控制器。

3.1 PID控制器

PID控制是由比例部分（Proportional）、積分部分（Integral）和微分部分（Derivative）組成的一種線性調節器。PID控制器把實際輸出信號y（t）與輸入信號r（t）的值進行比較，然后將誤差e（t）用于計算得出新的輸出信號u（t），使系統的輸出能夠有效追蹤參考信號，如圖7所示。

在時域的PID控制規律可以寫成

u（t）=K_P [e（t）+1/T_i ?∫_0^t?〖e（t）dt+T_d ?（de（t））/dt〗] ? （12）

式中 e（t）=r（t）-y（t）為PID控制器的輸入，K_P為比例系數、T_i為積分時間常數、T_d為微分時間常數。將式（12）經過拉式變換，得到

G（s）=（U（s））/（E（s））=K_P （1+1/（T_i s）+T_d s） （13）

其中，通過調節K_P能迅速減小偏差，但不能消除穩態誤差，K_P過大還會引起系統不穩定;為了消除穩態誤差，引入“積分項”，積分控制器能在系統中加入一個位于原點的極點，以消除輸入及外部干擾，使系統進入穩態后能消除穩態誤差。但引入極點會使系統變得較不穩定，因此引入微分控制器，在系統中增加一個零點以維持穩定[18?19]。本文中，對搭建的軟硬件平臺能否實現較為精準的控制效果，探討其可靠性與可行性。建議P，I和D值分別調制為8.5，2和0。

3.2 硬件及軟件組成

3.2.1 控制器硬件平臺

FlexTest 60實時控制器通常用于液壓伺服試驗系統。可提供實時閉環控制、傳感器標定和函數生成等，以驅動各種類型的作動器。本文使用FlexTest 60具有8個AO控制通道和8個編碼器反饋通道，可對振動臺的8個作動器進行控制。此外也可配置冗余的傳感器輸入通道記錄位移、加速度、力等的需求。控制器配備了電動作動器控制包，在Windows操作系統下，可以進行多任務處理[20?21]。試驗時，可根據試驗事件調整控制參數。系統軟件包中包含有輔助應用程序，它們可用于執行特定的開機、保持、停機等試驗過程的序列伺服控制動作。

3.2.2 共享內存平臺

實時子結構實驗中需要求解運動方程，并作為目標位移采用作動器實現。目前通常試驗采用控制器來代替計算機進行目標位移的計算，控制器再通過AD/DA轉換來與傳感器及伺服系統相連，以構成一個完整的實時子結構實驗系統[22?23]。本文配置了共享內存設備用于上位機與控制器的實時通信。此外，為了實現上述解耦控制的LFKT算法，編制了Simulink控制程序（包括PID，IKT和LFKT），利用SpeedGoat與FlexTest 60控制器數據實時交互。此時，Flex Test 60控制器的編碼器反饋位移和AO的驅動命令構成閉環，與SpeedGoat中運行的Simulink對接進行控制。

3.2.3 調試平臺

Simulink便于對動態系統建模、仿真和分析，能對系統的所有部件協同工作進行仿真。SpeedGoat半實物仿真與測試平臺是由瑞士SpeedGoat公司開發的一套基于Simulink的硬件在環（HIL）仿真與測試平臺。本文采用Matlab/Simulink結合進行實時測試，利用SpeedGoat完成基于模型的模擬設計、仿真及驗證工作等。SpeedGoat與Simulink協同工作，便于提高HIL系統開發的效率，該平臺可適應線性、非線性系統，連續、離散及混合系統開發，SISO及MIMO系統的仿真等，具備很強的拓展能力。

3.3 多自由度解耦控制平臺搭建

基于第2節闡述的理論，利用Simulink對研發的電動振動臺進行數學建模，通過SpeedGoat運行解耦控制結果，用反射內存與FlexTest控制器實時數據交互，FlexTest對振動臺每個作動器發出預設指令，采集反饋位移。圖8?9為FKT與IKT的Simulink框架圖，是基于式（1）?（9）所述運動學變換理論所構建的。進行相應的多自由度解耦計算，其中LFKT內嵌于正運動學變換中。通過解耦運算，可減小各作動器之間的耦合，使控制更為精準。

在此控制平臺中，SpeedGoat執行多自由度解耦計算模型，共享內存模塊通過實時連接，將計算指令下載至共享內存中并與控制器進行數據交換，控制器將共享內存中的指令數據下載并發給FlexTest60控制器，驅動作動器。FlexTest的輸出范圍可根據驅動機構要求設置為±10 V。在濱海土木工程結構與安全教育部重點實驗室（天津大學），進行了實時仿真運行。該平臺用數字信號連接了多個試驗系統架構中的位移命令發送模塊及數據采集系統模塊，最大幅度地減少了噪聲的引入，控制平臺總體架構如圖10所示。

完成試驗后，搭載Simulink的上位PC機可以通過模塊記錄控制指令與反饋指令，之后便可在Matlab命令框中調用數據，方便進行數據的處理。

4 控制系統效果測試

為實時對比觀察控制效果，首先可借助Parker公司的軟件Drive Support Tool對電機工作參數進行觀測調整（如圖11所示）。通過軟件觀測各作動器的實際位移值并將其輸入FlexTest控制器中，使控制器中記錄的每個作動器的位移值與實際值一致，檢查好線路后即可開始進行測試。圖12為試驗現場照片。

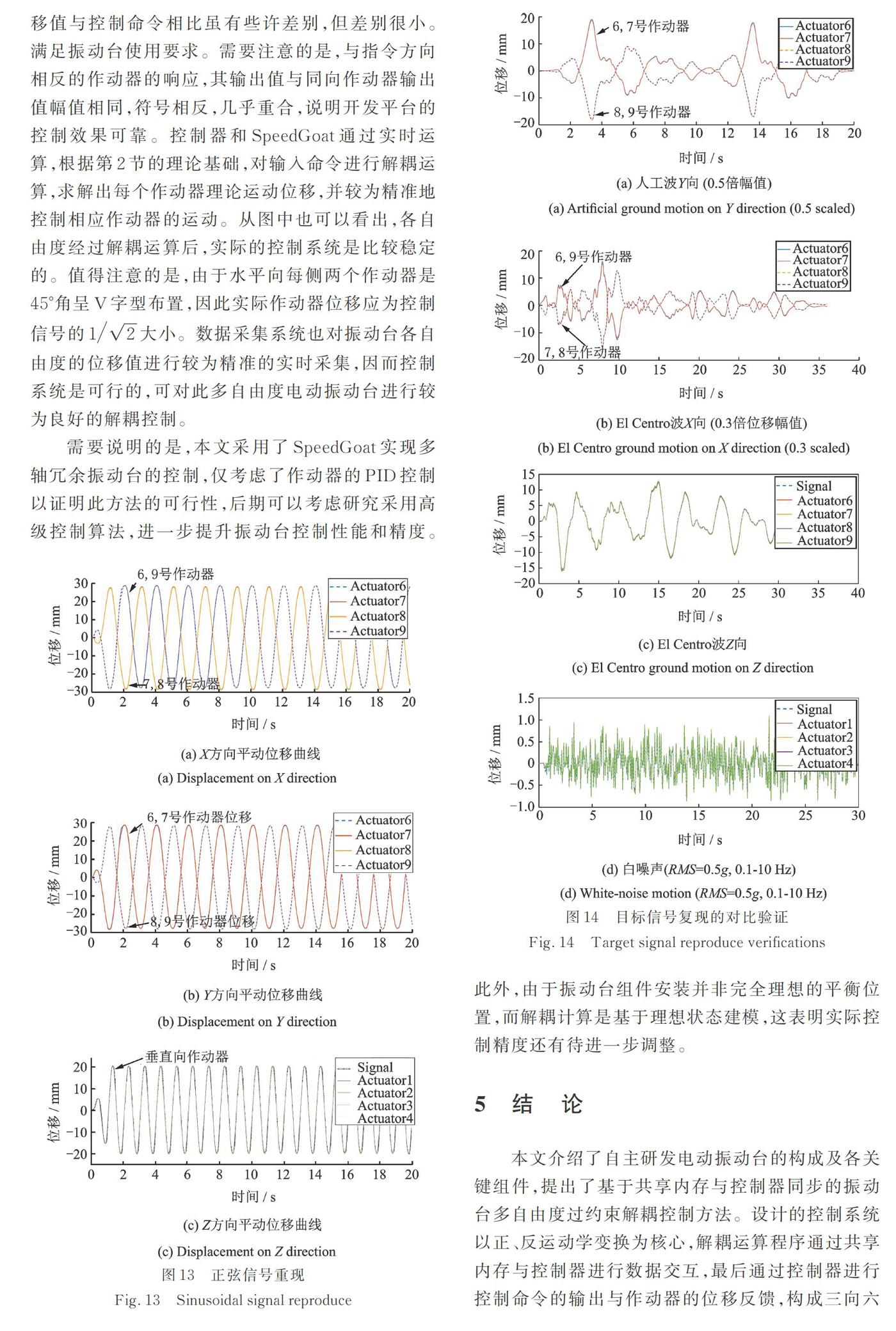
為驗證控制系統可靠性，對系統進行相應的測試。測試包括周期、地震動和白噪聲測試。周期正弦波測試工況如表2?3所示。需說明的是，所有測試至少重復兩次以進行可靠性比對。控制信號及反饋信號對比如圖13?14所示。

由圖13?14可以看出，各種工況下實際輸出位移值與控制命令相比雖有些許差別，但差別很小。滿足振動臺使用要求。需要注意的是，與指令方向相反的作動器的響應，其輸出值與同向作動器輸出值幅值相同，符號相反，幾乎重合，說明開發平臺的控制效果可靠。控制器和SpeedGoat通過實時運算，根據第2節的理論基礎，對輸入命令進行解耦運算，求解出每個作動器理論運動位移，并較為精準地控制相應作動器的運動。從圖中也可以看出，各自由度經過解耦運算后，實際的控制系統是比較穩定的。值得注意的是，由于水平向每側兩個作動器是45°角呈V字型布置，因此實際作動器位移應為控制信號的1?√2大小。數據采集系統也對振動臺各自由度的位移值進行較為精準的實時采集，因而控制系統是可行的，可對此多自由度電動振動臺進行較為良好的解耦控制。

需要說明的是，本文采用了SpeedGoat實現多軸冗余振動臺的控制，僅考慮了作動器的PID控制以證明此方法的可行性，后期可以考慮研究采用高級控制算法，進一步提升振動臺控制性能和精度。此外，由于振動臺組件安裝并非完全理想的平衡位置，而解耦計算是基于理想狀態建模，這表明實際控制精度還有待進一步調整。

5 結 論

本文介紹了自主研發電動振動臺的構成及各關鍵組件，提出了基于共享內存與控制器同步的振動臺多自由度過約束解耦控制方法。設計的控制系統以正、反運動學變換為核心，解耦運算程序通過共享內存與控制器進行數據交互，最后通過控制器進行控制命令的輸出與作動器的位移反饋，構成三向六自由度振動臺反饋控制。

試驗結果表明，所研發控制方法具有較好的跟蹤性能，通過模擬模型可事先進行預期的振動臺運動效果分析、用于系統的離線調試等，避免在線調試中的困難。相關控制算法達到了預期的控制效果，驗證了研發的控制平臺的可行性和可靠性。

參考文獻：

[1] 高春華，紀金豹，閆維明，等. 地震模擬振動臺技術在中國的發展[J]. 土木工程學報，2014，47（8）：9-19.

Gao Chunhua， Ji Jinbao， Yan Weiming， et al. Developments of shaking table technology in China[J]. China Civil Engineering Journal， 2014， 47（8）： 9-19.

[2] Zhang Chang-de， Song Shin-Min. Forward position analysis of nearly general Stewart platforms[C].ASME 22nd Biennial Conference on Robotics，Spatial Mechanisms， and Mechanical Systems，Scottsdale，USA，1992： 81-84.

[3] Koekebakker S H. Modal based control of a flight simulator motion system[D]. Delft： Delft University of Technology， 2001.

[4] McInroy J E. Dynamic modeling and decoupling force control of a precision hexapod[J]. IFAC Proceedings Volumes， 1998，31（27）： 231-236.

[5] McInroy J E， Hamann J C. Design and control of flexure jointed hexapods[J]. IEEE Transactions on Robotics and Automation， 2000 ，16（4）： 372-381.

[6] Chen Yixin， McInroy J E. Decoupled control of flexure-jointed hexapods using estimated joint-space mass-inertia matrix[J]. IEEE Transactions on Control Systems Technology，2004， 12（3）： 413-421.

[7] Yang Chifu， Huang Qitao， Han Junwei. Decoupling control for spatial six-degree-of-freedom electro-hydraulic parallel robot[J]. Robotics and Computer-Integrated Manufacturing， 2012， 28（1）： 14-23.

[8] Yang Chifu， Han Junwei. Dynamic coupling analysis of a spatial 6-DOF electro-hydraulic parallel manipulator using a modal decoupling method[J]. International Journal of Advanced Robotic Systems， 2013， 10（2）： DOI：10.5772/55028.

[9] Peter O Ogbobe， Ye Zhenmao， Jiang Hongzhou， et al. Modal space decoupled controller for hydraulically driven six degree of freedom parallel robot[C]. 2nd International Conference on Mechanical and Electronics Engineering， Kyoto， Japan， 2010： Vl-280-Vl-284.

[10] Plummer A R， Guinzio P S. Modal control of an electro hydrostatic flight simulator motion system[C]. ASME Dynamic Systems and Control Conference， Hollywood，USA， 2009.

[11] 魏巍. 冗余多軸振動臺耦合特性分析及其控制策略研究[D]. 哈爾濱：哈爾濱工業大學，2017.

Wei Wei. Coupling analysis and its control strategy of redundant multi-axis shaking table[D]. Harbin： Harbin Institute of Technology， 2017.

[12] 齊玙珂. 六自由度運動系統的模態空間解耦控制器的適用性研究[D]. 哈爾濱：哈爾濱工業大學，2012.

Qi Yuke. Study on applicability of modal space decoupled controller for a hydraulically driven stewart platform[D]. Harbin： Harbin Institute of Technology， 2012.

[13] 陳宥全. 多自由度振動臺之主動即時控制系統開發與應用[D]. 新竹：國立清華大學，2012.

Chen Y C. Development and application of active real-time system for the control of multi-degree-of freedom shaking table[D]. Hsinchu： National Tsing Hua University， 2012.

[14] 樊 強. 多軸冗余振動臺的模態與自由度復合控制[D]. 哈爾濱：哈爾濱工業大學，2017.

Fan Qiang. Combination of modal and degree control strategy study of redundant multi-axis shaking table[D]. Harbin： Harbin Institute of Technology， 2017.

[15] Zhou Huimeng， Li Mengning， Wang Tao. Force-displacement decoupled control of engineering structures with multi degree-of-freedom testing[C]. 14th International Symposium on Structural Engineering， Beijing， China， 2016： 855-862.

[16] Fermandois G A， Spencer B F. Model-based framework for multi-axial real-time hybrid simulation testing [J]. Earthquake Engineering and Engineering Vibration， 2017， 16（4）： 671-691.

[17] Mercan O， Ricles J M， Sause R， et al. Kinematic transformations for planar multi-directional pseudodynamic testing[J]. Earthquake Engineering and Structural Dynamics， 2009， 38（9）： 1093-1119.

[18] 胡世強. 基于先進PID算法的振動臺控制仿真和模型共振研究[D]. 哈爾濱：哈爾濱工業大學，2011.

Hu Shiqiang. Research on control system of shaking table based on two advanced PID and analysis on coupled model and table[D].Harbin： Harbin Institute of Technology， 2011.

[19] 舒懷林. PID神經元網絡多變量控制系統分析[J]. 自動化學報，1999，25（1）： 105-111.

Shu Huailin. Analysis of PID neutral network multivariable control systems[J]. Acta Automatica Sinica，1999， 25（1）： 105-111.

[20] MTS Systems Corporation MTS. Series 793 Controller Overview [M]. Eden Prairie，MN 55344， USA， 2011.

[21] MTS System Corporation MTS. Series 793 Hybrid Simulation： User Information and Software Reference [M]. Eden Praire，MN 55344， USA， 2013.

[22] 陳永盛，吳 斌，王 貞，等. 基于Simulink 的混合試驗系統及其驗證[J]. 振動與沖擊，2014，33（7）：18-23.

Chen Yongsheng， Wu Bin， Wang Zhen， et al. Simulation and validation of a hybrid testing system with Simulink [J]. Journal of Vibration and Shock， 2014， 33（7）： 18-23.

[23] 許國山，吳 斌. 采用比例-積分控制的實時子結構試驗等效力控制方法[J]. 工程力學，2009，26（9）：251-256.

Xu Guoshan， Wu Bin. Equivalent force control method with proportional-integral controller for real-time substructure testing [J]. Engineering Mechanics， 2009， 26（9）： 251-256 .

Reflective memory based over-constraint MDOF decouple control algorithm for the shaking table control

LI Ning1，2，3， CHEN Jun1， GAO Shu-ling1， HAN Qing-hua1，2，3， LI Zhong-xian1，2，3

（1. School of Civil Engineering， Tianjin University， Tianjin 300350， China; 2. Key Laboratory of Coastal Civil Engineering Structure and Safety， Ministry of Education （Tianjin Univerisity）， Tianjin 300072， China; 3. Key Laboratory of Comprehensive Seismic Engineering Simulation and Urban-Rural Seismic Toughness， China Seismological Bureau， Tianjin University，

Tianjin 300350， China）

Abstract： To improve the reproducing performance of the earthquake records using the shaking table facility with over constraints of multiple actuators， the kinetic model and the control system of the shaking table are established. Based on the small scaled shaking table test， the verification and validation of a three dimensional six degrees of freedom shaking table system driven by eight actuators are performed， where positive and inverse kinematics transformation algorithms is adopted for dynamic decoupling in theory. Based on the nearly real-time storage and reading capacity of the reflex shared memory card， the hardware platform composed with the decentralized control system is constructed using the real-time controller， SpeedGoat and data acquisition system. Then， the decoupling control method is tested with the SpeedGoat bypassing the controller， which proved the feasibility and reliability of the proposed control method. It is validated that the decoupling algorithm of this mechanism is fast with small computational cost， and it can be further developed for more complex control method with versatile functions. The hardware platform is more universal and lays the foundation for subsequent shaking table test and control algorithm development.

Key words： shaking table; three dimensional six degrees of freedom; decouple control algorithm; shared memory; Simulink

作者簡介： 李 寧（1981-），男，教授，博士生導師。電話：15022396067;E-mail：neallee@tju.edu.cn