基于OWA算子的公路工程造價估算模型
郭 鑫
(中交第三公路工程局有限公司,北京 101399)
0 引 言
公路工程造價是公路工程建設中的重要內容,在本質上指的就是公路工程建設所需的成本。公路工程造價估算模型是針對公路工程造價進行估算的主要手段,也是決定能否精準的掌控公路工程效益的關鍵影響因素,并估算出公路工程在未來的收益水平,常用于工程招投標[1]。在針對公路工程造價估算模型的研究中,我國學者邵良杉提出了工程造價人工神經網絡估算模型,通過提出應用神經網絡估算工程造價,根據輸入層考慮主材價格,可以使造價更符合實際。外國學者研究表明80%的項目成本取決于20%的主要工項。因此,利用20%主要工項的造價,可以回推出工程之總造價。雖然利用前者設計的公路工程造價估算模型能夠取得一定程度上的應用效果,但在實際應用過程中往往無法取得極其精準的公路工程造價數目。本文在此基礎上,將OWA算子引入公路工程造價估算模型設計中。OWA算子的亮點在于能夠集結最大與最小算子之間的有效信息,進而提高信息權重計算的精準度,能夠很好地適用于工程造價估算方面。為此,本文提出基于OWA算子的公路工程造價估算模型設計。
1 OWA算子
OWA算子又稱有序加權平均算子,由Yager首次提出,其本質上是一種信息集結方法,主要適用于數據挖掘以及決策理論方面[2]。OWA算子中兩個最重要的指標就是orness測度以及最大熵,通過orness測度以及最大熵的精準度量,反映出OWA算子決策者的樂觀程度。因此,將OWA算子應用在公路工程造價估算模型設計中。
2 基于OWA算子的公路工程造價估算模型
2.1 采集公路工程造價數據輸入輸出
在公路工程造價估算過程中,必須預先確定公路工程造價基礎數據,也就是公路工程特征屬性[3]。為最大減少公路工程造價估算偏差,本文依靠公路工程特征屬性,采集公路工程造價數據輸入輸出。公路工程特征屬性見表1。

表1 公路工程特征屬性
結合表1所示,為公路工程特征屬性,以此為公路工程造價估算影響因素,并確定采集數據輸入輸出。采集數據輸入輸出的具體流程為:首先,運用OWA算子中的orness測度計算兩組數據序列的關聯系數,再計算其不同數據序列之間的關聯度。引入分辨系數δ可從客觀上消除偏差過大的采集點數據,避免模型在后續對公路工程造價估算時出現關聯度失真問題[4]。設不同數據序列之間的關聯度為λ,可得公式(1)。
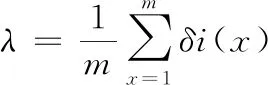
(1)
式中:m為公路工程缺失值;x為公路工程造價估算數據的收斂速度;i為是數據集參數的極大似然估算。為保證本文設計模型在對公路工程造價核心影響因素提取過程中具有客觀性,當0<λ≤0.25時,兩組不同數據序列之間的關聯度為弱關聯;當0.25<λ≤0.75時,兩組不同數據序列之間的關聯度為強關聯[5]。在此基礎上,分析采集數據主成分,將眾多線性相關的影響因素轉換為少數線性不相關的影響因素,切斷在公路工程造價估算過程中相關性的干擾,將高維問題轉換為低維問題,為后續篩選公路工程造價核心影響因素數據提供數據基礎。
2.2 篩選公路工程造價核心影響因素估算數據
本文采用將輸入數據標準化的方法使估算數據落入到[-1,1]范圍內,設公路工程造價核心影響因素估算數據篩選的計算表達式為k,可得公式(2)。
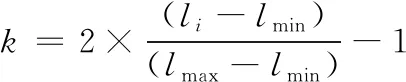
(2)
式(2)中:li為原始輸入數據序列;lmin為有序加權平均算子數據序列最小值;lmax為有序加權平均算子數據序列最大值。將數據篩選后的數據輸入到模型當中,判斷其關聯度,若為弱關聯,則說明該數據所屬的影響因素不屬于核心影響因素將其過濾;若得出的數值為強關聯,則說明該數據所屬的影響因素為核心影響因素,將其篩選出來。
2.3 基于OWA算子計算公路工程造價估算權重
在篩選后得到數據的基礎上,為進一步提高公路工程造價估算精度,基于OWA算子計算公路工程造價估算權重。利用OWA算子中的最大熵指標處理公路工程造價估算數據,設賦權指標為β,可得公式(3)。

(3)
式中:C為公路工程造價極值;z為公路工程預期完成總天數。通過公式(3),得出公路工程造價估算賦權指標,利用公路工程造價估算賦權指標進行基于OWA算子進行加權求和,集結最大與最小算子之間的有效信息,設公路工程造價估算權重計算表達式為ω,可得公式(4)。

(4)
式中:h為公路工程特征屬性的決策參數。通過公式(4),得出公路工程造價估算權重,通過OWA算子,提高公路工程造價估算權重計算的精準度。
2.4 得出公路工程造價估算結果
運用計算得到的公路工程造價估算權重,得到完整的基于OWA算子的公路工程造價估算模型[6]。將公路工程造價估算模型的表達式設為W,以此可得W的計算公式,則有公式(5)。
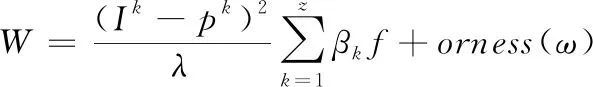
(5)
式中:I為公路工程造價估算的相關字向量;p為公路工程造價估算的相關字維數;f為公路工程造價估算全局極值。通過基于OWA算子的公路工程造價估算模型計算后,可得出公路工程造價估算結果。至此完成基于OWA算子的公路工程造價估算模型設計。
3 實例分析
3.1 實驗準備
選取某公路工程作為實驗對象,設定某公路工程參數信息,包括:工程類型為辦公樓;工程類別屬于一類;工程所用硅供應方式為商品硅;結構類型為框架;地上層數為5層;地下層數為2層。首先使用本文基于OWA算子設計公路工程造價估算模型,估算公路工程造價,記錄估算值;再使用傳統公路工程造價估算模型,估算公路工程造價,同樣記錄估算值。將兩種模型下的估算值與公路工程造價實際值相對比,數值越接近證明該模型的估算精度越高。
3.2 實驗結果及分析
根據上述準備完成對比實驗,得出實驗結果對比表,見表2。
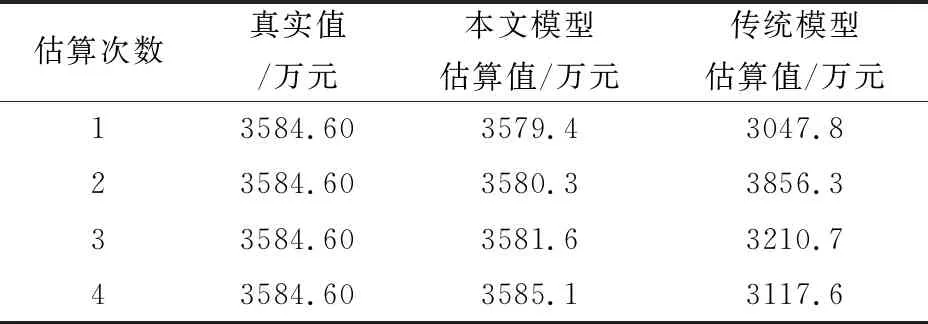
表2 實驗結果對比表
由表2可知,通過本文設計模型得出的工程造價估算值與真實值更接近,證明設計模型的估算精度明顯高于傳統模型,可以實現對公路工程造價的精準估算。
4 結束語
通過基于OWA算子的公路工程造價估算模型設計,能夠取得一定的研究成果,解決傳統公路工程造價估算模型中存在的問題。由此可見,本文設計的估算模型是具有現實意義的,能夠指導公路工程造價估算模型優化。在后期的發展中,應加大本文設計估算模型在公路工程造價估算中的應用力度。截至目前,國內外針對基于OWA算子的公路工程造價估算模型研究仍存在一些問題,在日后的研究中還需要進一步對公路工程造價估算模型的優化設計做出深入研究,為提高公路工程造價估算模型的運行效率提供建議。

