電動汽車電驅動系統機電耦合動態特性研究

葛帥帥，楊雨番，郭 棟，張志剛，易園園

（1.重慶理工大學 車輛工程學院，重慶 400054；2.江漢大學 智能制造學院，武漢 430056）

電驅動系統是電動汽車核心部件之一，其性能直接影響電動汽車的安全與可靠性。電驅動系統主要由電機和齒輪傳動機構組成，是一個典型的機電耦合系統。當電動汽車在變速變載等典型工況下行駛時，會使得機電耦合系統的動力學特性更加復雜，甚至導致傳動系統零部件發生故障失效。因此，考慮電驅動系統機電耦合效應，研究電驅動系統在典型工況下的動態特性，對于保證電動汽車運行安全性及可靠性具有重要理論意義。

近年來，電驅動系統機電耦合特性已成為國內外學者的研究熱點。Bai等［1］考慮電機的磁場分布和傳動系統的時變剛度，建立了機電耦合動力學模型，發現在電機電壓和傳動系統負載發生瞬變時會使機電耦合系統產生劇烈振動。Abraham G等［2］建立了永磁同步電機有限元仿真模型，研究了電極數量和定子槽對電機電磁轉矩波動的影響。文獻［3-4］基于Park變換和傅里葉變換，建立了混合動力汽車的永磁同步電機模型，研究了電機參數對機電耦合系統的影響。Ishikawa［5］忽略傳動系統內部作用，建立了包括永磁同步電機模型及簡化為慣性轉子的傳動系統模型，闡述了電動汽車機電耦合系統容易受到電機轉速和傳動系統負荷影響的特性。文獻［6-8］忽略了傳動系統齒輪嚙合產生的非線性力，建立高速列車牽引-傳動系統的機電耦合動力學模型，研究電機參數對機電耦合系統動力學特性的影響。以上研究主要集中在電機電磁作用下的電磁轉矩脈動方面，很少考慮齒輪傳動系統機械動力學特性。于蓬等［9-10］建立了包括電機的Park變換模型和傳動系統柔體模型的電動汽車電驅動系統機電耦合動力學模型，研究了控制策略對機-電-磁多物理場耦合下的電驅動模型的影響，并分析了穩定轉速下電機電磁剛度對系統振動特性的影響規律。張立軍等［11］對某燃料電池轎車在加速啟動和回饋制動的縱向振動問題進行了分析，考慮齒輪齒側間隙和輪胎-地面的摩擦動力學，建立了電機-減速器模型，發現在電機轉矩瞬間下降時，齒輪齒側間隙的存在會導致齒輪拍擊產生振動和噪聲。文獻［12-15］建立了包括截割電機和截割傳動系統的采煤機截割系統動力學模型，研究了變速變載工況下，內外激勵對機電耦合系統扭振的影響。

以上文獻大多聚焦在采煤機截割系統、高速列車牽引系統及永磁同步電機等領域的機電耦合動力學分析，而在電動汽車電驅動系統機電耦合方面研究相對較少。部分文獻雖建立了較為復雜的電動汽車電驅動系統機電耦合模型，但大多將依據經驗或實驗數據獲得的電磁激勵作為已知先驗函數施加于電機轉子，無法滿足非穩態運行工況。

本文中以某電動汽車電驅動系統為研究對象，首先建立了包括兩級減速器、永磁同步電機在內的齒輪傳動系統扭轉振動模型、基于d-q軸變換的永磁同步電機Park模型，在此基礎上建立電驅動系統機電耦合動力學模型。仿真分析穩態工況、沖擊載荷工況、起伏路面工況等3種工況下的電驅動系統機電耦合動態響應，揭示電驅動系統電機與齒輪傳動系統的機電耦合關系，為進一步研究電動汽車電驅動系統主動減振控制策略提供參考。

1 電動汽車電驅動系統機電耦合動力學模型

圖1為電動汽車電驅動系統結構示意圖，主要結構包括永磁同步電機、齒輪傳動系統等。

圖1 某電動汽車電驅動系統結構示意圖

1.1 永磁同步電機模型

齒輪傳動系統由永磁同步電機驅動。采用Park變換，在d-p坐標軸下建立永磁同步電機的等效電路模型。對應的電機電壓方程和電磁轉矩方程為

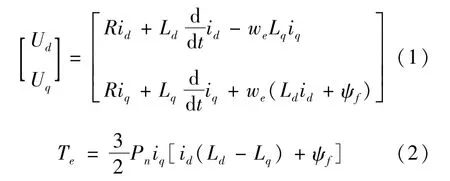
式中：Pn為電機極對數；Ud、Uq分別為d、q軸電壓；id、iq分別為d、q軸電流；Ld、Lq分別為d、q軸電感參數；ψf為永磁體磁鏈參數；we為基波電壓角速度；R為電機定子電阻；ψd、ψq分別為d、q軸上的永磁體磁鏈分量。

1.2 齒輪傳動系統扭轉振動動力學模型

1.2.1 齒輪副嚙合力模型

忽略傳動軸的橫向和軸向變形，僅考慮齒輪的扭轉振動，建立2自由度齒輪副扭轉振動模型，如圖2所示。

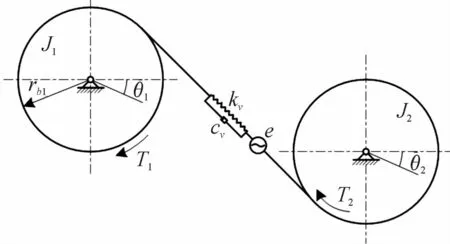
圖2 齒輪副嚙合模型示意圖

計入嚙合阻尼的齒輪動態法向嚙合力可表示為：

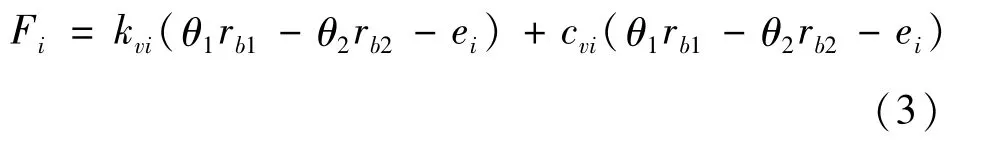
式中：i為參與嚙合的齒輪序號，i=1，2；kvi、cki為齒輪對i在嚙合點處的綜合嚙合剛度和阻尼系數。

主、從動齒輪的力矩平衡方程為：

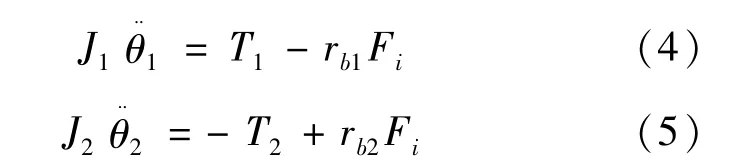
式中：θ1和θ2分別為主、從動齒輪的轉角；J1、J2分別為兩輪的轉動慣量；T1、T2為驅動力矩和阻力矩；e1、e2為齒廓誤差。用x表示齒輪動態傳遞誤差，x=θ1rb1-θ2rb2-e（t），則間隙函數為：

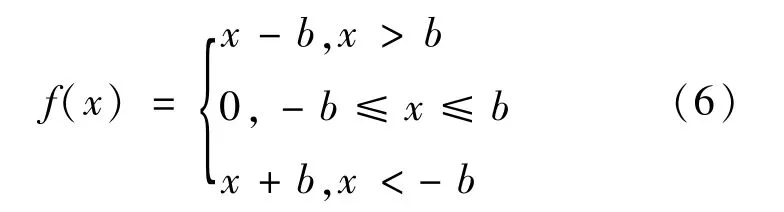
式中：2b為齒輪副間隙；當f（x）=x-b時，輪齒處于正常嚙合狀態；當f（x）=0時，輪齒處于分離狀態；當f（x）=x+b時，嚙合輪齒處于齒背嚙合狀態。

1.2.2 齒輪系統扭轉振動動力學模型

圖3、4所示分別為齒輪傳動系統模型和齒輪傳動系統扭轉振動動力學模型。綜合考慮齒輪傳動系統的剛體轉動和彈性扭振，建立傳動系統各構件的動力學方程，如式（7）所示。

圖4中，JM、JL、J1、J2分別為電機、負載和主、從動輪的轉動慣量；θ、θL、θ1、θ2分別為電機、負載和主從動齒輪的轉角；k1、k2分別為主從動軸的扭轉剛度系數；c1、c2分別為主從動軸的扭轉阻尼系數。

圖3 齒輪傳動系統模型示意圖

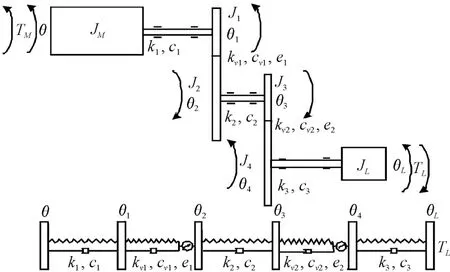
圖4 齒輪傳動系統扭轉振動動力學模型示意圖

考慮電機的特性，即計入電機的速度波動，取θ、θL、θ1、θ2為系統的廣義坐標，用牛頓-歐拉方法建立系統的動力學方程為：

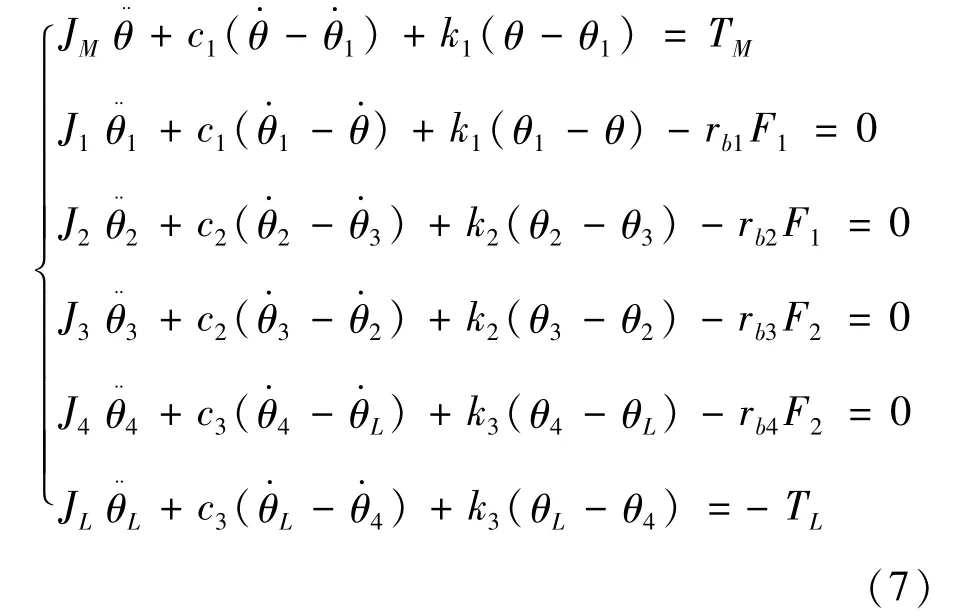
式中：rb1、rb2、rb3、rb4分別為4個齒輪的基圓半徑；F1、F2分別為第1對和第2對輪齒間的動態嚙合力：

式中：TM、TL分別為驅動力矩和負載力矩；cv1、cv2分別為齒輪嚙合阻尼系數；kv1、kv2分別為齒輪嚙合剛度系數。將TM、TL的變化規律代入式（7），求出電機的角度變化規律，即速度波動。

1.3 電動汽車電驅動系統機電耦合模型

電機通過磁場將電源的電能轉換為轉子的機械能，轉子直接和傳動系統相連，因此通過建立電機輸出轉矩等于傳動系統輸入轉矩的等式可將電氣系統和機械系統聯合到一起，從而得到電動汽車電驅動系統機電耦合模型，見圖5。

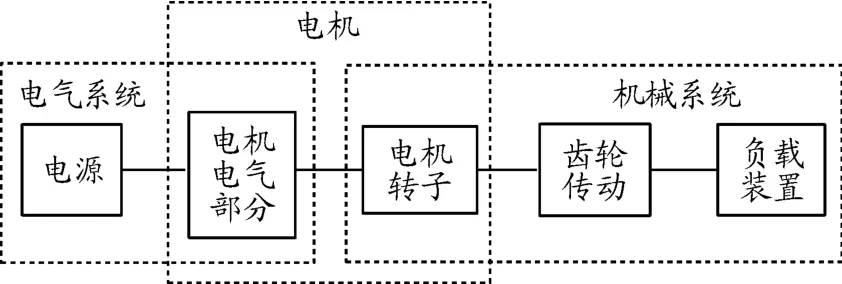
圖5 電動汽車電驅動系統機電耦合模型框圖

2 電動汽車電驅動系統機電耦合動態特性分析

以某電動汽車的電機和減速器為例進行研究，搭建某電動汽車電驅動系統機電耦合仿真模型。電驅動系統主要仿真參數如表1所示。

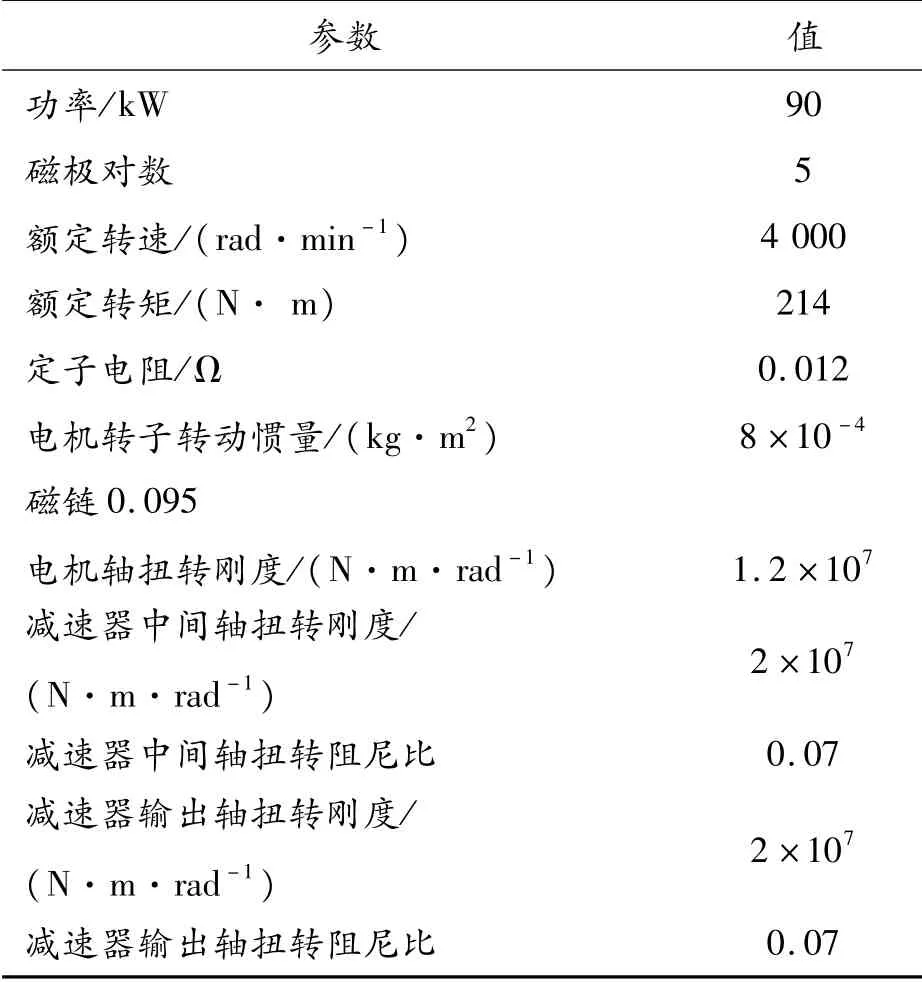
表1 電驅動系統主要仿真參數

2.1 穩態工況下對電驅動系統機電耦合動態特性的影響

為研究穩態工況下對系統的影響，對機電耦合系統施加恒轉速、恒負載工況分析齒輪傳動系統的動態響應和電氣系統的電信號動態響應。

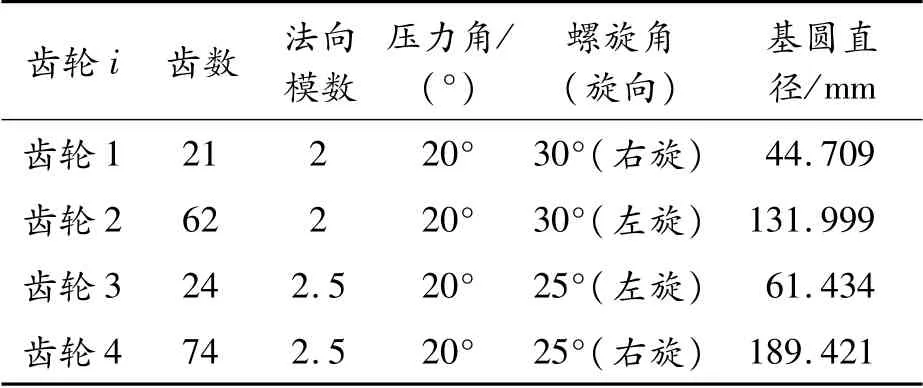
表2 齒輪傳動系統基本參數

圖6所示為電機轉速為4 000 rad/min時的傳動系統動態嚙合力響應圖。fmg（g=1，2）表示從電機到負載端的各級齒輪副嚙頻，fst（t=1，2，3）表示傳動軸轉頻（fm1=1 400 Hz，fm2=541.92 Hz，fs1=66.67 Hz，fs2=22.58 Hz，fs3=7.32 Hz）。傳動系統的嚙合力頻譜圖中含有2對齒輪副的嚙頻信息，但主導頻率還是第1對齒輪副的嚙合頻率及其倍頻。

電機轉速頻率中含有機械傳動系統的嚙合頻率及其倍頻（見圖7），表明電機轉速會受到齒輪嚙合力頻率的影響，降低電機轉速中嚙合力頻率的含量將會減小電機轉速波動。

圖6 電機負載214 N·m齒輪嚙合力動態響應

圖7 電機負載214 N·m電機轉速動態響應

圖8 為電流頻譜圖，其中含有豐富的傳動系統頻率信息，包括各級轉頻、嚙頻及其倍頻，但幅值較小。機械系統的頻率對電氣系統中的定子電流進行調制，表明電氣系統會受機械系統影響。

2.2 沖擊載荷對電驅動系統機電耦合動態特性的影響

為研究電驅動系統在沖擊載荷下的動態響應特性，對系統施加沖擊載荷進行仿真，并對機電耦合系統的動態響應進行分析。

對電機軸施加1個沖擊載荷（如圖9），在0.2 s時從0.5Tn階躍至1Tn（Tn為電機額定負載轉矩）。

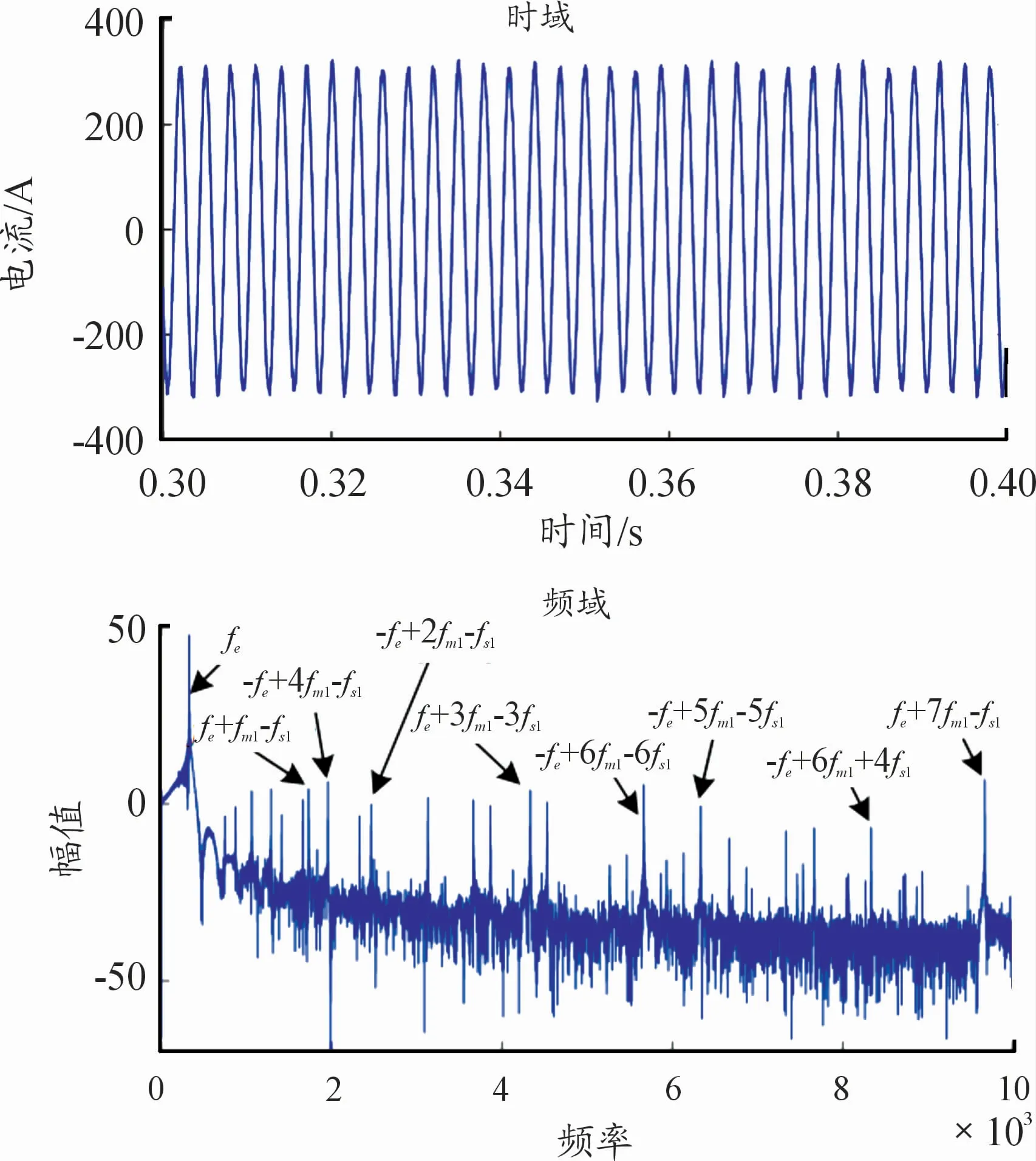
圖8 電機負載214 N·m電機定子電流動態響應

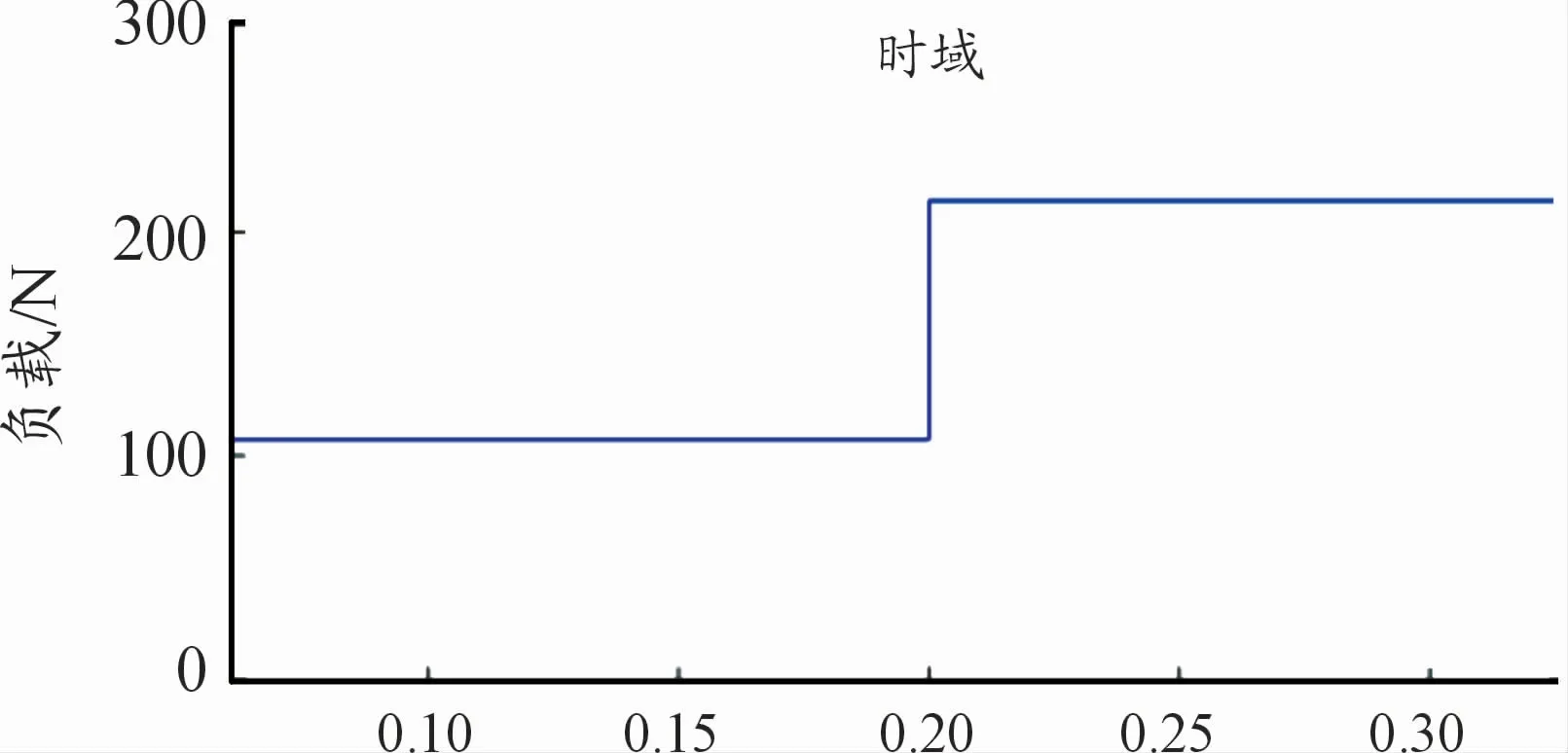
圖9 電機軸沖擊載荷

圖10 、11分別為電機軸動態轉速響應和齒輪動態嚙合力響應。

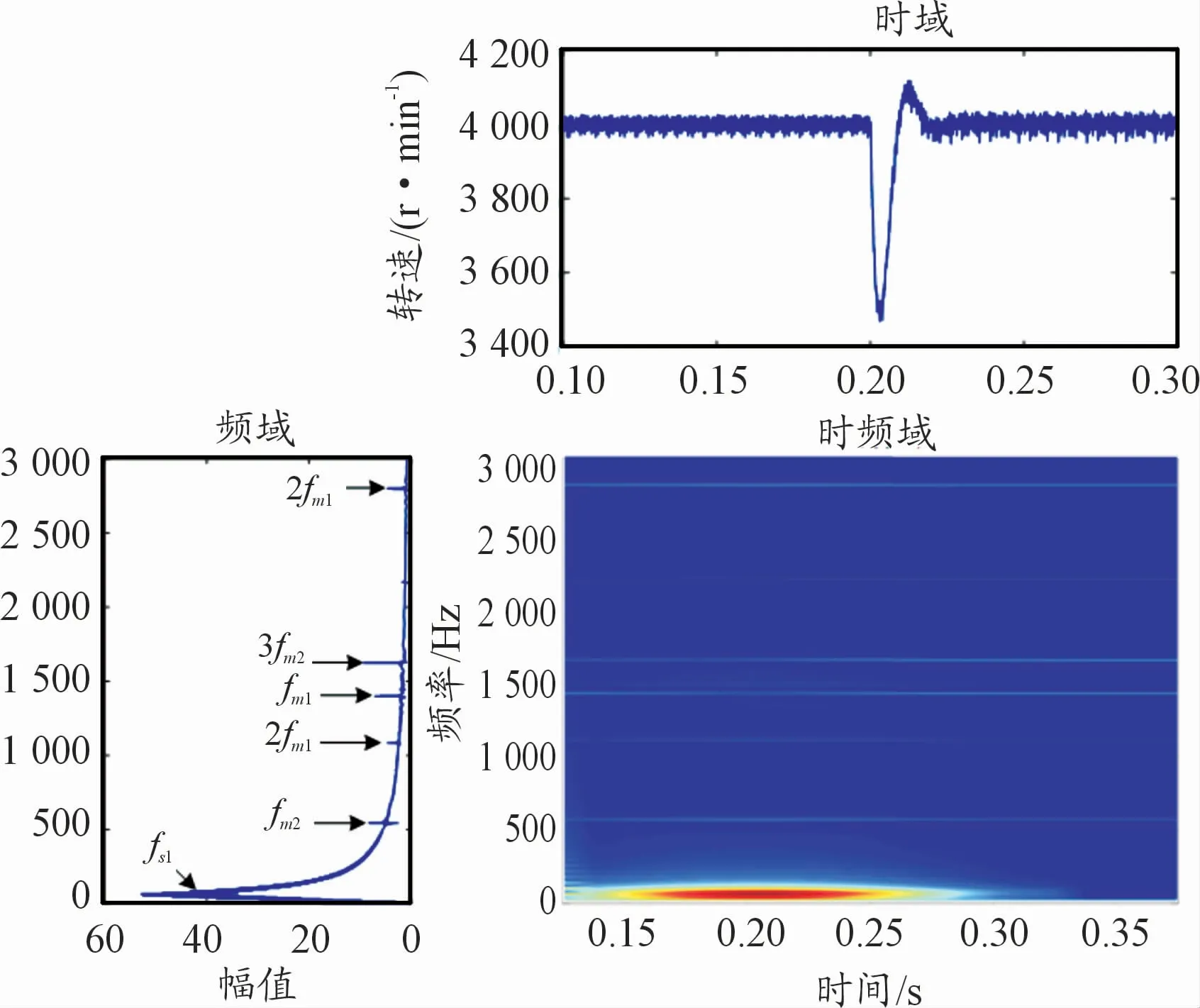
圖10 沖擊載荷下電機轉速動態響應

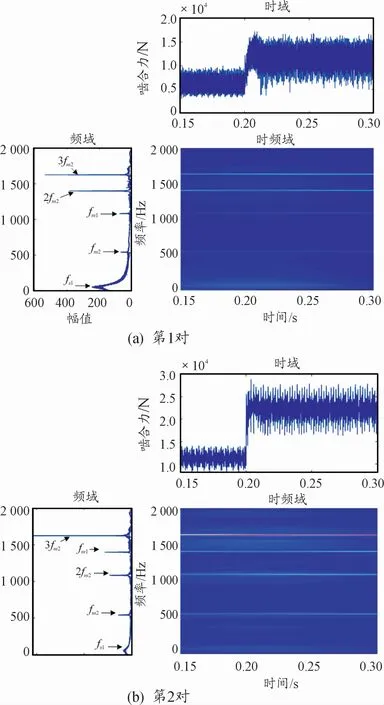
圖11 沖擊載荷下齒輪嚙合力動態響應

在0.2 s時負載突變，電驅動機電耦合系統受到沖擊后，傳動系統嚙合力、電機軸轉速、定子電流的相應頻率及其倍頻的幅值都會瞬間增大。特別是電機軸轉頻幅值和齒輪嚙頻幅值變化明顯，更容易因扭振而產生傳動軸的斷裂，導致齒輪的損壞對電動汽車的安全性造成威脅。設計傳動系統時應考慮該問題。

圖12為負載突變過程中電機定子動態電流響應。在頻域圖中，定子電流頻率包含電流頻率和微弱的齒輪嚙頻及軸轉頻，且電流頻率受到傳動系統頻率的調制。當負載發生突變時，電流頻率會發生突變，表明電氣系統會受到傳動系統瞬態振動的影響。

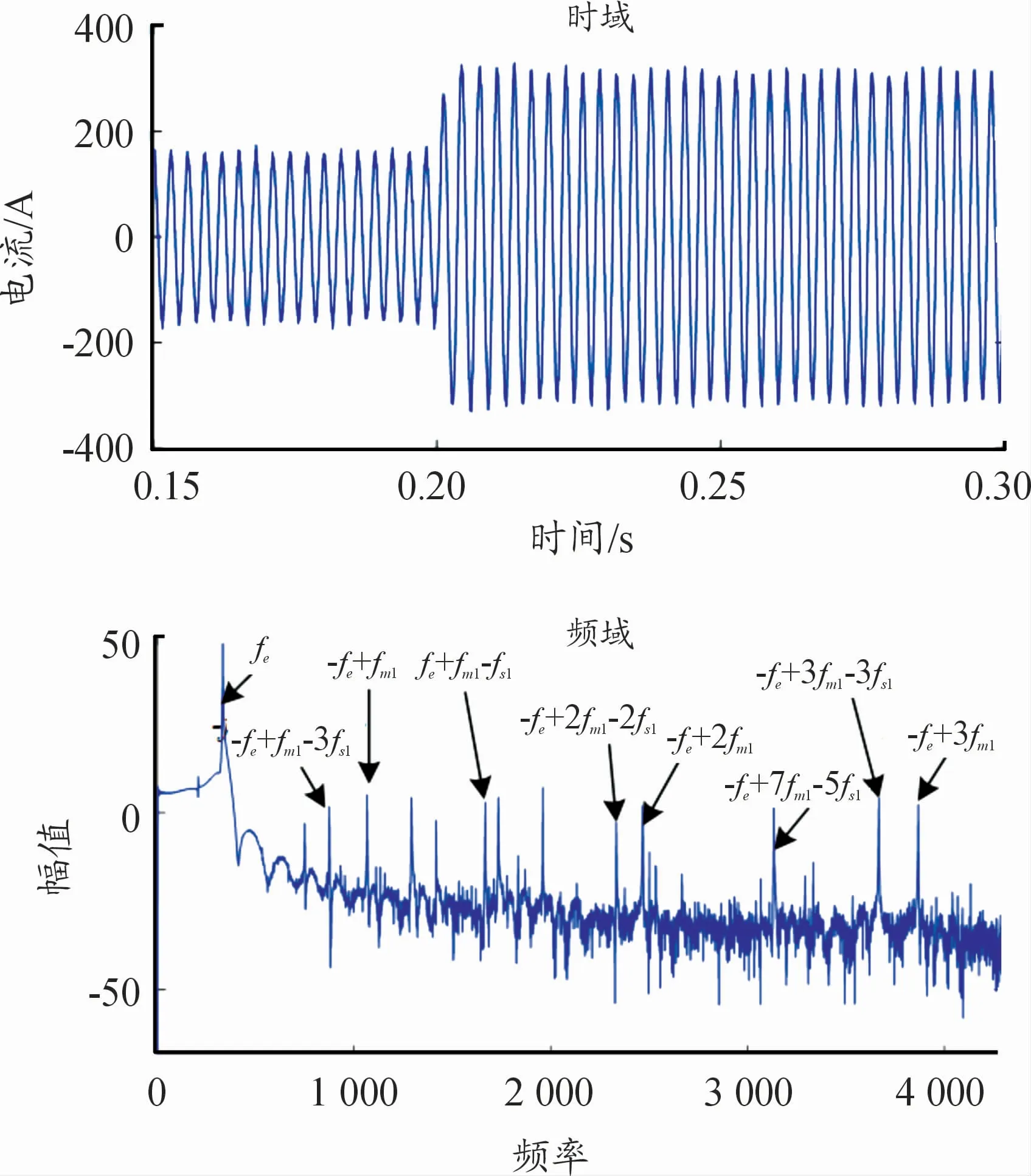
圖12 沖擊載荷下電機定子電流動態響應曲線圖

2.3 正弦波動載荷對電驅動系統機電耦合動態特性的影響

電動汽車行駛時常會面臨各種路況。穩態工況和沖擊載荷工況僅是車輛行駛工況下的一部分，還有在起伏路面行駛的工況。因此僅對穩態和突變載荷工況進行仿真分析不足以表明典型工況下電動汽車的機電耦合系統響應特性。于是采用正弦函數（頻率為7 Hz）來模擬起伏路面工況下的負載（如圖13），研究起伏路面下電動汽車電驅動系統的機電耦合動態特性。

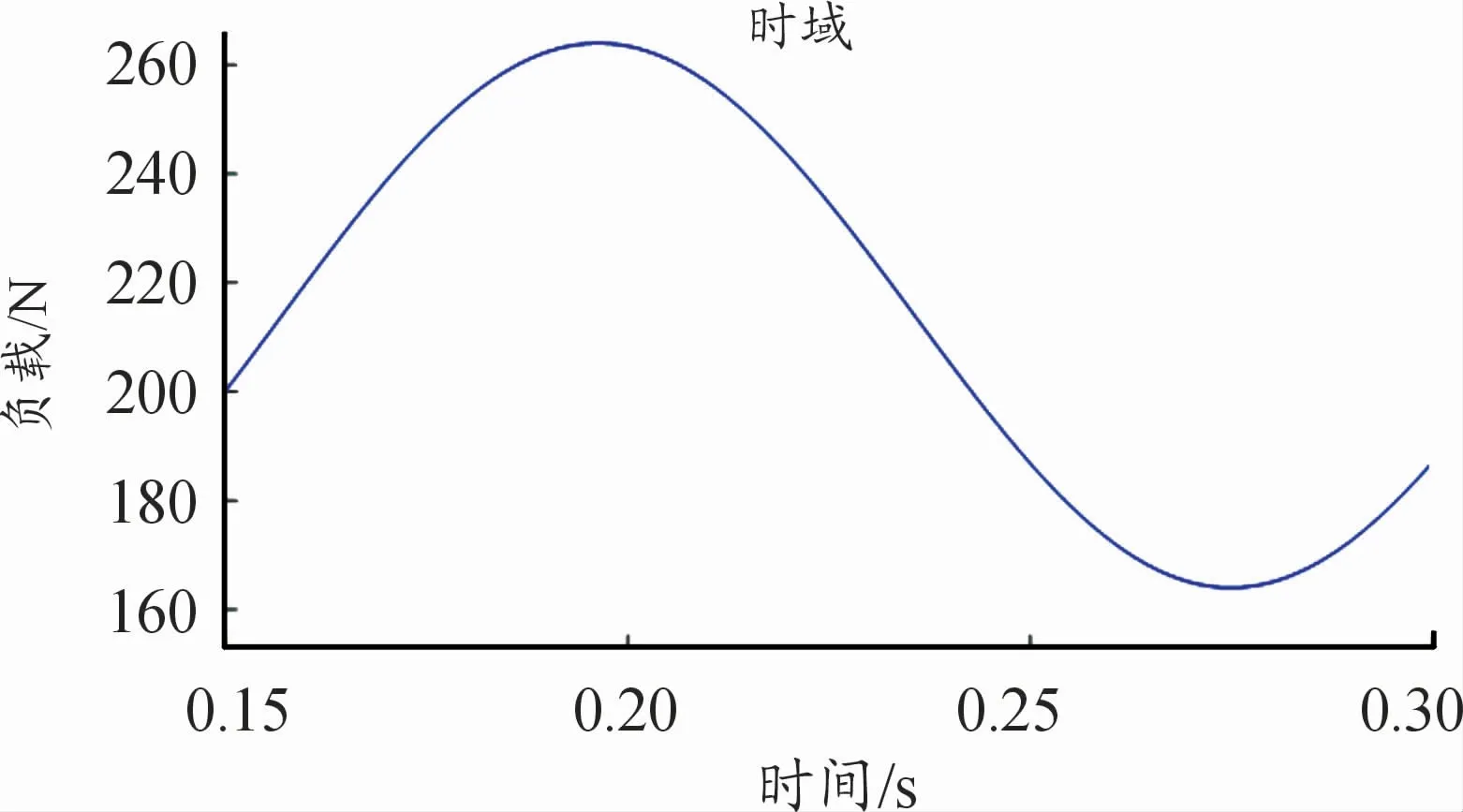
圖13 系統負載轉矩曲線圖

如圖14～16所示，隨著負載呈正弦波變化，電機輸出轉速、齒輪嚙合力、電機定子電流整體上也呈現正弦變化；和沖擊工況下幅值明顯增長相比，該工況對嚙合力頻率幅值影響不大，表明在負載變化緩慢的工況下，有利于減小電動汽車電驅動系統的扭轉振動，延長零部件使用壽命。

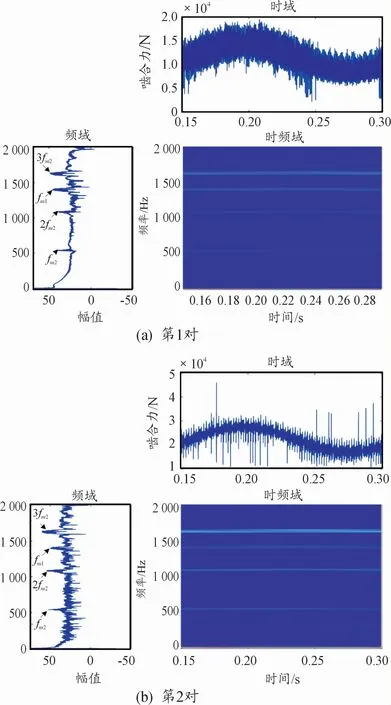
圖15 正弦波動載荷下齒輪嚙合力動態響應曲線圖

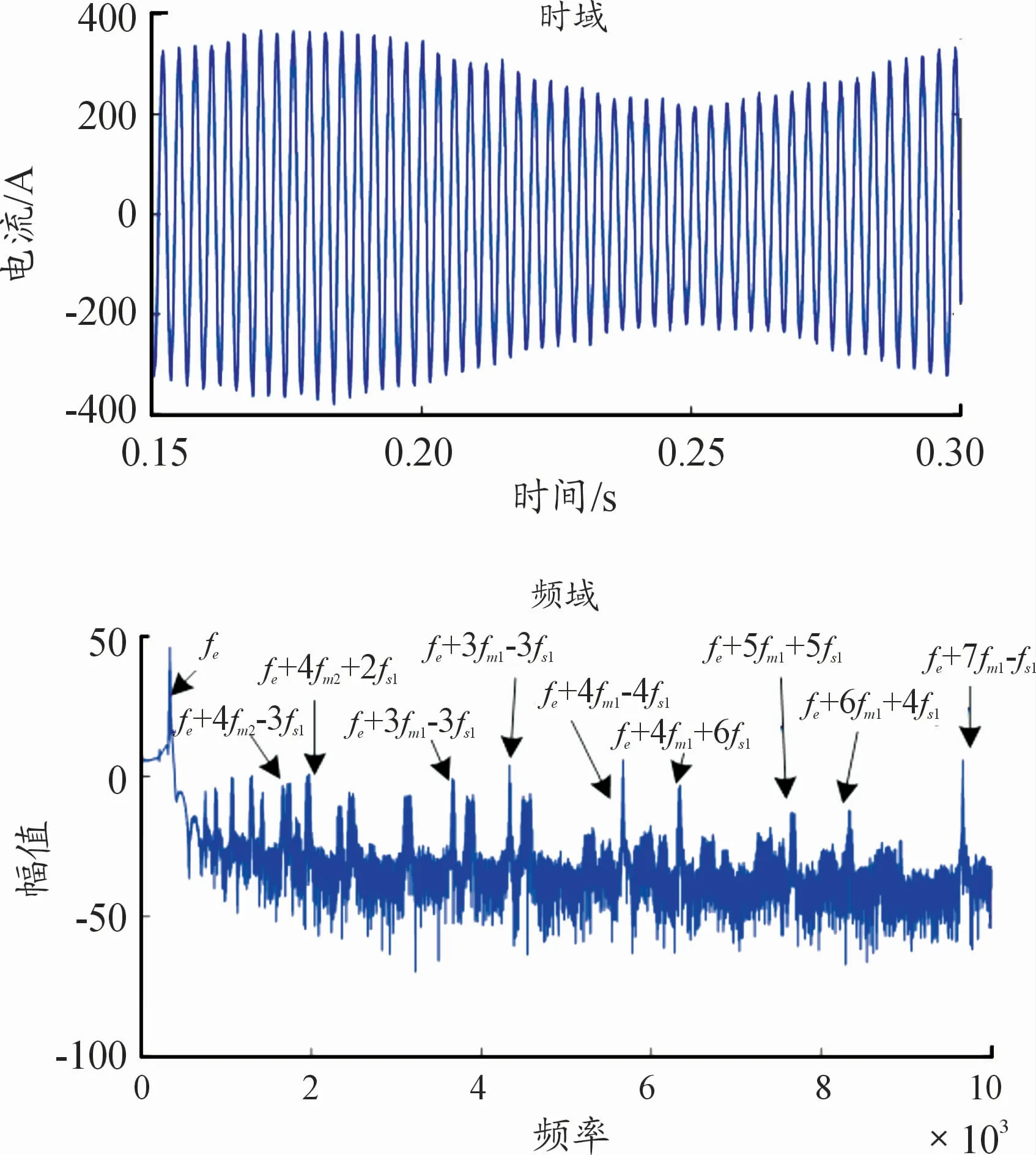
圖16 正弦波動載荷下電機定子電流動態響應曲線圖

電流信號中含有的機電耦合信息比轉速及嚙合力更加豐富，因此可用電流來監測典型工況下機電耦合系統運行狀態，與分析相符。綜合3種工況下的電流頻譜圖來看，負載突變工況下的電流頻譜圖包含的傳動系統頻率信息最明顯，即該工況下定子電流信號監測傳動系振動狀態的效果最好。

3 結論

1）電機轉速頻譜中含有齒輪傳動系統的各級齒輪嚙頻。定子電流被傳動系統的嚙頻和轉頻調制，使得電機定子電流中含有豐富的傳動系統頻率信息。表明電驅動系統的電氣系統受機械傳動系統扭振影響；電機與傳動系統之間存在明顯的機電耦合效應。

2）與電機轉速相比，由于電機定子電流信號含有更加豐富的齒輪傳動系統頻率信息，因此可通過分析電機定子電流頻率信號來監測齒輪傳動系統嚙合振動狀態，特別是在負載突變工況下，電流頻譜圖包含傳動系統頻率信息最明顯，即該工況下定子電流信號監測傳動系振動狀態的效果最好。