梁格法在城市橋梁設計中的應用研究
董 營,劉 松
1.山東省路橋集團有限公司,山東 濟南 250014
2.濟南市市政工程設計研究院(集團)有限責任公司,山東 濟南 250003
近些年,柔性橋、箱梁橋等結構形式陸續出現,為確保其施工與使用過程的安全性,為城市經濟發展做出更大貢獻,相關部門應分析其結構的空間內力分布與變形情況。其中,梁單元法、板殼元法及梁格法等均是常用方法。相比之下,梁格法的計算成本相對較低、能較快捷地提取計算結果且還能和現行橋梁建設規范相匹配,目前梁格法在橋梁工程分析領域有較廣泛的應用。文章基于梁格法的基本原理,參照現實案例,歸納梁格法在城市橋梁設計中的應用情況。
1 梁格法的基本原理
梁格法是利用一個等效的梁格將橋梁上部結構取而代之,可以將其看成是一種將梁作為基本單元的有限元法。該方法在應用階段表現出概念明確化、便于理解與操作使用、測算較快速等特點。目前國內現有的計算曲線梁橋的軟件,如《橋梁博士》等,均應用了梁格法。
梁格法用于工程領域的主要思路是用一個等效的平面梁格或者空間構架去仿真模擬上部結構,把分散于板式或箱梁各個區段中的彎曲及抗扭剛度聚集在相毗鄰的等效梁格中,真實結構的縱向、橫向剛度則分別被集中在縱向、橫向梁格構件中。通過分析該平面梁格或空間構架,能夠較順利地獲得實體橋梁上部結構縱、橫向內力分布與變形狀況。對于箱形截面而言,如果把腹板設定為基本單位劃分梁格,則據此便能夠獲得腹板的真實受力特征,可以直接利用其計算出腹板的配筋,借此方式規避既往用空間梁元與空間箱形梁元分析階段務必橫向配置各個腹板內力的流程,使工程設計工作更簡單、快速地推進。梁格法在應用階段的關鍵點在于其和橋梁上部結構形成了等效性,等同于在相等荷載作用下維持兩者內力分布與變形狀態一致,這就預示著是否能達到等效性直接影響結構分析結果的準確度。
2 梁格法單元劃分及截面計算
2.1 梁格單元劃分
整體而言,一定要參照橋梁上部結構與支座狀況,并結合結構力學有關原理及既往形成的工程施工經驗進行梁格劃分,梁格劃分應遵循的常規規則如下。
(1)盡可能使梁格和設計受力線相互重合。例如,和預應力或梁構件成角180°,順沿邊梁及支座上的受力線等進行操作,借此方式實現對橋梁結構作業狀態的有效模擬。
(2)盡量使梁格符合原型結構內力分布狀態。比如,在板橋梁格對應的等效模型內,明確要求各根邊緣梁格一定要臨近上部結構邊界位置并和剪力流的合力相互垂直。
(3)盡可能使梁格橫、縱向構件間距值接近,借此方式增加梁格結構對荷載的靜力分布狀態的靈敏度。
(4)劃分平面梁格模型時,盡量使各部分的形心軸與整體的形心軸方位等同。
2.2 梁格截面計算
加載具體方位與不同單元之間的相對剛度是梁格法配置荷載的主要依據,構件截面特性是影響剛度值高低的主要因素之一,故而準確測算出梁格單元的截面特性能使最后測算結果的精確度得到更大保障。
就板式上部結構而言,可以依照正交各向同性板測算出鋼筋砼及預應力砼實體板橋,參照以下公式測算出截面特性:

式中:i、c分別為單位板寬構件的慣性矩和有效抗扭常數;h為板的厚度。
對于箱梁而言,通常會把縱向構件細化成數個工字梁,縱向單元特性測算過程較為簡單,其實便是采用相對應的工字梁面積、抗彎慣性矩以及腹板橫截面面積分別表示縱向單元面積、抗彎慣性矩、抗剪面積。可以將橫向單元看成是由上下兩塊板共同構成的空腹斷面,于荷載作用下統一環繞它們的共同重心水平中性軸彎曲。橫向梁格面積等于其所代表范疇中頂底板的面積總和,可以利用以下公式計算出慣性矩按繞板的共同重心:

式中:d'、d〃、h'、h〃為板的厚度及各板至其形心的距離值。
當箱梁結構進行整體扭轉時,大部分的剪力流環繞頂板、底板與腹板的周界進行流動,僅有極少部分會流經中間腹板。解讀剪力柔性梁格相關理論,在頂板與底板內的相逆剪力流共同作用下形成了上部結構中的扭矩,頂板與底板是提供抗扭剛度的主體構造,可以采用以下公式測算出單位縱向或橫向梁格構件的抗扭常數:
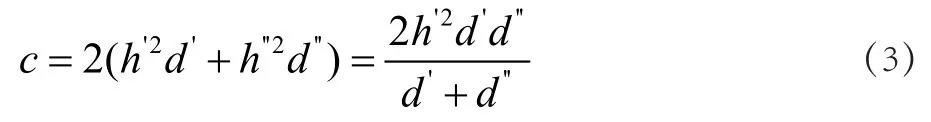
3 工程應用案例
現有一座雙跨連續鋼筋砼實心板橋,橋面寬為12.9m、長為40m,主體橋面寬度×高度為8m×1m,兩側翼緣寬,高度分別為2.4m、0.4m。橋梁工程建設階段所用的砼材料基本參數如下:密度為2600㎏/m3,彈性模量為35GPa,泊松比為0.168。利用梁格法測算其結構受力特征,并且和實物體有限元計算結果進行比較分析。參照梁格法形成的理論,先劃分梁格與測算出單元剛度等效數值,劃分梁格期間為了確保最后測算結果的精確性,該工程依照橫向1m寬度進行分析,兩側2.4m的翼緣均依照1.2m梁格規格確定,縱向尺寸為1m。梁格的具體劃分情況如圖1所示,參照劃分出的梁格單元測算出其對應的等效剛度。在以上過程中應關注因左右兩側翼緣的高度存在差異而造成其截面形心方位和主體界面存在一定不同這一現實情況,并且具體測算階段應考慮對梁格2~3以及10~11安設橫向剛性銜接,借此方式使兩者受力狀態與變形程度的統一性得到更大保障。

圖1 梁格劃分圖示
應用梁格法與實體有限元方法測算出自體重量作用下沿著橋向梁體的彎矩結果,如表1所示。通過比較分析不難發現,梁格法下的計算結果和實體有限元計算結果兩者的吻合度相對較高,誤差基本被控制在6.0%以下,不管是對整體的彎矩狀況或者是對特殊構件3的彎矩配置,均較好地證實了梁格法計算結果的準確性,在城市橋梁設計計算領域有較高的適用性。
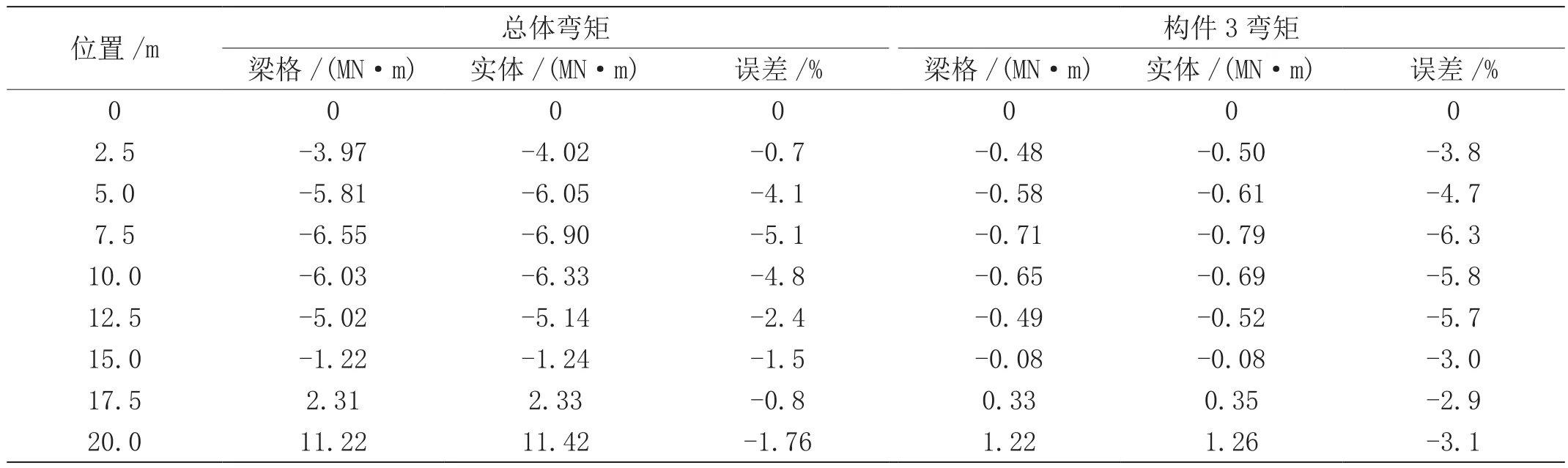
表1 梁格法的計算結果和實體有限元計算結果比較
4 結束語
梁格法是當下橋梁工程建設階段分析橋梁結構空間的一種常用方法,其在應用階段能取得較理想的結果。梁格法有概念清楚明確、便于理解與操作使用等諸多特征,在城市橋梁的寬梁橋、斜交橋等多種結構型式中表現出了較高的適用性。文章在分析梁格法基礎理論的基礎上,解讀了梁格劃分與剛度計算兩個主要問題,利用實際工程案例對梁格法的計算結果和實體有限元計算結果進行了比較分析,兩者形成的誤差被控制在6.0%以下,說明梁格法的精確度較高,在橋梁工程結構分析中有較高的推廣價值。

