基于遺傳算法對環形輸送線調度優化研究

章俊哲，李金村，徐 健，吳宗毅，王 鵬

（1.北京機械工業自動化研究所，北京 100120；2.北京機械工業自動化研究所有限公司，北京 100120；3.北自所（北京）科技發展有限公司，北京 100120）

0 引言

在當今全球化和市場化的潮流下，物流對于促進世界經濟、貿易和電子商務的發展有著巨大的意義。輸送線是物流倉儲中心的重要組成部分。托盤和貨物都需要經過輸送線送至目的地，輸送線的效率和穩定性決定了整個系統的效率。輸送線就像是人體中的血管，對整個系統起到了至關重要的作用。

隨著物流規模的擴大，很多學者開始對其中的環節進行研究和優化。賀道坤等人為了解決環形輸送線揀選問題，利用條碼識別的方法對不同工件進行分揀[1]。王鵬等人為了解決紙箱自動輸送的效率能夠滿足生產需求，對PLC控制程序進行了優化[2]。劉煥牢等人為了解決生產線效率和人工等問題，對輸送線的機械結構進行了分析，使得系統實現了全自動化且節約了人力[3]。以往的學者對輸送線的研究基本上都在于對機械結構和控制程序的方面，很少有對于輸送線調度程序方面進行優化。

本文根據約束松弛條件對輸送線系統建立數學模型，再通過遺傳算法對系統進行研究。利用仿真，找到系統的最優解，根據比較得到遺傳算法對系統的優化效果。

1 遺傳算法介紹

1.1 遺傳算法概述

遺傳算法是基于達爾文進化論和孟德爾的遺傳學說所推理出來的。遺傳算法模擬自然界中生物繁衍和進化的過程，將有利種群的特征得到延續，由此發展出的全局概念法[4]。遺傳算法借鑒生物進化中的一些思想，通過生成種群、自然選擇、交叉、變異等操作，增強想要得到的屬性。

遺傳算法其中包括幾個重要的條件：

1）個體指帶有特征的實物，生物學中也成為染色體。個體通常的表現方式為二進制串和符號串等。

2）基因是染色體中的某些特征單位，代表了個體的獨有特性。

3）種群是由所有個體組成的群體。在遺傳算法中，群體的規模一般設置為10～100之間。

4）適應度是指個體對于約束條件的適應情況。能夠更好適應約束條件的個體，有更高的概率進行遺傳，將基因傳遞給下一代。

5）編碼是指將現實問題的解映射到遺傳空間。

6）解碼是指將遺傳空間的解映射到現實問題。

7）遺傳算子是遺傳算法模擬生物進化的重要手段。其中分為三種：選擇算子、交叉算子和變異算子[5]。

1.2 遺傳算法的基本流程

1）設置遺傳所需要的具體參數。

2）將現實問題映射至遺傳空間，進行編碼。

3）生成初始化種群。

4）找到適應度函數進行計算，根據計算出的個體適應度，選出合適的個體進入下一代。

5）交叉變異。

6）不斷地迭代，直到滿足算法的終止條件。將種群中適應度最高的解輸出，作為最優解。

2 實例分析

2.1 系統概述

圖1是A廠的環形輸送線示意圖，主要設備為輥筒輸送機。

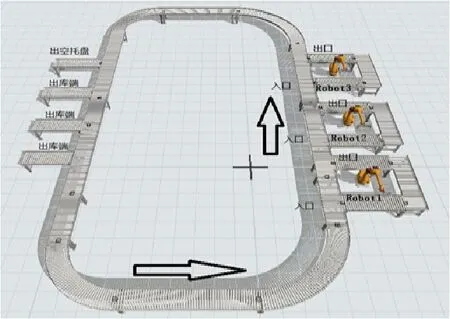
圖1 A廠環形輸送線系統示意圖

圖1左側為入環形輸送線端口，右側為拆垛區域。托盤由輸送線輸送至拆垛區域。每個拆垛區域由機器人和輸送線組成，分別有一個入滿托盤口和出空托盤口。托盤在拆垛完成以后，空托盤經過環形輸送線運送至出口。空托盤匯入輸送線不會影響滿托盤的輸送節拍。

2.2 環形輸送線調度模型建立

本章將針對環形線體系統的托盤調度問題進行研究，對于傳統的輸送線而言，托盤是否進入線體和送出線體僅僅依靠人為設置好的去向去分配，托盤會按照均分進入或者送出輸送線的原則進行分配。這種方法不會根據實際情況進行調節，從而導致整體效率下降。

本文將用遺傳算法對環形輸送線貨物的調度系統進行優化。該系統的布置示意圖如圖2所示。

圖2 環形輸送線系統示意圖

圖2中，Ei表示入環形輸送線的端口，Uj表示出環形輸送線的端口。為了簡化系統便于研究問題，該系統的約束松弛條件如下：

1）線體為單向運行（逆時針），不能反轉。

2）每段輸送線只能存放一個托盤。

3）輸送線被分配任務以后，到達相應的出入端口，立即執行，不存在等待時間。

4）每送出14個托盤被視為一個調度任務周期。

5）輸送線在運行過程中，若發生故障，則停止系統的調度，不會對整體系統的調度優化過程造成影響。

6）L1、L2和L3入環形輸送線端口的貨物視為無窮，進入輸送線順序按照分配進入。

托盤一次作業包括進入線體、輸送、托盤送出線體三個過程，三個過程所用時間為：

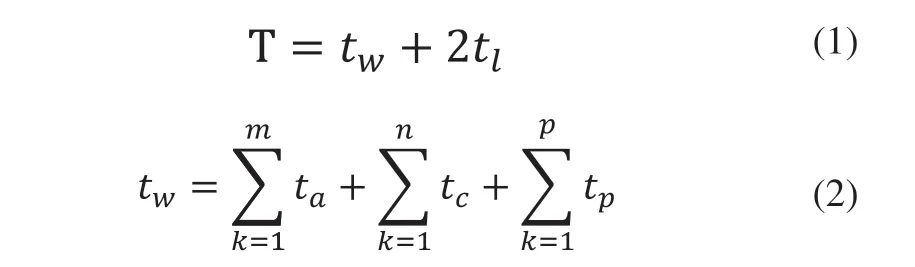
上式中，T為輸送機完成一次輸送作業所需的時間，tw為托盤運行在輸送線上花費的時間，它包括托盤加減速ta，托盤勻速行走時間tc和托盤等待向前輸送時間tp。tl為托盤出入線體的輸送時間（定值）。由以上公式可以推出，tw決定了整個系統的運行時間。而tw和托盤在輸送過程中是否出現堵塞相關。線體堵塞越嚴重，輸送時間就越長。想要優化整個系統的效率，可以從減少堵塞次數這方面解決問題。

根據提出的解決方案，建立相應的數學模型：

式(3)中，Bc（q）為第n個托盤內由于前方輸送機堵塞而等待的次數，即

約束條件：

2.3 改進單親遺傳算法設計

2.3.1 染色體編碼

將托盤的隊列進行編碼，具體編碼方式如下：

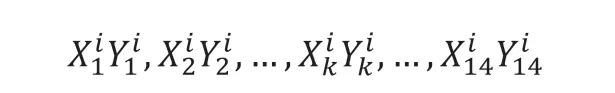
編碼方式中的Xik表示第k個托盤在第i周期進入線體的起始端口，Yik表示第k個托盤在第i周期被送出線體的目的端口。例如0103表示托盤先在E1口進入線體，再去U3被送出線體，進入拆垛區域，即托盤完成本次作業。

2.3.2 初始化種群

種群規模過大或過小對實驗效果均不好，故設置種群規模為50。單個染色體形成的具體方法為：

托盤進環形線體端口為：P1，…，Pk，…，Pk+i，…；

托盤出環形線體端口為：Q1，…，Qk，…，Qk+i，…；

從托盤進環形線體端口中隨機選取Pk賦給從托盤出環形線體端口中隨機選取Qk賦給再從托盤進環形線體端口中隨機選取Pk+i賦給從托盤出環形線體端口中隨機選取Qk+i賦給直到形成合格的染色體為止。

2.3.3 適應度函數

適應度函數是判斷種群中個體好壞的標準，根據以上分析可得到相應的目標函數：

堵塞次數最少：

為了解決目標問題，將適應度函數定義為在一個周期內找到問題。本章將把問題用一個適應度函數表示：

其實把問題簡化為了找到F的最小值，即在一個調度周期內的擁堵次數的最小值。我們將具體說明適應度值的計算過程。

隨機生成一組染色體：

0205，0107，0304，0202，0304，0106，0303，0306，0101，0107，0205，0305，0306，0102

堵塞次數如下計算：

例如0205，0107這樣的基因串就會有堵塞的情況，前托盤先在2號入口進線體，去5號出口送出托盤。后托盤在1號入口進入線體，去7號出口送出托盤，若前托盤走過1號端口則在送出托盤的過程中，會導致后托盤堵塞一次。若前托盤沒走過1號端口則在1號端口送托盤的過程中，會導致前托盤堵塞一次。故不管出現什么情況，均會導致堵塞一次。0107，0304這樣的基因串不會出現堵塞，前托盤先在1號入口進線體，去7號出口送出托盤。后托盤在3號入口進入線體，去4號出口送出托盤，故不會堵塞。可以得到當時，會使托盤擁堵一次。

2.3.4 遺傳算子設計

本文選擇算子采用混合選擇的方法，即采用保留優秀個體和輪盤賭法結合。具體操作如下：

第一步隨機生成染色體，將適應度大于平均適應度的個體去除，保留下適應度小于平均適應度的個體。保留下來的個體進入下一代；

第二步利用輪盤賭法將去除的個體進行選擇，與第一步中保留下來的個體組成下一代種群。

得到的種群在利用基因重組的方法進行單點換位算子，對每代染色體個體中進行m次單點換位，計算模型如下：

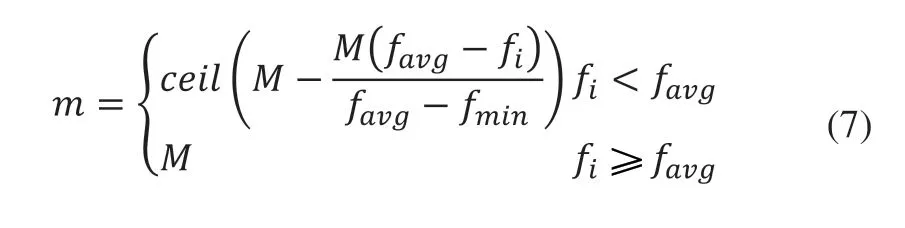
式(7)中ceil是向上取整，fmin是種群中個體的最小適應度，favg是種群的平均適應度，fi是要單點換位的個體的適應度，M為定值，即最大次數，設為5。

2.3.5 終止條件

在遺傳算法中，通常由兩種終止條件：第一種是得到最優解以后算法終止。第二種是迭代至設置的值以后算法終止。本文采用第二種方法，設置迭代次數為500次。

3 仿真分析

3.1 仿真建立

通過上面分析，通過MATLAB進行編程，可以得到詳細的算法，本文將以改進的單親遺傳算法對貨物調度系統模型進行優化，具體步驟入圖3所示。

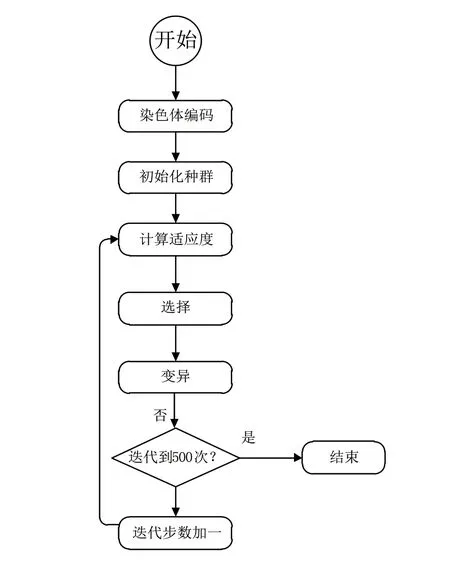
圖3 遺傳算法MATLAB設計流程圖

3.2 仿真數據分析

利用MATLAB進行仿真。利用上文中的方法進行數據仿真，進行分析。

1）隨機生成一個調度周期內的作業，如下：

托盤進環形線體作業：01，03，02，01，02，03，02，01，03，02，01，02，03，02；

托盤出環形線體作業：05，06，02，03，01，07，04，06，02，05，01，07，01，03；

2）隨機生成初始化種群，如下：

0105，0306，0202，0103，0201，0307，0204，0106，0302.，0205，0101，0207，0301，0203。

按照算法計算可得到堵塞次數為7 次。利用MATLAB軟件進行仿真，得到最優解個體如圖4所示。

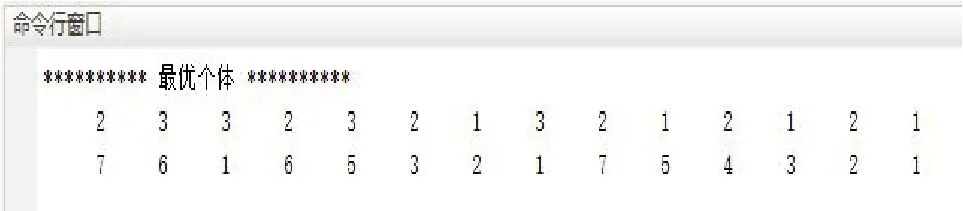
圖4 第一次調度周期最優個體

最優解個體的堵塞次數為2次。

其中一個最劣解個體堵塞次數為9次，具體如圖5所示。

圖5 第一次調度周期最劣個體

圖6和圖7分別為最優解隨進化代數的變化趨勢和平均值隨進化代數的變化趨勢。從圖6可以看出最優解的堵塞次數在20代左右出現變化，進化到180代左右收斂得到了種群中的最優解個體。圖7的變化趨勢與圖6基本一致，也是在180代左右收斂最佳。

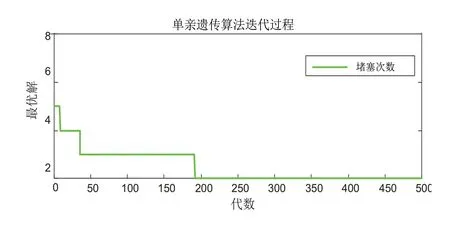
圖6 最優解隨進化代數的變化趨勢

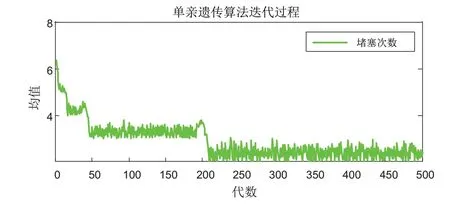
圖7 平均堵塞次數隨進化代數的變化趨勢

利用上述方法將得到第二次周期，第三次周期的變化趨勢，進行比較，如表1所示。

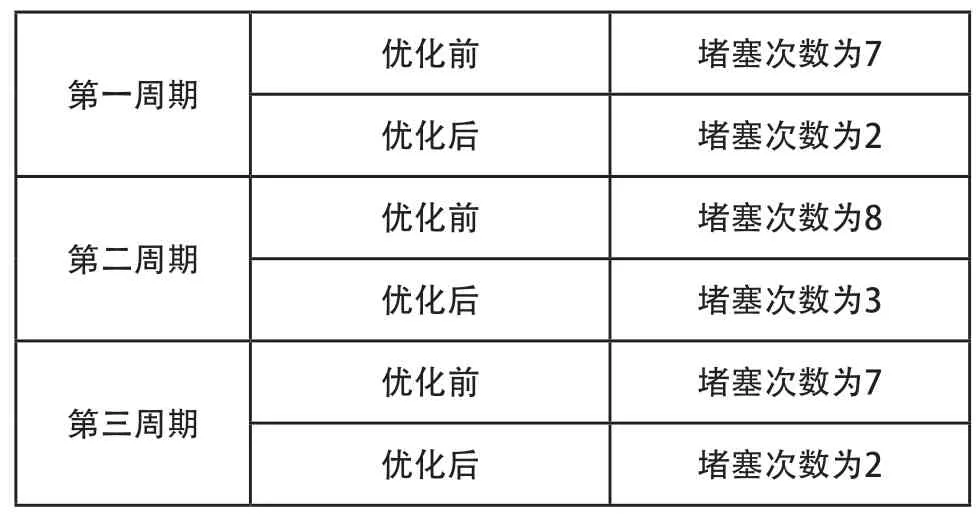
表1 優化前后堵塞次數

由表1可以根據仿真優化前后得出環形線經過本文設計的遺傳算法模型，減少一個周期內的堵塞次數，提升輸送線系統效率。

4 結語

本文提出了一種基于遺傳算法規劃環形輸送線系統的方法，并針對環形輸送線系統的瓶頸進行分析。通過對系統進行分析，得出適應度函數，從而設計出改良單親遺傳算法。通過仿真驗證遺傳算法運用在該系統的優越性，提高了物流效率。

現代化的物流系統還有許多其他的環節，例如RGV系統、AGV系統等。這些系統的貨物調度程序均可以用遺傳算法進行優化。