一種改進的無線傳感器網絡節點定位算法研究*

（中國人民解放軍91388部隊 湛江 524022）

1 引言

文獻［7］提出了一種基于移動錨節點的定位方法，該方法根據距離未知節點最近的位置RSSI值信號最強，通過錨節點的直線軌跡與未知節點的圓形通信區域相交所得的兩弦，由兩弦的中垂線交點實現未知節點坐標求解，但是實際使用中未知節點的通信區域不一定呈理想圓形，引入加權因子求解得到弦的中點不一定是距離未知節點最近的點，從而導致誤差的產生。

文獻［8］提出了一種基于RSSI值的錨節點測量方法，該方法通過構建RSSI值與相對距離的多項式方程實現未知節點最近處的坐標位置求解，能較好避免文獻［7］算法的缺陷。該算法不足之處是只采用運動軌跡上兩個點的坐標值實現對錨節點直線軌跡方程的求解，將軌跡上某一位置點作為參考節點實現RSSI值方程的擬合求解，忽視了位置數據中的異常值［9］及GNSS系統的定位偏差［10］對求解的影響，該方法極有可能對未知節點坐標的解算帶來極大的誤差。

本文在文獻［8］的基礎上提出了一種改進的無線傳感器節點定位算法。該算法中，錨節點在未知節點的通信區域內做折線運動，處于靜止狀態的未知節點獲取到錨節點廣播的位置數據和該點位的RSSI值，通過3σ準則，對位置數據中的異常值進行剔除；采用一元線性回歸對經過異常值處理的位置數據集進行擬合處理，構建了基于折線交點的RSSI多項式模型，通過解算確定未知點在錨節點軌跡上的垂線，由兩條垂線的交點求解出未知節點的位置。

2 系統模型

2.1 RSSI值模型

本文采用無線傳感器網絡中應用較為廣泛的Shanowing模型［11～12］，即發射點距離d處的 RSSI值由下面的式（1）和（2）得出：

PT是信號發射功率；PL(do)是信號在參考距離(do)處的路徑傳播損失，do通常取值為1m；η是路徑衰減因子，取值范圍為2～5；xσ是服從高斯分布的隨機變量，其均值為0，標準差的取值范圍為4～10。

2.2 折線運動模型

為了便于未知節點坐標的求解，本文制定了錨節點的折線運動模型，具體敘述如下。

論做人地道，香娭毑在白家灣幾十年，還真是沒留話柄讓人說。平日里，不管是誰，你從她家屋門口過，她總是熱情地同你打招呼，你進來糯（坐）啦！呷拿（茶）啦！一口家鄉話十分悅耳動聽。她泡的姜鹽茶和芝麻豆子茶還真是好呷，讓人呷了一盅又一盅，舍不得放下盅哩。只可惜生不逢時，若放在當年乾隆爺下江南，呷了她的茶，這茶一定會成為貢品。大伢細崽去了她家，更討她喜歡，她會變戲法似的，一會兒給你拿顆糖，一會兒抓把炸得透香的紅薯片放到你手上，讓你覺得像過年。白家灣無論大人還是細伢子，有事冇事都喜歡往她家拱。

如圖1所示，未知節點U處于靜止狀態，虛線為U的通信半徑，K為具備定位功能（即安裝有GNSS系統）的錨節點，其接到未知節點的定位需求以后規劃路徑，在U的通信區域內做折線運動，并周期性地廣播位置信息。未知節點接收到其廣播的位置信息并獲取其在該位置的RSSI值。

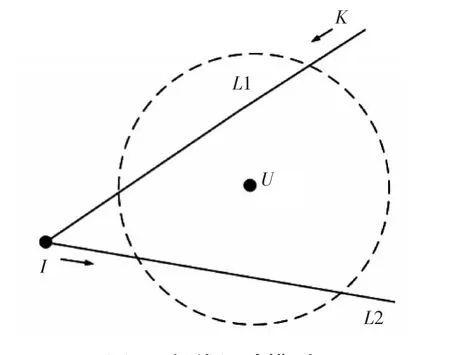
圖1 折線運動模型

2.3 基于一元線性回歸的直線軌跡方程求解模型

如圖1示，錨節點在直線軌跡L1和L2上運動時，未知節點將會分別獲得一組具有線性關系的位置數據集 (xi，yi)(i=1，2，...，n)，設直線軌跡方程為

為獲得該組數據的最佳線性關系，一元線性回歸中常采用最小二乘準則對數據進行處理，即參數a和b的值可以由式（4）和式（5）［13］得出：

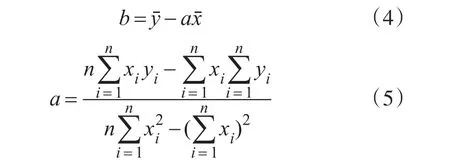
當測量數據中存在有異常值時，由于異常值會對回歸效果產生扭曲，采用最小二乘準則并不能獲得最佳線性關系。為減小測量數據中異常值對回歸效果的影響，本文采用3σ準則對異常值進行檢測和剔除［14～15］，具體步驟如下：

1）對位置數據值進行線性回歸處理，由式（4）和式（5）計算得到a和b。

2）使用貝塞爾公式，即式（6）計算該組數據的標準差s：

3）使用3σ準則，即式（7）對每組位置數據進行判斷。如式（7）成立，則待檢測的yi為異常值予以剔除。

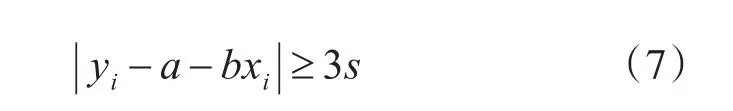
4）對余下的位置數據重復步驟1）、2）和3），直至剔除所有異常值，最后由式（4）和式（5）求解得到直線的軌跡方程。

2.4 基于折線交點的RSSI值多項式模型

如圖2所示，I點為直線軌跡L1和L2的交點，A點和B點為L1與未知節點通信區域的交點，C點為未知節點U在直線L1上的垂點。將交點I作為參考節點，直線軌跡上的其他點與交點間的距離作為相對距離。由RSSI值模型可知，距離未知節點越近的地方，信號強度越強，錨節點從A點經C點運動至B點的過程中時，未知節點獲取到的RSSI值變化趨勢如圖3示。

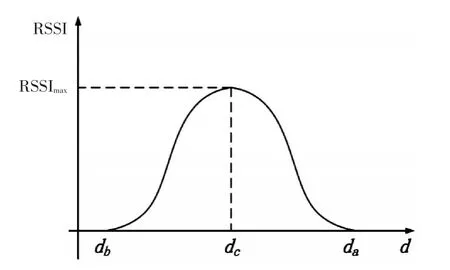
圖3 RSSI與相對距離d的關系圖

為求解出軌跡L1最大值RSSI值點處的相對距離dC，本文采用文獻［8］的方法，分別對軌跡AC和軌跡CB段的RSSI值和相對距離d進行曲線擬合，可以得到以相對距離d為自變量的擬合方程（8）和式（9）［8］：

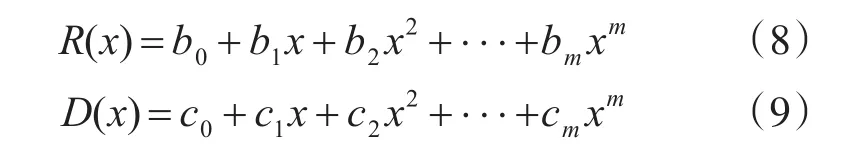
其中，R（x）和D（x）分別直線段軌跡AC和CB段的RSSI值多項式方程，聯立式（10）和式（11）求交點，由式（12）可求解得到L1直線段軌跡上最大RSSI值處的相對距離dC：

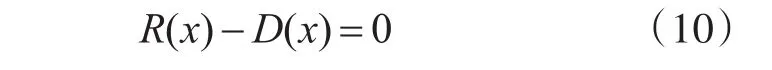
同理可以求解得到直線軌跡L2上最大RSSI值處的相對距離。

2.5 基于最大RSSI值的定位模型

同一平面內，過直線上或直線外的一點，有且只有一條直線和已知直線垂直。未知節點獲得兩條不同直線軌跡上的最大RSSI值點的位置坐標，求解得到過該點且垂直于直線軌跡的垂線，兩垂線的交點即為所求的未知節點。

如圖 4所示，點C1(cx1，cy1)，C2(cx2，cy2)分別為錨節點直線軌跡L1和L2上的最大RSSI點；L3和L4分別U在L1和L2上的垂線。分別對直線軌跡L1和L2進行線性回歸處理得到對應的方程式（11）和式（12）：

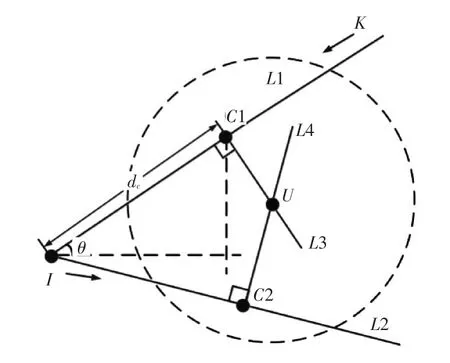
圖4 最大RSSI值的定位模型圖

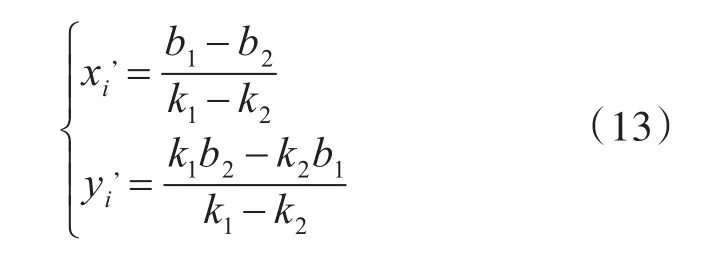
直線L3，L4分別垂直L1，L2，由幾何關系可得L3和L4的方程分別為

由式（14）和式（15）可求解得未知節點U的坐標：

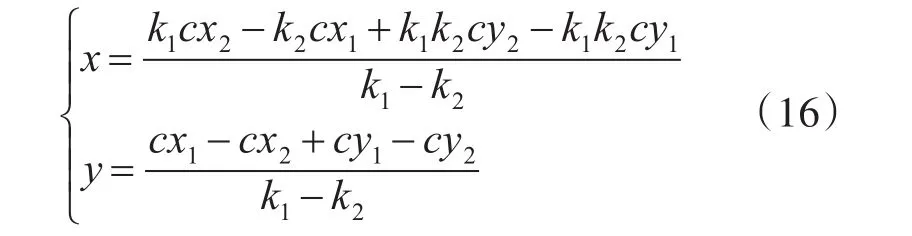
(cx1，cy1)和 (cx2，cy2)分別為垂點C1和C2的坐標，由圖4可知垂點坐標：

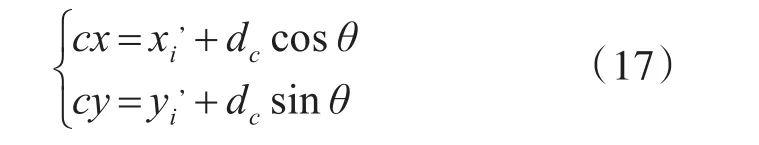
其中，θ=arc(tank)，聯立式（4）、式（5）、式（13）、式（16）和式（17）可解得未知節點的坐標。對未知節點的坐標公式分析可以得知：

1）由式（4）、式（5）、式（13）、式（16）和式（17）的推導過程可知，未知節點坐標的解算精度最終受到錨節點的位置誤差和位置數據樣本量n的影響。

2）k1≠k2，即執行折線運動過程中，兩條直線段不能重合或者平行，否則將導致算法無解。

3 仿真實驗

為驗證GNSS系統的定位誤差和位置數據集的樣本量n對未知節點坐標解算的影響，本文采用Matlab軟件對算法進行了仿真分析，仿真參數設置如下：Pt=1W，η取值為1，Xσ的標準差取值為5。

無線傳感器網絡的場景設定如下：在40m*40m的矩形監測區域內，隨機布放10個固定節點，錨節點規劃路徑在監測區域內運動。為保證仿真結果的準確性，將10次獨立仿真結果的平均值作為最終結果。分別采用本文的算法、文獻［7］和文獻［8］的算法進行比較。相關的仿真結果如圖5和圖6所示。

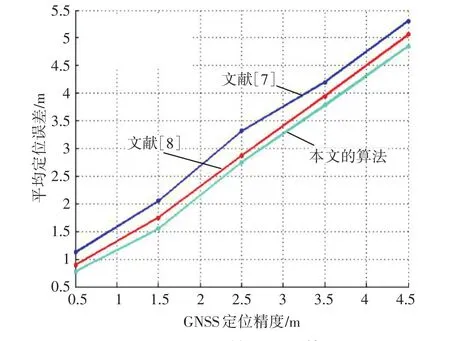
圖5 GNSS定位精度對解算影響

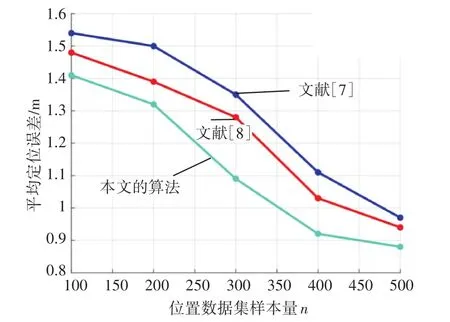
圖6 位置數據樣本量n對解算精度影響

從圖5可以看出，在相同的GNSS定位誤差下，本文的算法明顯高于其他兩種算法，這是因為首先本文的算法引入了3σ準則對位置數據集中的異常值進行剔除，其次，構建了直線軌跡方程求解模型和RSSI值多項式模型有效降低了GNSS定位誤差對后續求解的影響。第三，與原方法簡單的采用軌跡上某一位置點作為參考節點相比，本文采用折線交點作為參考節點較原算法更為精確，擬合得到的RSSI方程也較原算法更符合理論值。因此本文算法的定位精度較其他兩種算法得到了明顯的提升。

由圖6可知，樣本量n的增加，三種算法的定位誤差呈現出逐漸減小的趨勢。這是因為在相同的測量條件下，測量次數越多，越能減小隨機誤差對測量數據的影響［13］。在相同的位置數據集樣本量n下，本文的算法誤差明顯小于其他兩種算法，證明本文采用的異常值剔除方法和兩次回歸擬合運算有效減小了異常值和GNSS定位偏差對未知節點坐標解算的影響。

4 結語

本文提出了一種改進的無線傳感器網絡節點定位算法，該算法最低只需要一個錨節點就能實現未知節點的定位，算法無需附加額外的硬件設備，使用成本低廉；構建的直線軌跡求解模型和RSSI值多項式模型簡單易于實現；仿真實驗表明：與原算法相比本文的方法有效減小了錨節點GNSS系統的定位數據誤差對未知節點坐標解算的影響，具備較高的應用價值。