廣義Hietarinta-type方程的多lump解

袁 娜

(重慶電子工程職業學院，重慶 401331)

近年來，隨著符號計算的發展[1-5]，人們開始關注lump解的相關理論。2015年，馬文秀[6]提出了一種直接用Hirota雙線性方法求lump解的方法，并給出了理論證明和推導，將lump解的研究推向了一個新的階段。目前，許多研究者已經用這種方法成功地構造了多個高維非線性發展方程的lump解和相互作用解。這些解的研究對于數學、物理等領域的許多高維非線性問題具有重要的意義和前景。隨后扎其勞教授將相關理論推廣到了求可積方程的多lump解[7]。進一步豐富了lump解的相關理論[8]。

我們研究如下廣義Hietarinta-type方程

γ1uyt+γ5uyy+γ3uxt+α2(3ututt+3vttuxt+uxttt)+γ4uxy+(γ2+6α1ux)uxx+α1uxxxx=0

(1)

其中u=u(x,y,z,t)=vxt=vxt(x,y,z,t)，α1，α2和γi(i=1,…,5)都是任意常數。α2反映了Hietarinta-type非線性項[9]。這個非線性項得存在導致了相應的Hirota雙線性方程解中的常數項非常復雜。馬文秀教授[6]構建了方程(1)的Hirota雙線性形式，并且證明了一個Hietarinta-type四階非線性項可以產生具有二階線性色散項的lump解。然而到目前為止，廣義Hietarinta-type方程的多lump解尚未有文獻進行討論。本文基于馬文秀教授的工作，進一步研究廣義Hietarinta-type方程的多lump解。

1 Hirota雙線性形式

利用下列對數變換

u=2(lnf)x,v=2lnf

(2)

方程(1)有如下形式的Hirota雙線性形式

(3)

其中

DyDt=2(ffyt-ftfy)

DxDt=2(ffxt-ftfx)

DxDy=2(ffyx-fxfy)

因此，方程(3)有如下等價形式

α1[ffxxxx-4fxxxfx+3(fxx)2]+α2(ffxttt-ftttfx-3ftfxtt+3fttfxt)+γ1(ffyt-ftfy)+γ2[ffxx-(fx)2]+γ3(ffxt-ftfx)+γ4(ffyx-fxfy)+γ5[ffyy-(fy)2]=0

(4)

可以證明方程(4)的解也就是方程(1)的解，這樣的話我們只需要求方程(4)的解，然后代入對數變換(2)就可以獲得方程(1)的解。

2 多lump解

為了獲得方程(1)的多lump解，做變換

f(x,y,t)=f(ρ,y),ρ=x-ωt

(5)

此時方程(4)變為

-γ5(fy)2+ωγ1fyfρ-γ4fyfρ-γ2(fρ)2+ωγ3(fρ)2+3α1(fρρ)2-3ω3α2(fρρ)2-4α1fρfρρρ+4ω3α2fρfρρρ+f(γ5fyy-ωγ1fρy+γ4fρy+(γ2-ωγ3)fρρ+(α1-ω3α2)fρρρρ)=0

(6)

首先，我們來討論方程(4)的1階lump解，使用待定系數法，假設

f(ρ,y)=(-μ+ρ)2+θ0+(y-ν)2θ1

(7)

其中μ和ν是任意常數。將(7)代入(6)，提取ρ2，y2,ρy，ρ，y的系數令為零，可得

(8)

此時可得

(9)

將(9)代入變換(2)，可得方程(1)的1階lump解

(10)

其中γi(i=1,…,5)，μ，ν是自由常數。

為了觀察解(10)的動力學性質，我們可以取

γ1=α1=1,γ2=γ5=-1,γ3=γ4=μ=ν=0

將這些參數的值代入方程(10)，利用Mathematica軟件，可得相應的三維圖形和等高線圖(見圖1)。

同理，我們假設三階lump解為如下表達式

f(ρ,y)=ρ6+θ10ρ4+θ11ρ4y2+(θ12+θ13y2+θ14y4)ρ2+θ15y2+θ16y4+θ17y6+θ18+2ρy(θ19+θ20y2+θ21ρ2)+2μυ(θ22+θ23y2+θ24ρ2)+ν2+μ2

(11)

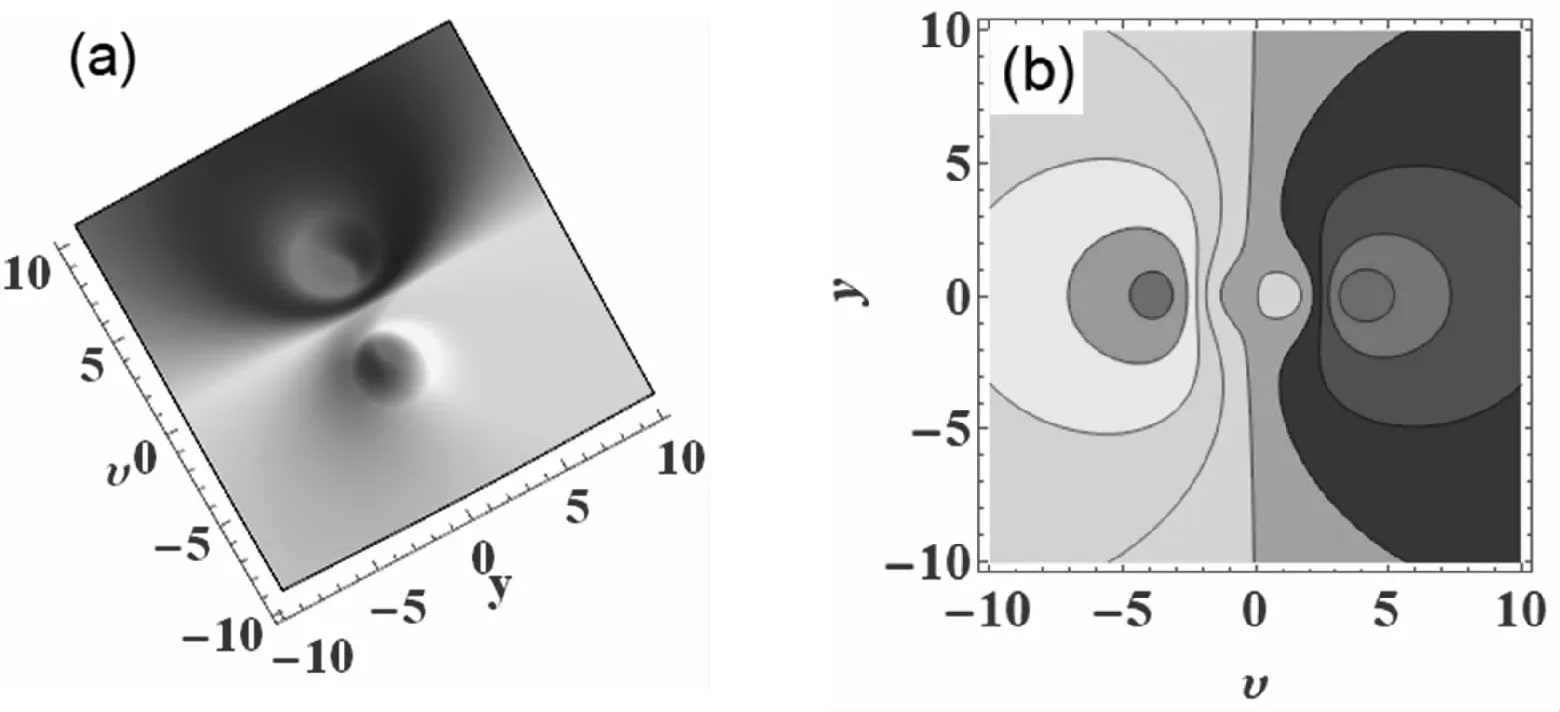
圖1 圖中υ=ρ,(a)三維圖形；(b)等高線圖形

其中θi(i=10,11,…,24)是任意常數。將(11)代入(6)，提取ρ和y的各階次冪和混合項系數令為零，可得

(12)

其中θ19和θ22是自由參數值。將(11)和(12)代入變換(2)，我們有

u(ρ,y)=2(lnf)ρ

(13)

為了觀察三階lump解(13)的動力學性質，我們可以取

γ1=α1=θ22=1,γ2=γ5=θ19=-1,γ3=γ4=0,μ=ν=10

將這些參數的值代入方程(10)，可得

u(ρ,y)=(4(10-12yυ+3y4υ+6y2(5+15υ+υ3)+υ(-125+υ(-30+50υ+3υ3))))/(1979+4y3+y6-4y(5+3υ2)+y4(17+3υ2)+y2(475+3υ(20+30υ+υ3))+υ(20+υ(-125+υ(-20+25υ+υ3))))

利用Mathematica軟件，可得相應的三維圖形和等高線圖(見圖2)。從圖2中很容易看到三個一階lump解。

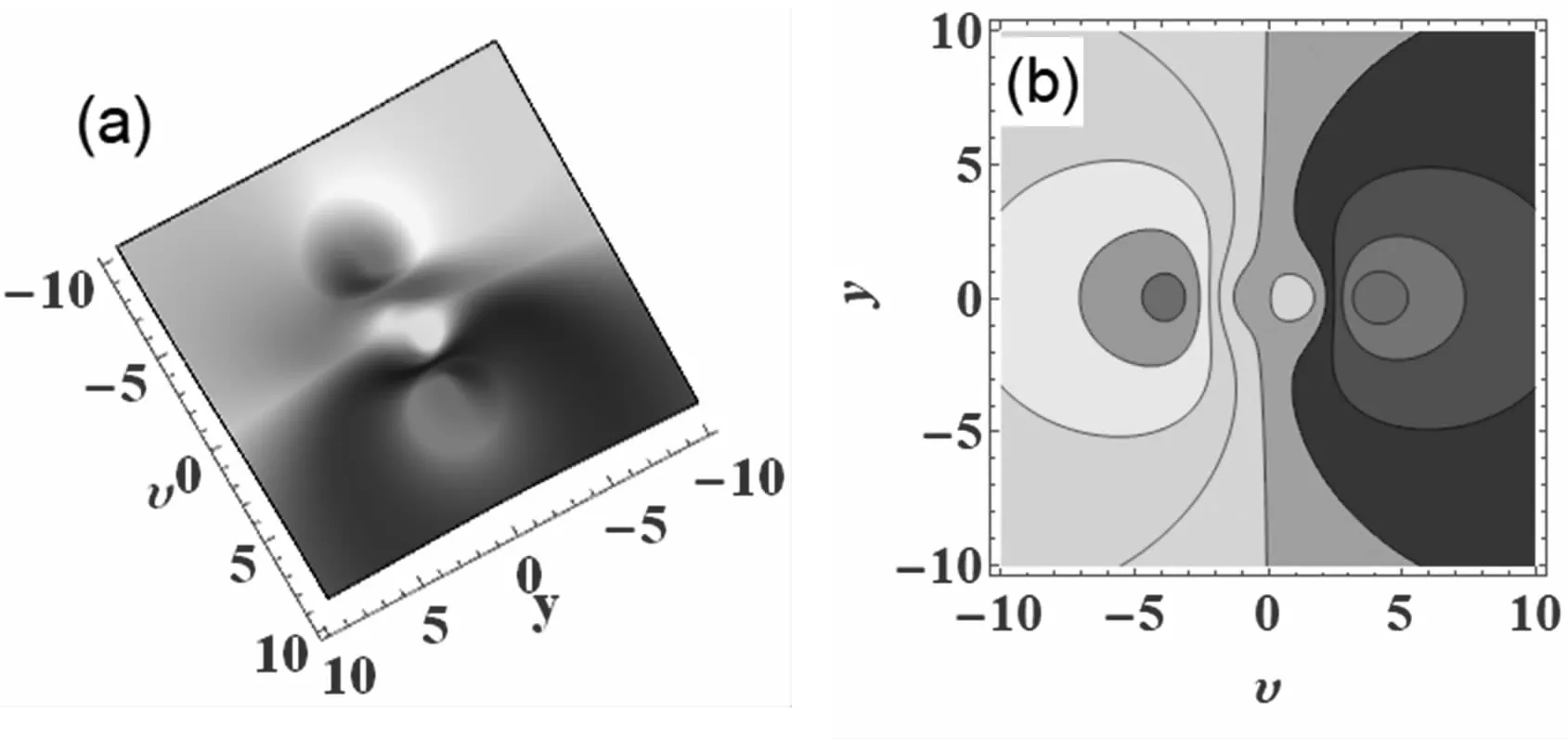
圖2 圖中υ=ρ,(a)三維圖形；(b)等高線圖形

最后，我們假設六階lump解為如下表達式

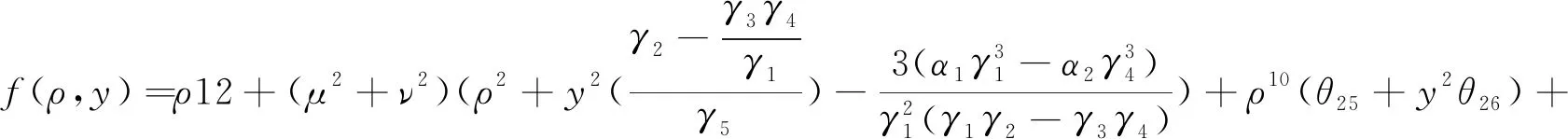
(14)

其中θi(i=25,26,…,69)是任意參數。將(14)代入(6)，提取ρ和y的各階次冪和混合項系數令為零，可得

(15)

將(14)和(15)代入變換(2)，我們有

u(ρ,y)=2(lnf)ρ

(16)

為了觀察六階lump解(16)的動力學性質，我們可以取

γ1=γ4=1,γ2=-1,γ3=α2=2,γ5=-1,α1=3,μ=ν=10 000

將這些參數的值代入方程(16)，利用Mathematica軟件，可得相應的三維圖形和等高線圖(見圖3)。從圖3中很容易看到六個一階lump解。

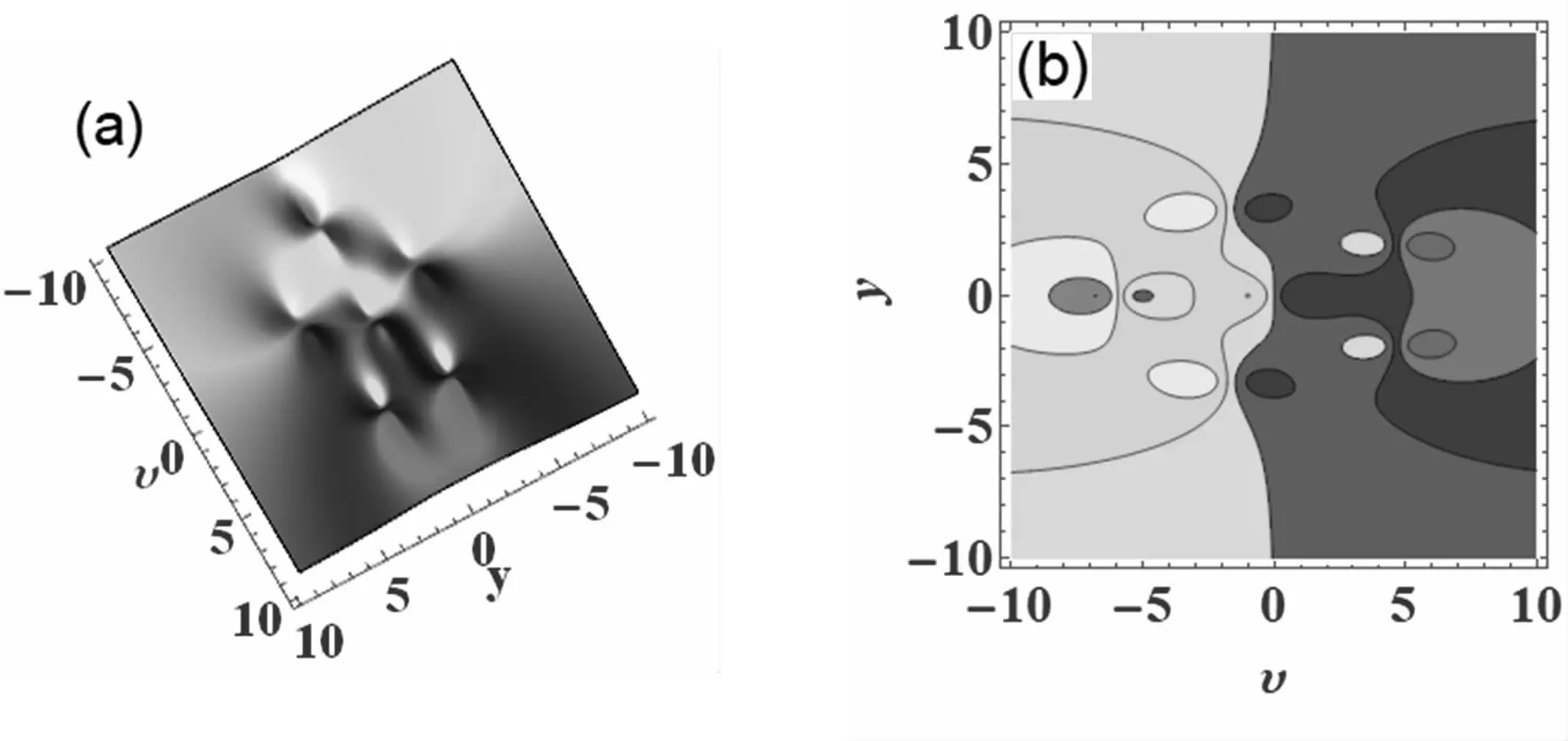
圖3 圖中υ=ρ,(a)三維圖形；(b)等高線圖形

3 總結

本文基于扎其勞教授提出的方法和馬文秀教授獲得的Hirota雙線性形式，調查了了廣義Hietarinta-type方程的多lump解，主要是一階lump解，三階lump解和六階lump解。設置一些特定參數的值，一階lump解，三階lump解和六階lump解的動力學性質分別被展示在圖1，圖2和圖3中。這些解和動力學性質尚未在其他文獻中看到。