含柔性腹節的仿蠶機器人轉彎運動建模與實驗

馬林坡，潘雪熒，王永娟，范麗萍

(1.南京理工大學 機械工程學院， 南京 210094； 2.蘇州長風航空電子有限公司， 江蘇 蘇州 215151；3.江蘇省海門中等專業學校， 江蘇 南通 226100)

仿生機器人是指模仿生物、從事生物特點工作的機器人。在生物界中，存在著許多依靠自身的身體變形波傳導來獲得有效運動能力的動物，由于其特殊的運動模式和多自由度的身體結構，它們具有很強的運動穩定性和環境適應性。目前，仿生蠕動技術的研究已經成為當前仿生機器人領域研究的熱點之一[1]。

仿生蠕動機器人具有接觸面積大、離散性高的特點，使得對坑洼等地形具有更強的適應性和穩定性[2]。連續型的關節結構和偏低的重心幫助其適應多樣性的環境。

Wright等[3]設計了一種仿蛇機器人，通過模擬蛇的運動步態，其可以實現爬行、攀爬和滾動等多步態運動，并利用頭部模塊安裝的高清攝像頭執行偵察任務。McKenna等[4]設計了一種基于環形皮膚致動器的仿蛇機器人，其利用機器人整個皮膚表面提供連續推進力，可以顯著的提高蛇形機器人在不同環境中的靈活性。Barry A.Trimmer[5]實驗室研發的仿生毛蟲機器人既可以以蠕蟲形態爬行，還可以模仿出卡特彼勒的滾動。魏武等[6]設計一種仿蛇機器人，其采用正交關節的模塊化方式連接，可通過電機的驅動實現蜿蜒爬行、轉向、抬頭等多種運動方式。

仿蠶機器人是由多個關節模塊組成的高冗余度系統，能夠適應復雜多變的環境。本文對小型仿蠶機器人的關鍵組件—柔性腹節驅動器，進行了機械結構設計、轉彎運動建模計算、仿真分析，并通過實驗驗證其合理性，為仿蠶機器人的柔性化研究奠定了基礎。

1 蠶的生物特征與仿生結構設計

1.1 蠶的生物特征

蠶的身體形態如圖1所示，生理特征參數如表1所示。蠶的頭部引導自身運動；蠶的胸部輔助自身運動，且每個體節腹面有一對胸足，胸部各體節間無節間膜。蠶的腹部輔助自身運動，后半部分4個體節的腹面有四對腹足，腹部各體節間有節間膜。蠶的尾部作為自身運動的動力源，末尾體節的腹面有一對尾足，尾部各體節間有節間膜。

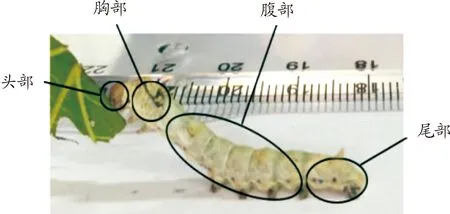
圖1 蠶的身體形態示意圖

表1 蠶的生理特征參數

蠶依靠胸部與腹部連接之間無腹足的柔性腹節單側肌肉的收縮與伸展來完成轉彎動作，如圖2所示。蠶腹部各體節間有節間膜，但柔性腹節處無腹足，且相比于其他關節，運動變形較大且靈活，具有分布式連續變形的能力。

圖2 蠶的轉彎運動示意圖

1.2 柔性腹節驅動器的結構設計

根據蠶的生物結構和轉彎運動特點進行機構簡化，采用模塊化設計[7]。的仿蠶機器人的整體結構模型如圖3所示，基本分為頭部，腹部、尾部3個部分，其中頭部主要起導向作用，腹部作為轉彎運動動力源，尾部作為蠕動運動動力源。仿蠶機器人全長720 mm，寬56 mm，每節體節長約61 mm，共由11節組成，各體節之間采取正交連接的方式，構成4個正交模塊，每個正交模塊中由俯仰關節和偏航關節組成，俯仰關節完成蠕動動作，偏航關節完成轉彎動作。

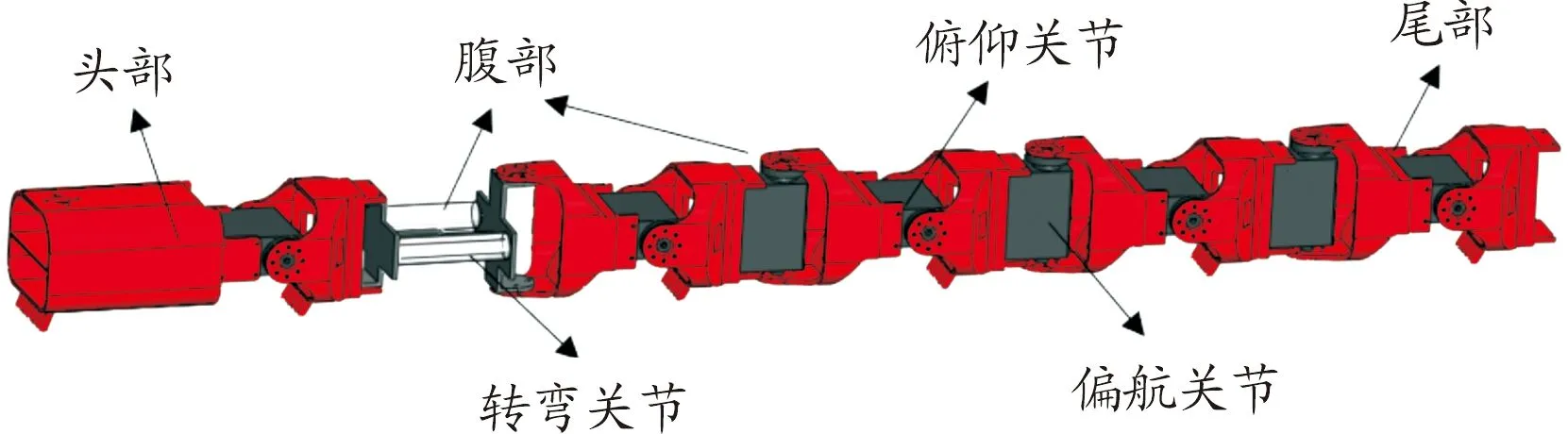
圖3 仿蠶機器人整體結構示意圖

為實現仿蠶機器人轉彎關節的柔性化，增強其環境適應能力[8]，基于蠶腹部前半部分的結構特點和運動特性設計柔性腹節驅動器，如圖3中轉彎關節所示。柔性腹節驅動器是一種差動式的關節驅動器[9]，如圖4(a)所示，分別進行兩側氣囊的充氣，將單側氣囊輸出的直線位移轉換成關節的角位移，從而實現往復的擺動運動。

圖4 驅動器工作原理及數學模型

如圖4(b)所示，柔性腹節驅動器中單個剛體連桿的長度為l，氣囊偏心距為a，假設單側氣囊伸長的長度為X時，驅動器的轉動角度為θ。

連桿轉角α=π-θ/2，氣囊彎曲角度β=π/2-α=θ/2，則氣囊的伸長長度為

(1)

氣囊的形變量為

(2)

通過MATLAB對式(2)進行計算，得到氣囊形變量與其彎曲角度的關系如圖5所示，可以看出氣囊的有效轉彎角度為45°，最大伸長量為7.7 mm。

柔性腹節驅動器的主體是由兩個硅橡膠制作的氣囊組成，氣囊由圓柱形的氣囊空腔和菱形固定支架組成[10]，氣囊的結構設計如圖6所示。氣囊整體長度為54 mm，內壁直徑為6 mm，壁厚為3 mm，兩側的菱形支架安裝在驅動器的支撐架上。當進行轉彎運動時，氣囊充氣后開始膨脹發生軸向和徑向位移，但由于固定支架的限制，徑向位移對運動幾乎沒有影響，可以忽略不計，主要利用其軸向上的位移。

圖6 氣囊結構

2 仿蠶機器人轉彎運動建模與仿真

2.1 轉彎運動曲線及其規劃

為了方便建立仿蠶機器人轉彎運動模型，將其簡化為二維平面連桿系統，用連桿形成的運動波來模擬機器人的轉彎運動[11]。當仿蠶機器人進行轉彎運動時，以轉彎關節運動導向為主，偏航關節的轉動為輔。含有柔性腹節驅動器的轉彎關節的轉角變化規律如下：

φ(t)=Asin(ωt+λ)

(3)

式中:A為幅值參數;ω為轉動角頻率;λ為偏轉參數。

偏航關節的轉角變化規律可以采用Serpenoid曲線[12]來規劃輔助轉彎運動軌跡，可以參考Serpenoid曲線對偏航關節的轉彎運動進行規劃[13]。

(4)

首先將Serpenoid曲線的曲率方程進行簡化[14]

ρ(s)=-absin(bs)+c

(5)

對式(5)進行積分運算，得到夾角θ(s)

θ(s)=acos(bs)+cs

(6)

為了方便得到仿蠶機器人的轉彎運動方程，將其簡化為N節平面連桿，當連桿長l足夠小時，連桿連接就可以近似為光滑的轉彎曲線，對于仿蠶機器人的N節連桿，其關節轉角即為弧長s=0，l，2l，…處的夾角。經過計算，最后得到弧長s=ct，ct+l，ct+2l，…的關節轉角函數為

φi(t)=αsin(ωt+(i-1)β)+γ

(7)

其中：α為轉彎曲線的初始角度，主要影響曲線的幅值，β決定關節間的相位差，主要影響運動曲線中包含波的數目，ω決定轉角頻率，主要影響曲線周期。

為了提高轉彎運動控制函數基于仿蠶機器人轉彎運動的實際應用性，通過單位階躍函數g(t)=1-e-λt對其進行優化，使信號更加平滑地進入系統。g(t)函數的曲線如圖7所示，令λ分別取值為0.5、1、2、3，從其中可以看出，λ數值越大，函數增長越快，響應時間越短。因此可以使用該函數對轉彎運動控制函數進行優化，優化后的函數如式(8)所示。

φ(i)=(1-e-λt)(asin(ωt+(i-1)β)+γ)

(8)

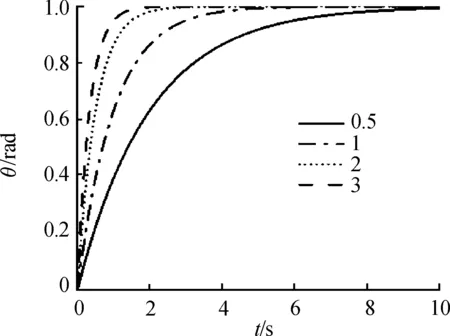
圖7 λ參數對單位階躍函數的影響曲線

取參數a=π/6，β=0.6π，ω=2，γ=0，然后分別取λ=0.5、1、2、3，根據式(8)可得偏航關節在不同值下的角度變化曲線，如圖8所示，數值越大，函數到達期望角度越快，通過g(t)函數優化的意義是希望角度可以平滑地從0增長到期望值，從而保證轉彎運動控制函數的實用性和穩定性，因此選取λ=0.5作為函數參數。

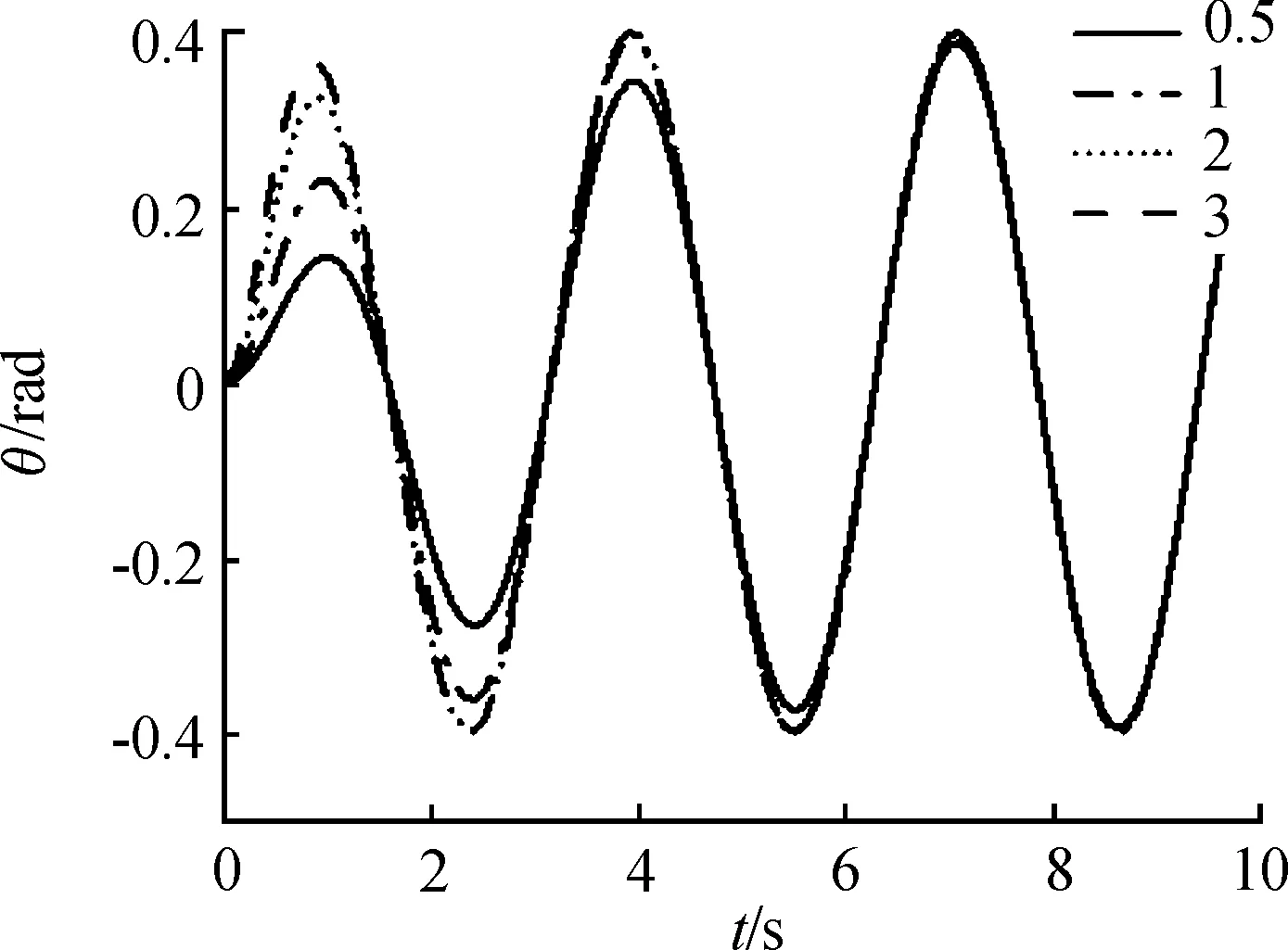
圖8 λ參數對轉彎運動控制函數的影響曲線

最后，得到仿蠶機器人轉彎運動控制函數如式(9)所示，i=1時，表示的轉彎關節，i=2、3、4時，表示的是偏航關節。

(9)

2.2 轉彎運動分析與仿真

為了驗證基于柔性腹節驅動器建立的轉彎運動控制函數的可行性，對仿蠶機器人進行基于ADAMS轉彎步態仿真。

在上面小節，建立了轉彎運動控制函數，其中，參數γ影響的是轉彎運動的方向。此時，偏航關節起輔助轉彎運動的作用，其運動軌跡不發生偏轉，因此γ=0。仿蠶機器人的轉彎運動控制函數如下所示。

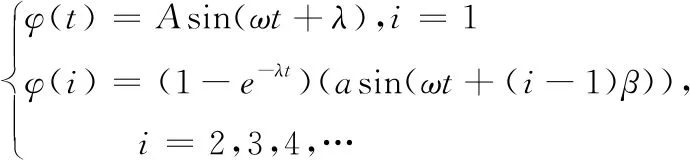
(10)

在ADAMS中搭建仿真平臺，根據期望的轉彎角度，取a=π/6，β=0.6π，ω=2，λ=0.5。設置仿真時長為40 s。仿蠶機器人右轉彎運動仿真過程如圖9所示。

圖9 一個周期的轉彎運動仿真過程示意圖

其中參數ω主要影響的是轉彎運動的周期，α影響曲線的幅值，β決定關節間的相位差，從而影響轉彎運動的速度。通過仿真分析，得到小型仿蠶機器人轉彎運動時的偏航關節的角度變化的關系，如圖10所示。

仿蠶機器人頭部在x軸方向的角度變化如圖11所示，從圖11中可以看出含柔性腹節的仿蠶機器人在轉彎運動開始時，頭部轉角有輕微抖動，但逐漸趨于平緩，直至達到穩定狀態。由此可以證明依靠頭部進行導向運動，偏航關節進行輔助運動的轉彎模型，可以使仿蠶機器人的轉彎運動趨于平滑穩定。

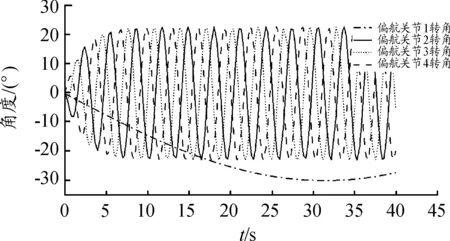
圖10 關節角度變化圖

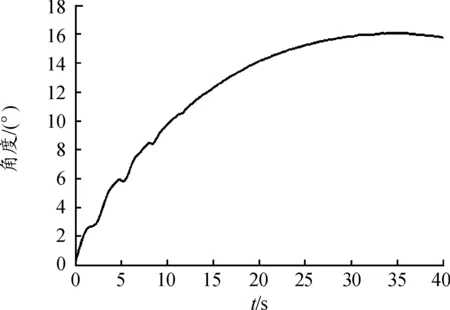
圖11 轉彎角度變化曲線

3 基于ADAMS和MATLAB的轉彎關節聯合仿真

由于存在柔性腹節驅動器自身的非線性特性和氣泵電磁閥開關操作延遲的影響，會導致仿蠶機器人在進行轉彎運動時關節擺角出現累計偏差，致使關節擺角脫離期望的運動軌跡，因此，通過ADAMS和MATLAB聯合仿真技術，運用數字PID控制方法，解決這一非線性問題。

3.1 聯合仿真虛擬樣機系統的設計

通過基于ADAMS和MATLAB的轉彎關節聯合仿真，主要分為4個步驟，如圖12所示。

圖12 聯合仿真流程框圖

首先建立仿蠶機器人機械結構的虛擬樣機模型，定義各模塊構件間的約束和驅動相關屬性，添加合適的分量力矩；然后在MATLAB中設計并搭建仿蠶機器人進行轉彎運動的控制方案；最后進行仿真和調試，通過設置數據交換時間間隔、仿真時間和步長，最終得到關節角度變化曲線圖。

3.2 基于PID控制算法的控制器設計

仿蠶機器人的轉彎關節的PID控制器是以數字式PID控制算法為理論基礎，在控制程序中，其入口參數為期望角度值和實際角度值，期望角度就是控制給出的角度值，反饋角度是傳感器測得的驅動器的轉彎角度[15]。

如圖13所示，上位機設置期望角度，測量角度來自MPU6050，期望角度減去測量角度得到偏差角度，角度環的輸入為偏差角度值，經過角度環PID后輸出期望的角速度[16]，更新周期100 Hz。

圖13 PID算法流程框圖

根據含有柔性腹節的仿蠶機器人轉彎運動模型，在MATLAB/Simulink中建立仿蠶機器人轉彎關節的PID控制器的仿真模型。

3.3 聯合仿真結果分析

基于ADAMS和MATLAB的聯合仿真方法對仿蠶機器人柔性腹節的轉彎運動擺角偏差進行修正，并對擺角進行實時跟蹤與控制。在仿真的過程中，根據PID控制器的調參公式不斷修改控制器的3個參數，直到角度變化的軌跡為比較理想的曲線。

設置仿真時間為6 s，擺角的期望值為20°，多次調整3個參數后得到較為理想的轉彎運動擺角曲線如圖14。

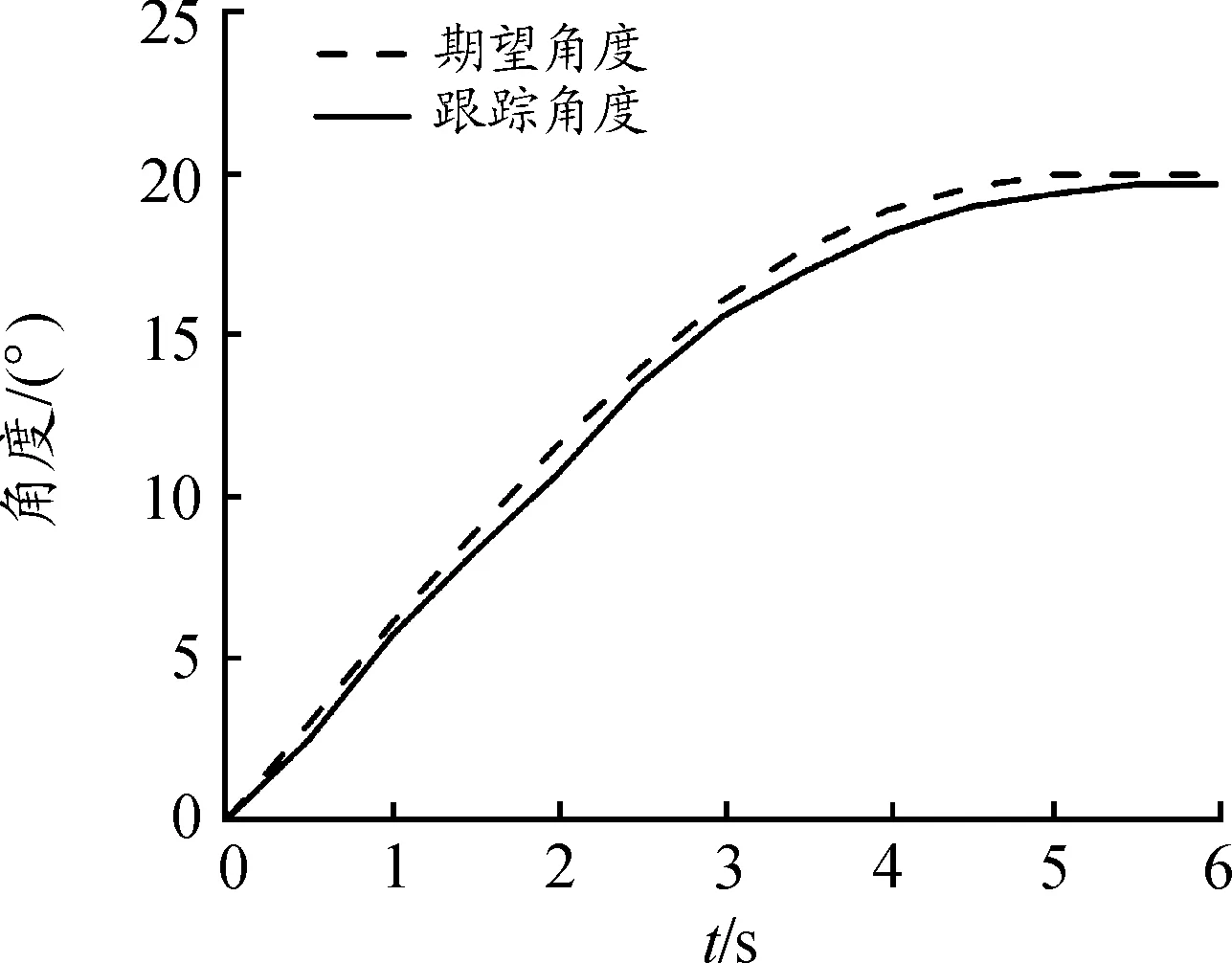
圖14 角度跟蹤曲線

當比例環節系數KP=0.023、積分環節系數KI=0.041、微分環節系數KD=1時，可以得到較為理想的角度變化軌跡曲線，角度過渡平緩，穩定性好。

4 轉彎運動試驗

對仿蠶機器人進行零部件安裝與調試，仿蠶機器人初始狀態如圖15(a)所示，左轉彎效果如圖15(b)所示，右轉彎過程如圖15(c)所示。

轉彎運動的仿真結果與機器人樣機的試驗結果如圖16所示，其中兩條曲線分別表示在轉彎運動仿真與機器人樣機試驗中機器人頭部在x軸方向的角度變化。從圖16中可以看出，給定的預期轉彎角度為16°，實際轉彎角度達到了15°，經過ADAMS和MATLAB轉彎關節的聯合仿真，由于引入了PID控制算法，在進行轉彎運動時，頭部的轉彎角度在起始位置運動比較穩定，然后慢慢穩定的平滑轉動到期望轉彎角度，滿足本項目要求仿蠶機器人轉彎運動自然、過渡柔順化的要求，試驗結果基本符合預期。

圖15 左右轉彎效果圖

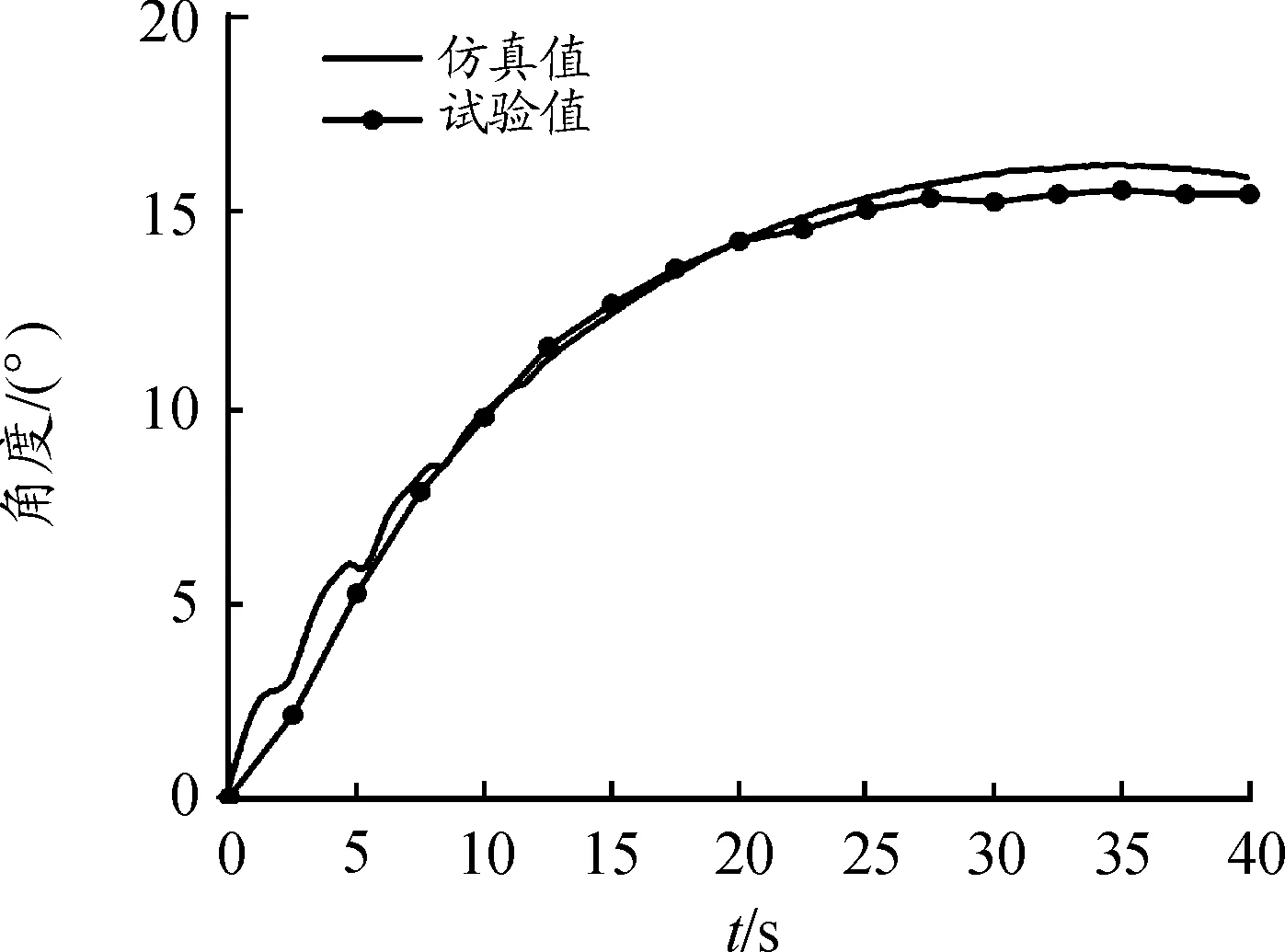
圖16 轉彎角度曲線

5 結論

1) 建立了仿蠶機器人簡化連桿轉彎運動模型及其轉彎運動模型控制函數，通過ADAMS仿真驗證了轉彎運動模型的合理性及其控制函數的實應性。

2) 通過樣機試驗了仿蠶機器人的轉彎運動控制模型，驗證了柔性腹節驅動器設計的可行性，對仿蠶機器人的柔性化研究具有重要參考價值。