基于Bagging-CNN雷達信號分類方法

孫藝聰，田潤瀾，劉 沖，郭 揚

(1.空軍航空大學航空作戰勤務學院， 長春 130022； 2.空軍參謀部電子對抗雷達局， 北京 100000；3.空軍航空大學教研保障中心， 長春 130022)

對于電磁環境日益復雜的今天，如何快速準確地對未知雷達信號進行分類和識別，一直是信號處理領域的重點研究方向，尤其是在軍事對抗中，能夠快速對未知信號進行分類識別，對后續的戰爭行動有著深遠的影響[1-2]。圍繞著雷達信號識別與分類的問題上，國內外研究人員進行了大量的研究。文獻[3]提出了一種基于時頻圖像的雷達波形識別系統，能夠識別多種波形。文獻[4]提出了一種基于時頻圖像預處理下卷積網絡雷達信號識別方法，相比人工提取特征的準確率有所提高。文獻[5]提出了一種基于積分旋轉因子的徑向積分方法，在時頻圖像的基礎上對信號進行檢測。文獻[6]提出了一種基于卷積神經網絡和平均采樣技術的信號自動識別方法，有效降低了處理信號時所需的大量計算成本。文獻[7]采用了特征融合和支持向量機的方法，具有較好的準確性和魯棒性。文獻[8]提出了一種基于短時傅里葉變換與卷積神經網絡的分類方法，具有較高的識別性能。但是上述方法在低信噪比情況下識別準確率有限，且不同類型信號之間識別準確率也有一定的差距，訓練得到的網絡具有一定的偏向性，這就會導致特征明顯的信號類型更容易被識別出來，而特征不明顯的信號類型更容易被判錯，不利于后續的分析處理。

為了改善上述問題，本文提出一種雷達信號分類方法，首先利用卷積神經網絡(convolutional neural network，CNN)提取圖像的特征，得到初步的分類結果，然后利用Bagging集成方法對CNN得到的結果進行集成決策，減少CNN網絡帶來的方差。本文首先介紹了特征提取方法和圖像預處理方法，接著介紹了Bagging框架和CNN的基本知識以及網絡結構，然后設計了Bagging-CNN分類方法的實現流程，最后設計了仿真實驗。實驗結果表明，本文提出的方法相比于傳統的神經網絡方法整體識別效果更好，在低信噪比情況下也展現了較好的分類能力，同時類別之間的差距也有所減少。

1 特征提取及圖像預處理

1.1 模糊函數特征提取

不同調制方式的雷達信號在分辨力、精度、模糊度等方面有著不同的表現，體現在模糊函數上的形式也有所不同。模糊函數在雷達信號分析方面有著很重要的作用[9]，在雷達波形設計中，也常用模糊函數作為設計工具[10]。模糊函數的一般定義為：

(1)

式(1)中：τ表示時間延遲：fd表示多普勒頻移：x(t)表示信號的復包絡。

模糊函數具有許多重要的性質[11]：

1) 唯一性。對于任意給定的信號，它都有唯一的模糊函數，不同信號有不同的模糊函數。

2) 原點對稱性。

|χ(τ，fd)|=|χ(-τ，-fd)|

(2)

3) 體積不變性。體積不變性也叫作模糊原理。它表示模糊函數圖中曲面下體積只取決于信號的總能量。

(3)

根據這些不同，可以將模糊函數圖像作為神經網絡的輸入圖像特征。由于模糊函數圖是三維立體圖，為了使其能夠作為神經網絡輸入數據，需要進一步處理為二維平面圖[12]。本文主要選用5種信號類型，分別為BPSK、Costas、FMCW、Frank和P4，以各個類型信號的模糊函數的等高線圖作為輸入特征，如圖1所示。

圖1 5種雷達信號模糊函數等高線圖

1.2 數據集的預處理

在對神經網絡訓練之前，首先對要訓練的數據集進行預處理，以減少卷積神經網絡輸入的數據量，同時對數據進行增強，以保留足夠多的特征用于后續分類工作的影響，提高神經網絡的準確率和訓練效率。本文采用圖像閾值處理對圖像進行預處理。

圖像閾值處理是一種常用的圖像處理方法。首先將圖像灰度化，然通過一定的規則對灰度化后的圖像設置閾值，根據閾值調整像素值，將圖像二值化。根據閾值設置的不同，可以分為全局閾值和局部閾值，也可以分為單閾值和多閾值。主要的圖像閾值處理方法有以下3種：簡單閾值；Otsu’s二值化；自適應閾值。

3種閾值處理方法的主要區別在于閾值的設定上。簡單閾值是一種全局性的閾值，通過設定一個全局閾值，然后整個圖像與該閾值相比較；Otsu’s二值化適用于圖像灰度直方圖中具有雙峰的情況，通過算法在雙峰之間找到一個值作為閾值；自適應閾值相對于簡單閾值可以看作是局部性的閾值，通過規定一個一定大小的區域，比較某點與區域大小里面像素點平均值的大小來確定這個像素點是屬于黑或者白。圖2是對原始圖像分別進行簡單閾值、Otsu’s二值化和自適應閾值處理的結果，其中自適應閾值設定的區域大小為5×5。

圖2 原始圖像和3種閾值處理方法效果

2 Bagging算法和卷積神經網絡

2.1 Bagging算法

在機器學習中，主要目標是訓練一個穩定的對于每一類效果都好的網絡模型，然而實際情況下并不都是這樣。有時候我們會得到具有偏向性的模型，對于某些類的處理效果特別好，而對其他類的處理則特別差，這樣的網絡模型不適合于實際應用中。集成學習[13]思想就是通過組合一些弱模型，使其能夠優勢互補，這樣即使是某個模型預測結果是錯的，其他模型也能夠糾正過來。一般情況下，融合多個網絡的效果要優于單個網絡的效果。

集成學習在如今的許多領域都有所應用，在信用評估、價格預測、數據分析、情感分析等方面取得了不錯的效果[14-15]。常見的集成學習方法有Bagging、Boosting和Stacking等3種方法。其中Bagging算法是常用的一種框架，它通過重采樣的方法在原始訓練集中選擇自己的訓練子集，從數據集中通過有放回的抽樣得到n個子樣本集，大小同原始訓練集相同，而且每個訓練子集都是相互獨立的。由于每一個樣本抽到的概率Pi為：

Pi=1-(1-1/N)N

(4)

式(4)中：i為第i個樣本；N為樣本的總數。當N的數量足夠大時，根據極限定理可得：

1-1/e≈0.632

(5)

這意味著有63.2%的數據參與了網絡的訓練，而有36.8%的數據由于沒被選中而不參與網絡的訓練，可以用來檢驗網絡的泛化能力，而且對于原始樣本有噪聲數據時，通過重采樣，就會有1/3的噪聲樣本不會被訓練，這樣就不容易受到噪聲的影響，可以降低模型的方差。

Bagging算法的流程如圖3所示，通過圖3可以看出，Bagging框架下的個體學習器可以并行訓練，具有很高的學習效率。Bagging算法通過重采樣方法得到n個不同的訓練子集，進而訓練得到n個不同的且各自獨立的個體學習器，然后通過集成策略對這n個個體學習器的結果進行集成，得到最終的預測結果。常見的集成策略有投票法和平均法，其中Bagging算法常用的方法是投票法，分為加權投票法和多數投票法。通過集成策略得到最終的識別結果。

Bagging算法的流程如下：

輸入：樣本集D={(x1，y1)，(x2，y2)，…，(xm，ym)}，其中x為樣本，y為樣本標簽；

輸出：分類器f(x);

1 fort=1，2，…，n

(1)有放回的選取樣本得到子樣本集Dt;

(2)根據子樣本集Dt訓練得到子學習器ht;

End for

2 根據集成策略將ht結果集成得到最終分類器f(x)

Bagging算法的基學習器一般采用的是弱學習器，但是在實際中為了減少基學習器的數量，一般會采取比較強的學習器，如卷積神經網絡、支持向量機等。本文主要采用卷積神經網絡作為基學習器。

圖3 Bagging框架流程框圖

2.2 卷積神經網絡

卷積神經網絡[16-17]是一種帶有卷積結構的深度學習網絡，主要用于計算機視覺和自然語言處理領域。一般常見的卷積神經網絡主要由輸入層、卷積層、池化層和全連接層組成，通過這些層的疊加，就可以構成一個卷積神經網絡。通常為了能夠提取深層次的特征，會采用將卷積層與池化層結合的方式，組成多個卷積-池化組，逐層提取特征信息，最終通過若干個全連接層完成分類。卷積神經網絡最大的2個特征是局部連接和權值共享。局部連接的方式可以有效地減少參數的數量，提升網絡訓練的效率，并且在一定程度上可以減小過擬合的風險；權值共享的方法可以進一步地減少參數的數量，通過相同的卷積核對圖像上的不同區域做卷積，以檢測相同特征。為了降低過擬合的影響，本文采用了2種方法來降低過擬合的影響：① 使用Dropout方法。讓每個神經元以一定的概率被舍棄，以減少隱藏節點的相互作用，增強模型的泛化能力；② 采用交叉驗證的方法。通過設置驗證集，用來驗證訓練集得到的模型的性能和指標。

本文設置輸入神經網絡輸入圖像的大小為32×32，設置3組卷積層與池化層，卷積核的大小為3×3，卷積方式為same，步長為1；池化方式采用2×2最大池化；所有中間層采用的激活函數為ReLU函數，全連接層后采用的激活函數為softmax函數。具體網絡結構如圖4所示。

3 流程設計

圖5是本文提出的信號分類方法的流程框圖。整個流程分為特征提取模塊和網絡集成模塊，其中特征提取模塊主要完成對原始雷達信號的特征提取與數據的預處理，并形成能夠輸入到分類網絡模塊的數據集；分類網絡模塊由n個結構相同的卷積神經網絡通過Bagging集成方法組合而成，主要完成對輸入特征的學習和分類。具體實現步驟如下：

步驟1 將原始雷達信號求模糊函數，并將模糊函數圖像轉換為二維圖像特征。

步驟2 將步驟1得到的二維圖像進行圖像閾值處理和形態學處理。

步驟3 將預處理后得到的圖像作為數據集，采用重采樣的方法對數據集進行采樣，得到n個新的子數據集，將這n個子數據集作為輸入對n個卷積神經網絡進行訓練，得到n個不同的基學習器。通過集成決策，將n個基學習器的學習結果進行投票決策，得到最終的分類結果。

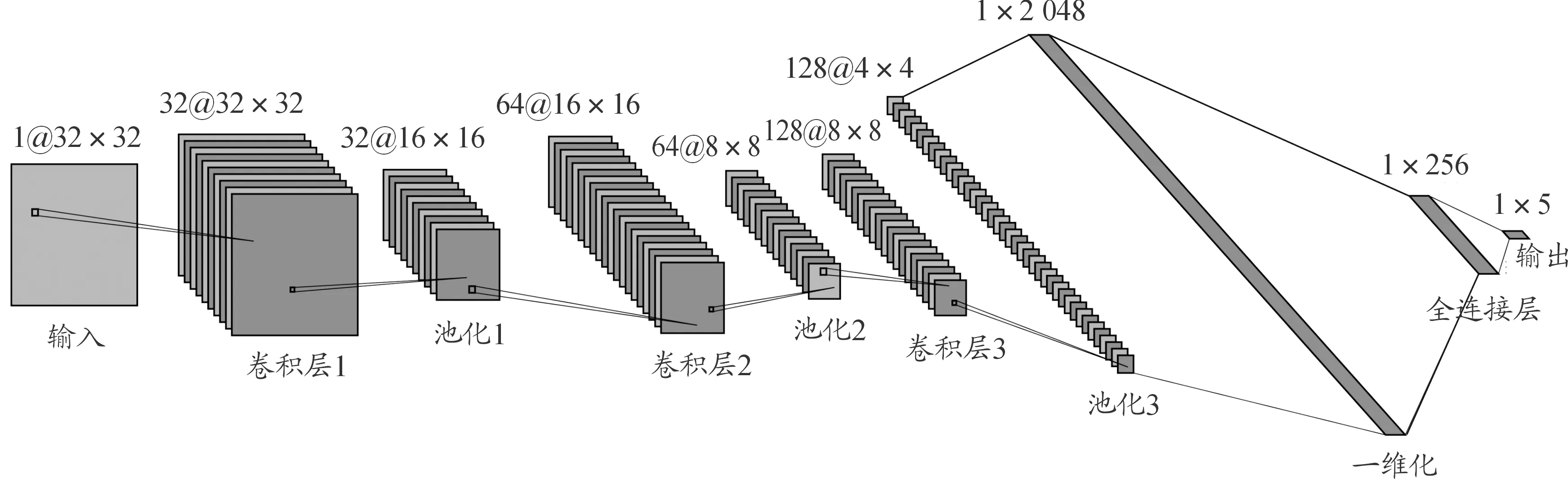
圖4 卷積神經網絡結構框圖

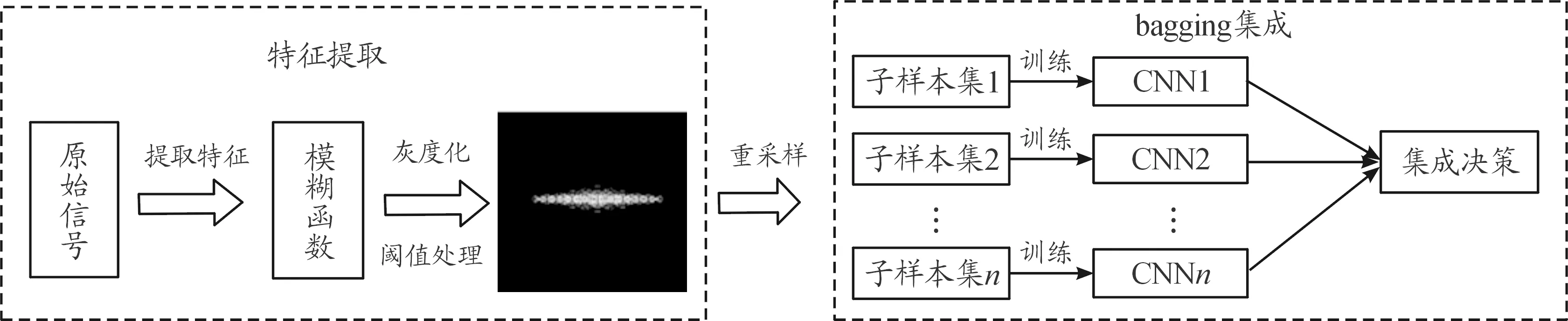
圖5 整體流程框圖

4 仿真實驗與結果分析

利用MATLAB產生仿真信號，每種信號各產生800個樣本，用于對分類網絡的訓練，訓練樣本的信噪比在-2～10 dB 之間等概率取值；測試樣本在信噪比為-2～10 dB的范圍內間隔2 dB取值，每類信號在每個信噪比下產生100個樣本。除Costas信號外，其他信號載頻均為10 MHz，采樣頻率均為70 MHz。噪聲類型為高斯白噪聲，具體參數設置如表1所示。

表1 信號主要參數范圍

4.1 仿真實驗1

一般來說，模型過于復雜或者輸入參數過多會導致模型出現過擬合的現象，圖6是本文提出的集成卷積網絡訓練集與驗證集損失與準確度曲線。從圖6中可以看出，本文提出的集成卷積神經網絡沒有出現過擬合的現象，在訓練過程中集成卷積網絡在50個迭代周期后開始收斂，訓練集和驗證集準確率均達到了98%以上，在收斂后驗證集損失和準確率曲線較為平滑，波動幅度比較小。網絡訓練效果比較好，網絡識別精度高。

圖6 集成卷積網絡訓練集及驗證集損失和準確度曲線

4.2 仿真實驗2

為了檢驗網絡對5類信號的分類能力，利用實驗1的神經網絡，同時設置一個單獨的卷積神經網絡，網絡輸入相同，在信噪比為-2～10 dB之間，每隔2 dB測試2種分類網絡對5類雷達信號的分類的正確率。圖7是2類網絡的分類情況。從圖7中可以看出，相較于單個卷積神經網絡，集成卷積神經網絡有更高的分類正確率，尤其是對容易混淆的Frank和P4碼信號來說，信號的準確率提高了10%左右，有效減少了易混淆信號識別精度不高的問題。這是由于集成網絡可以將不同網絡的結果進行結合，可以進行優勢互補，從而得到較好的識別結果。

圖7 單個網絡與集成網絡的識別正確率曲線

4.3 仿真實驗3

基學習器的數量對于分類器的性能也有很大的影響，為了研究基學習器數量對分類效果的影響，本文設置基學習器個數分別為2個、3個、4個和5個，同時設置一個CNN作為對照(記為1個基學習器)，分別比較他們的準確度和所用時間，結果如表2所示。

表2 基學習器數量性能的準確度和所用時間

從表2可以看出，相比于單個基學習器來說，增加基學習器的數量在不同程度上提升了模型識別的準確度，其中在4個基學習器的時候準確度最高，這說明通過增加基學習器的數量可以有效地提高網絡的性能。但是，當基學習器數量達到5個的時候，模型整體的識別準確率相對于上一個有所下降，這說明并不是基學習器數量越多越好，過多的基學習器不僅增加了學習訓練的時間成本，同時也增加了模型的方差，使得網絡抑制過擬合的能力下降，最終導致了模型精度的下降。實驗結果表明，基學習器數量在3～4個的效果相對較好。

5 結論

本文提出了基于Bagging和CNN的雷達信號分類方法，使用了信號的模糊函數特征作為網絡的輸入特征，利用卷積神經網絡作為基學習器進行訓練，然后將網絡的輸出特征進行集合得到最終分類結果。仿真實驗結果表明，相比于單個網絡訓練的方法，集成卷積神經網絡能夠更好地區分不同種類調制信號。對信號分類識別的實驗中，在-2 dB的信噪比下，也能達到85%以上的識別率，具有較好的分類識別能力。