一種基于路徑代價的TTE調(diào)度算法

劉國輝，祁志民

(北方自動控制技術(shù)研究所， 太原 030006)

基于調(diào)度時刻表(scheduling time-table)的通信調(diào)度是時間觸發(fā)以太網(wǎng)嚴格時間確定性和高完整性保障機制的關(guān)鍵。近年來，對TTE網(wǎng)絡(luò)的研究主要集中在TT調(diào)度表的離線設(shè)計。文獻[1-2]研究了RC流量對TT流量調(diào)度的影響，忽略了TT流量間的依賴性；文獻[3]通過改變TT消息在源端的觸發(fā)時間及中間傳輸?shù)穆窂剑芯苛薚T消息調(diào)度的時延變化，缺少了TT流量總體時間占比對結(jié)果影響的分析；文獻[4]設(shè)計了一種冗余至節(jié)點的雙以太網(wǎng)結(jié)構(gòu)，對于不同優(yōu)先級的消息采用不同的傳輸通道，研究了此狀態(tài)下TT流量調(diào)度的時延問題，缺乏對同一通道上不同消息影響機制的分析；文獻[5]在不限制TT消息的周期屬性的基礎(chǔ)上，對不同長度的TT消息匹配相應(yīng)的時間槽，研究了TT流量的調(diào)度問題，缺少對TT流量在已知端到端間不同路徑傳輸對TT流量調(diào)度影響的分析；文獻[6]在TTE的基礎(chǔ)上增加了流量隔離功能，研究了大規(guī)模實時任務(wù)下調(diào)度表的生成問題，但增加的通信規(guī)則使得TT流量分布趨于固定；文獻[7-8]提出將TT消息間的依賴度轉(zhuǎn)化為矩陣表示，研究實時任務(wù)的可調(diào)度性，但未考慮TT流量在整網(wǎng)分布的均勻度對TT流量調(diào)度的影響。上述研究都未綜合考慮TT流量時間占比及TT流量在端到端間不同路由的傳輸，對TT流量調(diào)度時延的影響。本文在已有研究的基礎(chǔ)上，提出了時間觸發(fā)以太網(wǎng)中實時任務(wù)調(diào)度算法，研究實時任務(wù)的時間占比及任務(wù)分配均衡度對整網(wǎng)延時的影響。

1 時間觸發(fā)以太網(wǎng)建模

TTE網(wǎng)絡(luò)拓撲定義[9-10]為賦權(quán)連通有向圖G=(V，E)，如圖1所示，其中V為網(wǎng)絡(luò)節(jié)點集合，在TTE網(wǎng)絡(luò)中為處理器和交換機的集合，V=(v1，v2，…，vN)，N為節(jié)點數(shù)量。E為連接節(jié)點的有向鏈路的集合，節(jié)點vi到節(jié)點vj(vi∈V，vj∈V)的有向鏈路l(l∈E)可以表示為l=vivj=lij；TTE網(wǎng)絡(luò)中采用全雙工鏈路，若有l(wèi)ij∈E，則lji∈E。

圖1 網(wǎng)絡(luò)拓撲的定義示意圖

定義：鄰接矩陣A=(aij)N×N，aij為

定義：兩確定節(jié)點vi，vj間任一路由g對應(yīng)的路由路徑(Pathij)g=〈lip，…，lpk，lkj〉；路徑矩陣R=(uij)N×N，uij取值0或1，代表節(jié)點vi與節(jié)點vj之間是否存在相鄰連接關(guān)系；鏈路帶寬矩陣C=(cij)N×N，cij是有向鏈路lij的帶寬；鏈路利用率矩陣H=(hij)N×N，是對應(yīng)于矩陣R中所有相連鏈路lij的鏈路利用率；路徑代價矩陣W=(wij)N×N，wij是節(jié)點vi有到節(jié)點vj的路徑的代價值。

定義：兩確定節(jié)點vi，vj間任一路由g所經(jīng)過鏈路的最大鏈路利用率為：

max(hPathijg)=max(hip,…,hpk,hkj)

定義：pathNum為路由數(shù)目，以max(h(Pathij)g)=max(h(Pathij)1，h(Pathij)2，…，h(Pathij)g)，表示節(jié)點vi到節(jié)點vj所選路由的鏈路利用率的最大值。

定義：任一路由的跳數(shù)為

定義：S=(sij)N×N，sij=hop(P)，表示節(jié)點vi到節(jié)點vj所選路由的跳數(shù)。

2 調(diào)度表結(jié)構(gòu)

TTE時刻表調(diào)度適用于具有多個空分網(wǎng)段的交換式網(wǎng)絡(luò)，每個進行TT通信的發(fā)送端，都存放有一個對應(yīng)的TT幀調(diào)度時刻表。

對于周期性TT通信任務(wù)，調(diào)度表整體定義為一個矩陣周期(Matrix Cycle，MC)，它由若干個基本周期(Basic Cycle，BC)組成[11]。

其中BC的值為所有TT消息傳輸周期的最大公約數(shù)，MC的值為所有TT消息傳輸周期的最小公倍數(shù)，矩陣周期表的行數(shù)為r=MC/BC。

如圖2所示，將每個基本周期人為劃分成兩段，即TT幀段、ET幀段。其中為實現(xiàn)TT消息的緊湊傳輸，定義時間窗Q，默認TT消息只在這個范圍調(diào)度。

圖2 周期結(jié)構(gòu)框圖

3 調(diào)度表生成

根據(jù)調(diào)度表整體定義，需要構(gòu)造一個矩陣周期表M=(mij)r×n，n為所有TT通信消息個數(shù)，又

其次，對于第i基本周期，即矩陣周期表第i行，需要構(gòu)造一個對應(yīng)的“通信任務(wù)—通信路由鏈路”通信狀態(tài)表TB=(ωuv)n×k，其中k為整網(wǎng)通信鏈路的個數(shù)，其中：

3.1 TT流量路由規(guī)劃

端到端路由的確定，需要考慮節(jié)點間通信的自由度，兩個具備通信關(guān)系的節(jié)點間可供選擇的路徑可能有多條。這里采用兩個參量限制通信的自由度，即負載均衡度和路由轉(zhuǎn)跳次數(shù)，綜合考量這兩個因素的相互約束，以期路徑較好的匹配。

3.1.1 路由評價函數(shù)

以Cost(P)=min(Max(hP))表示路由負載代價函數(shù)，Max(hP)是指所經(jīng)過鏈路的鏈路利用率的最大值，以此為指標(biāo)尋找目的路由，可繞開負載較大的鏈路，避免局部堵塞。Cost(P)=min(hop(P))為路由跳數(shù)代價函數(shù)，hop(P)是路由的跳數(shù)，以此為指標(biāo)尋找目的路由，可找到最小跳數(shù)的路由。

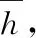
(1)

(2)

(3)

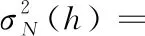
(4)

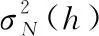
結(jié)合公式推導(dǎo)進行分析，兩種路由配置策略的根本區(qū)別在于通信任務(wù)流量的散布方式。綜合考慮兩個路由配置策略，提出兩者的加權(quán)代價函數(shù)——路徑代價函數(shù)，加權(quán)值為α和(1-α)，0≤α≤1，定義加權(quán)后的代價：

其中為了保證量級數(shù)的一致，采用標(biāo)準差。

3.1.2 加權(quán)值α的預(yù)選取

加權(quán)值α體現(xiàn)了整網(wǎng)的TT流量的負載均衡程度，與網(wǎng)絡(luò)的拓撲結(jié)構(gòu)、鏈路帶寬及消息經(jīng)過的路由等參數(shù)密切相關(guān)。

假設(shè)鏈路i的鏈路利用率為hi(0≤hi≤1)，對于整網(wǎng)的n條鏈路，其鏈路利用率分別為h1，h2，…，hi，hi+1，…，hn，并且h1+h2+…+hi+hi+1+…+hn=C(0≤C)。整網(wǎng)鏈路的負載均衡可以表述為h1，h2，…，hi，hi+1，…，hn之間的差值和最小化問題。根據(jù)切比學(xué)夫不等式取a∈CN，b∈CN，a={a1，a2，…，an}，b={b1，b2，…，bn}，且a1≥a2≥…≥an，b1≥b2…≥bn，得到：

令aj=bj=hi，可得加權(quán)值α，其計算公式如式(5)：

(5)

當(dāng)α=0時，min(Cost(P))相當(dāng)于最小跳路由代價函數(shù)；α=1時，min(Cost(P))相當(dāng)于負載均衡代價函數(shù)。

3.1.3 路徑規(guī)劃

步驟1：獲取TTE網(wǎng)絡(luò)參數(shù)，即建立A=(aij)N×N，C=(cij)N×N，S=(sij)N×N，初始化B=(bij)N×N，bij=0，H=(hij)N×N，hij=0，W=(wij)N×N，wij=0；

步驟2：預(yù)設(shè)的值，選擇對應(yīng)的路徑代價函數(shù)，將其嵌入到DFS路徑搜索算法中；

步驟3：設(shè)計尋找最小代價算法，流程如圖3所示，獲取兩確定節(jié)點間任務(wù)、路由匹配信息。

圖3 最小代價算法流程框圖

3.2 任務(wù)時間分配

3.2.1 TT消息影響系數(shù)

由于每條TT消息的發(fā)送、轉(zhuǎn)發(fā)和到達時間的確定都會對其余的TT消息的時間的確定造成影響，就需要確定那條TT消息對整個TTE網(wǎng)絡(luò)的影響最大，從而通過從影響最大的任務(wù)開始分配的方式，最大程度地減小TT消息間相互的影響。

在確定TT消息對整個TTE網(wǎng)絡(luò)的影響程度的過程中，主要依據(jù)以下四條原則[11]： TT消息的長度L越大，對TTE網(wǎng)絡(luò)的影響程度越大； TT消息的周期T越小，對TTE網(wǎng)絡(luò)的影響程度越大； TT消息的轉(zhuǎn)跳數(shù)N越大，對TTE網(wǎng)絡(luò)的影響程度越大； TT消息的所經(jīng)過的鏈路的負載越大，對TTE網(wǎng)絡(luò)的影響程度越大。

根據(jù)上述原則，定義了TT消息的影響系數(shù)U：

其中，dk為TT消息所經(jīng)過的鏈路lk的負載，即TT消息的影響系數(shù)U與TT消息所經(jīng)過的所有鏈路的負載之和成正比。

3.2.2 調(diào)度時刻表生成

圖4展示了調(diào)度時刻表的生成算法。結(jié)合該流程圖，可見具體的處理步驟如下：

步驟1：輸入TTE網(wǎng)絡(luò)的相關(guān)參數(shù)。包括鄰接矩陣、TT消息的長度、周期及消息路由路徑矩陣等；

步驟2：依據(jù)TT消息的長度、周期、傳輸路徑以及TTE網(wǎng)絡(luò)中各鏈路的負載，計算出TT消息的影響系數(shù)U；

步驟3：按照影響系數(shù)U的大小進行排序，決定TT消息的分配順序；

步驟4：根據(jù)TT消息的傳輸路徑生成“虛擬鏈路”，這里的“虛擬鏈路”與TTE網(wǎng)絡(luò)實時通信VL的概念完全相同。對應(yīng)矩陣周期表每一行，建立相應(yīng)的“通信任務(wù)—通信路由鏈路”通信狀態(tài)表TB，然后依據(jù)通信鏈路相關(guān)約束及TT消息時間窗Q的大小，建立整網(wǎng)鏈路通信時刻約束矩陣，運用MATLAB求解；

步驟5：若有可行解，則輸出時間表，結(jié)束算法；若沒有可行解，有兩種解決方法：一是直接結(jié)束算法；二是需要修改鏈路帶寬或個別消息特征值以達到可解目的。

圖4 調(diào)度時刻生成算法框圖

4 實例分析

TTE網(wǎng)絡(luò)包含4個終端節(jié)點，4個交換機，其網(wǎng)絡(luò)拓撲如圖5所示。

圖5 實例拓撲示意圖

網(wǎng)絡(luò)帶寬為1 000 Mbit/s，TT通信任務(wù)30個，得到一個矩陣周期內(nèi)特定時間段的調(diào)度時刻分布如圖6所示，在調(diào)度表可解的情況下，根據(jù)得到的調(diào)度時刻表，得出在一個矩陣周期中整網(wǎng)的鏈路利用率均值、鏈路利用率方差及整網(wǎng)通信最小時延與路徑代價函數(shù)中加權(quán)因子的關(guān)系圖如圖7～圖9所示。

圖6 調(diào)度時刻分布圖

圖7 鏈路利用率方差隨加權(quán)因子α的變化曲線

由圖7，圖8可知當(dāng)α=0時，即選擇最小跳數(shù)路由配置策略得到的鏈路利用率均值和方差最小，分別為0.218 7%，0.038；當(dāng)α=1時，即選擇負載均衡路由配置策略得到的鏈路利用率均值和方差最大，分別為1.538%，1.528。特別的，當(dāng)0.12≤α≤0.36時，鏈路利用率均值較大，而其方差較小，此時整網(wǎng)鏈路負載分配最佳。由圖9可知，整網(wǎng)最小時延在整體趨勢上隨α的階段增大而增加。由圖10可知，當(dāng)TT任務(wù)時間占比小于10%時，整網(wǎng)最小延時隨著占比增大呈線性增大。

圖8 鏈路利用率均值隨加權(quán)因子α的變化曲線

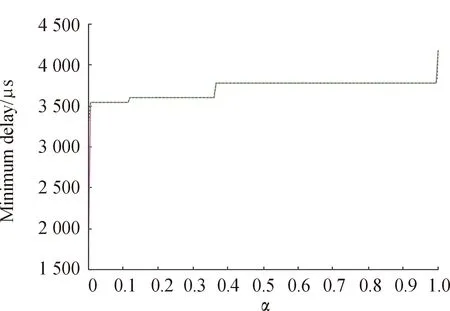
圖9 最小延時隨加權(quán)因子α的變化曲線

圖10 最小延時隨時間占比Q的變化曲線

5 結(jié)論

本文通過分析TT消息的調(diào)度特性，在路由分配過程中建立了評價函數(shù)，綜合權(quán)衡了負載均衡和路由跳數(shù)對調(diào)度表生成的影響。通過實際的案例仿真分析，得到了有效的TT消息靜態(tài)調(diào)度表，同時通過對比分析加權(quán)因子、TT消息時間占比與網(wǎng)絡(luò)最小延時的關(guān)系，為獲得最小延時的基礎(chǔ)上選取TT任務(wù)時間占比及任務(wù)在整網(wǎng)分布均勻度提供了一定的參考依據(jù)。