入水參數對彈塑性射彈入水影響的數值仿真

郭榮君，馮沐樺，李天雄，關 建，鐘垂琦，孫宇新

(南京理工大學 瞬態物理國家重點實驗室， 南京 210094)

運動體入水問題的研究至今已有較長的歷史，最初，學者Von Karman[1]引入了附加質量這個概念，獲得了求解入水沖擊載荷的理論方法。Herbert Wagner[2]考慮了楔形體入水過程形成的水面凸起及噴濺厚度，引入了楔底傾角修正因子，并采用伯努利方程，求解了楔形體沾濕表面的壓力分布。Shiffman和Spencer[3-5]進行了大量的球體和錐體垂直入水理論研究。

Romain等[6]引入FCB概念，使用 ABAQUS /Explicit 軟件對非對稱體垂直入水進行數值模擬研究。Bao等[7]開展了低速非對稱體楔形體垂直、傾斜和旋轉角度進入水數值仿真研究。Korobkin把入水過程流體運動分為五個階段[8-10]并建立了模型進行了具體的研究。

葉取源[11-12]建立了圓錐體垂直入水的三維數值模型，得到了入水空泡從形成、發展到閉合的變化規律。張岳青等[13]對于魚雷入水的忽撲現象進行了研究，針對魚雷入水復雜的過程， 利用實驗和數值仿真結合的方法，對造成忽撲的低壓力進行了分析。王瑞琦等[14]進行了平頭彈丸低速入水實驗與數值仿真，通過獲得不同時刻的實驗圖像和數值仿真圖像，對表面閉合空泡和深閉合空泡進行了分析，獲得了射彈沖擊水面時產生的射流對射彈運動的影響。熊天紅等[15]在實驗室的水靶道中進行了 4 種不同結構參數的射彈實驗，并使用 FLUENT 軟件針對實驗做了一系列數值仿真，對影響射彈阻力特性的彈體長徑比、空化器直徑、空化數等因素進行了分析。

以開展高速射彈入水轉向彈道特性研究為背景，本文擬運用數值仿真方法對不同角度、不同入水速度的射彈高速入水轉向問題進行研究，分析系列入水參數下，彈塑性射彈入水過程受力情況，揭示射彈入水轉向規律，具有一定的參考價值。

1 計算模型

1.1 有限元模型

本文采用AUTODYN 軟件進行數值仿真。

對于高速射彈入水問題，本文采用一種切削15°的射彈結構，如圖1所示。其網格使用Workbench軟件進行劃分，因為形狀比較復雜，采用六面體網格效果不好，因此采用的四面體自由網格劃分，彈身長78.5 mm，直徑 12.7 mm，網格尺寸大小選取1.5 mm，典型網格示意圖見圖2。

圖1 射彈示意圖

圖2 典型網格示意圖

為減小計算量采用二分之一模型進行計算。水域尺寸設置為射彈各尺寸的10倍，水域尺寸為800 mm、800 mm、60 mm，網格尺寸大小為1 mm，網格總數為38 400 000 個。射彈入水處設為距離右邊界四分之一處，選定標準之后的局部網格劃分如圖3。

圖3 計算模型局部網格圖

針對8種情況做了數值仿真計算，具體編號如表1所示。

表1 各種入水條件編號

1.2 材料模型和參數

射彈的材料模型選取STEEL S-7 高強度鋼材料，狀態方程則選取Shock狀態方程，強度模型則選取JC強度模型，該種材料模型的狀態方程參數如表2所示。

表2 STEEL S-7材料參數

在1983年，Johnson GR和Cook W.H提出了Johnson-Cook(JC)模型，該模型對溫度以及應變較敏感，且其參數通過實驗數據擬合相對比較容易獲得，能夠較好地描述金屬材料的應變和由于溫升出現的軟化效應，這種材料本構在沖擊、爆炸等領域均有通用性較強等優點。對于本文射彈高速入水轉向引起的大變形、高應變率等問題，采用該強度模型可以提供還原度較高的模擬，該模型屈服應力定義為：

其中

表3 STEEL S-7的Johnson-Cook強度模型參數

水的多項式狀態方程根據壓縮狀態的不同具有不同的形式。

當水壓縮時(μ>0 時)，狀態方程為:

P=A1μ+A2μ2+A3μ3+(B0+B1μ)ρ0e

當水膨脹時(μ<0時)，狀態方程為:

P=T1μ+T2μ2+B0ρ0e

當水既不壓縮也不膨脹時(μ=0時)，可以簡化為同一形式:

P=B0ρ0e

式中:P為水中壓力;μ為壓縮比，μ=ρ/ρ0-1;e為水的內能;ρ0為水密度。

水的SHOCK狀態方程為:

P=PH+Γρ(e-eH)

式中，PH和eH分別為材料沖擊Hugoniot態的壓力和比動能;Γρ為Gruneisen系數。

這里假設Γρ=Γ0ρ0=常數，且

式中:ρ0和e0分別為材料初始密度和聲速；μ為材料的壓縮比；λ為沖擊Hugoniot參數；λ和e0為常數，由以下沖擊波實驗關系式確定:

D=λu+e0

式中：D為沖擊波速度;u為波后質點速度。

2 射彈入水應力分析

為了便于進行分析，對彈體進行上、側、下部的定義，彈頭切削平面與彈體軸線為15°角(參見圖1)，在彈體入水運動過程中，彈頭的切削平面朝向水域，因而與彈體切削平面同一側的彈體部位定義為彈體下部，與之相反，在彈體切削平面另一側的彈體部位定義為彈體上部。選用工況3的射彈對其入水航行初期、航行中期及航行末期進行受力分析，所得壓力云圖如圖4～圖6所示。

圖4 0.5 ms時刻射彈上、側、下部壓力云圖

圖5 1.5 ms時刻射彈上、側、下部壓力云圖

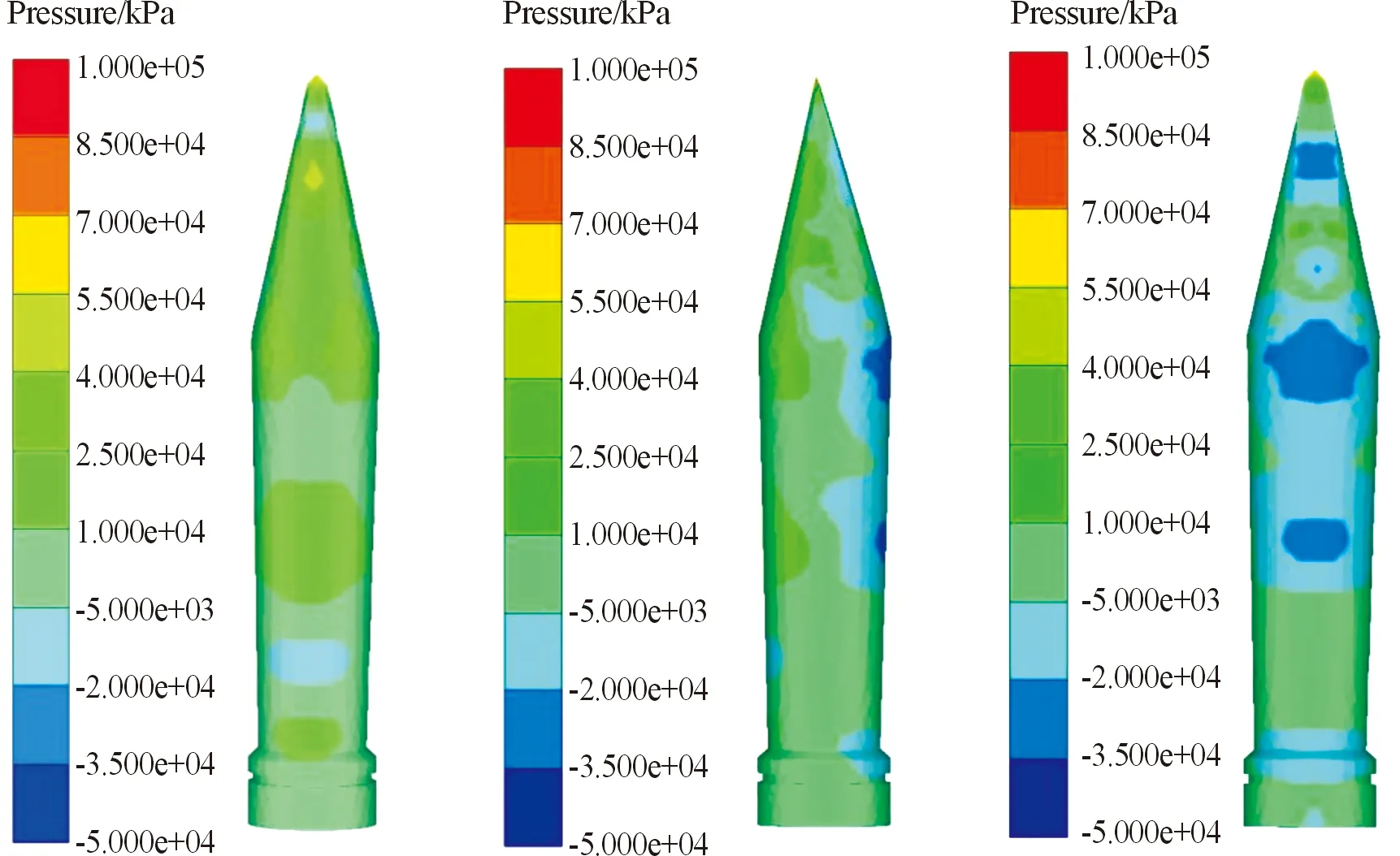
圖6 2.5 ms時刻射彈上、側、下部壓力云圖

由云圖可以看出，航行初期(0.5 ms)射彈壓力主要集中在頭部，而射彈中部至尾部受力非常小，此時由運動軌跡(圖7)可以看出，射彈剛入水時形成超空泡，射彈后部幾乎沒有碰到水域，頭部是主要的受力部分。在航行中期(1.5 ms)壓力則主要集中在射彈下部，此時射彈下部基本全部與水域接觸，而射彈上部進一步遠離水域，導致頭部受力略微增大。在航行后期(2.5 ms)，射彈上部受力持續減小，射彈下部壓力受力位置有向彈尾移動的趨勢，原因是隨著入水時間的推移，空泡有閉合的趨勢，這個時刻與 1.5 ms時刻相比彈尾與水域接觸的更徹底，且射彈偏轉角度更大，射彈前部受力更小，因此呈現出受力位置向彈尾移動的趨勢。同時射彈上部仍不接觸水域，主要受力與彈體前部的受力及彈頭的應力有關，因此射彈上部受力也更小。

圖7 各時刻射彈入水軌跡圖

3 入水角度影響分析

由于射彈垂直入水時，射彈會出現彈道失穩的情況。由此，本文采取斜入水的方式進行仿真，為了方便建模與分析，采用 60°和 75°兩種入水角度。通過仿真得出的數據繪制出相同入水速度下不同入水角度的俯仰角變化曲線，進行入水角度對射彈入水轉向影響的分析，仍規定俯角初始為正，仰角初始為負，如圖8。

圖8 各速度下俯仰角曲線

由圖8可以看出，俯仰角曲線中，前0.5 ms由于射彈只有頭部受力，彈身與水域不接觸，俯仰角變化與入水角度關系不大，兩種角度下的俯仰角減小的速率相當。

當0.5 ms之后射彈俯仰角在 0.5～1 ms之間由于發生了第一次忽撲，俯仰角快速減小，而60°的射彈俯仰角下降速率更大，說明在從忽撲中恢復之后，入水角度為60°的射彈轉向更大。1 ms之后，兩種入水角度的俯仰角下降速度都開始變緩，初始角度為60°的射彈在之后的階段角度變化速率稍快。說明入射角度為60°的射彈轉向效率較高。

規定水平方向速度為Vx豎直方向速度為Vy，其曲線如圖9、圖10所示。

水平方向速度上，入水角度為75°的射彈水平速度在波動的同時有明顯提升，而通過具體數據分析，速度提升至少 50%以上，而入水角度為60°的射彈水平速度提升不顯著，提升不超過 20%，從這一點上來看，入水角度 75°比入水角度60°對射彈轉向的影響更好一些。從速度曲線的波動程度來看，入水角度60°射彈的水平方向速度波動程度更小一些，而入水角度 75°的射彈水平方向速度波動程度更大一些，同時入水角度為60°的射彈忽撲開始都要略早于入水角度為75°的射彈，忽撲結束也早于入水角度為75°的射彈，且每個忽撲周期入水角度為 60°的射彈都比入水角度為75°的射彈短，其在2.5 ms之前共發生4次忽撲，而入水角度為75°的射彈在 2.5 ms之前共發生3次忽撲，說明射彈在發生忽撲之后，入水角度為60°的射彈比入水角度為75°的射彈可以更快地恢復彈道穩定，主要是由于在相同時間下，入水角度為60°的射彈彈身下部接觸水域面積比入水角度為75°的射彈大，受力更均勻，因此彈道更容易恢復穩定，于是在相同時間內忽撲的次數更多，且在不斷地忽撲過程中，射彈逐漸轉向。綜上所述，入水角60°對射彈轉向更為穩定更有利。

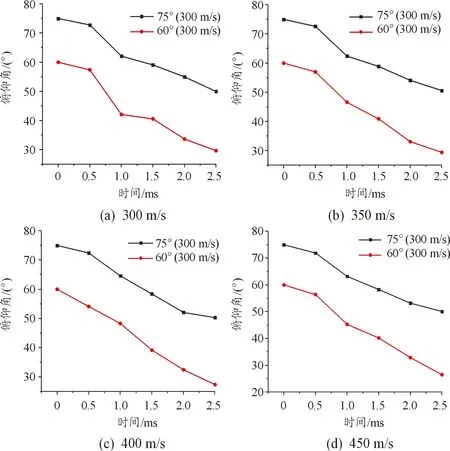
圖9 各初速下不同入射角度水平方向速度曲線

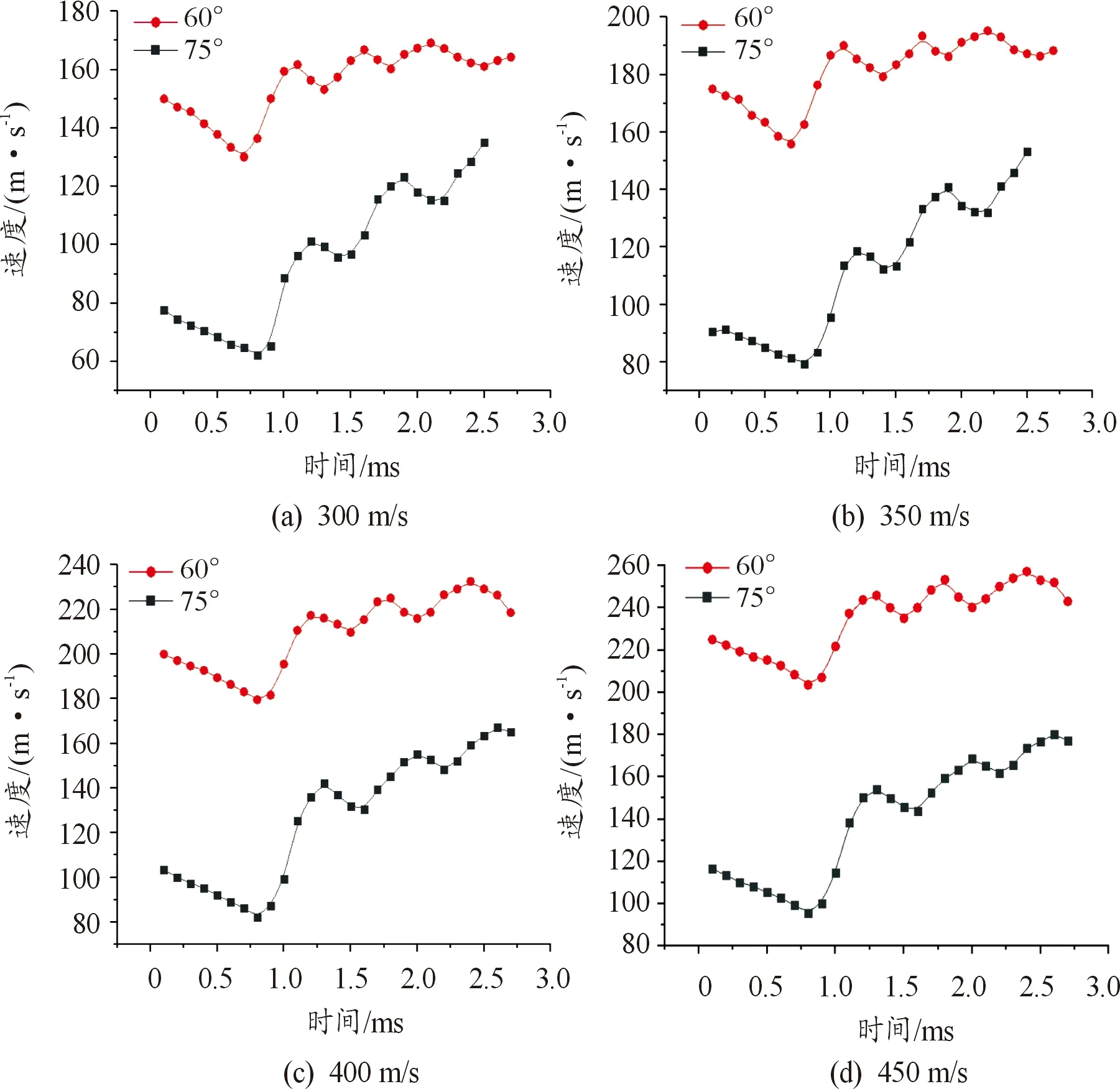
圖10 各初速下不同入射角度豎直方向速度曲線

4 入水速度影響分析

由于在各種速度條件下環境存在差距，可能會對射彈入水產生影響，因此繪制出相同入水角度下不同入水速度的俯仰角變化曲線，進行入水速度對射彈入水轉向影響的分析，仍規定俯角初始為正，仰角初始為負，如圖11所示。

圖11 入射角度為60°、75°下俯仰角曲線

由俯仰角曲線圖中可以看出，0.5 ms之前，射彈剛入水，4種速度下俯仰角變化幅度都很小，但可以明顯看出入水速度較低的射彈俯仰角變化更為劇烈，根據數據分析，0.5 ms時刻入水速度為400 m/s的射彈俯仰角要比其他速度的射彈要低3°～4°，可以看出在0.5～1 ms之間，射彈俯仰角變化較大，上文中也進行了分析，由于正好處于第一次波動最大的忽撲狀態，因此俯仰角變化較大，1 ms之后，射彈俯仰角變化趨于平緩，這時速度最小的射彈，俯仰角變化最為平緩，在這之后四種速度的彈體俯仰角變化趨于一致，速度較小的彈體變化相比于速度較高的彈體變化略為平緩，差別很小可以忽略不計。從穩定性和轉向效率來說，在后期穩定性相差不大的情況下，轉向效率更好的入水速度明顯對射彈入水轉向有著更好的影響，在本文的速度范圍內，入水速度更高的射彈有著更好的穩定性和轉向效率。

由速度曲線可以討論期間發生的各種變化，例如各種射彈經歷的忽撲，以及在亞音速和超音速條件下對射彈的各種影響，也是討論入水速度對射彈的轉向能力影響的重要因素。規定水平方向速度為Vx豎直方向速度為Vy，以及合速度Va，有關曲線如圖12～圖14。

由圖可知，初入水時，由于只有頭部受到阻力，因此彈體水平方向速度下降率差距不大，而速度更低的彈體到達忽撲點的時間更早，而速度更高的彈體忽撲時間點隨速度的增大而略微滯后，到達忽撲點后，水平與豎直方向上的速度變化都十分劇烈，在之后時間里，射彈在經歷了第一次忽撲之后速度都隨著之后的忽撲呈現波動上升的狀態，可以看出，在第1次上升與第2次上升時，入水速度更高的射彈速度上升幅度要大于入水速度低的射彈，其后上升幅度逐漸接近，說明入水速度更高的射彈在將速度轉換為水平方向速度上更有優勢。

豎直方向速度上，初入水時速度下降仍然不快，射彈豎直方向速度隨著每一次的忽撲呈波動下降狀態，入水速度高的射彈豎直方向速度下降地要比入水速度為低的射彈快，且入水速度高的的射彈豎直方向速度逐漸靠近入水速度低的射彈，原因之一是射彈速度快則彈體受力更大，減速更快，其二是從之前的分析中可以得出，由于射彈進行了更大的轉向，因此豎直方向速度有一部分轉換為水平方向速度。總的來看入水速度越高的射彈，轉向能力與穩定性更好，同時能量損失相比于低速射彈并沒有太大。

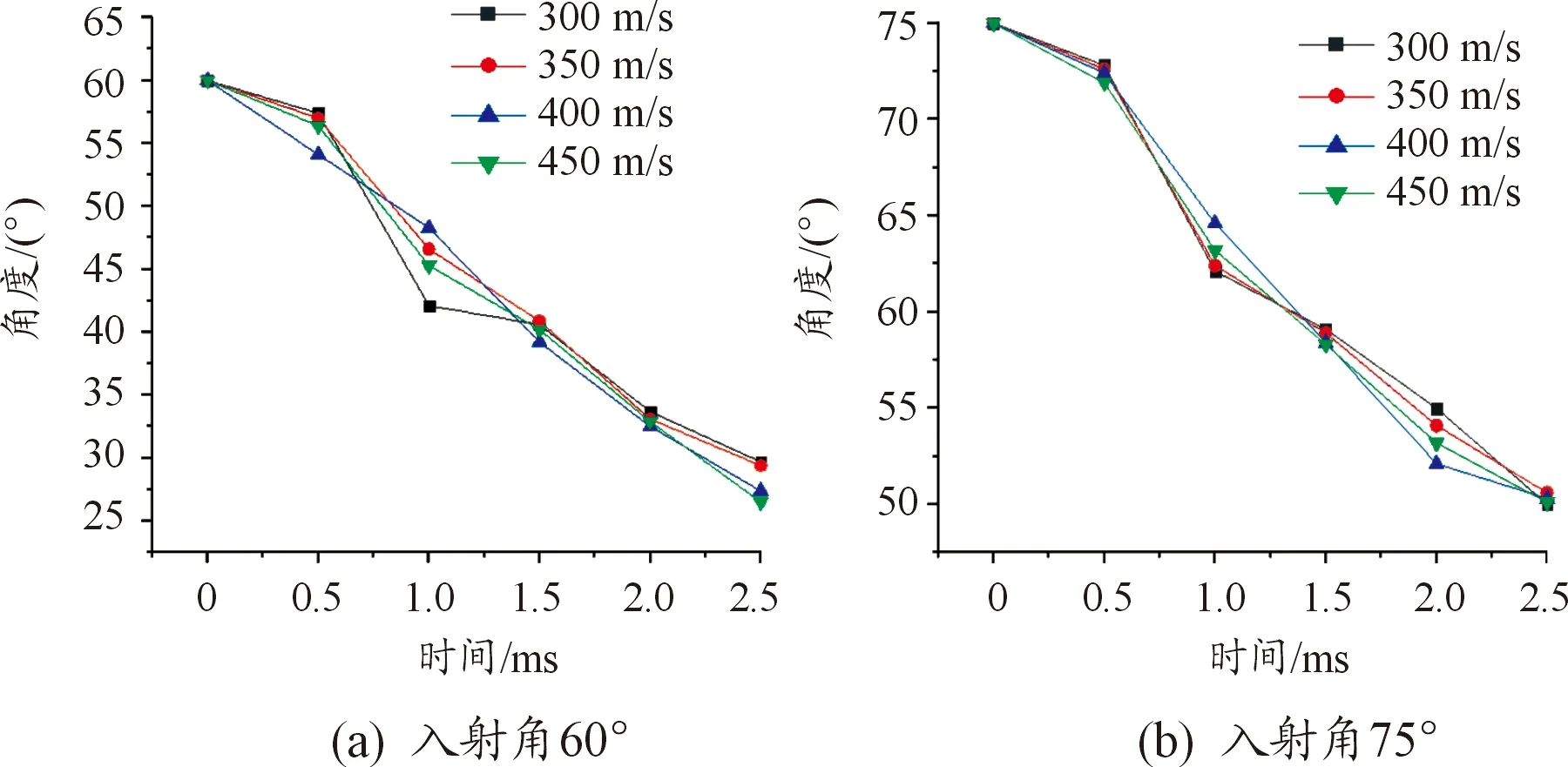
圖12 入射角為60°與75°條件下各初速水平方向速度曲線

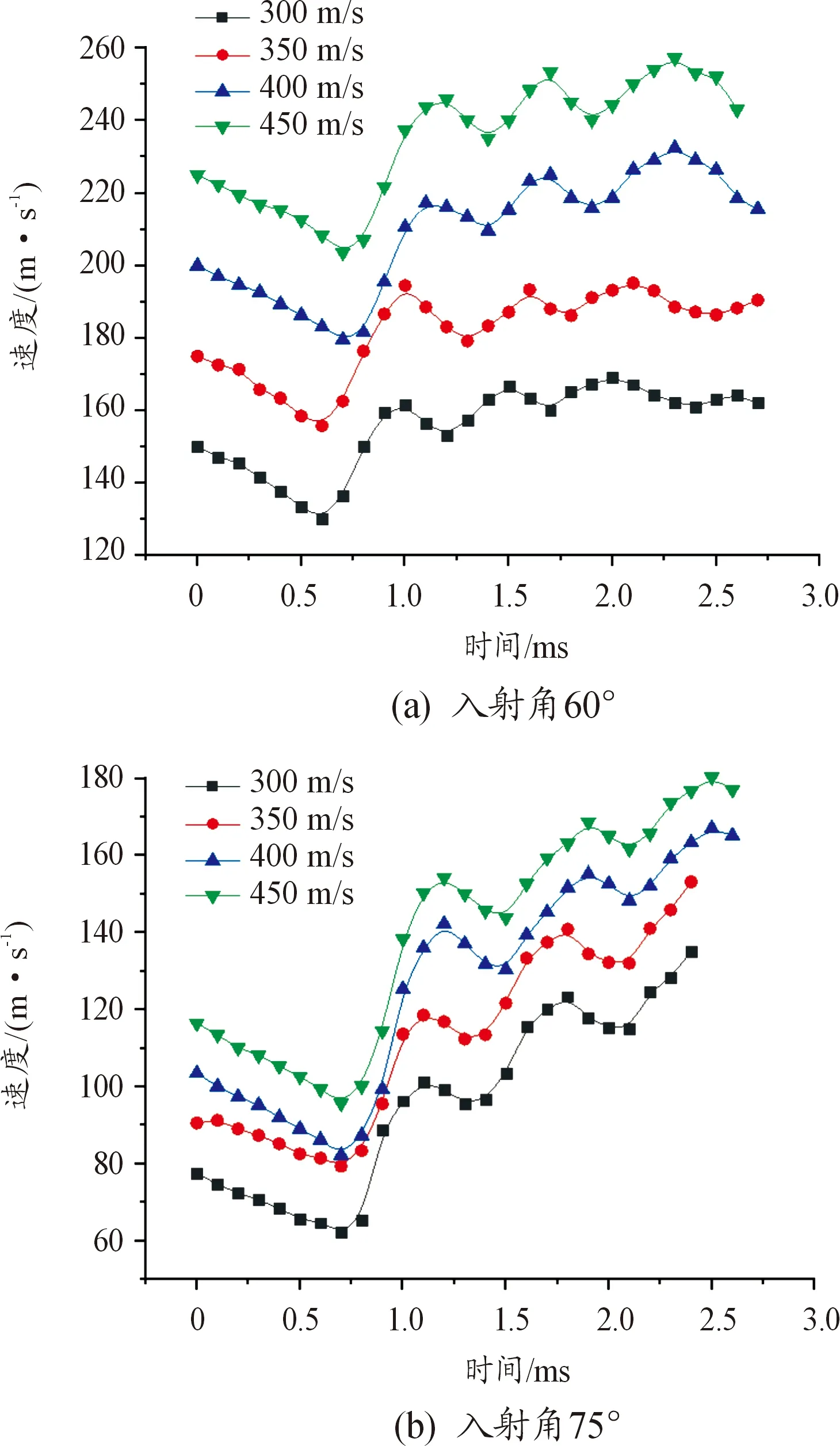
圖13 入射角為60°與75°條件下各初速豎直方向速度曲線

圖14 入射角為60°與75°條件下各初速射彈合速度曲線

5 結論

1) 彈塑性鋼制射彈入水初期應力應變主要集中在射彈的頭部，應力在入水初期增加極快，隨著入水時間的增加，射彈下部受力變大，而射彈上部逐漸遠離水域，射彈逐漸完成轉向。

2) 帶有15°切削角的異形彈塑性射彈在入射角度分別為60°和75°的跨介質入水過程中都展現了良好的轉向性能，其中入射角為60°的射彈的穩定性及轉向性能更為優良。

3) 在相同入射角的情況下，在300 m/s到450 m/s的速度范圍，隨著射彈速度的提高射彈入水后的彈道穩定性提升，且轉向性能提高，但能量損失增大，在入水速度為450 m/s情況下0～2.5 ms間彈體的動能損失是入水速度為300 m/s情況下動能損失的2倍以上。速度更高的射彈具有更好的轉向性能與穩定性，但彈體能量損失也更大。