基于需求側管理的電力用戶能耗預測分析?

樊立攀 李勁松 霍偉強 田曉霞 傅 晨

（國網湖北省電力有限公司 武漢 430000）

1 引言

在供電需求側管理中，根據用電情況、天氣預報和建筑物內供熱、供冷系統的特點進行用電需求分析和預測，有助于電力部門掌握居民用電的動態行為，為電力需求側管理提供決策依據，對優化供電側調度管理和提高低壓供電質量都具有參考意義［1～3］。建筑能耗預測方法主要是利用線性回歸算法［4］、決策樹算法［5］、神經網絡算法［6］和支持向量機［7］來概括輸入特征與輸出預測之間的映射關系。目前大多數關于住宅建筑的研究都立足于對建筑能耗的短期能耗預測（每小時）或長期預測（每年），以削減一天內高峰時段用電量或確定電網規劃和投資的要求，但是面向區域需求側管理的大量住宅建筑的月用電量預測研究相對較少［8～9］。為此，本文提出一種能夠準確預測住宅用電量的模型。試驗表明，該模型能夠通過精確的分類結果較準確地預測該地區未來一個月的電力需求側狀況和分布，為供電的調度和控制提供可靠的數據支撐。

2 預測方法

2.1 方法概述

本文所提出的針對住宅建筑能耗預測問題的解決方案如圖1所示。首先，對從數據庫中獲取的數據進行預處理，包括住宅建筑的特征、天氣信息和能源消耗，以去除數據中的噪聲、異常值和缺失值。在預處理之后，對數據集進行特征提取。提取方法是首先進行數據特征描述和數據歸一化處理，隨后通過特征工程從數據中提取有效信息，最后進行特征維數約簡。在預測住宅用戶用電量前，首先利用PSO-K-means算法對每個季度的用電量數據進行聚類分析，然后根據聚類中心點將每個季度的用電量值劃分為相應的水平。經過數據采樣后，采用SVM模型對輸入的是住宅建筑的特征、天氣信息和歷史能耗數據（即上月的天然氣和電力消耗）進行計算，輸出為下個月的住宅用戶用電量水平。下面對四個關鍵算法進行闡述。

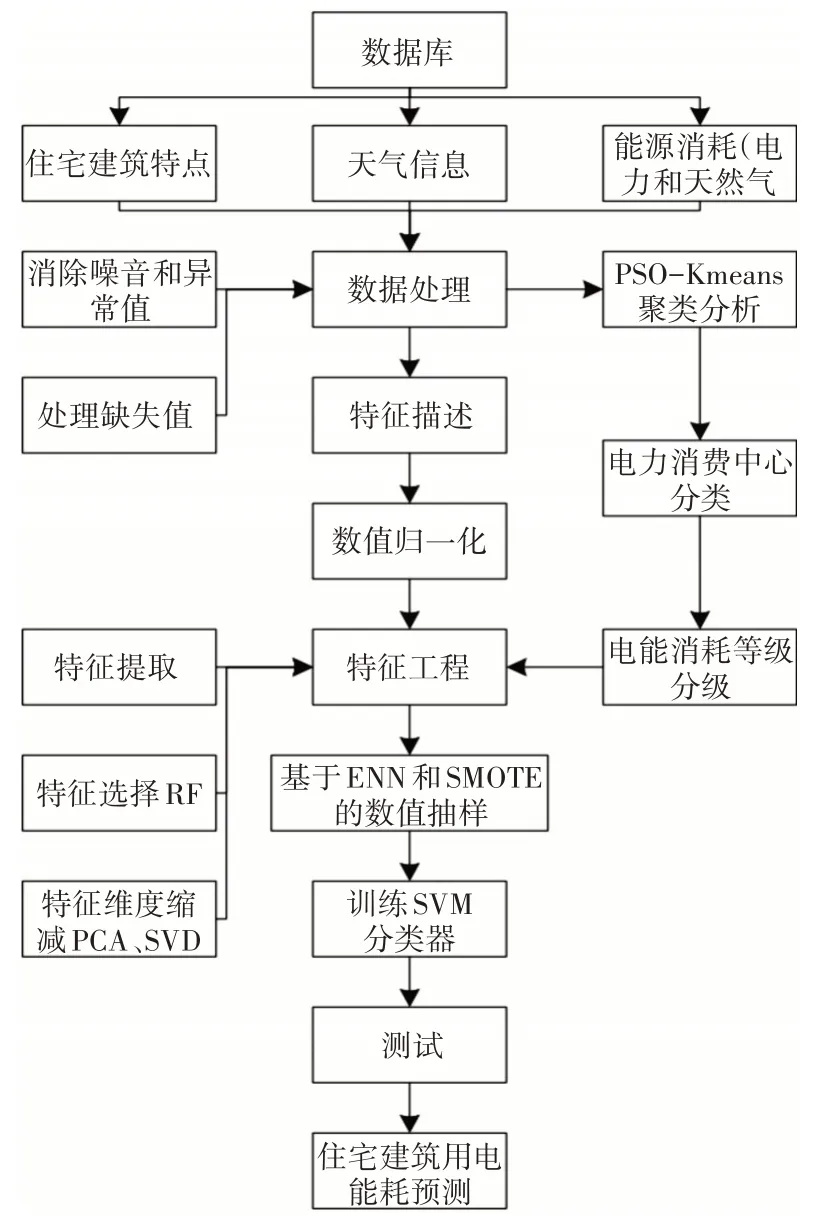
圖1 住宅建筑用電能耗預測

2.2 PSO-K-Means聚類分析

在預測住宅建筑的電能消耗等級之前，利用K-means聚類算法分析了數據的分布規律。本研究將電能消耗數據分為四個季度，然后提取每個季度三個月的值作為特征向量。例如，第一季度的特征向量為1月份的電能消耗，2月份的電能消耗，3月份的電能消耗。

K-means聚類算法具有收斂速度快、穩定性好等特點。然而，聚類過程無法確定聚類中心的數量。本文引入適應度sdbw值作為聚類結果的評價指標。sdbw不僅考慮了聚類內的緊湊性，還考慮了兩個聚類之間的密度問題。適應度值越小，聚類效果越好，說明聚類內連接越緊密，聚類間分離越大。

設D=｛Vi｜i=1，2…，c｝將數據集S劃分為c個凸聚類，其中vi為每個聚類的中心。從中心到聚類Stdev點的平均距離計算公式如下［13］：

有效性指數sdbw定義為

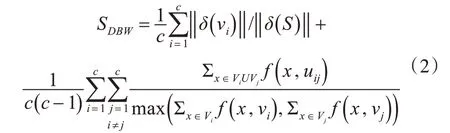
式（1）和式（2）中δ（vi）是聚類vi的方差，δ（S）是數據集的方差，vi和vj分別是聚類vi和vj的中心，uij是由vi和vj的中心定義的線段中點。如果中心u與點x之間的距離d（x，u）大于聚類Stdev的平均標準差，則f（x，u）=0；否則，f（x，u）=1。

聚類效果取決于初始聚類中心的選擇。為了解決這一問題，本文采用改進的粒子群優化算法（PSO）作為K-means聚類算法的前一步。

假設n維空間中有m個粒子運動。在這一點上，在所有粒子中都找到了每個粒子各自的最佳位置pbestk和全局最佳粒子位置gbest。對于任意粒子k，位置xk和飛行速度vk根據以下計算公式進行調整：

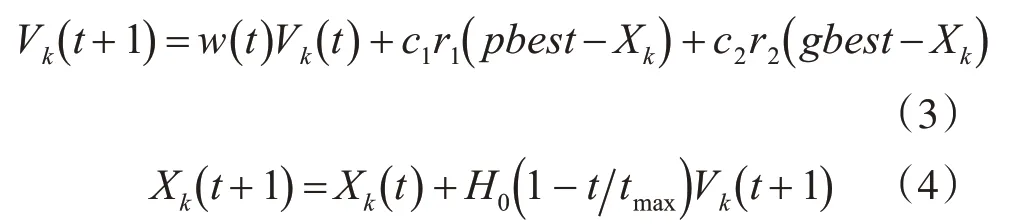
采用線性調整策略動態調整公式中的權重：

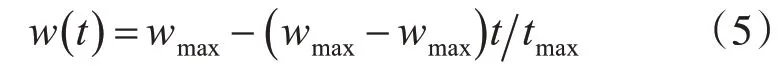
上式中w（t）是慣性權重函數，c1是認知權重因子，c2是社會權重因子，r1和r2是在［0，1］范圍內均勻分布的兩個隨機數，wmax和wmin分別是初始和最終慣性權重因子，tmax是最大迭代數，t是當前迭代數。

在迭代的后期，優化算法的搜索速度趨于緩慢，適應值趨于穩定。因此，本研究引入適應度方差的閾值以完成迭代，其計算公式如下［14］：

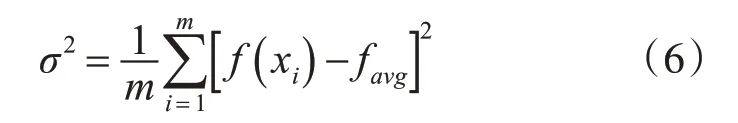
式（6）中m為群中粒子數，f（xi）為單個粒子的適應度值，favg為粒子群的平均適應度。

PSO-K-means算法的實現如算法1所示。

算法1 PSO-K-means算法

輸入：聚類數據集（居民用電量）S=｛x1，x2，…，xw｝，聚類中心數c，粒子群大小m，最大迭代數t max

輸出：聚類分類D=｛V1，V2，…，Vc｝

1）迭代s次，找到每個維度的最大值和最小值作為位置范圍［xmin，xmax］，其中速度范圍為［-xmax，xmax］；

從S中隨機選擇c個初始化中心，然后重復并生成m粒子群；

使用式（2）計算每個粒子的適應度值sdbw；

初始化pbestk和gbest；

2）for（迭代次數＜tmax）do

for（k=0，1，…，m）do

根據式（3）和（4）更新粒子的速度和位置，并確保速度和位置在控制范圍內；

根據式（5）動態調整權重；

end for

for（數據點=1，2，……，w）do

使用歐幾里得距離將每個數據點劃分進最近的簇；

使用式（2）計算適應度值sdbw；

if sdbw＜個體極值，則更新pbestk和gbest；

end for

使用式（6）計算粒子群的適應度方差；如果適應度方差＞閾值，轉至步驟3）；

end for

3）獲取最佳數量的群集中心C和gbest；

執行k-means算法；

4）從粒子群優化算法的結果中選擇最小sdbw的PC粒子作為初始聚類中心；

5）for（數據點=1，2，……，w）do

使用歐幾里得距離將每個數據點劃分進最近的聚類；

end for

for（聚類數量=1，2，……，c）do

更新每個聚類的平均值并標記中心點；

end for

如果聚類中心點沒有更改，則返回聚類分類D=｛V1，V2，…，Vc｝。

2.3 抽樣算法

為了解決數據分類不平衡的問題，本研究采用最近鄰（ENN）算法［15］和合成少數技術（SMOTE）算法［16］分別對大多數類別數據和少數類別數據進行抽樣，以實現對數據集的平衡，為下一步的數據分類處理提供方便。

算法2 ENN算法

輸入：原始數據集T，相鄰樣本個數K

輸出：過采樣后的數據集TENN

1）i=0，TENN=T；

2）while（i＜抽樣個數）do

比較數據集T中xi周圍的K個相鄰樣本的類別和xi的類別，如果不同，則刪除xi；

end while

SMOTE通過在少數類數據點之間隨機插入新的樣本來平衡樣本。該方法在一定程度上避免了分類器的過度擬合，提高了分類能力和預測精度。

在本研究中，抽樣算法集成了ENN與SMOTE以平衡數據集，將數據集分為不同的電能消耗等級。大多數類別中的數據被抽樣采集（刪除了一些數據點），少數類別中的數據被對偶取樣（添加了新的數據點），以改進后續SVM分類器的預測結果。SMOTE算法如算法3所示。

算法3 SMOTE算法

輸入：數據集TENN，相鄰樣本數k，過采樣率n

輸出：數據集TSMOTE

1）i=0；

2）while（i＜抽樣個數）do

在xi附近找到K個相鄰的樣本，選擇n個樣本xij

for j=1，2，…，n

根據以下計算公式對新的少數類別樣本yj進行擬合：yj=xi+（xi-xij）rand（0，1）；

end while

3）將yj加入數據集TSMOTE

2.4 SVM方法

SVM是一種被廣泛使用的機器學習分類算法［17］。由于SVM方法具有訓練過程簡單，輸入量少的優勢，本研究使用該分類對用電量數據進行分類處理。

當數據線性可分時，SVM解決分類問題的方法為

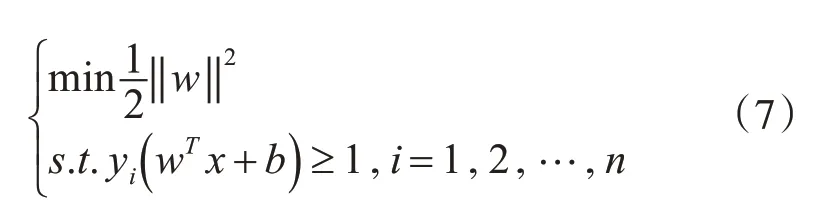
在SVM理論中，通常將拉格朗日乘子引入目標函數，使得目標函數呈現對偶形式易于求解。拉格朗日函數的形式如下：

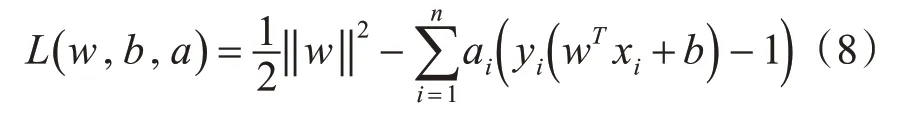
其中w和b是通過計算a得到的，w是歐幾里得范數，ai（i=1，2，…，n）是拉格朗日乘數。對偶問題定義如下：

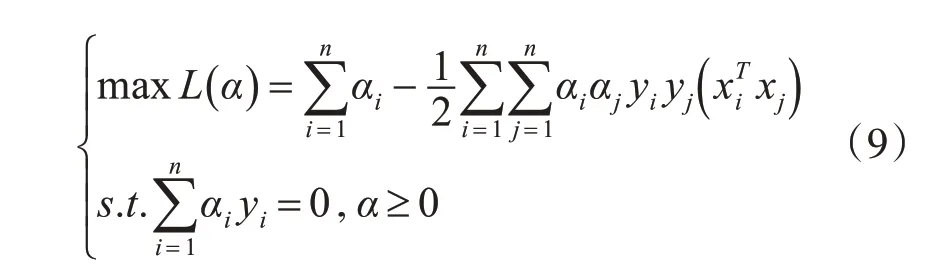
隨后將對偶問題轉化為目標函數的極值問題：

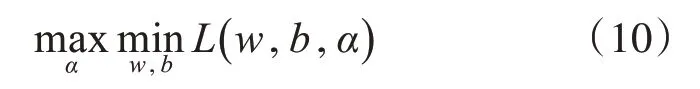
分類超平面的計算方法為

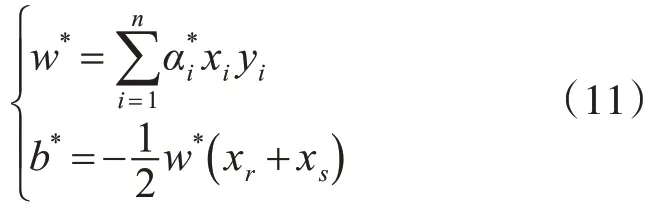
其中，是最佳拉格朗日乘數，xr和xs是兩類支持向量中的任意一對。

本研究的用電量水平的預測是一個多分類問題，因此需要將其分為多個二分類問題。劃分策略采用OvR（一對剩余）的形式。可以使用OvR為每個類訓練一個分類器，其中特定的類被認為是正類，所有其他的樣本被認為是負類。在實驗中將使用n個分類器將具有最高置信度的類標簽分配給特定的樣本。

3 實驗

3.1 實驗設置和評價指標

本文利用湖北省武漢市電力公司和武燃集團提供的2018年度公共能源消耗數據，對上述能耗預測方法進行了測試。所使用的公共能源消耗數據包括住宅建筑的特點和每月的電力和天然氣能耗。測試算法采用python實現。試驗平臺為一個Windows10操作系統，該操作系統采用Intel酷睿i7 2.7GHz處理器和16GB RAM，軟件平臺為pycharm和anaconda。采用三個常用的評價指標：準確度、精密度和召回率對預測性能進行量化衡量。

3.2 住宅建筑的用電量分類

實驗得出的每個季度不同深度顏色的聚類結果如圖2所示。根據最優適應度值計算聚類中心，如表1所示，劃分各住宅建筑月用電量類別。例如，第一季度單位面積用電量低于0.287 kWh/m2的住宅建筑劃分為1級。

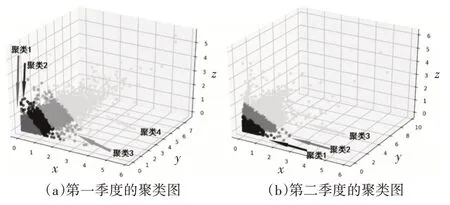
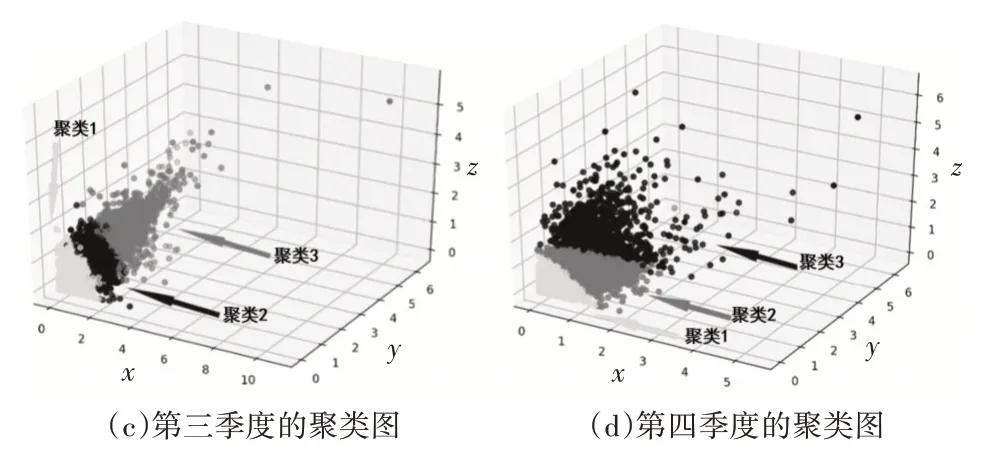
圖2 每個季度的聚類結果（x、y、z坐標表示每個季度三個月單位面積的電能消耗（kWh/m2））

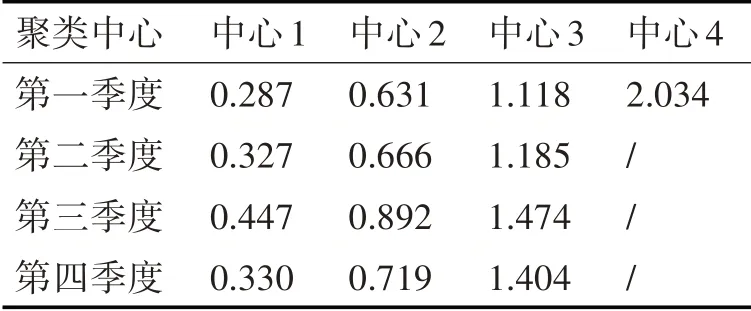
表1 各季度單位面積耗電聚類中心

然后統計每個季度不同等級的住宅建筑數量，如表2所示。第一季度的用電量從高到低可以分為五類，而其他三個季度可以分為四類。

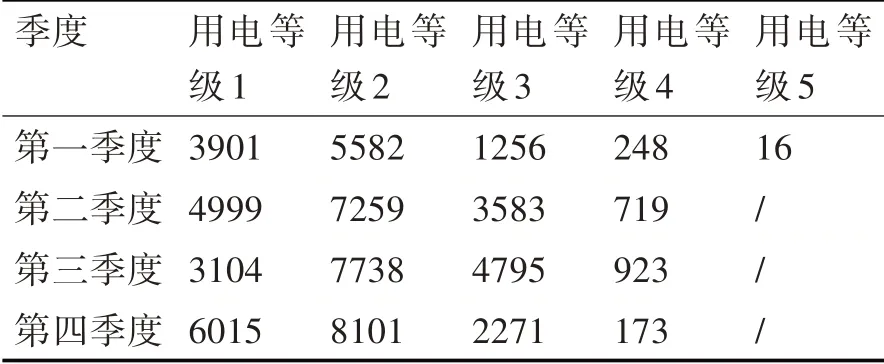
表2 每個季度的聚類統計數

3.3 數據抽樣和過度采樣

利用聚類算法解決了住宅建筑電能消耗的分類問題，但根據上述內容，出現了一類不平衡問題。本文采用數據抽樣和過度采樣相結合的方法來解決電力能耗數據的不平衡問題，并采用SMOE-ENN算法對不平衡數據集進行處理。圖3顯示了原始的一個季度與四個季度中的一個季度之間的比較圖。抽樣處理后的數據包含14個結構變量，14日天氣變量和兩種歷史能源消耗變量（前一個月的天然氣用量和用電量），為了方便對比顯示原始數據和，通過PCA算法將抽樣處理后的數據維度減少到三個維度（坐標軸沒有物理意義）。

3.4 試驗結果

試驗數據來自于武漢市電力公司和武燃集團公開的2018年度公共能源消耗數據。其中第二、三、四季度用于電力預測的住宅共16560棟，但一季度用于試驗的住宅11003棟的能耗數值缺失。為了預測每月的電能消耗等級，80%的處理數據集用于訓練，20%用于測試。對GBDT、BP和SVM每種模型重復實驗20次。表3中的實驗結果說明了本文所述的模型在預測住宅建筑用電上的具有最優的性能指標。

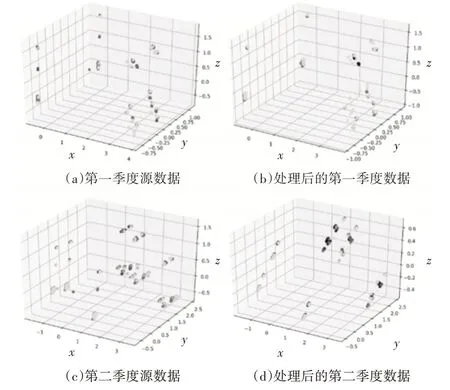
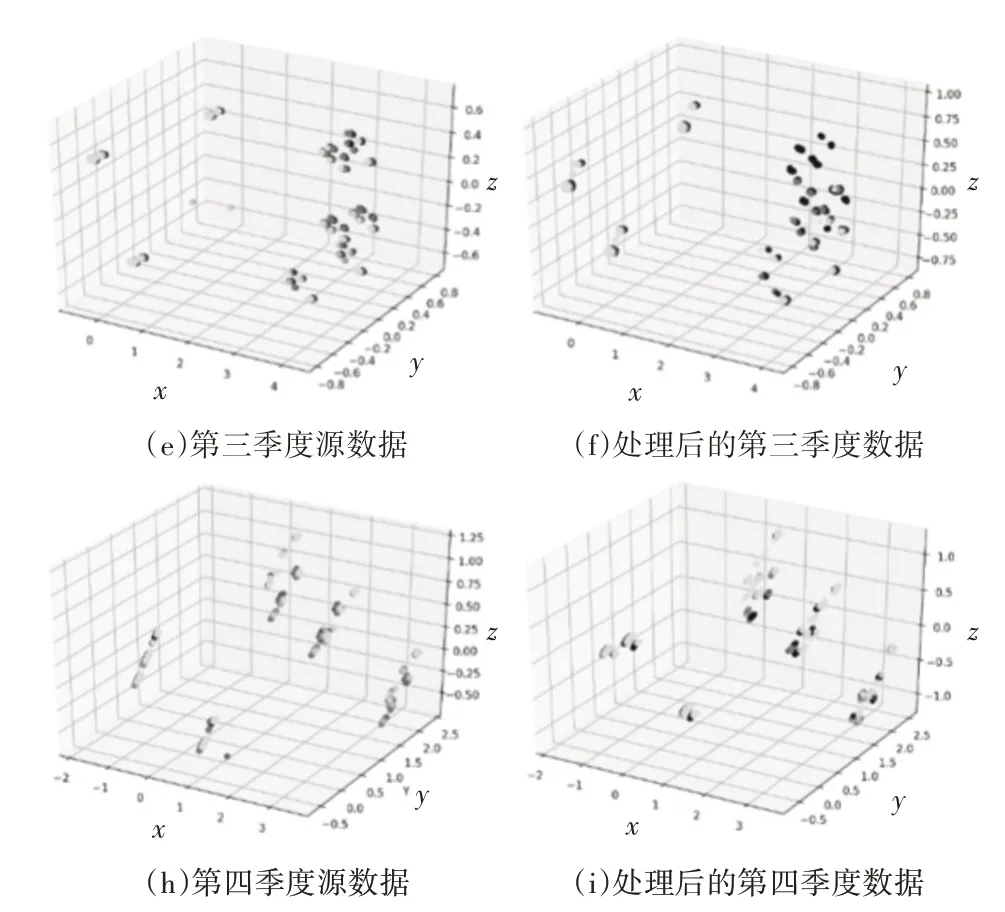
圖3 經過抽樣算法的數據比較圖

表3 GBDT、BP、SVM和SMOE-ENNCSVM模型的分類性能比較

4 結語

本文提供了一個優化的SVM模型，通過使用SMOE-ENN抽樣算法來解決不平衡分類問題，提高了模型的分類精度，從而更好地預測住宅建筑的季度電能消耗。該模型首先針對高維數據稀疏的特點，采用組合式RF-PCA-SVD特征工程算法；其次利用改進的PSO-K均值聚類算法對電能消耗數據進行了季度分析；最后通過采用支持向量機，并將其分類性能與傳統的GBDT、BP分類方法進行比較，證明了SVM與抽樣算法在住宅建筑用電量月度預測中的優越性。這些研究結果為每月在宏觀層面上合理配置整個區域的電力供應提供了參考意見。此外，該模型還有助于改善電網質量，在夏季和冬季的高峰電力季節確保為舒適生活提供穩定的電力供應，可為電力需求側的管理提供可靠的決策依據。