基于無監督深度學習的多波AVO反演及儲層流體識別

孫宇航,劉 洋,3,陳天勝

(1.中國石油大學(北京)油氣資源與探測國家重點實驗室,北京102249;2.中國石油大學(北京)CNPC物探重點實驗室,北京102249;3.中國石油大學(北京)克拉瑪依校區,新疆克拉瑪依834000;4.中國石油化工股份有限公司石油勘探開發研究院,北京100083)

儲層流體識別是地震勘探中的重要環節,主要通過地震波的速度、地下介質的密度和流體因子等參數識別地下的儲層巖性和流體等。流體因子是由地震波速度和地下介質密度組合得到的能夠反映儲層特征的參數,在儲層流體識別中發揮著重要的作用。流體因子的發展先后經歷了加權差類[1-2]、拉梅常數類[3-4]、模量類[5-6]、Gassmann流體項[7-8]和等效流體體積模量[9-10]等階段。等效流體體積模量以其對儲層流體的高敏感性成為現階段的研究熱點。

地震反演是從地震數據中提取流體因子的有效手段,分為疊前反演和疊后反演。相對于后者,疊前反演利用包含更多儲層信息的疊前道集數據,反演結果的分辨率更高。AVO反演是最為常用的疊前反演方法之一。常規AVO反演方法大多只利用縱波道集,只考慮了縱波對流體的敏感性,忽視了橫波對巖性的敏感性。同時利用縱波和轉換波道集進行AVO反演能夠彌補縱波AVO反演的不足,提高反演的精度和穩定性[11-12]。傳統的多波AVO反演大多基于最小二乘或貝葉斯理論構建反演的目標函數[13-15],取得了較好的應用效果。但這種方法的反演精度高度依賴于初始模型的精度,目前大多數實際工區很難建立高精度的初始模型。近年來,受益于計算機計算能力的提升,深度學習方法迅速發展并被應用于疊后波阻抗反演和疊前AVO反演[16-19],取得了較好的結果。深度學習分為有監督和無監督兩種。相對于前者,無監督深度學習方法不需要制作大量高精度的樣本數據,具有更高的實用價值。

目前已有的流體因子反演方法可以分為直接法和間接法。前者直接基于地震記錄反演得到流體因子,后者先基于地震記錄反演得到速度和密度,然后組合得到流體因子。相對而言,直接法不需要進行組合計算,避免了反演過程中產生的累計誤差,反演結果的精度更高。此外,在疊前反演中,密度的反演結果精度較低,利用間接法反演得到的密度會影響組合流體因子的精度。

為了提高儲層流體識別的精度,基于AVO和深度學習理論,本文提出了一種利用縱波和轉換波道集直接反演流體因子的無監督方法。本文主要研究針對砂巖儲層的流體識別。首先,利用砂巖儲層的模型和實際數據分析了各種流體因子對儲層流體的敏感性;然后,基于疊前AVO理論的指導構建了一種多波直接反演流體因子的無監督深度學習方法;最后,將該方法應用于X工區的實際數據反演等效流體體積模量并進行儲層流體識別,從而證明了該方法的反演精度和適用性。

1 砂巖儲層流體因子分析

1.1 基于模型數據分析流體因子的敏感性

利用典型砂巖模型[20]分析不同流體因子對儲層流體的敏感性。砂巖模型參數如表1所示。利用表中數據分別計算泊松比、拉梅常數、縱波模量、Russell流體因子和等效流體體積模量,對計算結果進行歸一化處理并對比,結果如圖1所示,其中,紅色和藍色的面積差異越大,代表流體因子對儲層流體的敏感性越好。由圖1可見,在兩類砂巖模型中,Russell流體因子和等效流體體積模量所在的矩形中紅色和藍色的面積差異較大,其中等效流體體積模量對應的面積差異最大,證明等效流體體積模量對儲層流體具有相對更高的敏感性。

表1 典型砂巖模型參數

1.2 基于實際數據分析流體因子的敏感性

利用X工區實際測井數據分析流體因子對儲層流體的敏感性。考慮到利用模型數據分析時,縱波模量、Russell流體因子和等效流體體積模量對儲層流體的敏感性較高,基于測井數據只計算這3種流體因子。結合已知測井解釋結果,分別做流體因子和孔隙度的交會分析,結果如圖2所示,由圖2可知,縱波模量和Russell流體因子并不能較好地區分含氣砂巖和含水砂巖,等效流體體積模量能夠區分這兩種砂巖,含氣砂巖的取值范圍為-0.7～0.3GPa,含水砂巖的取值范圍為-1.0～0.7GPa。

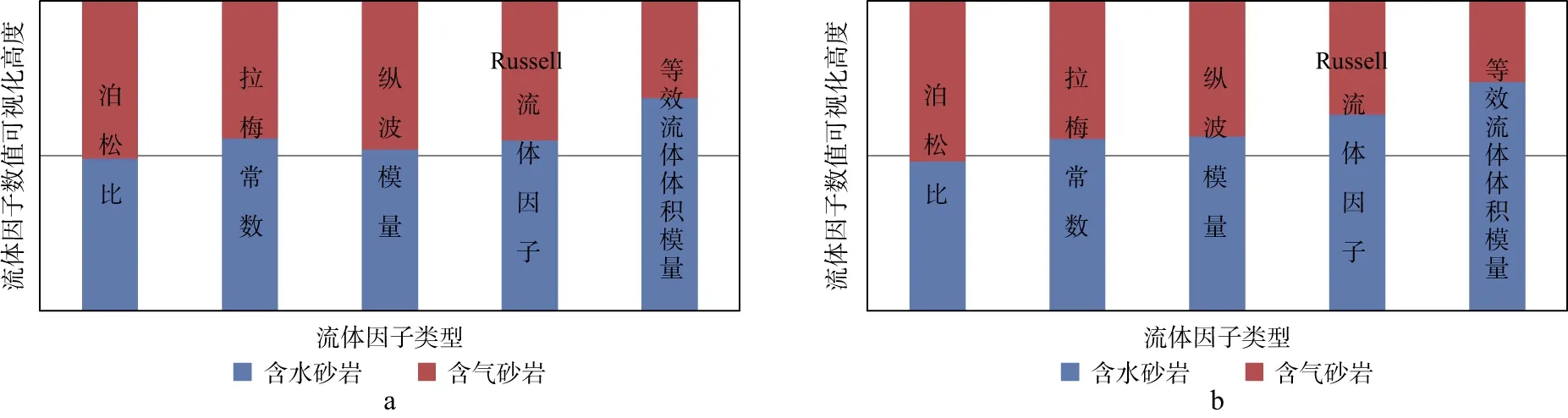
圖1 典型砂巖模型中不同流體因子對比結果a 第一類砂巖模型; b 第二類砂巖模型

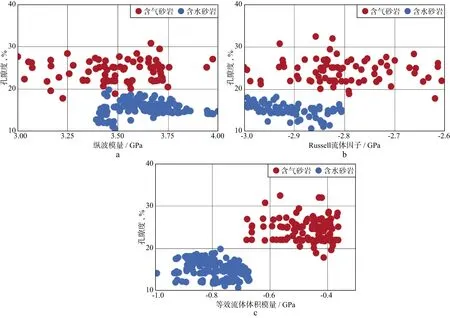
圖2 不同流體因子與孔隙度的交會分析a 縱波模量; b Russell流體因子; c 等效流體體積模量

綜合模型數據和實際數據的分析結果認為,等效流體體積模量對砂巖儲層流體的敏感性更好,本文提出的流體因子反演方法主要針對砂巖儲層進行等效流體體積模量反演。

2 基于無監督深度學習的多波AVO反演方法

2.1 多波AVO反演理論

疊前AVO反演基于褶積模型理論,若不考慮地震子波對地震頻帶的影響,并假設噪聲水平為0,地震褶積模型可以表示為:

d=W*R

(1)

式中:d為地震記錄;W為子波褶積矩陣;R代表反射系數。R可以表示為:

R=Gm

(2)

式中:m表示地層參數組成的矩陣;G表示R與m之間的映射矩陣。一般利用Zoeppritz方程來表示地層參數與反射系數之間的關系,其表達式為:

(3)

式中:θ1和θ2分別代表縱波的反射角和透射角;θ3和θ4分別代表轉換波的反射角和透射角;α、β和ρ分別代表縱波速度、橫波速度和密度;下標1和2分別代表上層和下層介質;R和T分別代表反射系數和透射系數;下標PP和PS分別代表縱波和轉換波。

為了能夠直接反演等效流體體積模量,將公式(3)改寫為由等效流體體積模量直接表示反射系數的矩陣方程。其本質是實現速度與等效流體體積模量之間的相互轉化。目前還沒有直接表示兩者之間關系的表達式,這里引入第3個參數Gassman流體項,Gassmann流體項與速度之間的關系式[7]為:

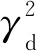
(4)

式中:f代表Gassmann流體項;γd代表干巖石中的縱、橫波速度比;μ代表剪切模量。

Gassmann流體項還可以表示[21]為:

f=GKf

(5)

其中,

(6)

式中:Kf代表等效流體體積模量;Kdry和Ks分別代表干巖石和巖石骨架的體積模量;φ代表孔隙度。

結合臨界孔隙度模型,公式(6)中干巖石的體積模量可以表示為:

(7)

式中:φc代表臨界孔隙度。

將公式(5),(6)和(7)代入公式(4)可以得到縱波速度與等效流體體積模量之間的關系式,即:

(8)

將公式(8)代入公式(3),可以得到直接利用等效流體體積模量表示反射系數的矩陣方程,其中,界面上層的縱波速度α1由界面上層的等效流體體積模量Kf1、孔隙度φ1、密度ρ1和橫波速度β1計算得到;界面下層的縱波速度α2由界面下層的等效流體體積模量Kf2、孔隙度φ2、密度ρ2和橫波速度β2計算得到。

結合公式(1)和公式(2),地震記錄可以表示為:

d=W*Gm

(9)

常規AVO反演的流程如圖2所示。首先,給出初始模型m初;然后,根據公式(9)計算合成地震記錄d合;接著,計算實際地震記錄d實與合成地震記錄d合的L2范數:

L2=‖(d實-d合)‖2

(10)

判斷L2范數是否滿足設定的迭代終止條件,若滿足則此時的m初就是反演結果,若不滿足則更新m初直到L2范數滿足迭代終止條件。傳統的AVO反演方法一般基于最小二乘或貝葉斯理論更新m初,本文基于深度學習更新m初。此外,本文提出的反演方法利用多波疊前道集,目標函數的表達式為:

L2=‖η(dPP實-dPP合)2+(1-η)(dPS實-dPS合)‖2

(11)

式中:η為加權因子,由縱波和轉換波資料的品質決定各自在反演中占的比重。

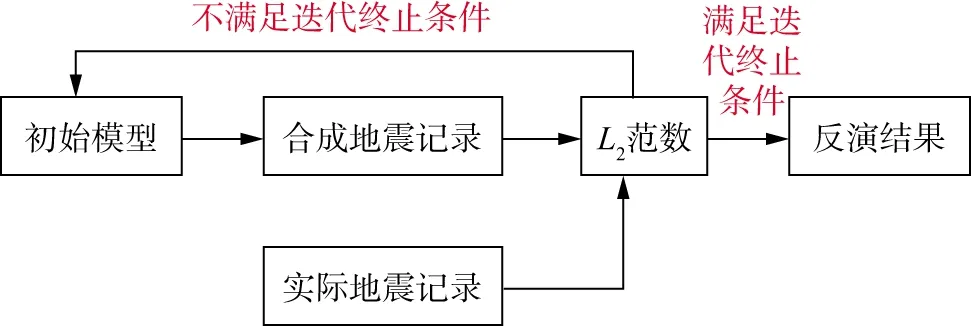
圖3 常規AVO反演流程

2.2 深度學習理論

隨著計算能力的提高,深度學習因其解決問題的泛化能力被廣泛應用于各行各業。深度學習以神經網絡結構為基礎。神經網絡結構分為全連接神經網絡(full connected,FC)、卷積神經網絡(convolutional neural networks,CNN)和循環神經網絡(recurrent neural network,RNN),不同的神經網絡具有不同的特點,適合處理不同的問題。全連接神經網絡是所有網絡的基本結構;卷積神經網絡具有強大的空間特征提取與信息整合能力,適合處理視覺領域的圖像識別分類問題;循環神經網絡具有動態特征和記憶功能,適合處理涉及時序數列的問題。AVO反演中涉及的數據均是連續的,屬于時序數列。因此,基于循環神經網絡構建AVO反演方法具有更大的優勢。循環神經網絡具有一種重復神經網絡模塊的鏈式結構(圖4),包括輸入層、隱藏層和輸出層。圖4中,xt表示t時刻的輸入,ht表示t時刻的輸出。隱藏層中包含了重復的神經網絡模塊。常規循環神經網絡能夠有效地分析和處理較短的時序數列,但不能分析和處理維度過長的時序數列,否則會產生“梯度消失”或“梯度爆炸”的問題。循環神經網絡中的一種改進結構長短時記憶神經網絡(long short term memory network,LSTM)通過“門”的結構(遺忘門、輸入門和輸出門)實現信息的添加或刪除,改善了常規循環神經網絡不能處理較長時序數列的問題。但是,長短時記憶神經網絡的重復結構過于復雜,樣本訓練需要花費大量的時間,因此長短時記憶神經網絡存在很多變體,門控循環神經網絡(gated recurrent unit,GRU)是最為成功的變體之一。門控循環神經網絡利用重置門和更新門代替了長短時記憶神經網絡中的遺忘門、輸入門和輸出門(圖5)。圖5中,xt,ht,rt,zt和mt分別表示t時刻的輸入、輸出、更新門的值、重置門的值和候選值,sig和tanh分別代表sigmoid函數和tanh函數。實驗證明,門控循環神經網絡和長短時記憶神經網絡的識別精度相當,但門控循環神經網絡更易于訓練,效率更高[22]。

對于GRU神經網絡的隱藏層,給定輸入值xt(t=1,2,…,n),t時刻隱藏層的值為:

zt=sig(Wz·[ht-1,xt])

(12a)

rt=sig(Wr·[ht-1,xt])

(12b)

mt=tanh(Wm·[rt·ht-1,xt])

(12c)

ht=(1-zt)oht-1+ztomt

(12d)

式中:ht代表t時刻輸出層的值;ht-1代表t-1時刻輸出層的值;zt代表t時刻更新門的值;rt代表t時刻重置門的值;mt代表t時刻的候選值;W代表權重矩陣;[]表示兩個向量相連接;·是一種矩陣間的計算方法,表示按元素乘。tanh函數表達式為:

(13a)

tanh函數的取值范圍為(-1,1)。sigmoid函數表達式為:

(13b)

sigmoid函數的取值范圍為(0,1)。

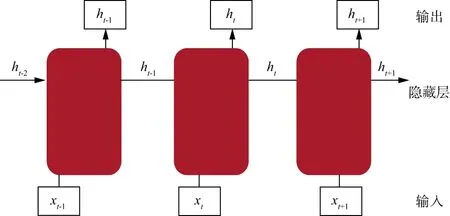
圖4 循環神經網絡中的重復鏈式結構示意

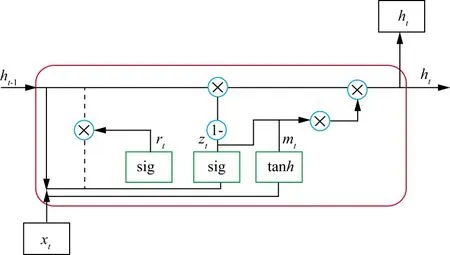
圖5 門控循環神經網絡中鏈式結構示意

GRU神經網絡需要訓練的權重矩陣為Wz,Wr和Wm,它們分別由兩個權重矩陣組合而成,即:

Wz=Wzx+Wzm

(14a)

Wr=Wrx+Wrm

(14b)

Wm=Wmx+Wmm

(14c)

式中:Wzx,Wrx和Wmx分別為輸入值到更新門的權重矩陣、輸入值到重置門的權重矩陣和輸入值到候選值的權重矩陣;Wzm,Wrm和Wmm分別為上一次的候選值到更新門的權重矩陣、上一次的候選值到重置門的權重矩陣和上一次的候選值到候選值的權重矩陣。

2.3 基于無監督深度學習的多波AVO反演方法

結合AVO反演理論和門控循環神經網絡,本文提出了一種基于無監督深度學習的多波AVO反演方法,直接反演等效流體體積模量,其技術流程如圖6 所示。圖6中,紅框內為神經網絡結構,包含1個輸入層、n個GRU隱藏層和1個輸出層。

圖6 基于無監督深度學習的多波AVO反演方法流程

首先,對縱波和轉換波疊前道集進行歸一化處理,歸一化公式為:

(15)

式中:xmin和xmax為xi的最小值和最大值。

然后,將歸一化的疊前道集和初始的權重矩陣輸入到神經網絡結構中,輸出初始的等效流體體積模量、橫波速度和密度,接著利用推導得到矩陣方程,基于神經網絡輸出的初始參數,分別計算縱波和轉換波反射系數,并與地震子波褶積合成疊前道集。

最后,利用公式(11)計算實際和合成道集的L2范數,判斷其是否滿足迭代終止條件,若滿足,則輸出此時的等效流體體積模量,若不滿足,則更新神經網絡結構中的權重矩陣。其中,疊前道集的合成涉及到反射系數的計算,本文用公式(3)和公式(8)計算反射系數并約束神經網絡的訓練,實現等效流體體積模量的確定性反演。采用基于反向傳播理論的訓練方法更新權重系數,其中,利用隨機梯度下降法(stochastic gradient descent,SGD)計算權重梯度。在AVO理論的指導下,該方法不需要制作訓練樣本就能實現等效流體體積模量的預測,是一種典型的無監督深度學習方法。此外,為了提高反演結果的橫向連續性,在輸入疊前道集之前做疊加處理,將相鄰5道或9道的疊前道集疊加為中心道(圖7)。

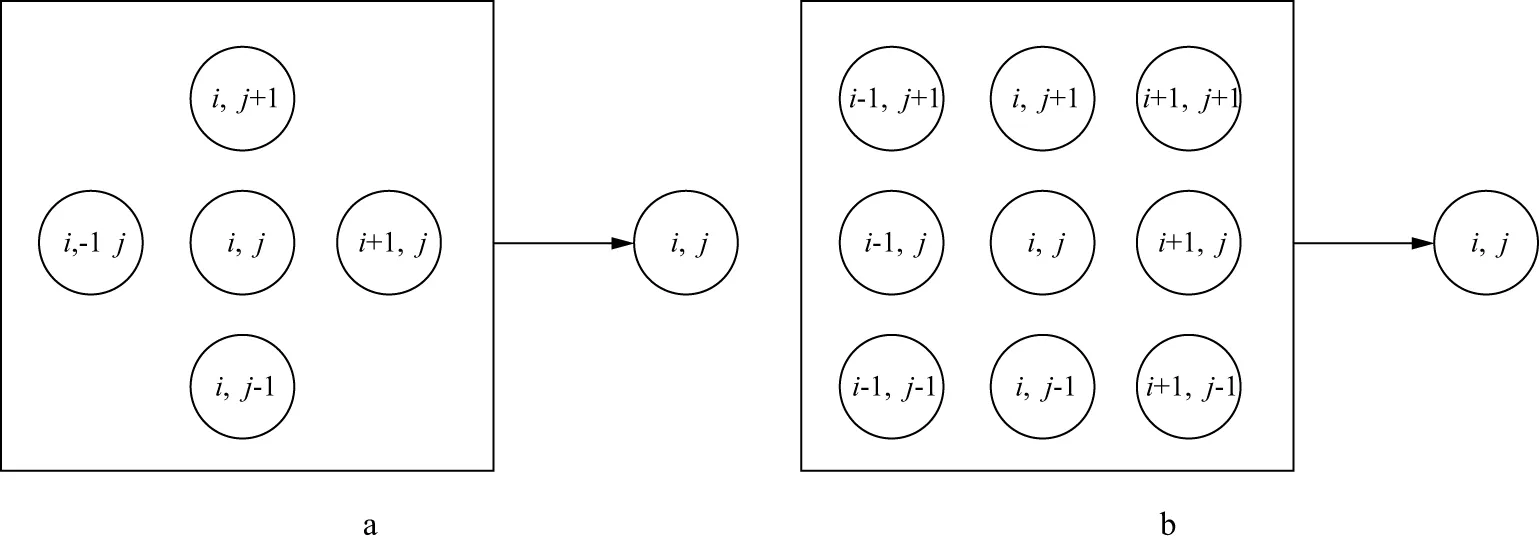
圖7 輸入道集之前的疊加處理示意a 5道疊加; b 9道疊加

3 實際工區儲層流體識別試算

將上述方法應用于X工區,基于縱波和轉換波疊前道集直接反演等效流體體積模量并進行儲層流體識別。

3.1 實際工區介紹

X工區位于我國北部,烴源巖厚度分布不均,單砂體薄,氣水識別不清。工區底圖如圖8所示,包含301條Inline和301條Xline,有縱波和轉換波疊前道集,采樣間隔為4ms,偏移距范圍為75～4275m,間隔為150m。目的層埋深約3000～3170m,轉換到時間域約為1600～1700ms。共有4口測井(A1、A2、A3和A4),每口測井數據中包含縱波速度、橫波速度、密度、孔隙度和含氣飽和度。根據已知測井解釋結果,在1620ms處,4口測井均處于氣藏有利區帶。

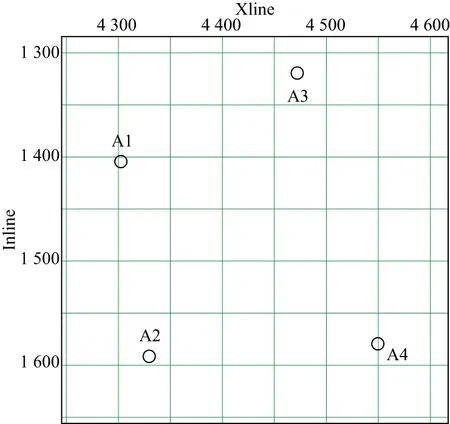
圖8 X工區底圖

3.2 流體因子直接反演及儲層流體識別

在進行等效流體體積模量直接反演之前,需要對數據進行預處理。首先,對道集進行頻譜分析,確定主頻和有效頻帶并進行帶通濾波;然后,進行噪聲壓制以提高信噪比,包括面波、線性干擾和隨機干擾的壓制;最后,在保證足夠信噪比的前提下,再對地震道集進行反褶積以提高分辨率,包括地表一致性反褶積和預測反褶積。將處理好的疊前道集進行歸一化,使其值域處于(0,1),便于在神經網絡結構中的計算;對測井數據進行異常值處理,作為評價反演結果的比對數據。然后進行井震標定,并將縱波和轉換波疊前道集進行偏移距疊加,分別將偏移距75～1325m,1075～2325m,2075～3325m和3075～4275m疊加為偏移距700m,1700,2700和3675m,圖9為過井A1和A2的縱波和轉換波分偏移距道集疊加剖面。考慮到目的層的埋深,將反演的時窗確定為1550～1750ms。AVO反演基于褶積模型,地震子波的提取對于反演結果具有很大的影響。地震子波的提取方法主要分為確定性和統計性提取方法,前者利用測井資料和井旁地震道求取地震子波,依賴于測井資料,得到的子波較為復雜。統計性子波提取方法主要通過地震道自身估計地震子波,與地震數據的相關性更好。利用X工區的地震道集提取統計子波并構建子波矩陣,將偏移距疊加后的疊前道集分別經過圖7b 所示的9道疊加后輸入到構建好的神經網絡結構中,進行訓練和反演。每次輸入一道的偏移距分別為700,1700,2700和3675m的縱波和轉換波道集,輸出一道的等效流體體積模量。經過多次測試,本次反演涉及的神經網絡結構包含1個輸入層、5個GRU隱藏層和1個輸出層,每個GRU隱藏層包括32個神經元,學習步長為0.02。綜合考慮縱波和轉換波道集的品質,通過4口測井井旁道疊前道集的試算,將目標函數中的加權因子η賦值為0.7。

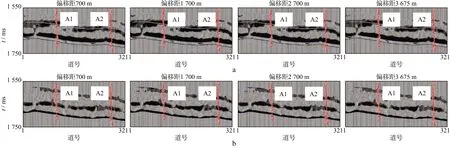
圖9 過井A1和A2的不同分偏移距道集疊加剖面a 縱波剖面; b 轉換波剖面

分別用基于無監督深度學習的多波直接反演、縱波直接反演和多波間接反演方法對工區內4口測井的井旁道地震道集進行等效流體體積模量反演。在運算時間相同的情況下,3種方法對應的反演結果與測井數據曲線如圖10所示。由圖10可知,在4口測井中,反演結果與測井數據的曲線趨于一致。本文利用相對誤差衡量反演結果的精度,相對誤差越小代表反演精度越高。3種方法對應的反演結果與測井數據的相對誤差如表2所示。由表2可知,基于無監督深度學習的多波直接反演方法對應的結果與測井數據之間的相對誤差最小,平均為2.949%;縱波直接反演方法對應的結果與測井數據之間的相對誤差最大,平均為5.369%。圖11展示了反演結果與測井數據之間的絕對誤差,由圖11可知,4口測井的反演結果與測井數據的絕對誤差在0.3GPa內,具有較好的匹配度;多波直接反演對應的絕對誤差最小,在0.1GPa之內,縱波直接反演對應的絕對誤差最大。為了評價反演方法的穩定性,我們將公式(11)的最小化定義為神經網絡的損失函數。圖12展示了多波直接方法在反演過程中的損失函數變化。由圖12可知,在迭代20次左右后,4口測井的損失函數值均接近于0并趨于穩定。綜上所述,基于無監督深度學習的多波直接反演方法具有較高的反演精度和穩定性。

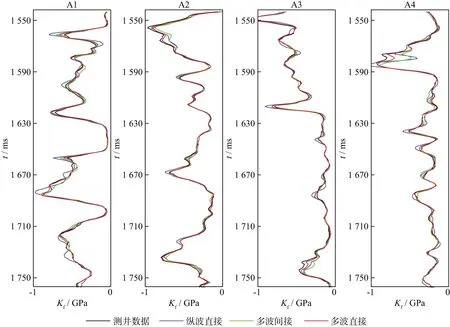
圖10 3種方法的反演結果與測井數據對比

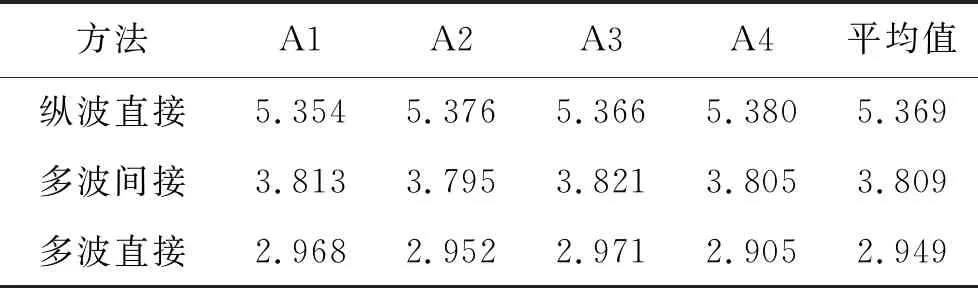
表2 不同方法對應的反演結果與測井數據的相對誤差 %

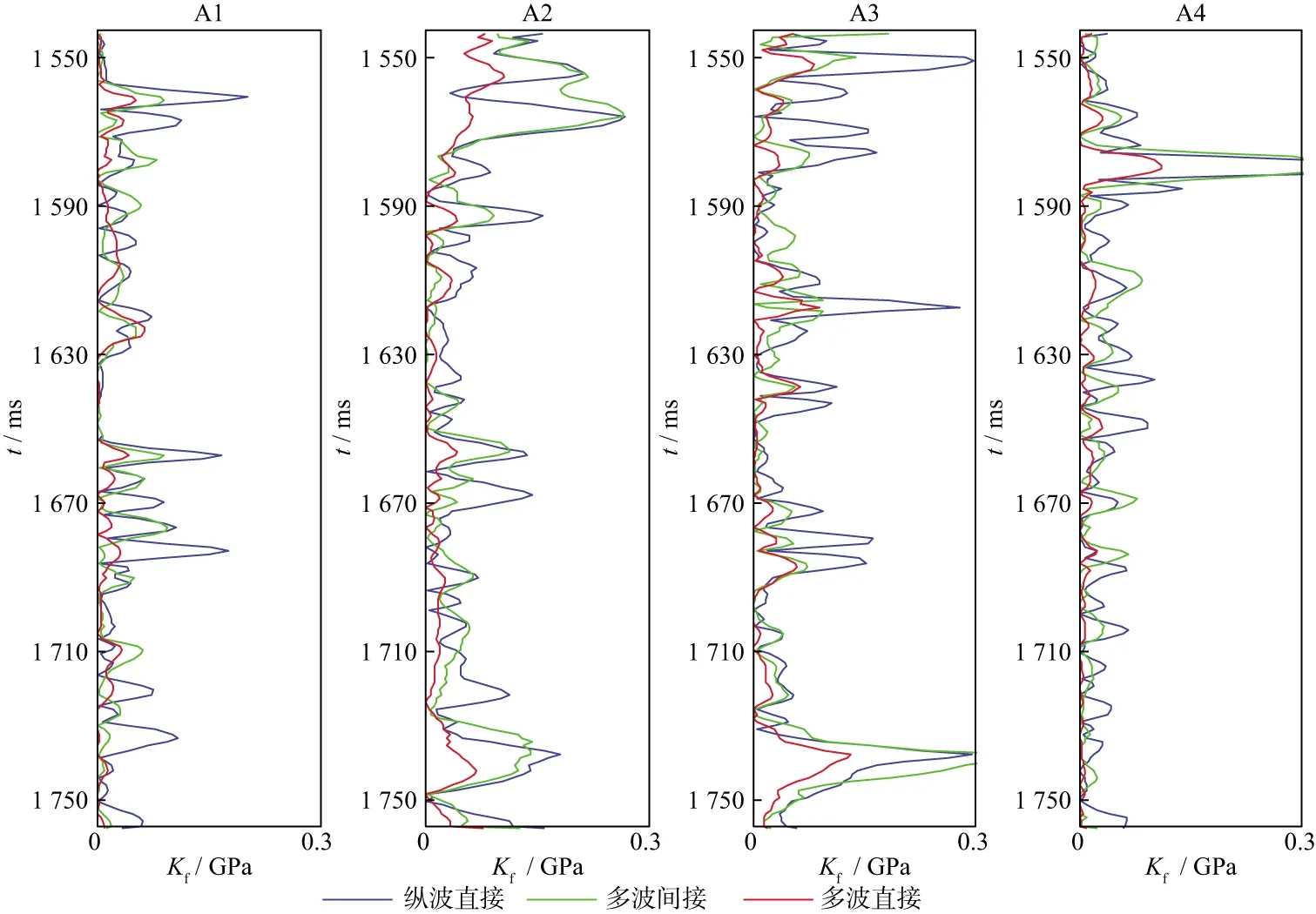
圖11 不同方法的反演結果與測井數據的絕對誤差對比

將多波直接反演方法應用于整個X工區進行等效流體體積模量反演,過井A1和A2的剖面如圖13a 所示,過井A3和A4的剖面如圖13b所示,其中,測井曲線顯示的是含氣飽和度,含氣飽和度較大的區域代表氣層有利區。剖面中紅色、黃色和其它顏色分別代表含氣砂巖、含水砂巖和其它砂巖。由圖13可知,反演剖面連續性良好且與測井曲線吻合度良好。抽取1620ms的時間切片如圖14所示,其中紅色的值域為-0.7～ 0GPa,代表含氣砂巖。由圖14可知,1620ms處,4口測井均處于含氣砂巖儲層,與已知測井解釋結果吻合,驗證了該方法的有效性。

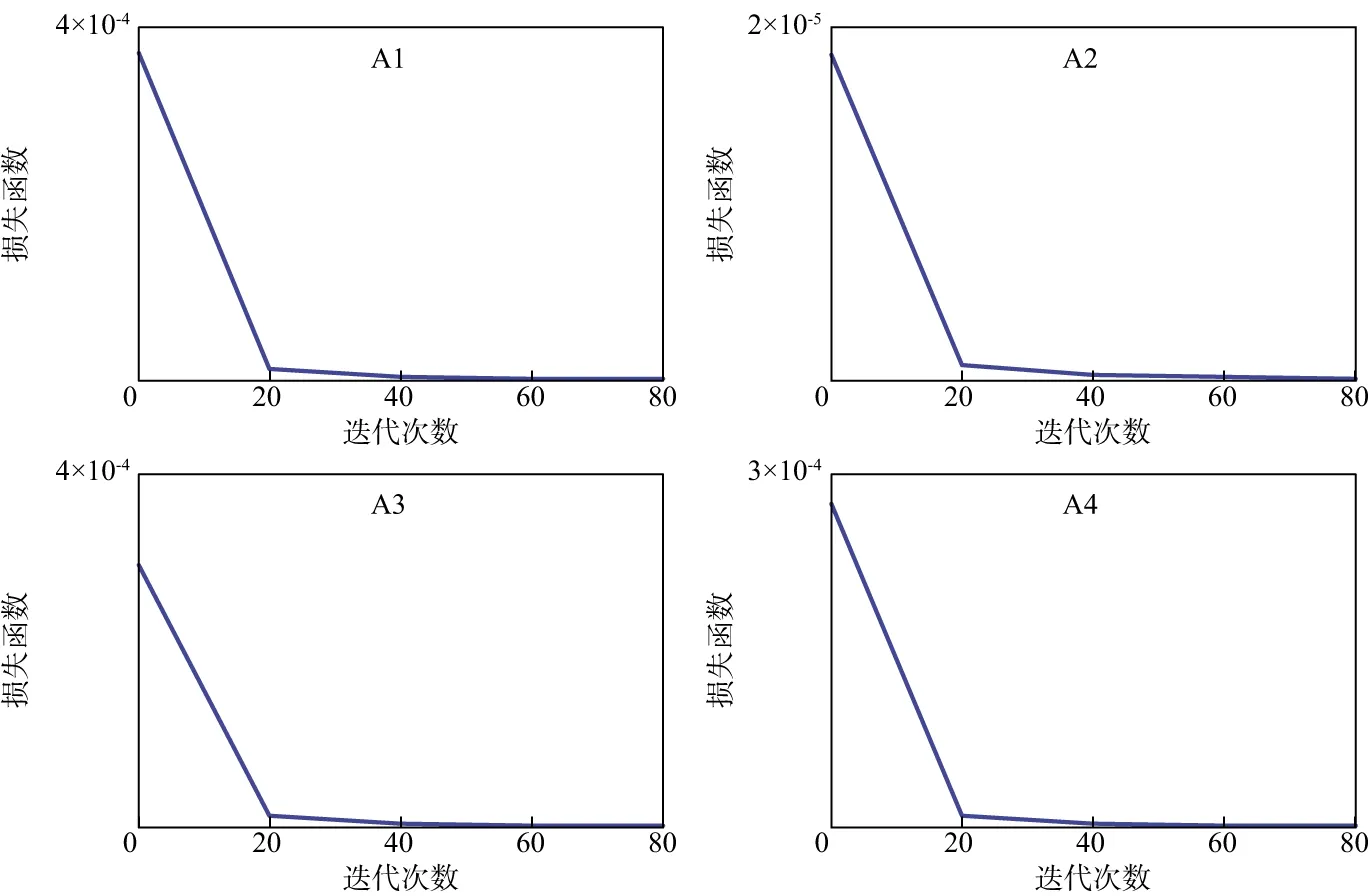
圖12 多波直接方法反演過程中的損失函數變化

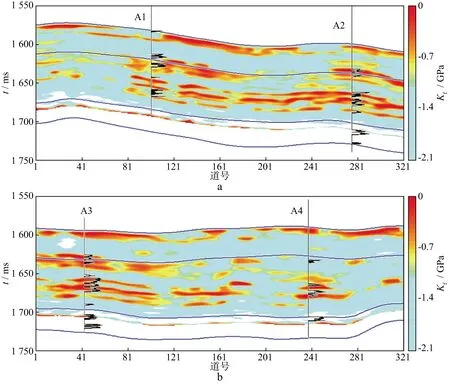
圖13 等效流體體積模量剖面a 過井A1和A2的等效流體體積模量剖面; b 過井A3和A4的等效流體體積模量剖面

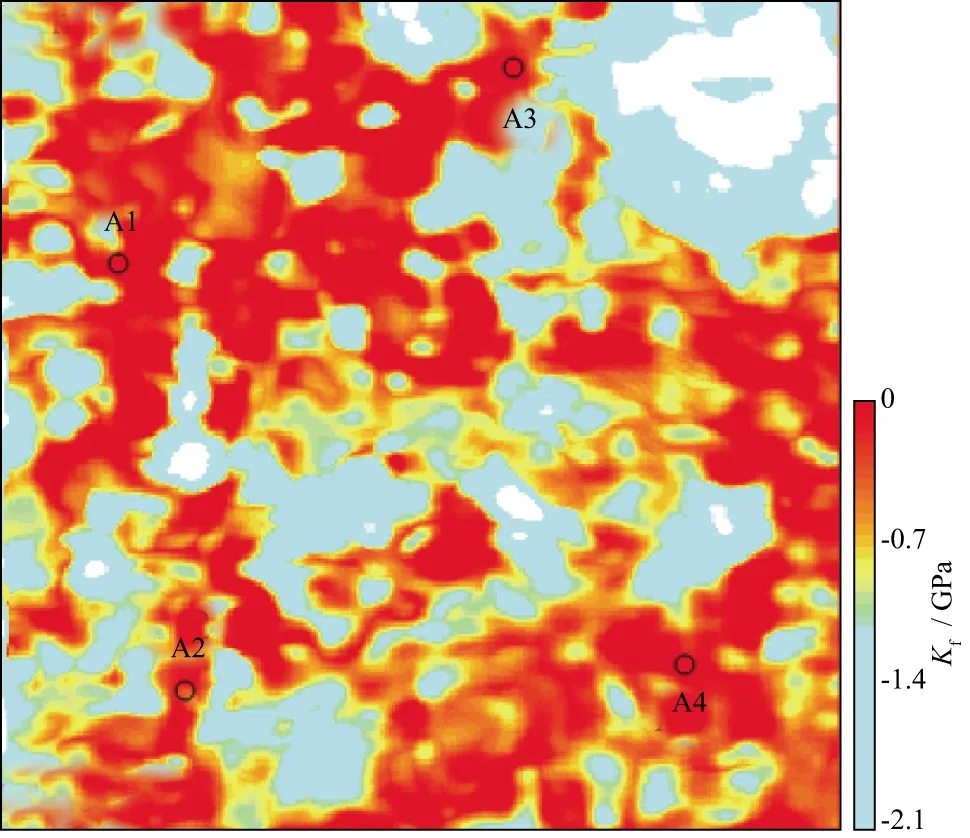
圖14 1620ms等效流體體積模量時間切片

4 結論與認識

本文基于AVO理論和深度學習方法,提出了一種基于無監督深度學習的多波AVO反演方法,直接反演等效流體體積模量。將該方法應用于X工區的實際數據反演以及儲層流體識別,得到以下結論:

1) 對于砂巖儲層,等效流體體積模量對儲層流體的敏感性相對較好,能夠區分含氣砂巖和含水砂巖;

2) 基于無監督深度學習的多波直接反演方法比縱波直接反演和多波間接反演方法的精度更高,多波直接反演的結果與測井數據的相對誤差約為2.949%,絕對誤差小于0.1GPa;

3) 利用基于無監督深度學習的多波AVO直接反演方法反演得到的等效流體體積模量能夠較為精準地識別儲層流體。