彈性波數值模擬中的高斯型混合吸收邊界條件及其GPU并行

王紹文 宋 鵬*②③ 譚 軍②③ 解 闖 毛士博 王倩倩

(①中國海洋大學海洋地球科學學院，山東青島 266100；②青島國家海洋科學與技術實驗室，山東青島 266100；③中國海洋大學海底科學與探測技術教育部重點實驗室，山東青島 266100)

0 引言

地震波正演模擬技術是研究地震波傳播規律的有效手段，并在地震勘探的采集、處理以及反演等各個環節中都有著廣泛的應用。地震波正演模擬必須引入人工邊界界定計算區域，而人工邊界的處理不當，往往會產生虛假反射污染中心波場，從而降低波場模擬的精度，因而人工邊界的處理一直是波動方程數值計算的重要研究內容。

當前的人工邊界處理方法主要有三類。第一類是衰減邊界方法[1-3]。該類方法是在靠近邊界處引入一個衰減區，在衰減區內地震波傳播遵循阻尼波動方程，能量按指數衰減。由于該類方法存在阻尼因子難以確定、計算量大和內存消耗較大等問題，因此應用較少。第二類是完全匹配層(PML)方法。該類方法由Berenger[4]在電磁波數值模擬中首先提出，通過在中心波場計算區域外加上一系列的吸收層、層內引入衰減因子以達到消除邊界反射的目的。王守東[5]、Hastings等[6]、Collino等[7]將PML法成功應用于聲波和彈性波正演模擬。隨后， Komatitsch等[8-9]、熊章強等[10]實現了非分裂PML法；羅玉欽等[11]、楊茜娜等[12]發展了復頻移及多軸復頻移PML法；陳可洋[13]和Wang等[14]提出了基于余弦型和基于高斯型衰減函數的PML方法。PML法現已在地震波數值模擬中獲得廣泛應用，然而為達到更好的吸收效果，PML法往往需要設計幾十甚至上百個匹配層，意味著巨大的計算量和內存消耗，嚴重限制了該方法在大規模波場模擬中的應用。第三類為基于單程波近似的吸收邊界條件。該類方法由Enguist等[15-16]首先提出；Higdon[17-19]提出了一種與其等價的漸進吸收邊界條件，可以設計吸收任意角度的入射波，顯著提升了吸收精度和適應性。然而由于單程波的高階近似會導致邊界條件方程中出現高階的混合時間、空間偏導數項，給數值求解帶來困難，因此常規方法多采用二階邊界條件，但對大角度入射波的吸收效果較差，其整體吸收效果也難以滿足高精度數值模擬的要求。為進一步提升基于單程波近似的吸收邊界條件的效果，宋鵬等[20-21]發展了優化系數的四階吸收邊界條件算法。Baffet等[22]、Hagstrom等[23]以及Potter等[24]也通過引入輔助變量實現了高階吸收邊界條件，但這些算法同樣存在計算過程復雜且計算效率低等問題。

為提升常規基于單程波近似的吸收邊界條件的效果，在不提高階數的前提下，Liu等[25]提出了一種混合吸收邊界條件。該方法在中心波場與邊界之間增加一個過渡區域，通過線性加權使過渡區域內雙程波波場與單程波波場平滑過渡，最終實現了人工邊界的高效吸收。隨后，Liu等[26-27]、任志明等[28]以及Liu等[29]實現了三維聲波及彈性波正演模擬中的混合吸收邊界，Ren等[30]將混合吸收邊界推廣到頻率域數值模擬中，取得了較好的吸收效果。劉學義等[31]將混合吸收邊界用于各向異性介質，Wang等[32]、薛浩等[33]分別將混合吸收邊界應用于逆時偏移和最小二乘逆時偏移。

當前混合吸收邊界已在地震波場正反演延拓中得到廣泛應用，然而，該方法的加權系數仍以線性和指數型[34]為主，未能兼顧內邊界和外邊界的綜合吸收效果，在吸收效率上并沒有達到最優；此外，當前大規模的波場模擬往往借助于GPU并行提高計算效率，但混合吸收邊界差分格式的GPU加速效率遠遠低于中心波場，嚴重影響了整個波場模擬的計算效率。本文提出一種基于高斯型加權系數的混合吸收邊界條件方法，其更能兼顧內、外吸收邊界的吸收效果，具有更高效的整體邊界吸收效率；同時本文還推導了一種更適用于GPU加速的一階Higdon混合吸收邊界條件差分格式，可顯著提升邊界計算的GPU并行效率。

1 基于高斯型加權系數的混合吸收邊界條件

1.1 彈性波數值模擬中混合吸收邊界原理

二維空間中的一階速度—應力彈性波方程[35]可以表示為

(1)

式中：vx、vz分別為水平方向和垂直方向波場速度分量；σxx、σzz、σxz為三個應力分量；ρ為密度，λ和μ為拉梅系數，與縱波速度VP和橫波速度VS關系為

(2)

(3)

式(1)的交錯網格有限差分格式為[36-37]

(4)

(5)

(6)

(7)

(8)

式中：U和W分別表示速度分量vx、vz的離散形式；P、Q和R分別表示應力分量σxx、σzz、σxz的離散形式；Δt、Δx、Δz分別為離散的時間步長、空間水平和垂直網格間隔；i、j、k為空間和時間離散序號；2N為差分階次；am(1≤m≤N)為差分系數，可通過求解下式方程獲取[38]

(9)

應用混合吸收邊界方法進行數值模擬時，整個計算區域被劃分為中心波場區域Ⅰ、邊界過渡區域 Ⅱ 以及邊界區Ⅲ三部分(圖1)，其波場計算流程如下：

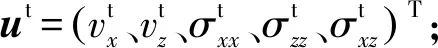
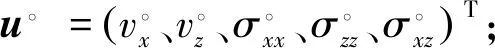
圖1 二維混合吸收邊界條件示意圖

(3)對于M層區域Ⅱ，對雙程波場值和單程波場值進行加權求和得到混合波場

ul=(1-wl)ut+wlu°l=1，2，…，M

(10)

式中wl為加權系數。

而對于區域Ⅱ和區域Ⅲ的單程波場計算，由于二階Higdon吸收邊界條件穩定性較差，通常采用改進的一階Higdon吸收邊界條件[28]，其左邊界方程為

(11)

(12)

則可將一階Higdon左邊界算子表示為[19]

(13)

其差分格式為

(14)

式中與空間位置和網格剖分相關的常量為[19]

(15)

(16)

(17)

其中b為常數，通常取值為0.5。

混合邊界的角點區域需做特殊處理，以左上角速度水平分量為例，其角點差分格式為

(18)

1.2 基于高斯型加權系數的混合吸收邊界

混合邊界通過引入過渡區實現波場混疊壓制邊界反射，過渡區與中心波場相鄰的邊界可稱為內邊界，過渡區的最外層邊界可稱為外邊界，混合邊界的殘余反射通常來自于內邊界和外邊界反射。內、外邊界的殘余反射能量可通過混合加權系數的選取進行調整，常用的線性加權系數和指數型加權系數[34]分別為

(19)

(20)

線性加權系數(圖2黑線所示)在內、外邊界處梯度變化相同，而由于內邊界更靠近內部波場，因此應用線性加權系數的混合邊界其通常會產生較強的內邊界反射；指數型加權系數(圖2綠線所示)在內邊界處變化更加緩慢，使內邊界與中心波場區域得到更好的耦合，因此其內邊界殘余反射得到有效壓制，但另一方面，由于其在內邊界處的變化過于緩慢導致外邊界處的變化過于劇烈，從而易產生較強的外邊界反射。因此一個更為理想的混合邊界條件必須全面考慮地震波在內、外邊界處的綜合邊界反射壓制效果。

鑒于以上分析，本文提出了一種高斯型混合加權系數

(21)

式中α為高斯型權系數的階數，控制內、外邊界處的變化率。大量的實驗證明，當α=2.5時，高斯型混合邊界既能保持穩定性，又可達到良好的邊界吸收效果。

高斯型加權系數(圖2紅線)在內邊界處梯度變化雖然比指數型加權系數稍顯劇烈，但其較線性加權系數已更為平緩；而外邊界處，高斯型加權系數又比指數型加權系數更平緩，較線性加權系數稍劇烈，因此理論上其應有更優的內、外邊界殘余反射綜合壓制效果。

當然，采用混合吸收邊界時，整個邊界的吸收效果還與過渡區層數有關，Liu等[27]證明了當過渡區厚度較小時，混合邊界易不穩定，并且考慮到為追求更高精度的波場模擬效果，當前數值模擬時通常大多采用20層以上的混合吸收邊界。因此本文將以20層和30層為例討論高斯型混合加權系數的吸收效果。

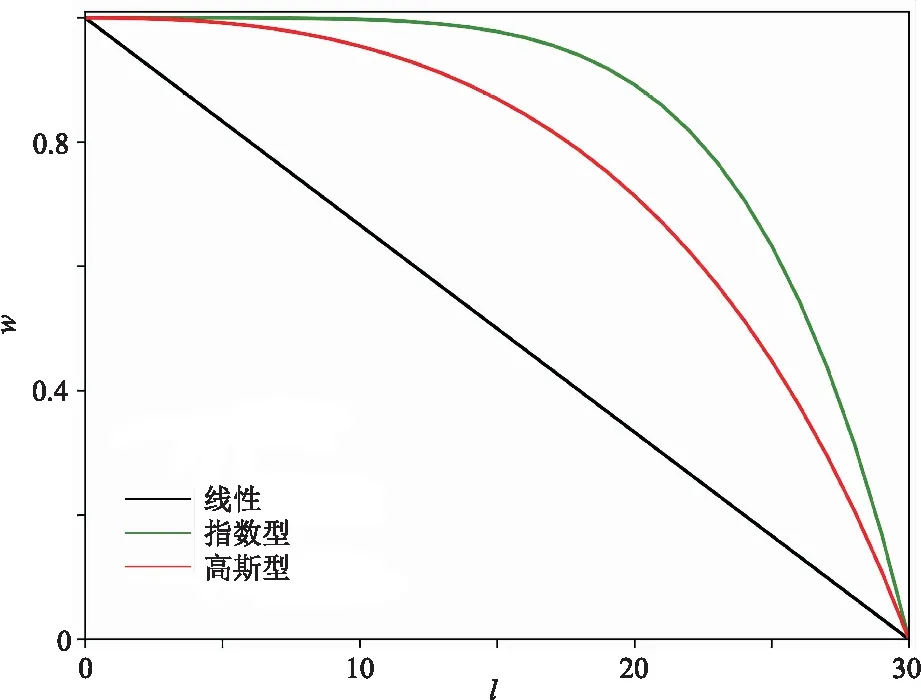
圖2 線性、指數型、高斯型加權系數變化曲線

1.3 常速模型數值模擬實驗

為驗證本文提出的高斯型混合吸收邊界條件的吸收效果，本文設計3200m×3200m、VP=4000m/s、VS=2000m/s、ρ= 2100kg/m3的均勻介質模型。縱、橫向空間網格間距均為8m，時間步長為1ms，差分格式精度為空間10階。震源位于模型中心，采用主頻為25Hz的Ricker子波加載于速度垂直分量上，記錄長度為2s。

應用20層混合吸收邊界得到1s時刻的vx、vz分量波前快照如圖3所示，波前快照的水平和垂直切片(位置見圖3紅色虛線)如圖4所示。應用30層混合吸收邊界得到1s時刻的vx、vz分量波前快照如圖5所示，波前快照的水平和垂直切片(位置見圖5紅色虛線)如圖6所示。

由圖3～圖6可見，無論是20層還是30層吸收邊界，對于vx、vz分量，線性加權系數其波前快照中仍存在較強的內邊界殘余反射(圖3左、圖5左箭頭所示)，指數型加權系數其波前快照中則存在著明顯的外邊界殘余反射(圖3中、圖5中箭頭所示)，而高斯型加權系數的波前快照中無明顯邊界殘余反射波。

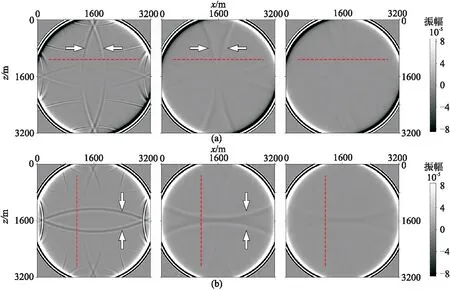
圖3 20層混合吸收邊界不同加權系數的1s時刻vx分量(a)、vz分量(b)波場模擬快照對比 左：線性；中：指數型；右：高斯型

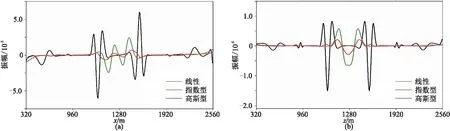
圖4 20層混合吸收邊界不同加權系數的1s時刻vx分量(a)、vz分量(b)波場模擬切片對比

圖5 30層混合吸收邊界不同加權系數的1s時刻vx分量(a)、vz分量(b)波場模擬快照對比 左：線性；中：指數型；右：高斯型

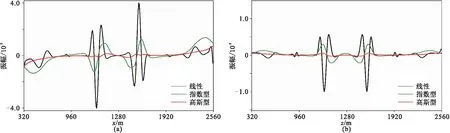
圖6 30層混合吸收邊界不同加權系數的1s時刻vx分量(a)、vz分量(b)波場模擬切片對比

2 適用于GPU加速的一階Higdon混合吸收邊界條件差分格式

當前大規模的波場模擬往往借助于GPU并行提高計算效率。但應用于大規模波場模擬的混合邊界差分格式的GPU加速比遠遠低于中心波場計算的GPU加速比，嚴重影響了整個波場模擬的計算效率。本文推導了一種新的混合邊界差分計算格式，可顯著提高邊界計算的GPU加速比。

2.1 適用于GPU并行的混合吸收邊界差分格式

由式(14)可知，基于常規混合吸收邊界差分格式進行GPU并行時，由于每層邊界上k+1時刻的波場值計算都要用到該層內側點k+1時刻的波場值，所以應用GPU計算邊界時無法同時啟動大量的線程實現邊界各點值的同時計算，無法實現高效的GPU并行。為了解決常規邊界差分格式中需要由內向外依次計算、無法實現GPU高效并行的問題，本文推導了一種新的邊界條件差分格式，具體推導過程如下(以左邊界和左上角點為例)。

為避免邊界區域計算時，差分格式的右側不出現k+1時刻項，將時間偏導數和水平方向空間偏導數分別表示為

(22)

(23)

則可將一階Higdon邊界算子表示為

(24)

(25)

對于左上角點，可通過上邊界和左邊界的加權平均得到

(26)

對比式(14)與式(25)可知，當計算k+1時刻波場值時，本文推導的差分格式只需用到已計算出的k時刻波場值，因此同一時間切片內所有網格點可同時計算，能實現GPU的高效并行加速。

在常規混合吸收邊界算法中，由于第l層邊界計算與第l+1層邊界計算存在計算先后順序關系，過渡區Ⅱ中的混合波場計算需要由最內側開始逐層向外進行，因此同一時間層內，前者需多次啟動邊界計算核函數(與邊界層數相當)，且每次核函數只能計算本吸收層內的網格點數，嚴重降低了GPU的加速效率。基于本文差分格式的混合吸收邊界算法，只需一次啟動和計算邊界計算核函數，可實現所有吸收層內的所有網格點的同時計算，更適合于大規模波場模擬的GPU高效并行計算。

2.2 常速模型數值實驗

應用上述均勻模型和模擬參數，驗證本文推導的混合吸收邊界差分格式的正確性。20、30層常規差分格式與本文差分格式vx、vz分量波前快照如圖7、圖8所示。

由圖7、圖8可以看出，在邊界層數相同的條件下，兩種差分格式的混合吸收邊界均能有效壓制邊界反射。

圖7 不同邊界差分格式的20層混合吸收邊界數值模擬的0.6(左)、1.0(中)和1.4s(右)時刻波前快照對比(a)常規差分格式vx分量； (b)常規差分格式vz分量； (c)本文差分格式vx分量； (d)本文差分格式vz分量

為評估兩種差分格式的計算效率，本文基于RTX-2080Ti-11GB的GPU應用上述均勻模型進行測試，結果如表1所示。

由表1可見，若采用20層邊界，本文邊界差分格式計算效率為常規差分格式3.25倍；若采用30層邊界，本文邊界差分格式計算效率為常規差分格式4.34倍，因此本文差分格式更適于大規模波場模擬的GPU高效并行計算。

表1 兩種邊界差分格式正演模擬計算效率對比

圖8 不同邊界差分格式30層混合吸收邊界數值模擬的0.6(左)、1.0(中)和1.4s(右)時刻波前快照對比(a)常規差分格式vx分量； (b)常規差分格式vz分量； (c)本文差分格式vx分量； (d)本文差分格式vz分量

3 復雜模型實驗

本文截取了Marmousi模型的一部分(圖9)進行正演模擬測試。該模型尺寸為3000m×3000m，縱橫波速比為1.73，常密度為2100kg/m3。數值模擬中，橫向和縱向網格間隔分別為5m和4m，時間步長為0.4ms。震源采用加載于vz分量上、主頻為25Hz的Ricker子波，位于(1500m，4m)處。

未加吸收邊界、常規差分格式的高斯型混合吸收邊界(30層)和本文差分格式的高斯型混合吸收邊界(30層)模擬的1.4s時vx、vz分量的波前快照如圖10所示。由圖可見，未加吸收邊界的波場中有明顯的強邊界反射，而無論采用常規邊界差分格式還是本文差分格式的30層混合吸收邊界，均可有效吸收邊界反射，表明基于高斯型混合加權吸收邊界能夠適應于復雜構造模型的邊界處理。

基于單卡GPU(型號：RTX-2080Ti-11GB)，常規差分格式的高斯型混合吸收邊界的部分Mar-mousi模型計算時間為16.6335s，本文差分格式計算時間為5.3510s，可見本文差分格式的計算效率是常規格式的3倍以上，說明本文的邊界差分格式更適合大規模數值模擬的GPU高效并行。

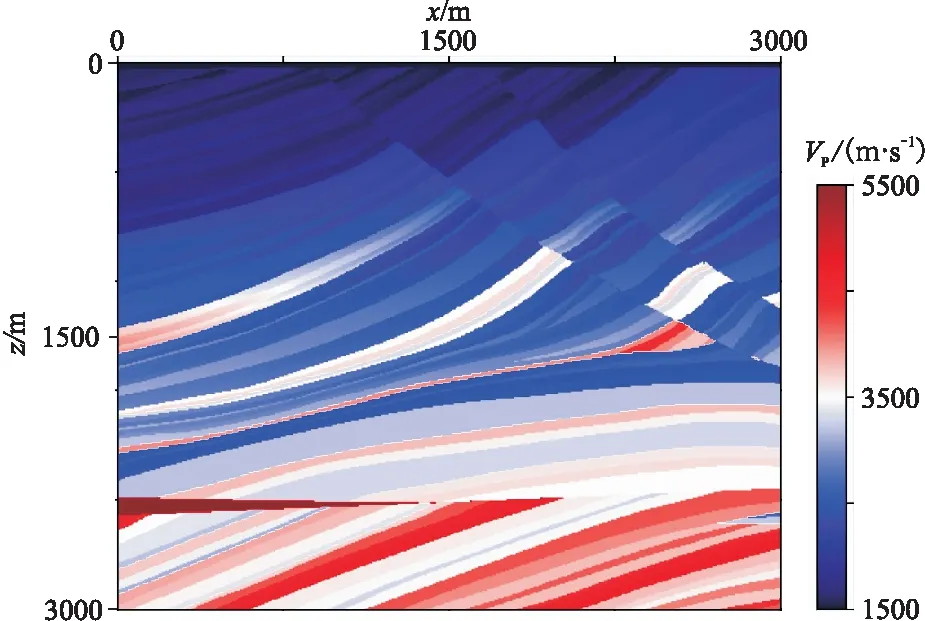
圖9 部分Marmousi縱波速度模型

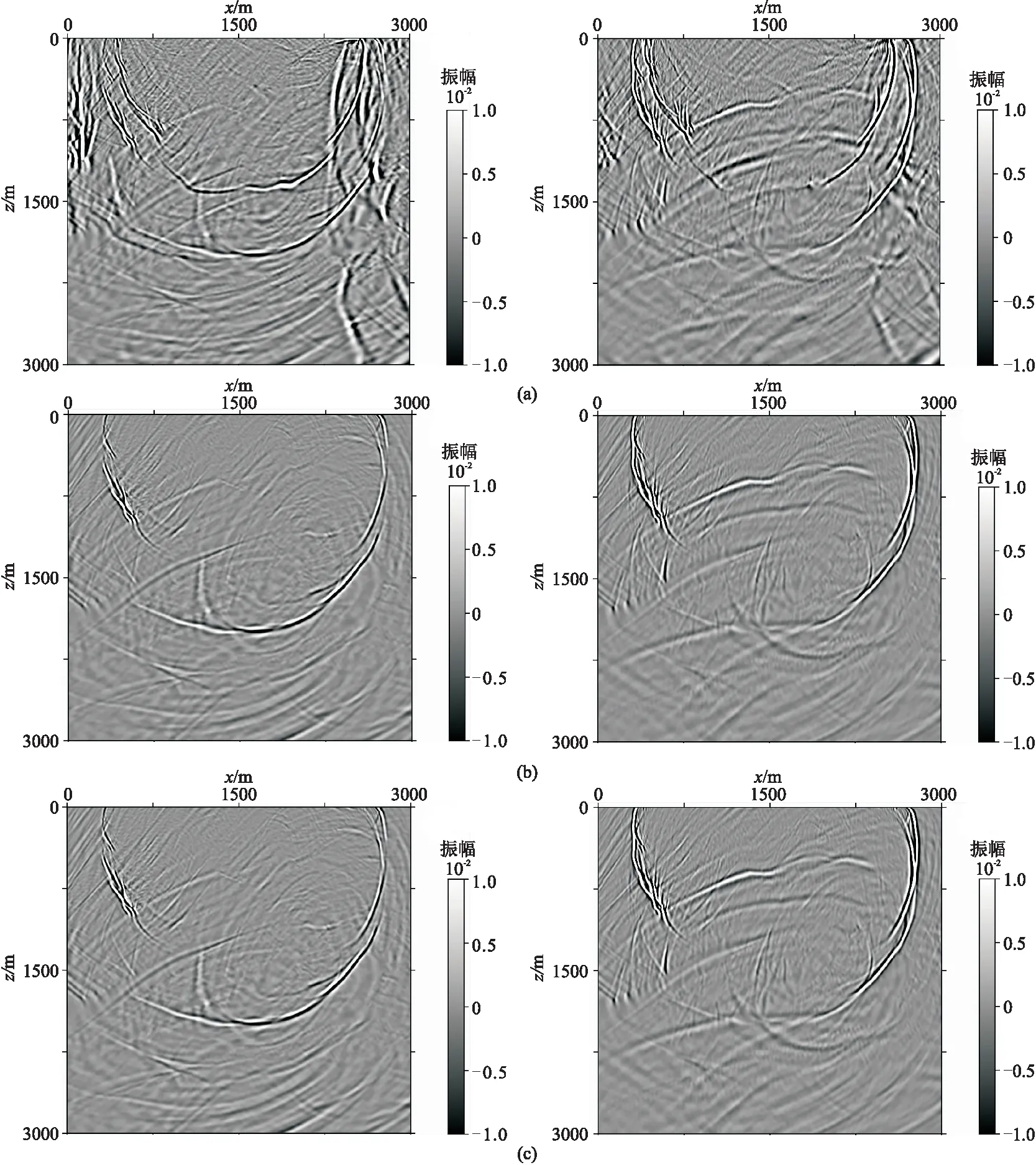
圖10 Marmousi模型不同邊界模擬的1.5s時刻的vx分量(左)、vz分量(右)波場快照(a)不加邊界； (b)常規差分格式的高斯型混合吸收邊界； (c)本文差分格式的高斯型混合吸收邊界

4 結論

本文在系統分析線性混合邊界和指數型混合邊界殘余反射形成機制的基礎上，提出了一種能兼顧內外邊界吸收效果的高斯型混合吸收邊界條件。在此基礎上，推導了更適用于GPU加速的一階Higdon混合吸收邊界條件差分格式及相應的角點計算差分格式。模型實驗結果表明，高斯型混合吸收邊界能更有效地壓制內邊界和外邊界反射，比線性和指數型混合吸收邊界具有更高的吸收效率，適用于復雜構造模型的邊界處理；本文推導的邊界及其角點的邊界差分格式，GPU并行的計算效率更高，更適用于大規模彈性波場數值模擬。

將本文提出的混合吸收邊界算法推廣至三維彈性波數值模擬及逆時偏移和全波形反演，是今后的研究方向。

十分感謝中國海洋大學地球探測軟件技術研發團隊提供了資金和軟、硬件支持，以及團隊成員提供了建設性意見。