過冷度影響海水結冰形狀與速度的相場模擬

白 旭， 楊蘇杰

(江蘇科技大學，船舶與海洋工程學院，江蘇 鎮江，212003)

近年來，隨著全球氣候變暖，北極地區冰川消融，北極航道得到開發.但是，由于北極地區特殊的地理環境，船舶在北極航行時極易受到結冰的影響[1].已有的針對船舶結冰的研究大多集中在宏觀層面，即不同氣候條件下，海洋結構物各部位產生的結冰以及結冰造成的影響，結冰的原理也主要來自于經驗公式和觀測結果總結，很少有對其產生原因和微觀機理的分析[2-4].通過研究海水結冰的微觀機理，用實際環境參數來模擬海水結冰過程，可以得到更加真實的冰晶生長情況，為過冷條件下海水飛沫結冰提供微觀理論基礎.針對海水的微觀結冰過程，現在國內相關研究主要集中在單個晶核的凝固現象，而在實際情況下，外界環境所導致的結冰幾乎都是多晶核條件下的結冰.因此，本研究不僅會分析過冷度對海水結冰的影響，同時會涉及多晶核條件下的海水凝固情況.研究水滴凝固的微觀機理的重點在于追蹤冰晶凝固時固液界面的移動，而通過引入相場法，建立溫度、相場等多個微分方程，可以將真實環境條件引入模擬計算，模擬固液擴散界面，從而得到冰晶的生成演化過程[5-6].

相場法最早是在20世紀80年代由Collins等提出[7].1993年，Kobayashi首先建立了關于相場和溫度的相場模型，在考慮各向異性的情況下，模擬了金屬凝固時的枝晶生長[8].Wheeler等[9]模擬了Ni的凝固過程，并提出了二元合金的相場方程，即WBM模型，并將相場模擬與實際物理量聯系起來，定量分析參數對凝固現象的影響.Fan 等[10]基于平均濃度場和熱、質及動量輸運現象，模擬了蛋白質溶液在冷凍過程中蛋白質的分離與重分布.Yang等[11]使用冰模板，考慮石墨烯再分配和冰晶的各向異性，模擬了在水凍結時石墨烯氣凝膠的形成過程.

國內學者對于相場模型的研究也有一定進展.楊燕等[12]利用Wheeler模型模擬了過冷條件下不同過冷度對冰晶生長的影響.朱昌盛等[13]基于KKS模型模擬了在等溫和不等溫兩種條件下潛熱對二元合金凝固的影響.于艷梅等[14]對單相和二元合金分別進行相場模擬，分析空間尺度、外界噪聲及各向異性等參數對過冷熔體凝固過程的影響.韓端鋒等[15-16]分別使用Kobayashi模型和Wheeler模型，模擬了單晶核條件下純水和海水的凝固過程，定量分析了外界參數對冰晶凝固的影響.

針對船舶結構的宏觀結冰與微觀機理的研究方面，Ryerson等[17]利用船舶切割下的冰晶進行研究，將結冰的宏觀現象和微觀機理相聯系，得到了結構結冰的物理性質和結冰部位的微觀分析.Singh等[18]利用分子動力學定量研究了光滑粗糙表面上過冷水滴的行為，分析了在粗糙表面上凝固溫度和液滴黏附功與粗糙度之間的聯系.Sultana等[19]利用數值模擬分析了單個鹽水滴在撞擊極冷表面后的相變情況，探討了液相率、鹽度等物理性質對液滴凍結的影響.

本文基于Wheeler相場模型，運用有限差分法，對不同過冷度下海水結冰情況進行模擬，研究過冷度對海水凝固時冰晶生長形狀和速度的影響，為船舶結冰預報提供理論和技術支持.

1 Wheeler相場模型理論

1.1 相場方程

相場法以金茲堡-道朗方程為研究基礎[20]，通過引入相場參數φ來表示固液界面的移動.當φ=1時表示固相，φ=0時表示液相，0<φ<1時表示固液界面，通過數值的變化來實現對固液界面的跟蹤.

金茲堡-道朗自由能方程為

(1)

式中：f(φ,T)和β(T)分別為自由能密度函數和熱力學驅動力函數，β(T)<1/2；W為單位體積能量；p(φ)為固相分數，1-p(φ)為液相分數，p(φ)=φ3(10-15φ+6φ2).

相場方程為

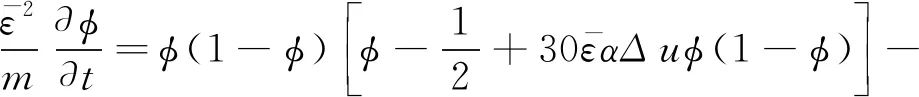
(2)

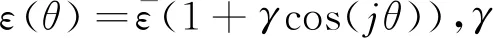
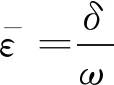
其中：δ為特征長度；ω為長度參考尺寸；μ為界面遷移率；σ為表面能；TM為海水凝固點；K為熱擴散系數；L為單位體積潛熱；cp為比熱容；ΔT為溶液過冷度，ΔT=TM-T0，T0為溶液初始溫度.

溫度場方程為

(3)

式中：p(φ)的導數p′(φ)=30φ2(1-φ)2；無量綱溫度u=(T-TM)/(TM-T0).

Wheeler相場將實際物理量與相場參數相結合，因此在計算中，應該使用實際物理參數進行計算.但是為了將界面厚度控制在可計算范圍內，取ω為2.7×10-4cm，將其無量綱化，實際界面厚度等于無量綱界面厚度與長度參考尺寸的乘積，網格間距也按照同樣方法進行換算.

1.2 溶質場方程

在模擬海水凝固時，將海水視為水和鹽的二元溶液，相比于一元溶液，二元溶液需要考慮溶質的影響.溶質對凝固的影響主要有兩種方式，一種是引入溶質對過冷度的影響，另一種是在方程中添加濃度項[21].本文通過引入過冷度變化，來實現溶質擴散對溶液凝固的影響.溶質場方程為

(4)

(5)

式中：C為海水中鹽的摩爾分數，海水中鹽的質量分數約為3.5%，則鹽的摩爾分數為0.011；k0為平衡分配系數；D為無量綱擴散系數；Ds為固相擴散率；Dl為液相擴散率.

模擬過程中，計算域內的過冷度受到溶質濃度影響，實時過冷度為

(6)

式中：mL為液相線斜率；C0為溶液初始質量分數.

1.3 參數取值

本文所取物性參數均按照質量分數為3.5%的海水溶液選取[15]，具體取值如表1所示.

表1 海水溶液物性參數Tab.1 Physical properties of seawater solution

2 數值求解與可靠性驗證

在得到相場模型后，需要對其進行數值求解.有限差分法原理簡單，易于編程，因此本文采用有限差分法來求解控制方程.有限差分法是將要求的函數在時間和空間上離散，用差分代替微分，并用離散的值來表示函數在計算域內的變化，結合初始條件和邊界條件，求出函數在計算域內各網格節點的值.

2.1 有限差分法及離散方式

求解相場控制方程時，空間離散采用中心差分方法，時間離散采用顯式差分方法.另外，對于方程中出現的拉普拉斯算子，采用九點差分方法進行離散：

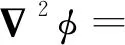
φi+1, j+1+φi-1, j-1+φi-1, j+1+φi+1, j-1]/

[3(Δx)2]

式中：Δx、Δy為網格間距；Δt為時間步長.對于溫度場和溶質場方程，采用與相場方程同樣的差分格式.

在計算域內，為了滿足計算精度，保證計算結果收斂，需要同時考慮相場、溫度場及溶質場.計算域內的時間步長和空間步長需滿足以下條件

(7)

(8)

2.2 初始條件和邊界條件

本文計算域設置為正方形，網格數設置為1 500×1 500，網格間距Δx和Δy在無量綱化后均為0.03，時間步長Δt=0.000 1 s.在計算域內，按照正方形設置4個初始晶核，晶核半徑為R.初始晶核距離計算域邊界均為50R，晶核之間距離為50R.晶核分布如圖1所示.

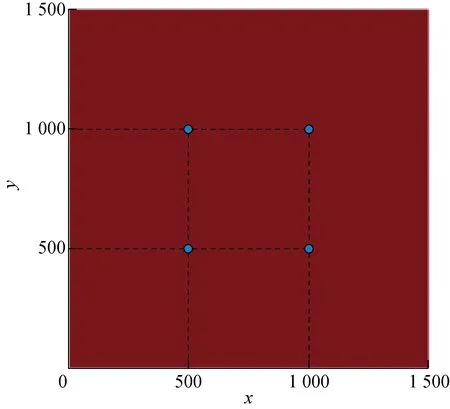
圖1 初始晶核大小與位置Fig.1 Initial nuclei size and position

晶核外相場參數φ設為1，無量綱溫度u為-Δ，質量分數C為C0，具體晶核位置和條件設置如下式：

(x-500)2+(y-500)2≤R2時，

φ=0,u=-Δ,C=C0

(9)

(x-1 000)2+(y-500)2≤R2時，

φ=0,u=-Δ,C=C0

(10)

(x-500)2+(y-1000)2≤R2時，

φ=0,u=-Δ,C=C0

(11)

(x-1 000)2+(y-1 000)2≤R2時，

φ=0,u=-Δ,C=C0

(12)

相場、溫度場和濃度場均采用Neumann邊界條件，即

(13)

2.3 模擬冰晶與自然冰晶的對比

為了得到海水結冰的過程及規律，首先對冰晶凝固過程進行模擬，并將其和實際自然條件下生成的冰晶進行對比.使用上文設置參數，網格劃分為500×500, 模擬時間為7 500Δt，得到結果如圖2所示.冰晶在凝固時，先由晶核發展為冰盤，隨后主要沿著6個方向發展，形成主枝，主枝之間的夾角約為60°，主枝隨后向兩側長出側枝和多次分枝，最終形成六角冰晶.通過比較模擬的冰晶形狀和現實的冰晶形狀[22]，發現實驗結果吻合良好，可以進行進一步模擬計算.

圖2 模擬冰晶與實際冰晶形狀對比Fig.2 Comparison of simulated ice crystal and actual ice crystal

3 過冷度對晶核生長形狀及速度的影響

3.1 過冷度對晶核生長形狀的影響

根據凝固理論，過冷度是液體凝固的驅動力，在冰晶的形核和生長中起重要作用.本文通過分析冰晶形貌、生長速度以及枝晶間距來描述過冷度對冰晶生長的影響.

選擇0.80、0.85、0.90、0.95及1.00這5個不同無量綱過冷度作為模擬溫度，各無量綱過冷度對應實際過冷度分別為 -63.34、-67.30、-71.26、-75.22 及 -79.18 K.總模擬時間為 7 500Δt，模擬結果如圖3所示.

從圖中可以看出，當Δ=0.80時，枝晶生長緩慢，僅有少量二次分枝，枝晶直到模擬結束未發生交匯，仍然是晶核各自發展.隨著無量綱過冷度的增大，枝晶生長速度加快，主枝變粗，分枝數量增加，但枝晶之間仍未發生交匯.當Δ=0.90時，生長速度進一步增加，出現二級以上多次分枝，枝晶在模擬過程中出現交匯.交匯后主枝停止生長，分枝未受影響，繼續向外生長.Δ=1.00時，粗大的主枝占據了極大的空間，使得分枝數量減少.當主枝交匯后，主枝逐漸變粗，分枝繼續發展，逐漸填滿晶核間空隙，幾乎形成冰盤.

圖4為各過冷度下分別模擬 10 000Δt得到結果.通過比較各過冷度凝固結果可以看出，在同時存在多個晶核時，過冷度越大，枝晶就越早接觸，枝晶內部空隙就越小，以至于最終完全接觸，內部不再存在空隙.過冷度較小時，橫向與縱向主枝有粗細差別，橫向主枝較粗，而過冷度較大時，橫向與縱向主枝粗細基本相同.

圖3 冰晶凝固過程Fig.3 Solidification process of ice crystals

圖4 10 000Δt各無量綱過冷度凝固結果Fig.4 Solidification results of each dimensionless undercooling at 10 000Δt

3.2 過冷度對晶核生長速度的影響

為了定量分析過冷度對海水凝固的影響，使用枝晶尖端生長速度vtip來描述冰晶生長情況，枝晶尖端生長速度與無量綱時間和無量綱過冷度之間關系如圖5所示.

圖5(a)為無量綱過冷度為0.8時，尖端速度隨無量綱時間變化情況.根據計算結果，枝晶在生長過程中較為穩定，尖端速度在開始時較大，隨后慢慢減小，近似呈正弦函數波動.枝晶尖端速度隨無量綱過冷度的變化如圖5(b)所示，在無量綱過冷度從0.8增至1.0的過程中，枝晶尖端平均速度分別為0.288、0.360、0.432、0.504、0.576 cm/s，枝晶生長速度隨著無量綱過冷度的增加而明顯增加.無量綱過冷度對冰晶凝結的主要影響在于，無量綱過冷度越大，界面厚度就越薄，凝固時散發的潛熱就越多，從而使冰晶凝固速度更快.因此，代入實際物理量后可知，過冷度越低，冰晶凝固越快，且凝固速度與過冷度基本為線性關系.

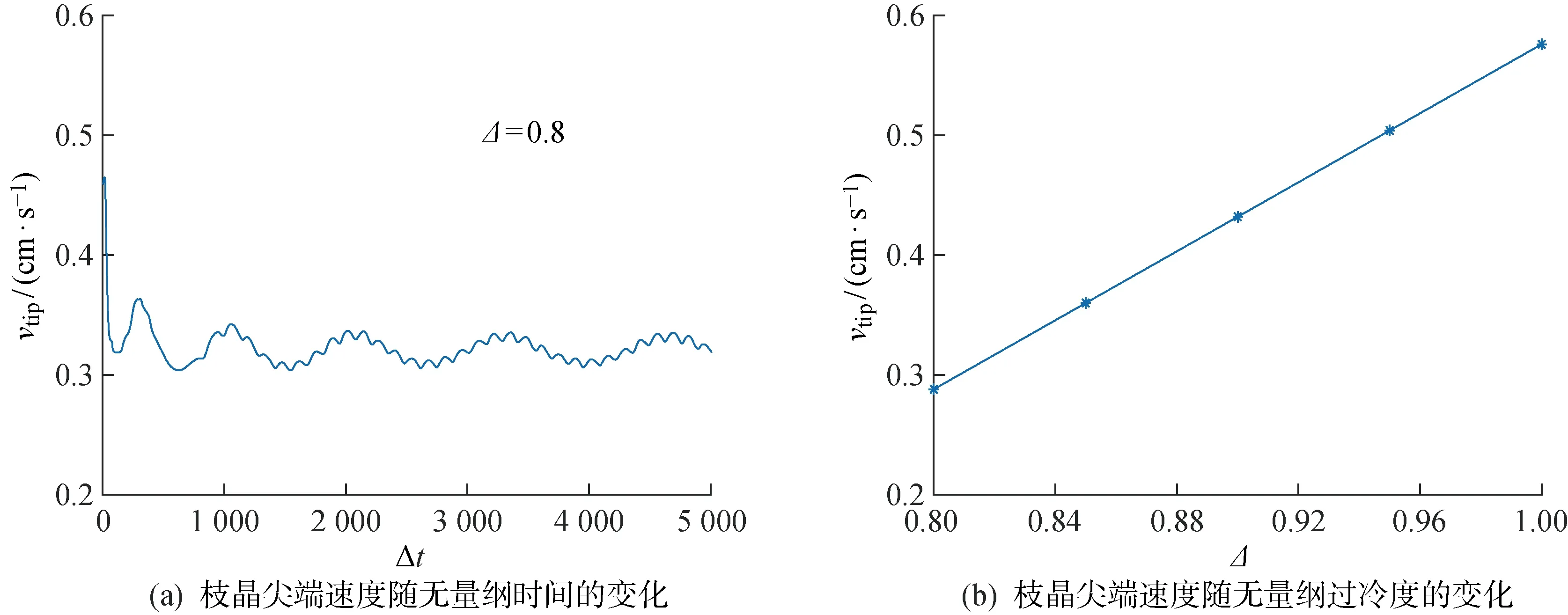
圖5 枝晶尖端速度變化情況Fig.5 Changes of dendrite tip velocity

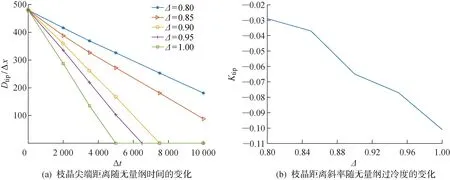
圖6 枝晶尖端距離及枝晶距離斜率變化Fig.6 Changes of dendrite tip distance and dendrite distance slope

3.3 過冷度對多晶核生長形狀的影響

本文在計算域內設置4個晶核，在晶核初始間距相同的情況下，通過計算不同過冷度下各晶核主枝之間的距離變化來分析過冷度對海水結冰的影響情況.

不同過冷度下枝晶尖端距離Dtip隨無量綱時間的變化如圖6(a)所示.隨著無量綱時間的增加，枝晶尖端間距逐漸減小，且二者呈線性關系.當無量綱過冷度達到0.90時，枝晶間距最終為0，代表不同晶核生長出的枝晶最終接觸.根據圖中趨勢，無量綱過冷度越大，接觸所需時間越短.圖6(b)為將枝晶尖端距離隨時間變化的曲線擬合為一次函數后的曲線斜率Ktip，其代表枝晶間距的變化快慢，即枝晶生長速度的大小.根據曲線所示，斜率與無量綱過冷度之間近似呈線性關系，說明了隨著無量綱過冷度的增大，枝晶生長速度的變化也會相應地近似呈線性增大.

4 結論

基于Wheeler相場模型，使用有限差分法，將海水看作鹽-水二元溶液，把實際物理量轉換為方程中的無量綱數，提取出枝晶生長速度作為定量分析海水結冰的指標，并通過不同過冷度下各晶核枝晶之間的間距變化來描述過冷度對海水結冰的影響.具體結論如下：

(1) 無量綱過冷度為0.90以下時，枝晶較細，沒有或僅有二級分枝，枝晶生長較慢.無量綱過冷度為0.90和0.95時，枝晶較粗，枝晶生長速度較快，出現二級以上分枝.無量綱過冷度為1.00時，主枝與分枝明顯變粗，生長速度明顯加快，分枝之間幾乎無空隙.

(2) 無量綱過冷度為0.80時，枝晶生長慢，形狀細，晶核內部空隙大，最終形成各主枝組合成的枝狀冰晶.無量綱過冷度為0.90和0.95時，有多次分枝，分枝之間有一定空隙，且空隙隨著分枝發展而減少.無量綱過冷度1.00時，枝晶生長速度快，分枝之間空隙小，晶核內部空隙被填滿，形成冰盤.

(3) 在各過冷度下，枝晶生長速度較為穩定，尖端最大速度隨無量綱時間呈正弦變化.無量綱過冷度從0.80增至1.00時，枝晶尖端生長速度從0.12 cm/s增至0.24 cm/s，生長速度與過冷度之間為線性關系.

(4) 枝晶尖端間距隨著時間的增加而減小，且二者呈線性關系，間距曲線斜率與無量綱過冷度之間近似為線性關系，其反映了枝晶生長速度的與無量綱過冷度之間也近似為線性關系，與之前求得的枝晶尖端速度相吻合.