連續液相碎化過程數值模擬研究

＊蘭治科 李勇 蘇光輝 昝元鋒

（1.中國核動力研究設計院 四川 610041 2.西安交通大學核科學與技術學院 陜西 710049）

液體霧化過程包含了能量和質量轉化、連續液體顆粒化等物理過程，在現代社會被廣泛應用各個領域，如農業噴霧、噴涂、發動機、航空航天、核能等。根據用途不同，對霧化性能的要求也不盡相同。因此獲得特定噴霧頭的相關性能參數顯得尤為重要，特別是霧化后的液滴粒徑、流量密度分布和霧化錐角。

由于噴霧機理的復雜性，到目前為止還沒有能夠完整、準確描述噴霧頭性能的好方法。目前的研究方法主要有三種，分別為實驗研究、理論計算和計算流體力學（CFD）模擬。其中理論計算主要是建立在半經驗公式的基礎上，而關于實驗研究，高昂的實驗成本以及測量精度，仍是主要的制約因素。特別是應用于某些特殊領域的大型噴霧頭，如穩壓器、安全殼中的噴霧設備，其共同特點是：噴霧頭尺寸和噴霧流量大，液滴粒徑分布范圍較廣，普通粒徑測量儀器不適用于該類型噴霧頭測量。此外，對于噴霧頭內部流場以及出口處液膜破碎過程等微觀現象研究，目前尚未找到適合的實驗方法。

隨著計算機性能提高，CFD被廣泛應用于霧化性能各項參數研究。采用數值模擬方法研究霧化現象有助于更加深入認識霧化機理和指導相關實驗，同時可以彌補噴霧實驗不足，提供噴霧實驗無法得到的流場分析結果。

然而，對于液體霧化數值模擬，CFD技術仍然面臨著較大挑戰。主要是因為霧化過程不僅牽涉到從單相液體到氣液共存兩相流動的過渡，同時，對于液相來說，還存在從連續相的液體到離散相液滴的轉變。目前幾乎所有的霧化場模擬均使用Eulerain-Lagrangian兩相流模型[1]。這種模型通常假定噴口附近的液滴粒徑和速度分布作為已知的邊界條件已經被確定，而獲得這些邊界條件的方法又往往依賴實驗或者經驗。因此，從嚴格意義上說，這種數值方法并不能實現噴霧過程的真正模擬。而Eulerain-Eulerain方法，相對于網格尺寸而言，僅局限于對兩種連續相共存的流場進行計算，并不能獲得完全離散化的液滴[2]。

基于以上原因，本文根據最大不穩定波增長率液膜破碎理論，在連續液相出口位置構建初級破碎模型-PBM，與噴霧頭內部流場和霧化場的數值模擬進行耦合，提出了一種全流場的數值模擬方法，實現從噴霧頭入口到霧化場的全過程數值模擬。最后，通過已有的實驗數據對以上方法進行了驗證，計算結果符合較好，證明了全流場數值模擬方法的有效性。

1.全流場模型構建

目前，在已有的兩相流模擬中，Eulerain-Eulerain法將兩相視為能夠互相穿插，但不相溶的連續介質。該方法使用空間和時間上為連續函數的相體積分數來模擬兩相在空間的分布。從噴霧頭入口全液相流動到出口連續液膜與氣相并存，符合Eulerain-Eulerain方法兩相模擬的要求。

Eulerain-Lagrangian方法用于噴霧場模擬，將噴霧空間的氣體介質作為連續介質，為其建立Eulerain坐標系；而將液滴顆粒當作離散介質，為其建立Lagrangian坐標系。該方法假定液相以離散液滴的形式進入連續氣相中，通過質量交換、能量交換和動量交換進行兩個相間的耦合。因此Eulerain-Lagrangian方法僅用于噴霧頭出口連續液膜破碎后的兩相流場模擬。

本文使用Eulerain-Eulerain法中VOF模型捕捉兩相之間界面，模擬從單相液體進入噴霧頭，直到出口位置形成液膜的內部流場；使用Eulerain-Lagrangian方法中DPM模型模擬離散液滴在氣相中的碰撞、破碎以及再分布過程。本文采用最大表面擾動波增長率破碎理論，構建了適合于大型噴霧頭的初級破碎模型（PBM）。通過在FLUENT求解器上使用UDF，編譯相關程序與以上兩個模型耦合，形成VOF+PBM+DPM的完整流場的數值模擬方法，模型結構見圖1所示。

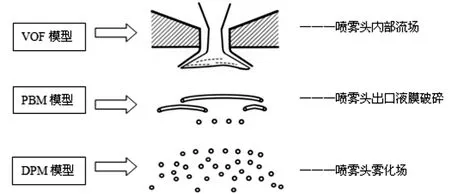
圖1 連續液相碎化過程數值模擬模型結構圖

2.全流場數值模擬過程及結果分析

(1)噴霧頭內部流場數值模擬

VOF方法是在1981年由Hirt和Nichols[3]首先提出，它使用一個標量場函數γ體積份數來表征第二相流體在計算網格中的分布，其大小為第二相流體在網格中所占體積百分比。因此，VOF又被稱為流體體積法。在本文霧化模擬中，環境介質空氣作為第一相流體，霧化介質水作為第二相流體，所以體積分數γ代表網格控制體中霧化介質水的體積份額。

根據體積分數的標量場γ，全計算域流體物性密度ρ以及粘性μ的表達式如下：

其中ρ1、ρg分別為液相和氣相所對應的密度；μ1、μg分別為液相和氣相所對應的粘性應力。因此，在液相、氣相以及兩相混合區域均使用式（2）中流體物性，可以使在流體力學相關控制方程中按單流體模型僅使用一套方程組。

體積分數函數γ滿足如下輸運方程：

噴霧頭內部結構和流道對霧化特性起決定作用，因此在計算過程中需要對網格質量進行獨立性驗證。本文定義了4種不同的網格方案，對網格逐漸加密對流量特性及霧化錐角的影響進行了比較。當網格精度進一步提高，以上特性參數不再明顯變化時即認為網格質量滿足獨立性條件。

本文為螺旋槽式旋流噴頭提供連續液相入口，在大多數情況下均表現為強烈的旋流特征，為了避免標準κ-ε模型的缺陷，湍流模型考慮κ-ε模型的修正方案：RNGκ-ε模型。FLUENT求解器三維旋流計算中通過旋流因子as對RNG κ-ε模型中的μt進行修正。計算前對as=0.070，0.075和0.080三種不同旋流因子時流動特性計算值與實驗值進行了比較，認為as=0.080作為湍流模型旋流因子比較適合該類型噴霧頭的旋流強度。

連續液相破碎數值模擬，使用VOF模型從噴霧頭入口為時間和迭代開始起始點。圖2為噴霧頭內部流場瞬態圖。噴霧頭在流動擾動過程中，在噴霧頭混合腔接近出口位置出現較為明顯的旋流、直流分層流動。其中直流部分位于正中心豎直向下，而旋流則沿四周壁面繞流。而在旋流作用下，混合腔內部易形成負壓區，容易發生大氣壓力下環境介質中空氣倒流現象。而直流與旋流交界處則成為相對較為“脆弱”的位置。

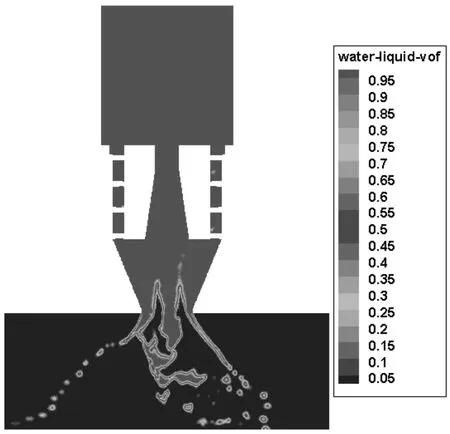
圖2 連續液相碎化為液帶過程圖

(2)噴霧頭出口初級破碎模擬

在噴霧頭出口建立液膜射流的幾何模型，假定液膜以錐形射進入環境空氣。液膜與空氣相互作用，在液膜表面上形成擾動波。

通常認為，擾動波滿足如下關系式：

假設擾動波是導致液膜破碎[4]的主要原因，當擾動波增長率達到最大值時，液膜發生破裂，形成初始液滴。通過色散方程對式（4）進行求解，最終得到最大增長率對應下液膜破碎破碎模型PBM。

使用UDF中的DEFINE_EXECUTE_AT_END宏，在瞬態計算的每個時間步長統計噴霧頭孔口所在面每個網格單元的流動信息。通過采集兩相VOF模型在噴霧出口的計算結果作為邊界條件輸入霧化初級破碎模型。對旋流噴霧頭，假定孔口液膜以環狀形式存在，通過液相截面積相等的方法獲得PBM初始液膜厚度。

通過PBM模型獲得破碎距離后，在FLUENT求解器中通過UDF功能統計某一時間段內在該距離橫截面上瞬態流量分布，獲得該截面上霧化場流量密度分布。UDF由編輯宏DEFINE_EXECUTE_AT_END程序以及定義F_UDMI存儲瞬態數據完成，在橫截面每個face類型的網格單元中累積該時間步下經過該網格的質量流量，最終得到某一時間段內截面上的流量分布如圖3所示。

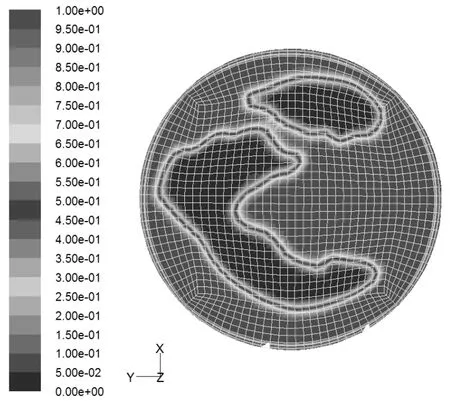
圖3 液膜破碎截面流量密度分布

(3)噴霧場數值模擬

在DPM模型中，通過積分拉式坐標下的顆粒作用力微分方程來求解離散相顆粒的軌道。顆粒運動方程：

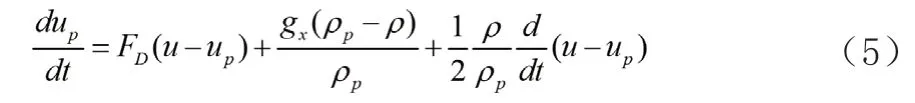
其中u、up分別為流體和顆粒的速度；ρ、ρp分別為流體和顆粒的密度；FD(u-up)為顆粒的單位質量曳力。此外，液滴碰撞模型基于O'Rourke理論；液滴破碎模型適用TAB模型。

為了降低計算成本，本文構建2-D幾何模型對噴霧場豎直截面內離散液滴流動特性進行數值模擬。該幾何模型在原有VOF模型的正下方，選取過噴霧頭軸心的豎直截面作為計算區域，其大小為4000mm×2200mm。

通過DPM模型可得到噴霧場溫度、速度等各項參數分布。圖4為霧化場液滴粒徑分布計算結果。從圖中可以看出，噴霧場中較大粒徑液滴主要位于霧化場外側。原因在于噴霧頭霧化過程以旋流特征為主，即大部分霧化液體以旋流方式沿霧化錐角外側方向進入噴霧場。其次，霧化場粒徑分布圖中左半側液滴粒徑均值明顯大于右半側，且顆粒分布較密。主要是因為在離散相邊界條件上，噴霧頭霧化液體并非對稱分布，大部分液體分布在邊界條件的左側區域。

圖4 噴霧場液滴粒徑分布

3.全流場數值模擬與實驗結果對比

針對本文研究對象，在數值模擬工況下開展了相應實驗研究，具體實驗研究內容和方法詳見文獻[5]，此處不再贅述。

圖5給出了通過全流場數值模擬方法計算得到的噴霧場液滴粒徑概率密度與實驗數據的比較。圖中橫坐標為液滴粒徑尺寸，曲線為計算得到粒徑分布，離散點為實驗測試得到的實際粒徑概率分布，兩者分布趨勢符合較好，表明了全流場數值模擬的有效性。

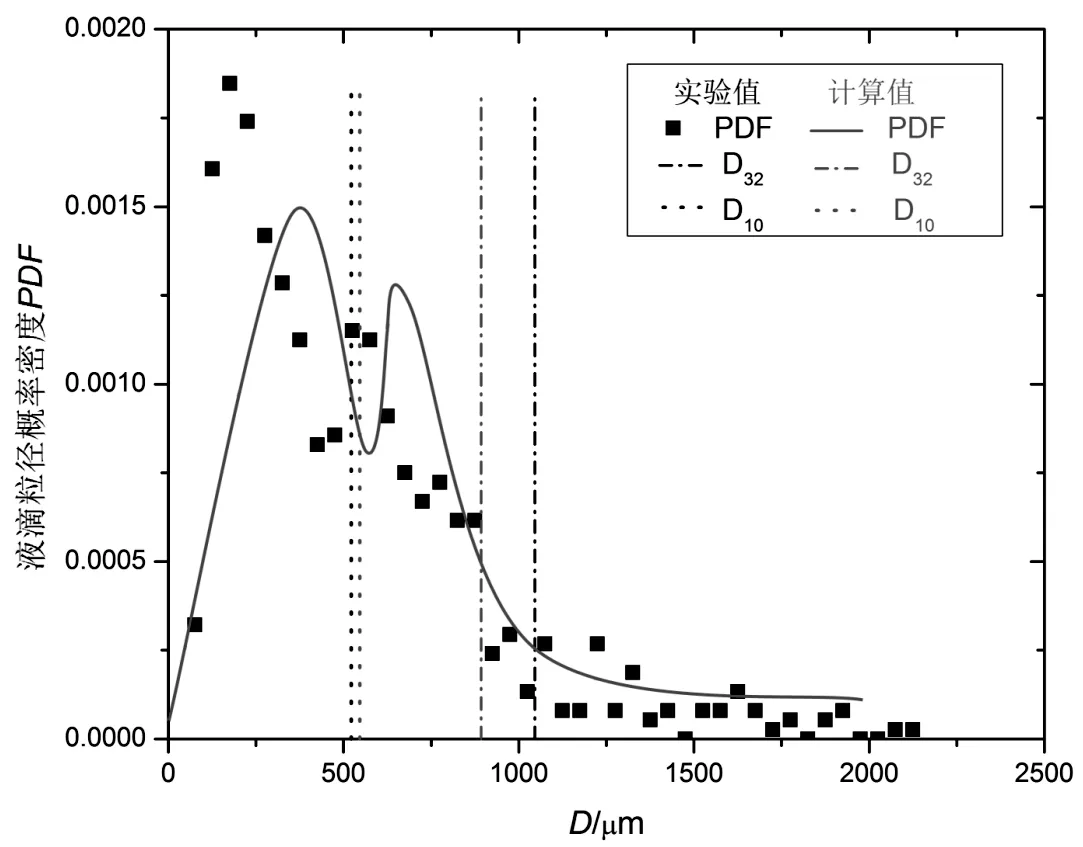
圖5 液滴粒徑概率密度計算值與實驗數據比較

4.結論

本文針對連續液相，提出一種全流場液相破碎數值模擬方法。通過構建初級破碎模型PBM，與用于內部流場計算的VOF模型和霧化場計算的DPM模型進行耦合，實現了從連續液相到霧化顆粒的噴霧全過程數值模擬。最后與實驗結果對比，證明了VOF+PBM+DPM全流場模型的有效性。解決了目前霧化數值模擬中，Eulerain-Eulerain和Eulerain-Lagrangian方法僅能模擬局部過程的問題，為連續液相破碎及霧化場研究提供了一套完善的數值計算方法。