基于屬性拓撲的螺桿轉子型線分析

（陜西理工大學機械工程學院,陜西漢中 723001）

1 引言

螺桿壓縮機的運轉部件少、大修期長、工作時可以強制輸氣、動平衡性好[1]，可應用在粉塵、煤礦和工藝氣體等車間內，也可裝備在尺寸和工作條件嚴苛的機車、船舶等設備上。

螺桿轉子作為螺桿壓縮機的主要零部件，要求齒面精度高、齒間流量大、泄漏量小等，由于第一代對稱型線很難滿足工作要求，這種設備在當時并沒有得到普及。20世紀70年代，通過對原始不對稱型線的改進，第二代不對稱的轉子型線降低了內部泄漏，提高了熱力學效率，同時隨著精密螺紋銑床的發展[2]，不僅保證轉子復雜型面的精度，其生產成本也大大降低[3]。轉子型線發展至今，新一代型線在優化的同時引入了橢圓、橢圓包絡線等新曲線類型，接觸線更短，內部泄漏降低約90%[4]，工作性能得到了進一步提升。

傳統的型線設計方法是從二維曲線出發，先設計陰陽轉子中的一個型線，再利用嚙合原理生成一對端面曲線和空間曲面[4-6]；后來，出現了通過多變量全局優化改進某種型線既而生成新型線的方法[7]；近些年，以滿足技術指標的嚙合線為前提，通過調整影響工作性能的參數[8]或調整三次樣條曲線控制點[9]來逆向解析生成新型線的方法被廣泛采用。

但是，這類利用高次樣條曲線生成型線的方法，不僅和先進齒形有很大差距，而且仍需要包絡線上的離散點組才可以加工[10]。與此同時，這類型線對生產轉子的刀具、工裝和機床等要求也會相應提高，理論上最佳性能的轉子未必能夠大批量生產。因此，仍需回歸到經典的轉子型線中，用定量的數學方法進行計算，尋找出通用性強且性能優異的嚙合對，為下一步設計工作奠定基礎。

屬性拓撲是圖論與形式概念分析的結合[11]，分別用對象和屬性代表形式概念中的外延和內涵，并給屬性關系賦權值，直觀的展現形式背景中屬性間的各類拓撲關系[12]。目前，屬性拓撲已應用在數據分析[13]和醫療診斷[14]等方面。本文首次將屬性拓撲理論引入轉子型線分析過程，對歷經時間檢驗的轉子型線嚙合對進行形式概念計算，利用該數學語言精確地分析不同的曲線類型與螺桿壓縮機性能的關系，為生成新型線提供思路。

2 螺桿轉子型線的屬性拓撲生成

2.1 螺桿壓縮機轉子型線

螺桿壓縮機的氣缸通常呈“∞”形，在缸內平行配置按一定傳動比反向旋轉的一對相互嚙合的螺旋形轉子[1]。凸齒的是陽轉子，凹齒的是陰轉子。從單個封閉腔體的工作特性來看，螺桿壓縮機可以視為多缸活塞式壓縮機；從垂直于軸線的橫截面來看，螺桿壓縮機的陰轉子由少齒數的斜齒輪發展而來、陽轉子由多頭數的蝸桿發展而來。鑒于形式概念計算的二值背景[15]，從端面型線的角度對螺桿轉子型線進行分析。

由于第一代型線的轉子并未被廣泛應用于工程實際，所以本文僅研究第二、三代轉子型線的曲線類型。圖1～4和圖5～8分別是4種第二代和4種第三代具有代表性的轉子型線，表1～8是對應的轉子型線組成齒曲線。

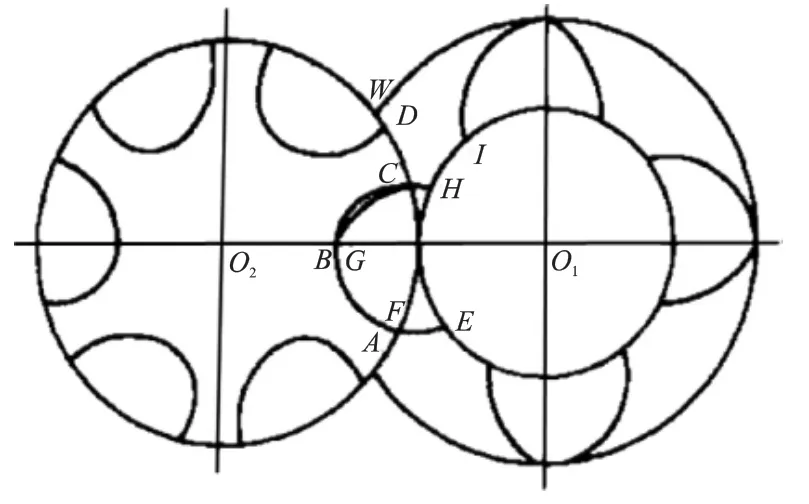
圖1 原始不對稱型線

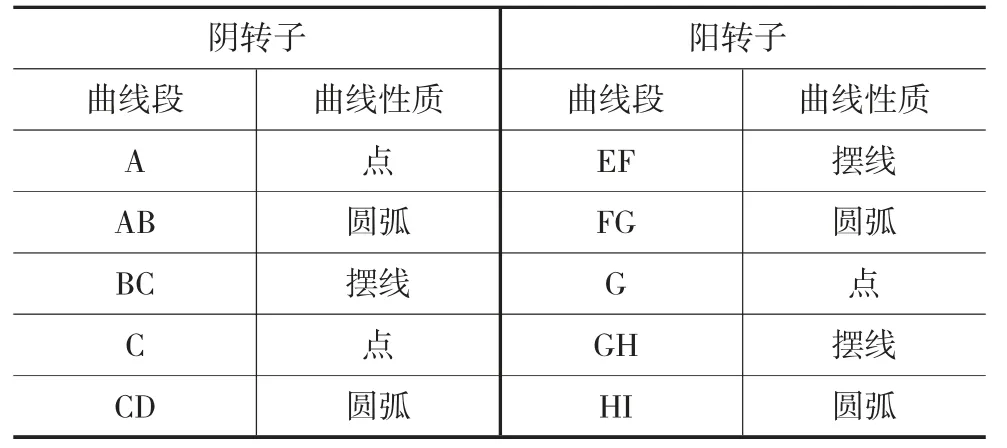
表1 原始不對稱型線組成齒曲線

2.2 轉子型線的屬性拓撲

屬性拓撲來源于形式概念分析，形式概念分析是應用數學的一個分支，而形式背景是形式概念分析的基本表示方法，根據計算需要引入下列定義與公式[11-12]。

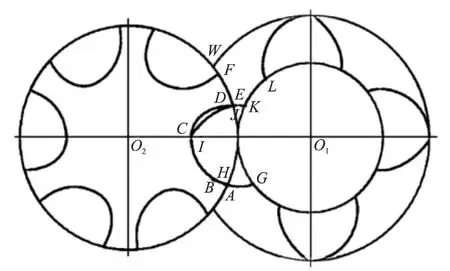
圖2 單邊不對稱-銷齒圓弧型線

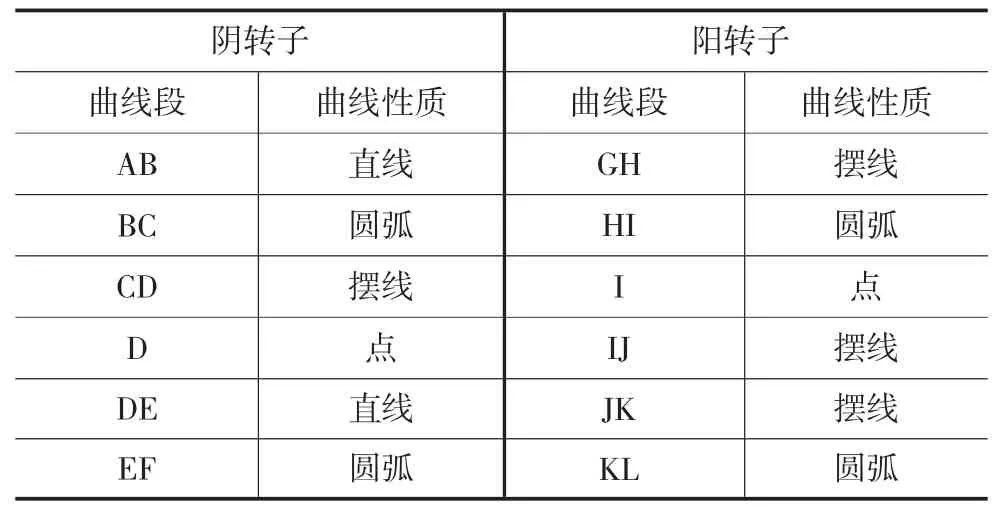
表2 單邊不對稱-銷齒圓弧型線組成齒曲線

圖3 Atlas-X型線

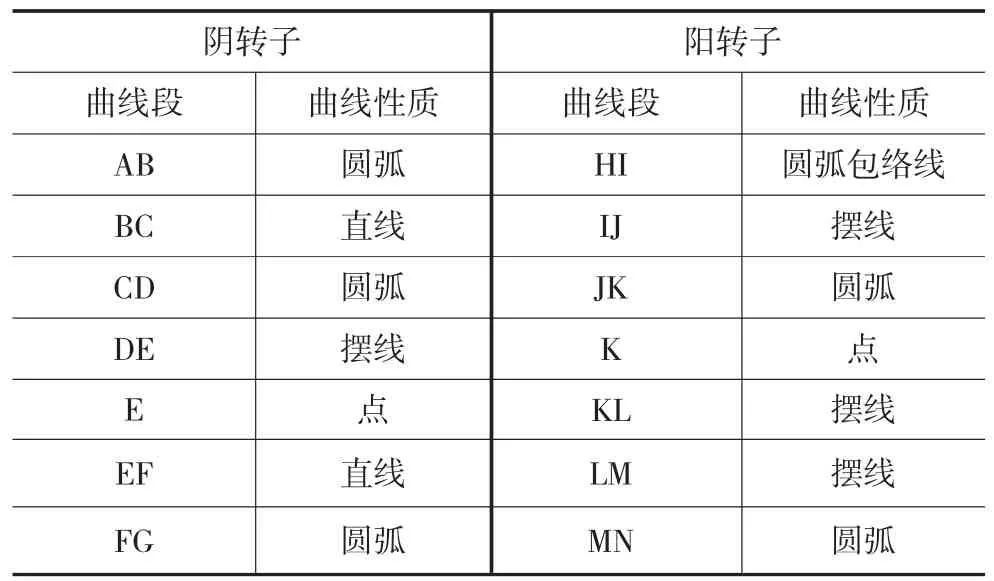
表3 Atlas-X型線組成齒曲線

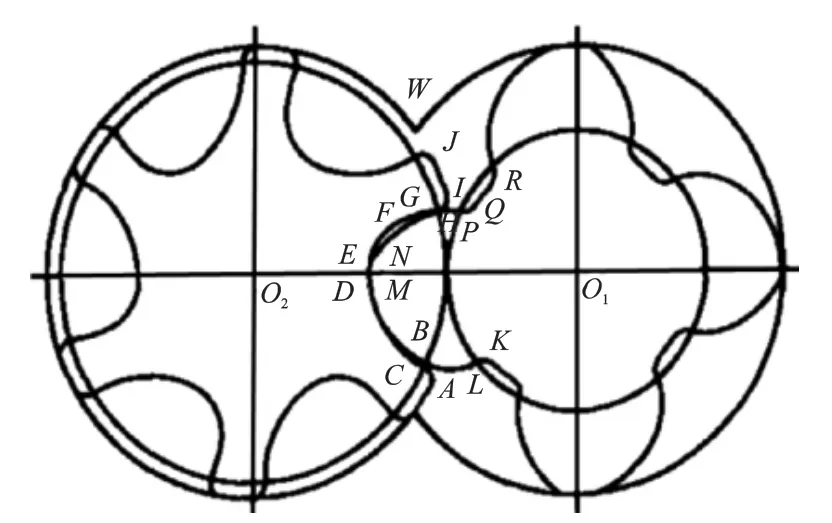
圖4 SRM-A型線

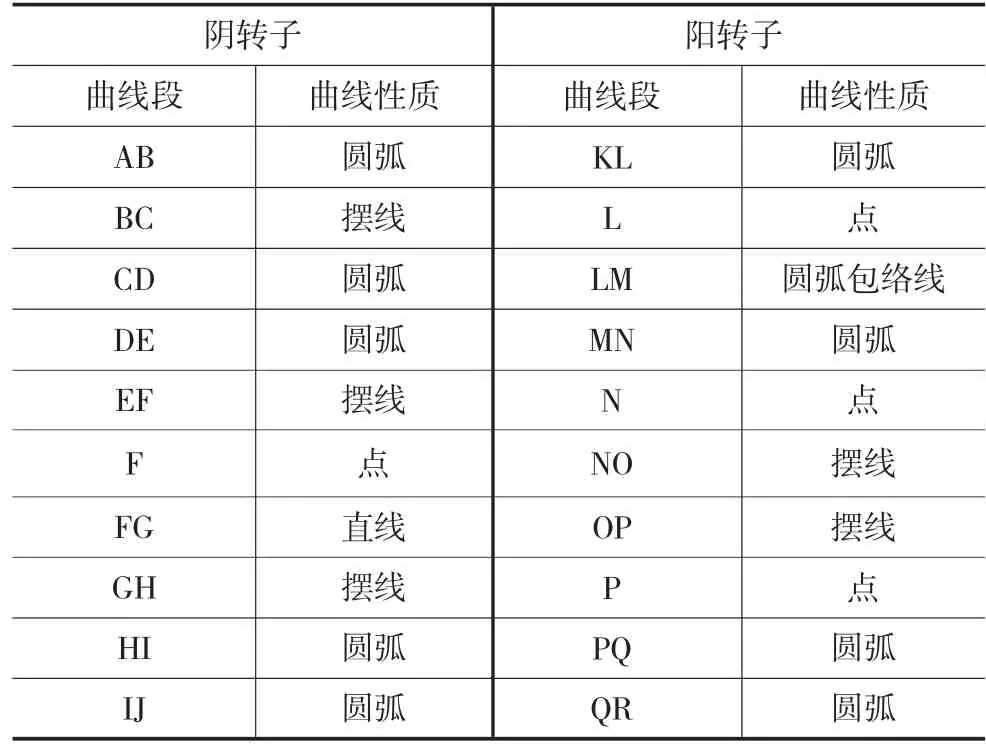
表4 SRM-A型線組成齒曲線

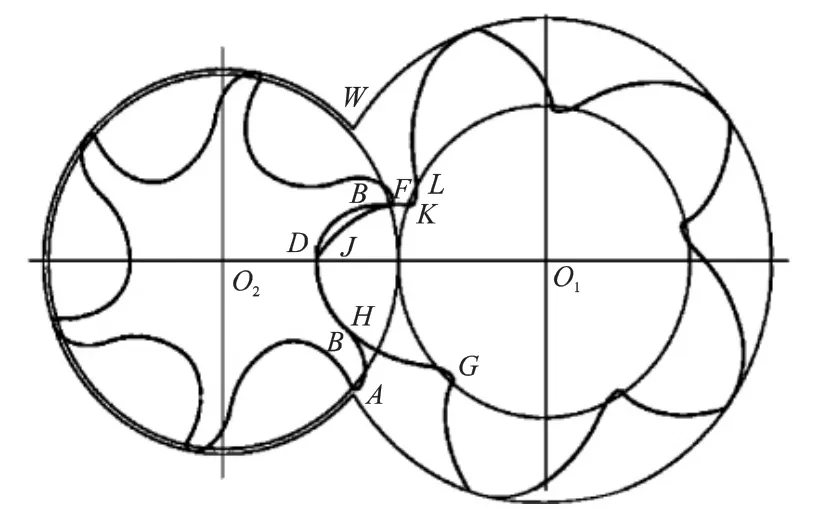
圖5 GHH型線

表5 GHH型線組成齒曲線

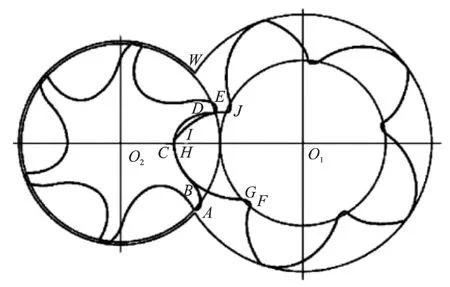
圖6 復盛型線

表6 復盛型線組成齒曲線

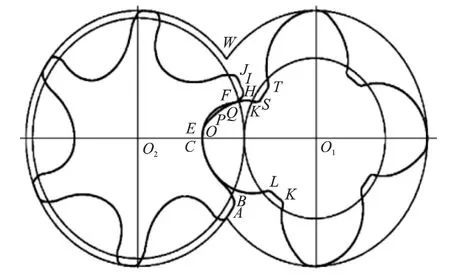
圖7 SRM-D型線

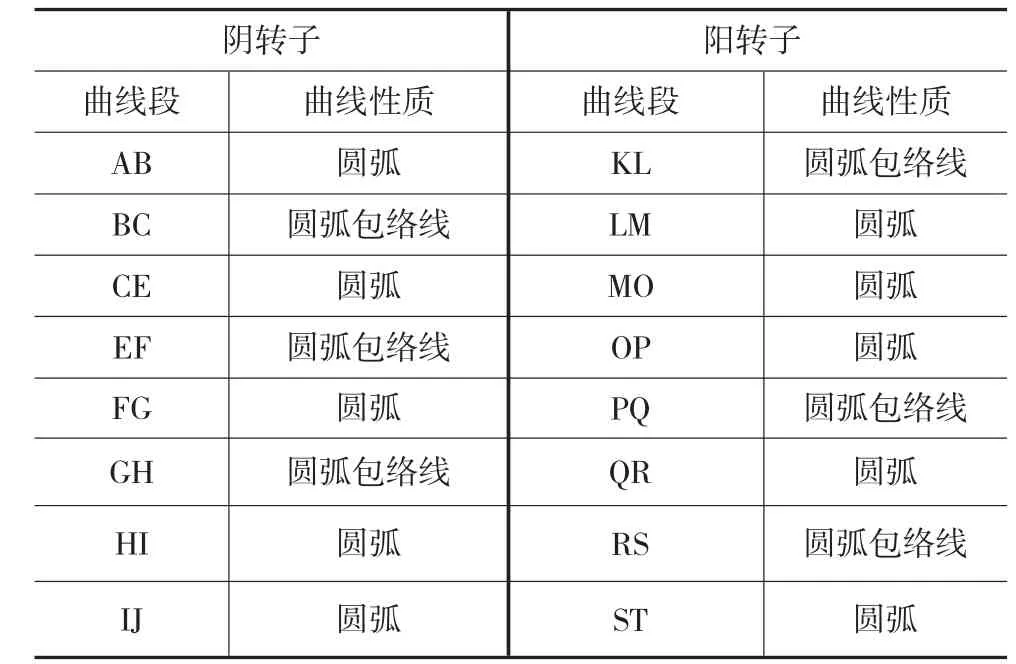
表7 SRM-D型線組成齒曲線

圖8 日立型線

表8 日立型線組成齒曲線

定義1 形式背景用三元組K=（G，M，I）表示，其中G表示所有對象的集合，M表示所有屬性的集合，I?G×M表示對象與屬性之間的關系，G×M表示集合G和集合M的笛卡爾積。若A?G，B?M，令

f（A）={m∈M|?g∈A，（g，m）∈I}

g（B）={g∈G?m∈B，（g，m）∈I}

如果A，B滿足f（A）=B，g（B）=A，則稱二元組（A，B）是一個形式概念，A是形式概念（A，B）的外延，B是形式概念（A，B）的內涵。

定義2 對于一個形式背景K=（G，M，I），M={m1，m2，…，mn}，屬性拓撲的鄰接矩陣表示法定義為T1=（V，E），V=M為屬性拓撲頂點集合，E為該屬性拓撲的鄰接矩陣，矩陣中每個元素代表從屬性mi到屬性mj邊上的權值。

定義3 屬性拓撲中的關聯矩陣表示法定義為T2=（V，E′），這種表示法只描述屬性之間的關系。其中E′為關聯矩陣

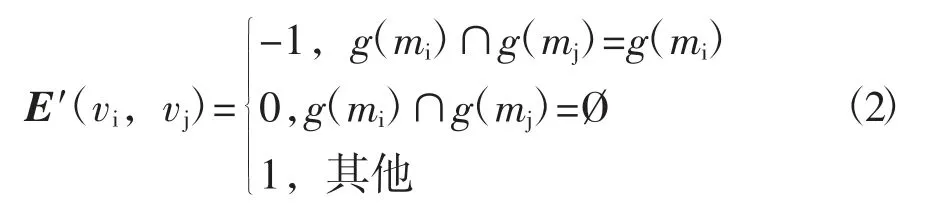
因為螺桿壓縮機需要兩轉子嚙合運轉，所以不單純分析曲線類型，將各嚙合對作為一個屬性進行分析。螺桿轉子型線嚙合對的形式背景如表9所示，表9中各符號含義見表10。

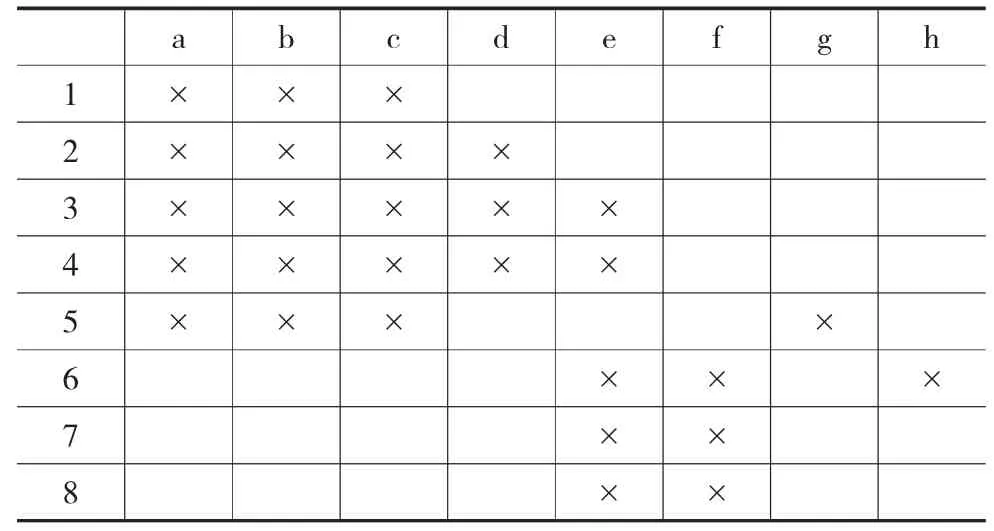
表9 螺桿轉子型線的形式背景

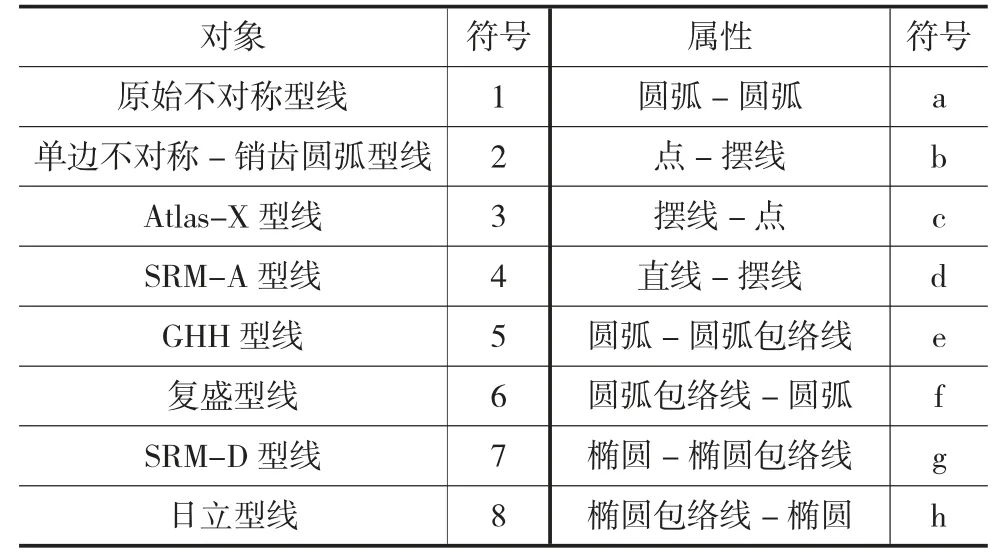
表10 符號表

形式背景中通常存在冗余信息，為進行簡潔地表達及運算，需要對形式背景進行預處理[11]。

最早采用包絡線的是SRM-A齒形，該齒形接觸線更短、密封效果更好，Atlas-X是從SRM齒形發展而來的，與作為國標的單邊不對稱銷齒-圓弧齒形區別不大，且沒有保護角不利于儲存運輸，直線段較長泄漏三角形較大[5]，故第二代型線中約去Atlas-X型線。SRM-D通過計算機優化設計得到，是一種可應用于各種場合的非特殊齒形[16]，日立型線是對SRM-D和GHH優點的綜合，故第三代型線中約去日立型線。嚙合屬性a、b和c的對象集相同，計算時合并為一個。經預處理后的形式背景見表11。

由式（1）和式（2）可得對應的鄰接矩陣E（vi，vj）和關聯矩陣E′（vi，vj）。然后按照關聯矩陣畫出各屬性間的關系。

轉子型線的屬性集合作為拓撲的頂點集合，按照關聯矩陣畫出屬性拓撲圖（圖9），并給各邊賦予權值。

由文獻[12]中關于不同屬性的定義可知，頂層屬性集（superordinate attributes，SPAs）為{c，e}，伴生屬性集（subordinate attributes，SBAs）為{d，g，h，f}，其中，{h}為多重伴生屬性。為進一步可視化計算，先將屬性拓撲進行有序化處理[11]，SPAsT={c，e}，（SBAsT）^={g，d，f，h}。全局屬性和空對象定義為起點屬性和起點對象，空屬性和全局對象定義為終點屬性和終點對象。M（SPAs,SBAs）={Ψ，SPAsT，（SBAsT）^，E}={Ψ，c，e，g，d，f，h，E}，如圖10。

表11 經預處理后的轉子型線形式背景

3 轉子型線屬性的異同分析

3.1 轉子型線的共性分析

通過屬性拓撲圖可以看出各屬性之間的不同關系及關聯強度，但是在工程實際中，通常希望找出性能優異且制造方便的型線類型，這類型線具有普遍適用性。屬性偏序圖可以將各類屬性在可視化的基礎上達到“物以類聚”的目的。通過文獻[11]的算法，先將螺桿轉子型線的屬性拓撲圖轉化為屬性偏序圖，具體過程見表12。

由最終的屬性偏序概念圖可以得出，“擺線-點”嚙合對的應用最為廣泛，說明其具有性能較好、應用范圍廣且加工難度低等特點；“圓弧和圓弧包絡線”嚙合對得益于其制造方便，應用的工作場合僅次于“擺線-點”嚙合對；“橢圓-橢圓包絡線”和“橢圓包絡線-橢圓”是第三代型線中新發展的類型，在特殊場合、大批量生產的改進型號中或不將成本作為首要考慮因素的設備上才有所應用。

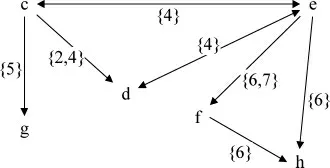
圖9 轉子型線的屬性拓撲

圖10 有序化處理后的轉子型線屬性拓撲

3.2 轉子型線的差異分析

在某些情況下，需要研究的不是通用性而是特性。將已生成的轉子型線屬性拓撲轉化為差異屬性拓撲[19]分析各嚙合對之間的具體區別。

定義4 差異屬性拓撲的鄰接矩陣表示法定義為T3=（V，EDM），V=M為屬性拓撲頂點集合，EDM為該屬性拓撲的差異鄰接矩陣，#EDM（mi，mj）定義為差異屬性拓撲中屬性mi指向屬性mj的邊加權的元素數，num（mi，mj）={#EDM（mi，mj）+#EDM（mj，mi）}。

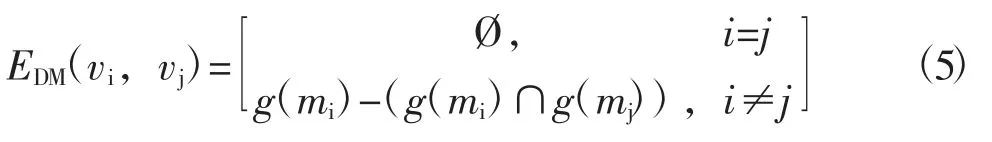
求出轉子型線的形式背景對應表13的差異鄰接矩陣，然后通過該矩陣畫出相應的差異屬性拓撲，見圖11。

差異屬性拓撲能反映屬性間的互斥關系[17]，而num（mi，mj）（表14）可以定量反映出屬性之間的差異程度。各屬性之間的差異程度計算之后列于上三角。

從表14可以得出，屬性c比屬性d、g的應用廣，屬性e比屬性f、h的應用廣，屬性f比屬性h的應用廣；屬性c與屬性f的差異是任兩屬性對之間差異最大的，說明第二代型線中常用的“擺線-點”嚙合對在第三代型線中的使用程度越來越低，原因可能是包括：機床精度的提升導致成本下降，用戶不再將成本作為交易需考慮的首要因素，以及圓弧類型線對的綜合表現明顯占優；屬性g到屬性c、屬性h到屬性e、f和屬性f到e的差異程度為0，導致num的值較低，說明第三代型線采用的生成方法和第二代型線差別不大，只是根據設計壓力比、工作條件的不同而導致最終型線樣式的不同。

表12 轉子型線屬性拓撲圖轉化為屬性偏序圖步驟

4 轉子型線屬性的因果分析，見表15

由于本文并非只分析某一代中的某一類典型型線，所以還需要分析不同性能、不同應用場合的轉子型線之間是否存在因果聯系。在已生成的轉子型線屬性拓撲的基礎上，通過文獻[18]的方法進行因果關系推斷。

圖11 轉子型線的差異屬性拓撲

表13 轉子型線的差異鄰接矩陣

定義5 在形式背景K=（G，M，I）中，若屬性mj是屬性mi的必要條件，即：g（mi）?g（mj），則稱屬性mj是屬性mi的部分因，屬性mi是屬性mj的果，記 作：mj→mi。若 存 在m1→mi，m2→mi，其 中i≠1，2，則稱屬性m1，m2共同為屬性mi的部分因，屬性mi為m1，m2的果，記作：（m1，m2）→mi。

為計算簡便，將屬性拓撲中邊的權值刪去，各屬性與其對象集作為一個頂點，簡化后的屬性拓撲見圖12，選擇屬性g作為初始屬性進行因果推斷，生成因果關系之后刪除的對象用空格代替以便觀察。

由最終結果可以得出，屬性e雖然是頂層屬性，但卻是屬性c、d的果，說明“圓弧-圓弧包絡線”嚙合對一開始并未出現，隨著計算機優化技術和加工技術的發展而興起；屬性c同時是屬性g、e和d的部分因，再次論證了“擺線-點”嚙合對的通用性很強；屬性g和屬性h不是任何屬性的部分因，說明“橢圓-橢圓包絡線”和“橢圓包絡線-橢圓”嚙合對是通過上一代嚙合對優化得到，截至目前應用范圍并不廣泛。屬性f、e、d既是因又是果，說明設計新一代型線除了優化原嚙合對之外，還將嚙合對作為一個元素，在兩轉子嚙合路徑上設計不同的排列組合方案，最后賦予不同的長度，而且每一個元素并非只使用一次。

表14 num（mi，mj）的值

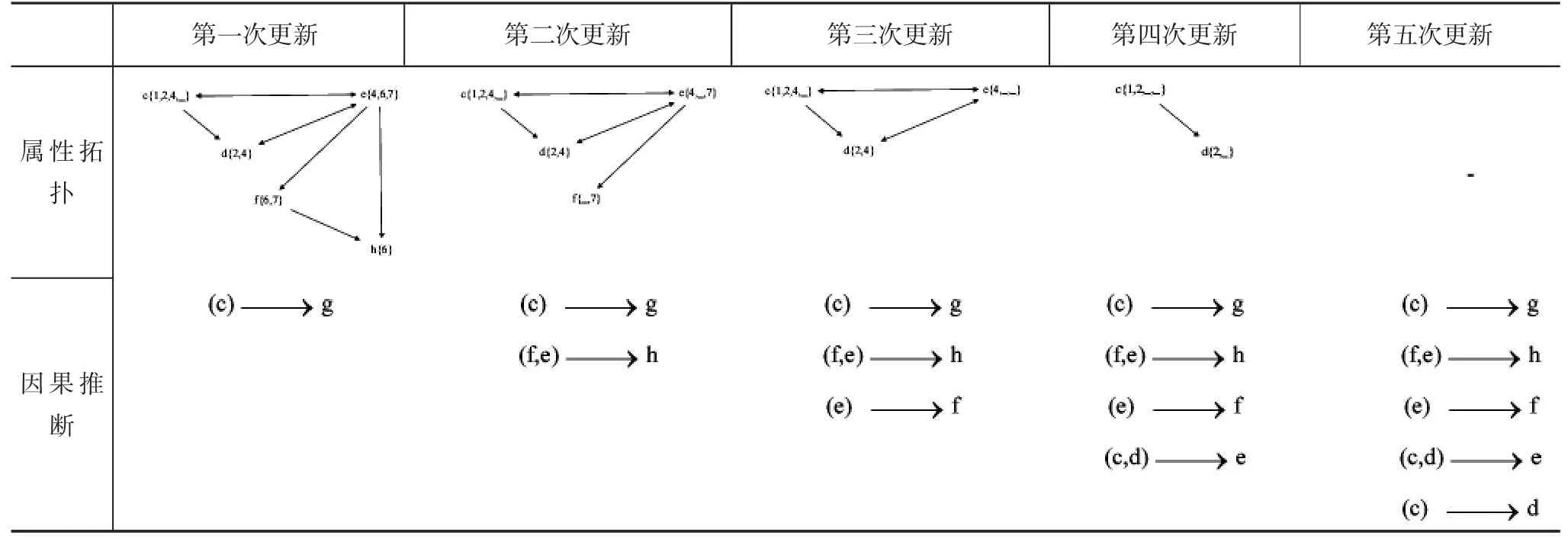
表15 轉子型線屬性的因果推斷

5 結論

轉子型線的好壞對螺桿壓縮機性能的影響非常大，在用戶要求不斷提高和市場競爭激烈的前提下，以經典轉子型線為基礎設計新型線的辦法具有很大優勢，這就需要先從經典型線中找出優異的嚙合對。首先，提取8種型線中的嚙合對，將其轉化為形式概念中的二值背景，然后生成屬性拓撲，再將其轉化為屬性偏序和差異屬性拓撲。分析出嚙合對的相同點：“擺線-點”嚙合對的通用性最強；“圓弧”類型的嚙合對隨著加工技術的提高和優化技術的發展而慢慢興起，至今在第三代中仍大量使用，說明該類嚙合對具有很高的工程價值。但隨著各企業的加工技術穩步提高，以“擺線-點”為代表的易加工但性能欠缺的嚙合對逐漸不受青睞，所以第三代型線已很少使用該嚙合對。

由差異度num值和因果關系可以分析出“橢圓-橢圓包絡線”和“橢圓包絡線-橢圓”嚙合對主要由“擺線-點”、“圓弧-圓弧包絡線”和“圓弧包絡線-圓弧”嚙合對發展而來，由于圓弧和橢圓對應的數學方程次冪相差不大，進一步得出如下結論：第三代型線以上一代型線為基礎進行優化，然后將優異的嚙合對作為一個元素，放入嚙入到嚙出的路徑上，設置不同的排列組合，需要注意的是每一種嚙合對并非只使用一次，最后賦予每段曲線不同的長度，從而達到提高性能、滿足客戶要求的目的。