基于小波去噪的灰色模型在變形監(jiān)測中的應用

武文銳，師思超

（1.山西華冶勘測工程技術有限公司，山西 太原 030000）

在變形監(jiān)測的過程中，由于觀測條件的影響，獲取的觀測值會出現(xiàn)誤差，從而給分析觀測數(shù)據(jù)和總結變形規(guī)律帶來一些干擾。信噪分離能大大提高預測模型的精度，因此將原始形變數(shù)據(jù)中的噪聲與真實值分離，并把相對真實的變形數(shù)據(jù)提取出來，是變形監(jiān)測數(shù)據(jù)預處理的重要目的[1]。對于變形監(jiān)測來說，觀測數(shù)據(jù)往往沒有較明顯的概率分布特征，且數(shù)據(jù)量不大；而時間序列、BP神經(jīng)網(wǎng)絡、回歸分析等方法均對樣本容量要求較高，且需要大量符合概率分布的訓練樣本，因此實際工程應用中上述數(shù)據(jù)處理方法受到了客觀條件的限制。基于小波分析的閾值去噪法對處理離散的變形觀測數(shù)據(jù)具有獨特的優(yōu)勢，能利用閾值函數(shù)從含噪數(shù)據(jù)中區(qū)分出噪聲和較為真實的變形數(shù)據(jù)。利用剔除噪聲后的數(shù)據(jù)進行變形預測分析可大大提高預測模型的精度[2]。因此，閾值法小波去噪在變形監(jiān)測中具有較強的工程實踐價值。

灰色模型的基本原理為對原始數(shù)據(jù)進行預處理，使數(shù)據(jù)能表現(xiàn)出指數(shù)函數(shù)的規(guī)律，再利用該指數(shù)函數(shù)進行變形預測[3]。灰色模型的建模方式簡單，最少只需4個數(shù)據(jù)即可建立模型，能在“貧數(shù)據(jù)”的情況下總結數(shù)據(jù)變化規(guī)律，在實際工程應用，特別是變形監(jiān)測應用中具有更強的實用性。雖然灰色模型短期預測的精度較高，但其長期預測能力卻不夠理想，這是由數(shù)據(jù)中的噪聲所導致的。因此，利用閾值法小波去噪盡可能地削弱觀測誤差的影響，減小隨機性，從而大大降低預測難度，提高預測精度。

1 閾值法小波去噪

1.1 小波去噪原理和方法

經(jīng)過小波分解后，小波域中真實信號與噪聲信號的表現(xiàn)形式差距較大，即隨著尺度的變化二者的幅值有差異。通常，隨著尺度的增加，噪聲幅度將不斷減小，而有效信號則不會發(fā)生變化[4]，小波去噪正是基于該原理來實現(xiàn)信噪分離的。

極大值法去噪、相關性法去噪、閾值法去噪等都是基于小波去噪理念實現(xiàn)的[5]，其中閾值法去噪因其簡單的計算方法和令人滿意的去噪效果被廣泛應用于工程實踐中。

含噪數(shù)據(jù)可表示為：

式中，f(t)為含有噪聲的觀測數(shù)據(jù)；s(t)為真實信號；n(t)為噪聲信號；噪聲信號的方差為σ2，服從N(0,σ2)。

觀測數(shù)據(jù)中包含真值與噪聲，真值是平穩(wěn)的低頻信號，噪聲是不平穩(wěn)的高頻信號。閾值法小波去噪的原理為通過設定一個閾值來收縮和保留大于該閾值的真實信號[6]，從而去除小于該閾值的噪聲信號，因此閾值法小波去噪也被稱為“小波收縮”[7]。

閾值法小波去噪分為3個步驟：①小波分解，確定小波的分解類型和層數(shù)，將原始信號分解成細節(jié)信號與近似信號之和；②閾值處理，設定一個閾值，利用閾值函數(shù)對高頻信號進行閾值處理，從而剔除噪聲；③小波重構，通過逆小波變換將低頻信號和經(jīng)過閾值處理后高頻信號重構為去噪后的信號[8]。

1.2 閾值函數(shù)和閾值選取

多年來，許多學者根據(jù)具體工程對改進閾值函數(shù)進行了各種嘗試，但基本分為硬閾值和軟閾值兩種。硬閾值是將絕對值小于閾值的小波系數(shù)置零[9]，保留其余信號，但該方法往往會使輸出信號發(fā)生震蕩；而軟閾值則是將絕對值小于閾值的小波系數(shù)減去閾值，而不是單純的置零，這樣會使輸出信號更加連續(xù)光滑。由于變形監(jiān)測點的形變在時空上是連續(xù)的，因此本文選取軟閾值函數(shù)作為去噪函數(shù)。硬閾值函數(shù)為：

軟閾值函數(shù)為：

式中，w為原始小波系數(shù)；為去噪后的小波系數(shù)；sign()為符號函數(shù)；λ為閾值M為信號長度。

在閾值處理過程中，不同的閾值選取方法對信噪分離效果將產(chǎn)生較大影響。常用的閾值選取方式為自適應閾值和默認閾值，其中自適應閾值包括固定閾值、極大極小閾值、啟發(fā)式閾值和無偏風險估計閾值4種。對于軟閾值函數(shù)來說，固定閾值的去噪效果更好。其計算公式為：

1.3 小波去噪精度指標

針對不同的小波函數(shù)和分解層數(shù)，小波去噪將有不同的去噪效果。去噪效果主要通過均方根誤差（RMSE）和信噪比（SNR）來衡量，RMSE越小、SNR越高，去噪效果越好[10]。

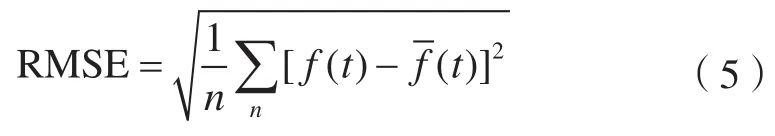
式中，f(t)為原始數(shù)據(jù)；為去噪后數(shù)據(jù)。

式中，powers為真實數(shù)據(jù)的功率；powern為噪聲的功率。

2 灰色模型

灰色模型的原理較簡單，但只能針對指數(shù)函數(shù)進行預測，因此需將原始數(shù)據(jù)進行一次累加，從而生成一個新的指數(shù)型序列。根據(jù)新數(shù)據(jù)能擬合得到一個指數(shù)函數(shù)，再根據(jù)這個函數(shù)可推算出下一個累加值，然后將累加預測值還原即可生成原始數(shù)據(jù)的預測值。原始序列為：

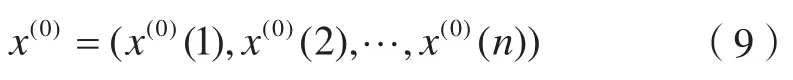
2.1 數(shù)據(jù)檢驗與預處理

灰色模型建模必須先檢驗原始數(shù)據(jù)是否能滿足建模條件。常用的方法包括檢驗指數(shù)規(guī)律、光滑性、級比檢驗等，本文選擇級比檢驗。級比檢驗的計算公式為：

雖然需采用新序列y(0)建模，但必須對最終結果進行還原，即將輸出序列同時減去常數(shù)c，還原成原始數(shù)據(jù)的模擬值。

2.2 建模方法

將原始序列累加得到：

計算x(1)的均值，則有：

建立灰色微分方程，即

則相應的白化微分方程為：

令u=[a,b]T，構造累加矩陣B和常數(shù)向量Y，則有：

利用最小二乘原理可確定達到最小值的參數(shù)列u的估測值為：

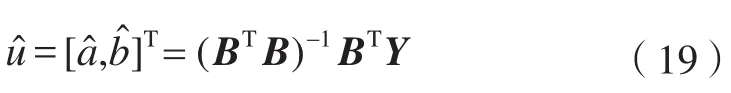
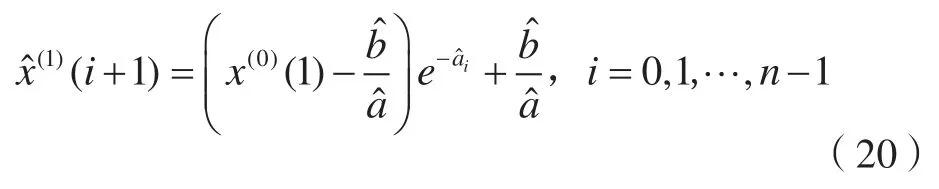
2.3 精度檢驗

灰色模型精度檢驗的常用方法包括關聯(lián)度檢驗法、殘差檢驗法和后驗差檢驗法[11]，本文采用后驗差檢驗法。通常利用小誤差概率p和后驗差比值C來共同衡量模型精度，p越大、C越小，則模型精度越高[3]。若p＞0.95、C＜0.35，則說明模型擬合精度極好。

令x(0)(k)為實際值，為預測值，殘差為e(k)，則有：

原始數(shù)據(jù)x(0)的方差為：

殘差序列e的方差為：

后驗差比值為：

小誤差概率為：

3 工程應用

本文對某高鐵隧道進行二等水準監(jiān)測，監(jiān)測周期為7 d，選取其中10期監(jiān)測點M的沉降數(shù)據(jù)作為樣本數(shù)據(jù)（表1）進行分析，對后5期數(shù)據(jù)進行預測。

表1 M點累計沉降原始數(shù)據(jù)

原始序列為：

首先計算原始數(shù)據(jù)的級比，發(fā)現(xiàn)不滿足建立灰色模型的條件，因此需進行數(shù)據(jù)預處理。通過計算發(fā)現(xiàn)，C=1時能滿足建模要求，則原始序列平移為：

3.1 灰色模型預測

按照上述灰色模型建模步驟建立模型，并預測后5期數(shù)據(jù)，結果如表2所示。

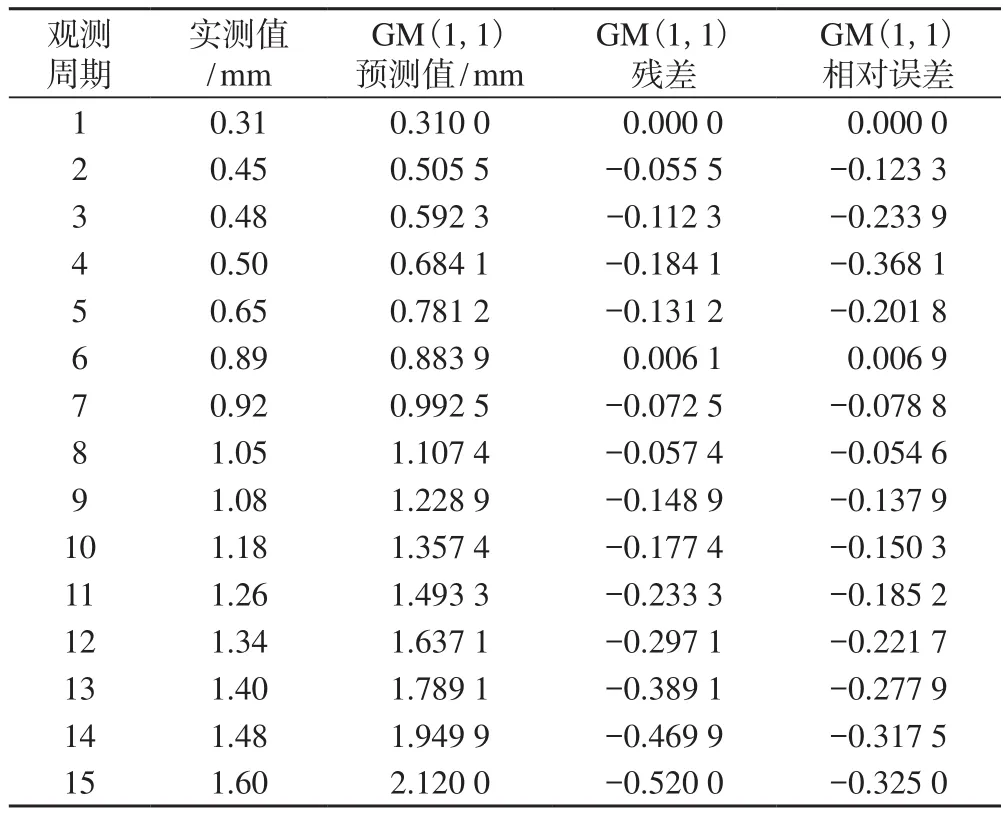
表2 M點灰色模型累計沉降預測分析

通過計算得到：p=1、C=0.220 7，說明模型的擬合精度較好。

3.2 閾值法小波去噪后的灰色預測

本文采用軟閾值法對原始數(shù)據(jù)進行去噪，小波函數(shù)選用db3、db4、db5小波，最大分解尺度為2和3，共計6種組合，分別計算并比較RMSE和SNR，從而選擇最優(yōu)函數(shù)組合進行小波分解，結果如表3所示。通過對比分析發(fā)現(xiàn)，當采用db4函數(shù)進行兩層分解時，SNR較高、RMSE較小，去噪效果更好，因此本文選用該分解方式進行信噪分離，結果如圖1所示。

表3 小波函數(shù)去噪評價分析

圖1 db4小波分解

利用軟閾值法剔除噪聲，再進行小波重構。去噪后噪聲殘差分析如圖2所示，可以看出，殘差在0附近波動，最大值為0.055 72，最小值為-0.000 4，標準差為0.030 75，說明信噪分離效果較好。小波重構后得到一組新的序列，即去噪后數(shù)據(jù)，如表4所示；再利用去噪后數(shù)據(jù)進行灰色模型建模，預測后5期數(shù)據(jù)，結果如表5所示。

圖2 噪聲殘差分析

表4 去噪后數(shù)據(jù)

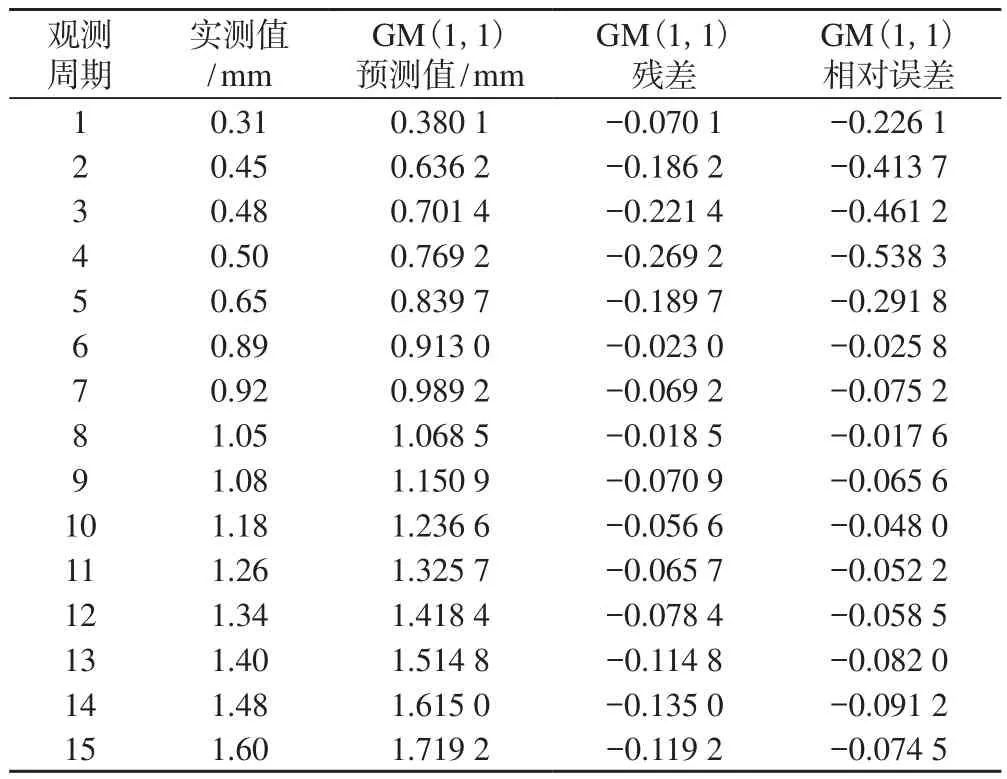
表5 去噪后灰色模型累計沉降預測分析

通過計算得到：p=1、C=0.214 1，說明模型的擬合精度較好。

3.3 分析比較

單純的灰色模型和小波去噪后的灰色模型的精度均很高，模型擬合度較好，二者都能對高鐵隧道進行沉降預測。由圖3可知，隨著時間的變化，單純的灰色模型預測結果的偏差越來越大，而閾值法小波去噪能提高灰色模型的預測精度，彌補了灰色模型的不足，說明小波去噪與灰色模型組合應用于變形監(jiān)測是可行的，且精度更高。

圖3 成果預測對比圖

4 結 語

灰色模型計算簡單、應用廣泛，短期內(nèi)預測具有明顯優(yōu)勢。利用閾值法小波去噪能大大提高灰色模型的預測精度，彌補灰色模型無法長期預測的不足，極大地增強了灰色模型在工程應用中的實用性。本文驗證了小波去噪與灰色模型的組合模型應用于高鐵隧道沉降監(jiān)測的可行性，為高鐵隧道變形監(jiān)測提供了一種新的思路。