履帶起重機行走部件尺寸匹配方法研究與仿真

張瑞武 王昌磊 滕儒民 李自軍 王 欣

1大連理工大學機械工程學院 大連 116000 2湖南中聯重科履帶起重機股份有限公司 長沙 410000

0 引言

履帶起重機用于物料運輸、裝卸和安裝等作業，具有起重能力強、接地比壓小、轉彎半徑小、爬坡能力大、不需支腿、帶載行走、作業穩定性好等特點。履帶行走的平穩性對減少運動沖擊、載荷沖擊具有至關重要的影響。如果履帶起重機驅動輪與履帶板之間嚙合不好，會造成啃齒及整機抖動現象，影響操作者的舒適性，也不利于起重機的工作性能，故對兩者尺寸的運動匹配性研究十分必要。

業界學者在履帶行走方面開展了充分研究。諸文農等[1]推導了履帶板與驅動輪尺寸的計算方式，根據履帶式機械自重確定履帶板節距，結合驅動輪齒數，獲取驅動輪節圓尺寸。鮑曉杰[3]提出通過調節驅動輪與履帶板間的嚙合尺寸來解決啃齒的方法。崔雪斌[4]通過動力學分析得出通過減小履帶鏈節距，減小鏈環不均勻系數使履帶行走機構獲得更好平穩性的方法。盧進軍[5]利用RecurDyn軟件建立履帶車輛多體動力學模型，為履帶車輛轉向性能的研究與高速轉向的正確操作提供指導。

這些研究在工程機械應用廣泛，為各類履帶車輛底盤設計以及相關優化提供理論基礎。目前，更多是基于理想尺寸下的研究，而實際尺寸的公差對行走機構的平穩性影響至關重要。為此，本文以履帶起重機行走機構為例，根據驅動輪與履帶板的理想嚙合條件，分析兩者的公差配合，提出避免啃齒的尺寸條件，通過不同算例對比分析以及仿真驗證計算方法。

1 履帶行走機構工作原理與理想嚙合條件

履帶起重機行走機構的工作原理是由發動機提供動力，驅動行走馬達旋轉，帶動驅動輪轉動，通過驅動輪與履帶板的槽齒嚙合，最終將驅動輪的旋轉運動轉為履帶板在地面的直線運動。

在理想情況下，履帶板與驅動輪嚙合時可看作履帶板圍成的多邊形內切于驅動輪的直徑，如圖1所示。根據圓與多邊形的幾何關系，可得履帶板節距與驅動輪直徑的關系為

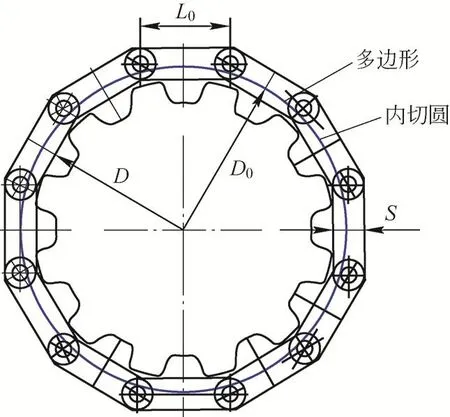
圖1 履帶板節距與驅動輪直徑關系（理想情況）

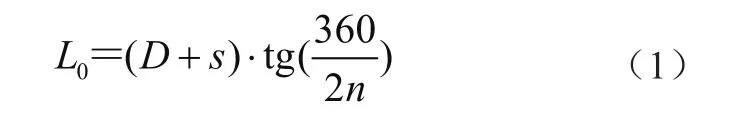
式中：L0為履帶板節距，D為驅動輪直徑，s為履帶板厚度，n為驅動輪槽的數量。

理論上希望驅動輪與履帶板如同精密傳動一般完美嚙合，即在履帶板張緊情況下，驅動輪接近一半的槽與履帶板齒處于嚙合狀態。這就需要履帶板的軸孔配合公差為零，履帶板節距與驅動輪直徑關系恰好為理想狀態。在實際情況下，履帶板與驅動輪都是鑄件，不可避免地存在鑄造誤差或鑄造后的加工誤差，難于實現多對齒槽嚙合，往往只有一對齒槽嚙合。尺寸誤差的進一步加大，會出現啃齒即齒槽嚙合和脫開不順暢現象，同時會伴隨有履帶的抖動現象以及履帶板在地面處的堆積情況。因此，公稱尺寸下的履帶板與驅動輪不啃齒，并不能保證考慮公差時也不啃齒，故需研究履帶板與驅動輪兩者不啃齒條件下的公差配合關系。

圖2、圖3分別為履帶行走時的啃齒與履帶板堆積的模擬。這些現象不僅與履帶板與驅動輪的尺寸誤差有關，還與各履帶板之間的軸孔公差有關。履帶板軸孔公差過大時，會導致履帶板脫離嚙合后的不順暢，從而引起履帶板在地面處的堆積。

圖2 履帶板啃齒模擬

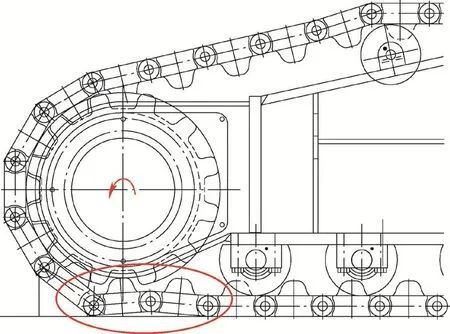
圖3 履帶板堆積模擬

由上述分析可知，為了減少啃齒現象，實現履帶板與驅動輪的順暢嚙合，需要考慮的尺寸公差有：履帶板節距公差、履帶板孔公差、履帶板軸公差、驅動輪直徑公差等。

2 已知驅動輪直徑公差時的履帶板節距公差分析

在不考慮尺寸公差的理想嚙合狀態下，若驅動輪轉動方向如圖4所示，履帶板齒后面和驅動輪槽后面應剛好接觸（圖4中位置3）。為了在此接觸面上不發生啃齒，應使履帶板實際節距L≤L0，L0為理想狀態下的履帶板節距。

圖4 履帶板齒與驅動輪槽的嚙合示意

如果履帶板實際節距過小，會引起履帶板齒前面和驅動輪槽前面的接觸（圖4中位置4），導致前面啃齒。考慮履帶板齒與驅動輪槽存在間隙，表示為p-b，（見圖5），當嚙合在最不利位置時（由于尺寸誤差，通常只有一對齒槽嚙合），即在驅動輪下方接近地面處（圖4中位置5），此時齒和槽后面完全接觸，由于履帶板節距小，存在齒槽間的誤差，并逐漸累積到驅動輪上方履帶板齒要進入槽的位置，則在該位置處不發生齒和槽前面（圖4中位置4）接觸的條件是

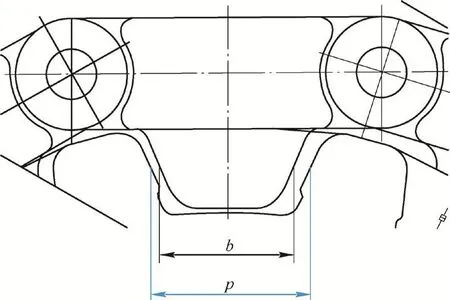
圖5 履帶板齒寬和驅動輪槽寬

由此，為不發生履帶板齒進入驅動輪槽時的前后啃齒現象，根據驅動輪直徑確定的履帶板節距公差范圍為

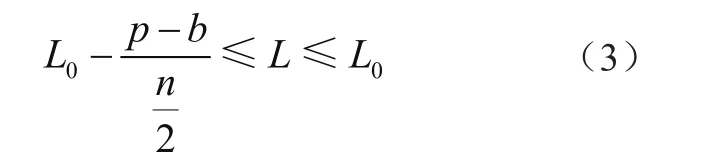
驅動輪直徑也有公差范圍，可根據式（3）分別計算出驅動輪最小公差直徑和最大公差直徑時的履帶板節距公差范圍，然后取這兩種情況下履帶板節距公差范圍的重疊范圍，作為履帶板實際節距最終的公差范圍為

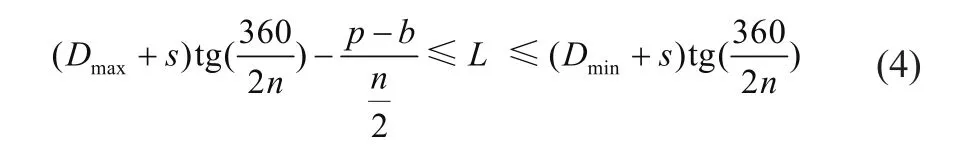
履帶板實際節距與履帶板軸孔公差和履帶板兩孔中心間距有關，如圖6所示，可根據式（5）確定單個軸孔公差范圍之和Δe，其中，ΔL為履帶板兩孔心間距正公差，可表示為

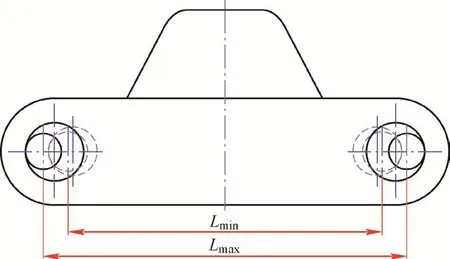
圖6 履帶板的實際節距范圍[Lmin,Lmax]

如果已知履帶板節距公差，可根據嚙合條件推得驅動直徑的公差范圍。由式（1）可得理想嚙合條件下的驅動輪直徑，即

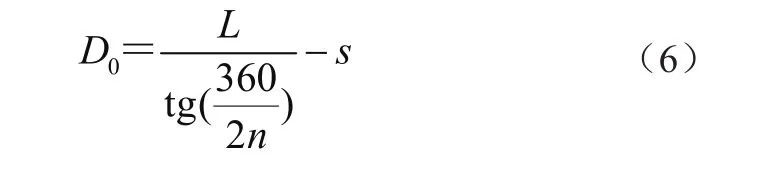
式中：D0為驅動輪直徑。

為了不出現齒與槽的后面啃齒，應使驅動輪直徑D≥D0。考慮履帶板節距的公差，驅動輪直徑應大于最大公差下的履帶板節距推得的驅動輪直徑，即

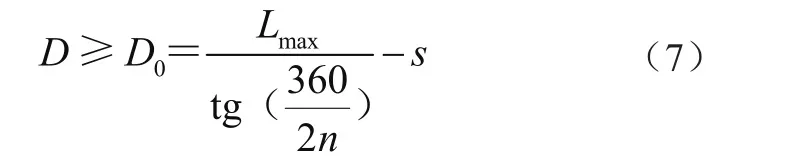
由于齒和槽間隙（p-b）較大，出現齒和槽的前面啃齒幾率較低，但如果設計不當，也要考慮驅動輪最小直徑的要求，見式（8）。由此聯立式（7）和式（8）可得到驅動直徑的公差范圍。

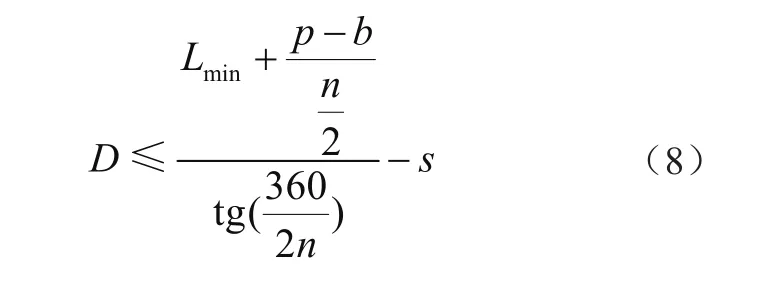
3 算例分析

以實際運動出現啃齒差的某型號履帶起重機產品為例，根據履帶板節距公差來推導驅動輪直徑公差。已知履帶板節距為250±1 mm，履帶板孔徑為φ410+1.5mm，銷軸直徑為φ40 mm，可推得履帶板實際節距公差范圍Lmin＝250 mm，Lmax＝253.5 mm，驅動輪上有12個槽，即n＝12，根據嚙合尺寸，圖示5中的p＝136 mm，b＝111 mm，履帶板厚度s＝90 mm。代入式（7）、式（8）得

給定的驅動輪直徑為φ850±2 mm，沒有在本計算范圍內，故發生了啃齒現象。根據計算結果，將驅動輪直徑改為，經實際運行試驗，未發生啃齒現象。

4 運動仿真分析

根據算例中的某型號產品下車行走機構（見圖7a）在Recurdyn軟件中建立運動仿真模型（見圖7b），代入改進前后的驅動輪直徑尺寸，其他尺寸保持不變，模擬發動機轉速為1 700 r/min的行走后退工況，運行速度在0.46 m/s ，可得改進前后驅動輪中心處的豎直方向加速度曲線，如圖8所示。由此可知，改進前的加速度波動幅度較大，在±1 m/s2之間，這是由啃齒引起的。改進后的加速度在±0.2 m/s2之間，波動幅值明顯減小，仿真中沒有啃齒現象，履帶板齒能順利落在驅動輪槽內。由此通過仿真，再次驗證了前面計算分析的合理性。

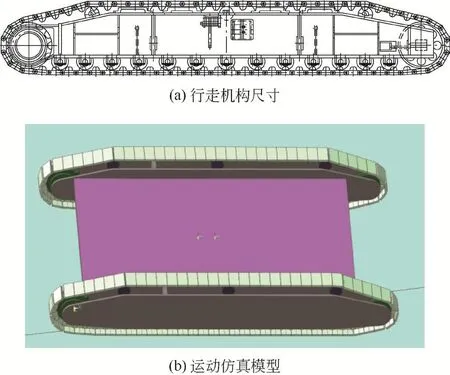
圖7 產品行走機構模型

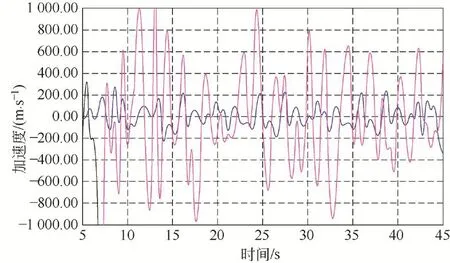
圖8 驅動輪加速度曲線

5 結論

根據履帶行走的工作原理，分析理想尺寸下的履帶板與驅動輪的嚙合條件。根據不啃齒的條件，確定兩者公差帶之間的關系，通過實際算例及運動仿真，表明本文提出的履帶板與驅動輪的尺寸匹配方法的合理性，為相關的尺寸設計提供了理論基礎。