數學分析法在水庫塌坑預測中的應用

□王桂青

陡河水庫處于三面環山的半丘陵地帶，壩頭東岸與鳳山相接處，山體為寒武紀灰巖、夾有灰質和泥質頁巖，多斷層，裂縫，喀斯特發育，自1998 年以來，在水庫東岸水面線附近發生塌坑6次。為探測山體滲漏情況，在鳳山山腳滲漏嚴重部位埋設測壓管12 根，通過測壓管水位與其影響因素的統計分析，力求找到它們的變化規律，并用數學模型表達出來，對東岸山體滲漏情況進行預測。

1.樣本選取

陡河水庫鳳山山腳測壓管水位的可能影響因素為庫水位和降雨量，根據近20 年觀測資料分析，陡河水庫年庫水位變化范圍在30.61～33.39m 之間，年平均降雨量678mm，2005 年庫水位變化范圍在30.67～32.81m 之間，年降水量595.4mm，接近正常年份平均值，選取2005 年部分庫水位、降雨量和測壓管水位觀測數據作為樣本，能夠滿足參數估計量的無偏性、有效性、一致性。

圖1 2005 年陡河水庫山區測壓管水位、庫水位、降雨量過程線

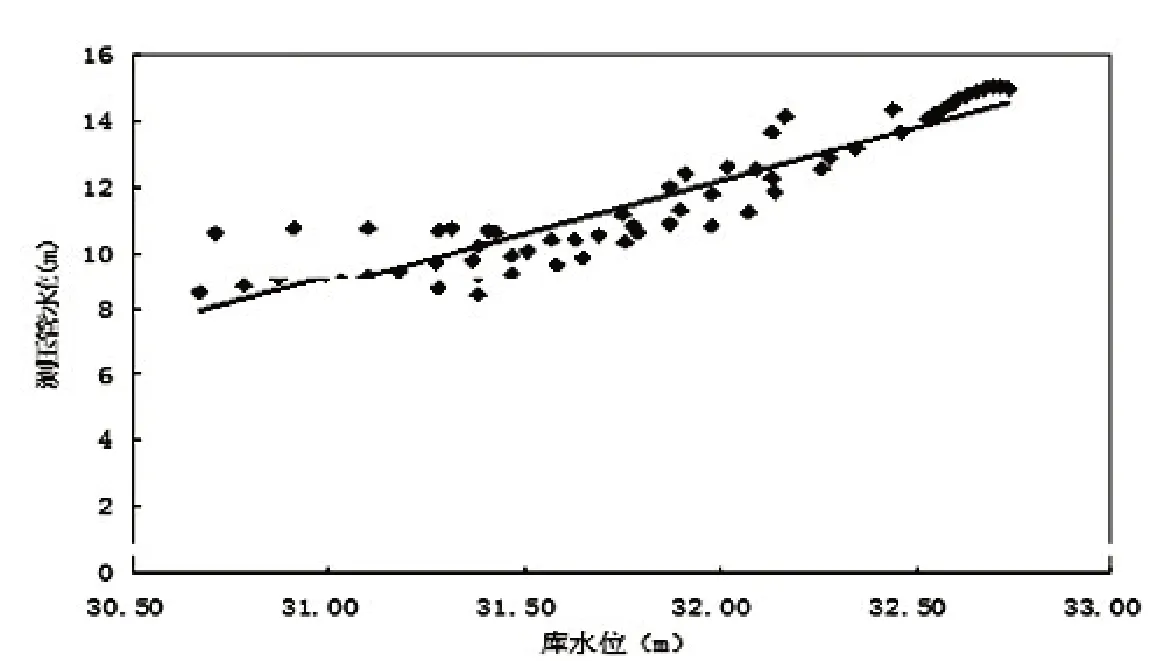
圖2 庫水位與22 號測壓管水位散點圖

2.回歸分析

2.1 影響因素分析

對樣本數據進行分析，繪制出11、13、15、18、22 號測壓管水位過程線，2005 年陡河水庫山區管水位、庫水位、降雨量過程線見圖1。

從圖1 可以看出，各測壓管水位隨庫水位的變化而變化，受降雨量的影響很小。通過近20 年的觀測資料分析，只有2012 年7、8 月東岸山區測壓管水位受降雨影響明顯。所以只研究測壓管水位和庫水位兩個變量的統計規律，在大多數年份是適應的。由于各測壓管水位與庫水位的變化關系相似，所以只選取22 號管作為代表進行分析。

2.2 數學模型確立

選取 62 組 2005 年 22 號測壓管水位與庫水位數據，見表1。把庫水位xa作為橫坐標，測壓管水位ya作為縱坐標，在平面直角坐標系繪出其散點圖，庫水位與22 號測壓管水位散點圖見圖2。這些點大致分布成一條直線，庫水位與22 號測壓管水位之間的關系基本上看作是線性關系，其數學模型假設為ya=β0+βxa，β0、β 為參數。

2.3 參數 β0、β 的估計

根據最小二乘原理，計算出

于是參數 β0、β 的最小二乘估計b0、b 分別為：

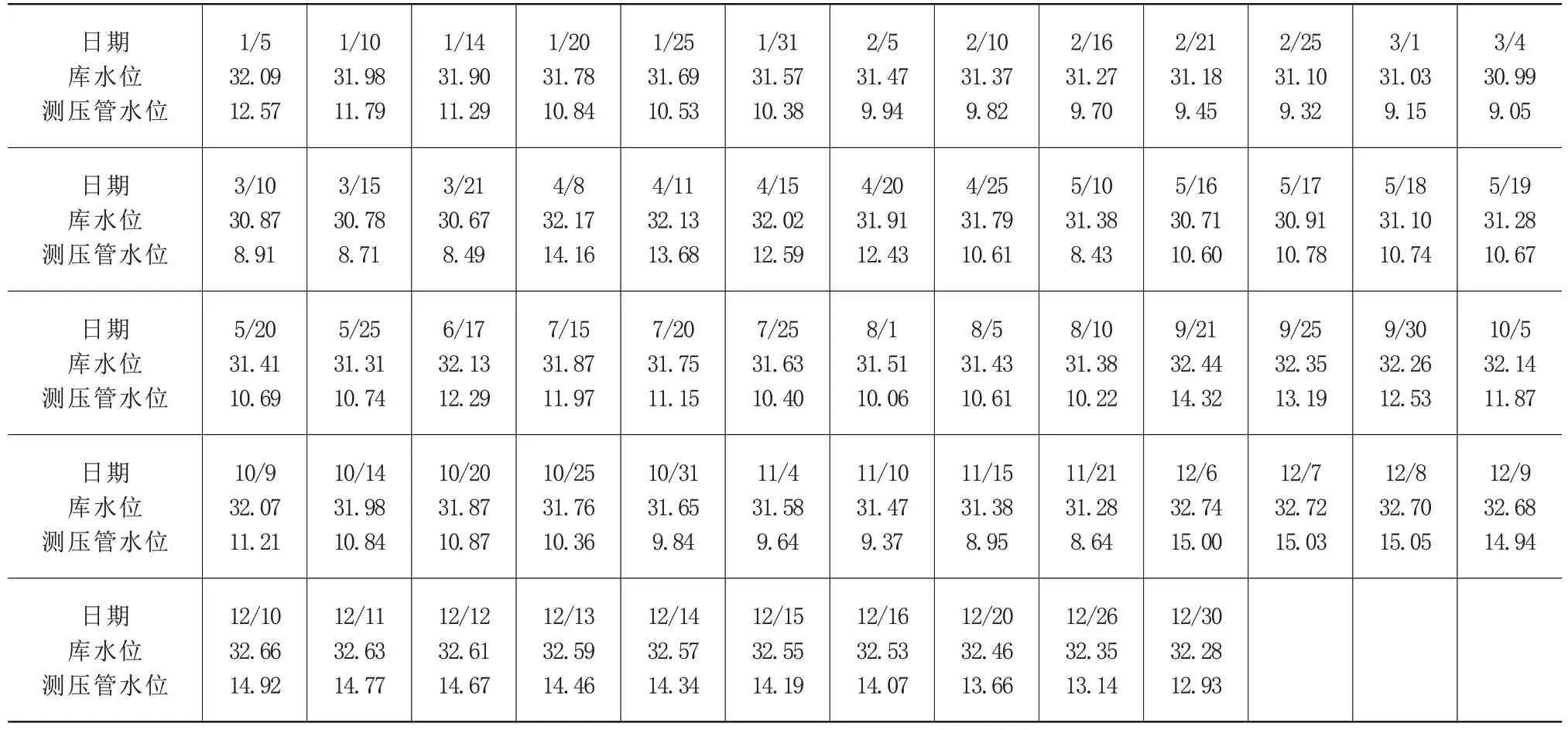
表1 2005 年22 號管水位與庫水位數據

表2 陡河水庫塌坑過程測壓管水位異常情況分析表

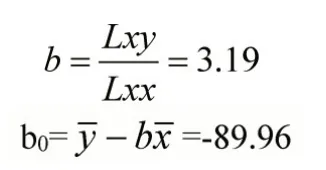
于是得到測壓管水位對庫水位的回歸方程為：

3.假設的顯著性檢驗

由于選擇的模型不夠完善，以及觀察和測量誤差等原因，需要判斷xa與ya之間是否真正具有線性相關關系，對回歸直線的顯著性進行檢驗。如果變量xa與ya之間無線性關系，那么模型中一次項系數 β=0，在 β=0 的條件下，表 1 中統計數據服從自由度為1 和N-2 的F 分布。對實測值 y1、y2、y3……yn 的分散程度進行分析，檢驗假設H0：β=0 是否成立。檢驗公式如下：

式中：

S總—總的偏差平方和；

S回—回歸平方和；

S剩—剩余平方和。

由給定的顯著水平α=0.95，查自由度為(1，62-2)的F 分布臨界值表得臨界值 λ=4.00。由于 F=303.49＞4.00，所以假設 H0：β=0 不成立，xa與 ya之間具有線性關系，并且直線回歸是顯著的。

4.測壓管水位預測

由顯著性檢驗可知，回歸方程擬合得很好，表明測壓管水位與庫水位相關關系密切。可以利用相關方程預報各庫水位對應的測壓管水位。在顯著水平α 下，確定一個預測區間，使實測測壓管水位y0以1-α 的概率落在區間內，對于 α=0.95，查自由度N-2＝60 的t 分布臨界值表，得到λ=2.00，方差 的 估計值測壓管水位 y0的預測區間為

5.東岸塌坑預測

由樣本數據確定回歸方程的過程中，庫水位xa的值波動較大，參數β 的值確定較精確，觀察數據的個數N 有62組，數量較多，由此確定的回歸系數β0也較精確。由圖1 可見，測壓管水位與庫水位過程線變化相似，較庫水位滯后時間不明顯，所以計算得出的測壓管水位觀測值預報區間，能夠反映測壓管水位的正常值變化范圍。如果實測值超出預測區間，山腳有95%的概率發生塌坑。由于很少有外界水源滲流到東岸山體，地下水位的變化主要受庫水位的影響，所以通過庫水位得出的測壓管水位預測區間，與實測測壓管水位相比，可以預測東岸塌坑的發生，這種預測方法已經在多次塌坑中得到檢驗。陡河水庫塌坑過程測壓管水位異常情況分析表見表2。從表2 可見，每次出現塌坑在發現之前，都有測壓管水位實測值高于預測上限值現象，證明東岸塌坑用數學分析方法是可以預測的。

6.結語

通過對陡河水庫實測庫水位和測壓管水位的整理分析，建立二者之間的回歸關系，對東岸山體的測壓水位作出合理預測，用數學計算的方法預測出東岸是否會有塌坑發生，這種方法預測結果準確，使用簡便，能夠及時發現陡河水庫東岸塌坑，減少水庫的滲漏損失。