空時分數階Phi-4方程的新精確解

黃 春

(四川職業技術學院 教師教育系，四川 遂寧 629000)

近年來，分數階偏微分方程在量子力學、通信、控制理論、流體力學、等離子體物理等眾多領域有著廣泛的應用，尋找分數階偏微分方程的精確解一直以來是數學工作者的重要研究課題.構建分數階偏微分方程精確解的方法主要包括：exp-函數法[1-3]、(G’/G)-展開法[4-6]、F-展開法[7-8]、首次積分法[9-12]等。

考慮如下空時分數階Phi-4方程[13-16]：

(1)

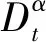
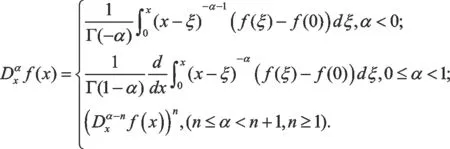
(2)

它具有如下性質：

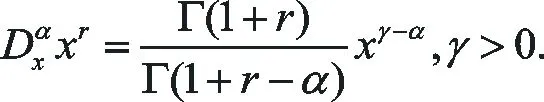
(3)

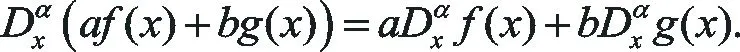
(4)

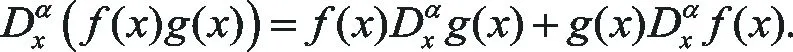
(5)

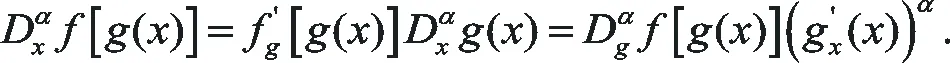
(6)

空時分數階Phi-4方程是一類重要的數學模型，在粒子物理和核物理中占有重要的地位.本文擬用Riemann-Liouville分數階導數與首次積分法相結合，得到空時分數階Phi-4方程的新精確解.

1 方法簡述

定理1.1(除法定理)[19]假設P(w，z)，Q(w，z)是復數域C(w，z)上的多項式，并且P(w，z)在C(w，z)上是不可約的.如果Q(w，z)包含P(w，z)的全部零點，那么在復數域C(w，z)上存在一個多項式G(w，z)使得

Q(w，z)=P(w，z)G(w，z)

(7)

下面是首次積分法求解分數階偏微分方程的主要步驟.考慮如下分數階偏微分方程：

(8)

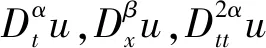
步驟1 作復變換

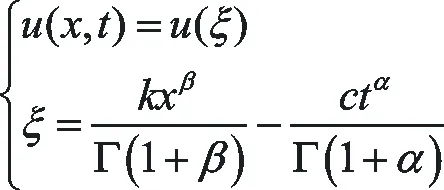
(9)

這里k，c為常數.

將(9)式代入方程(8)中，方程(8)轉化為只含變量ξ的常微分方程：

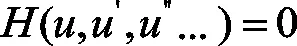
(10)

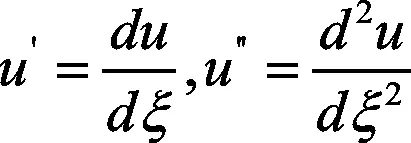
步驟2引入兩個新的獨立變量X(ξ)=u(ξ)，Y(ξ)=u′(ξ)，則方程(10)等價于一階常微分方程組

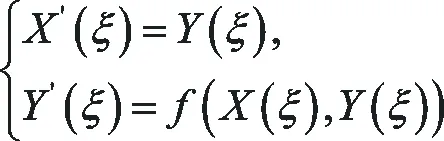
(11)

步驟3設(11)式的首次積分形式為：

(12)

這里ai(X)(i=0，1，2，…，m)是實數域上的待定多項式.根據除法定理，存在實數域上的多項式g(X)，h(X)，使得

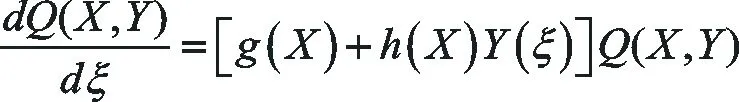
(13)

由(13)式可以確定多項式g(X)，h(X)，進而求出Q(X，Y)

步驟4將X(ξ)=u(ξ)，Y(ξ)=u′(ξ)代入(12)式，解之即得到方程(8)的精確解.

2 運用與結果

對方程(1)作復變換，方程(1)轉化為整數階常微分方程：

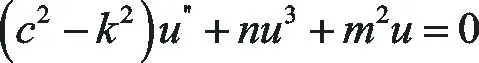
(14)

令X(ξ)=u(ξ)，Y(ξ)=u′(ξ)則方程(14)等價于

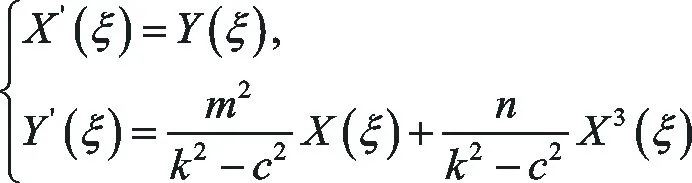
(15)

由首次積分法，假定X(ξ)和Y(ξ)是方程(16)的非平凡解，則方程組(15)的首次積分形式為

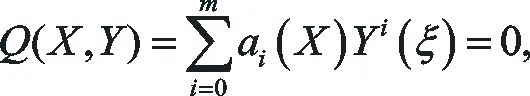
(16)

其中ai(X)(i=0，1，2，…，m)關于X(ξ)的多項式且am(x)≠0.根據除法定理，存在復數域上的多項式g(x)+h(x)Y(ξ)，使得

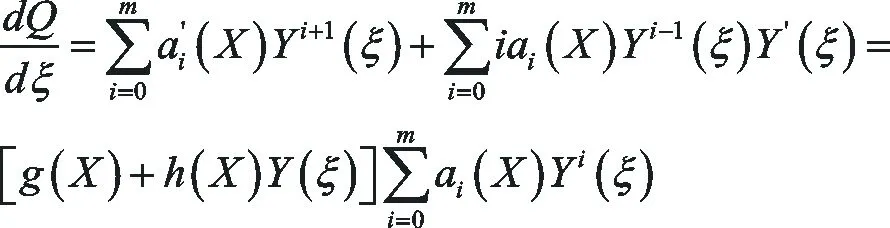
(17)

僅考慮(17)式中的兩種情況，即假定m=1和m=2.

情形1 當m=1時，則有

Q[X，Y]=a0(X)+a1(X)Y(ξ)

(18)

將(18)式代入(17)式后比較等式兩邊Yi(i=0，1)的系數可得

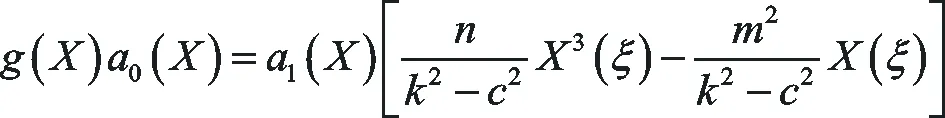
(19)

(20)

(21)

因ai(X)(i=0，1)是關于X(ξ)的多項式，由(21)式可知ai(X)必是一個常數且h(X)=0.為運算簡便，不妨取a1(X)=1.通過平衡(19)式中過g(X)和a0(X)的次數，可得deg[g(X)]=1，deg[a0(X)]=2.假設g(X)=A1X+B0，且A1≠0，則有

(22)

其中A0為積分常數.

將a0(X)，a1(X)，g(X)代入(19)式并比較Xi(ξ)對應項的系數可以得到

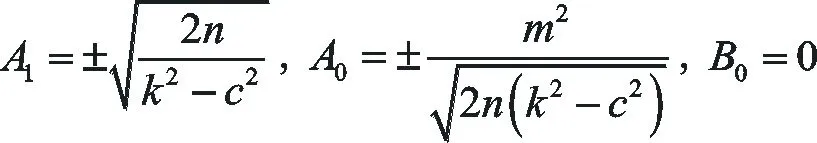
(23)

從而(15)式有下面的首次積分：

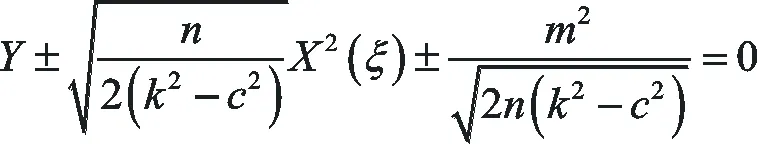
(24)

將X(ξ)=u(ξ)，Y(ξ)=u′(ξ)代入(24)式有

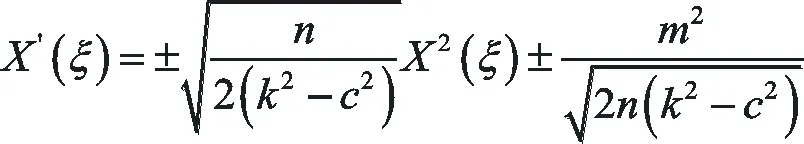
(25)

方程(25)是著名的Riccati方程，即V′(ξ)=α0+α1V(ξ)+α2V2(ξ)，其中α0，α1，α2是常數，α2≠0，Riccati方程有以下解：

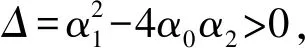
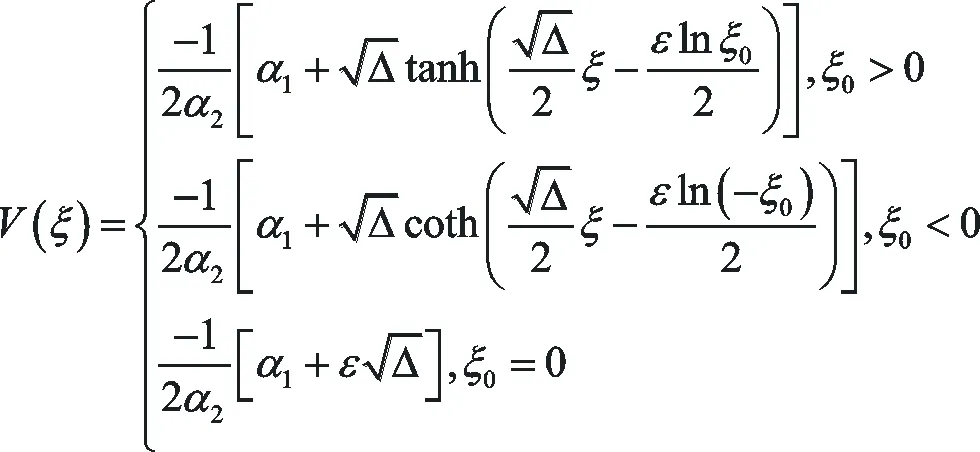
(26)

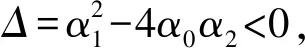
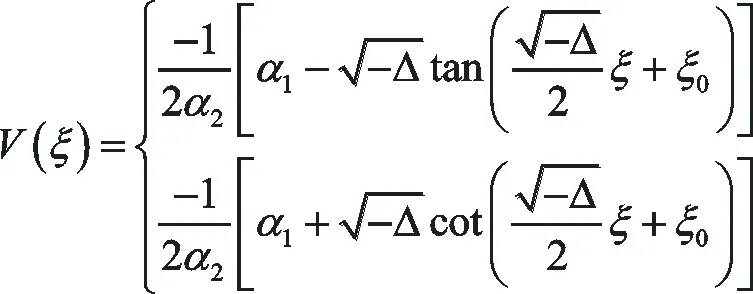
(27)

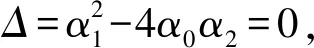
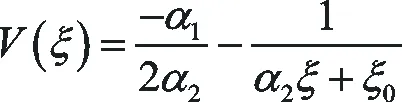
(28)

其中ξ0是任意常數，ε=±1.由(26)-(28)式可得：

大連港、天津港：目前美國航線規模較小，初步測算，吞吐量直接受沖擊的程度低于其他干線港。但由于近年來兩港美線發展緩慢的原因，除腹地經濟結構和產品結構影響外，更是受到釜山港美國航線的強力壓制。隨著美國航線運量受沖擊，釜山港對環渤海等港口的競爭壓力有可能進一步加劇。

(ⅰ)當k2-c2<0，n<0時，方程(1)有如下形式的精確解：

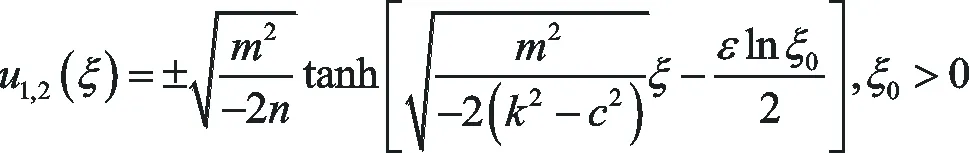
(29)

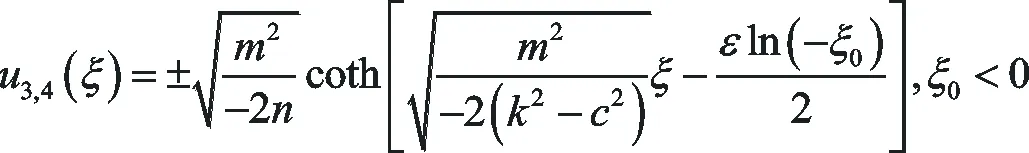
(30)

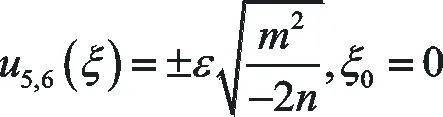
(31)

(ⅱ)當k2-c2>0，n>0時，方程(1)有如下形式的精確解：

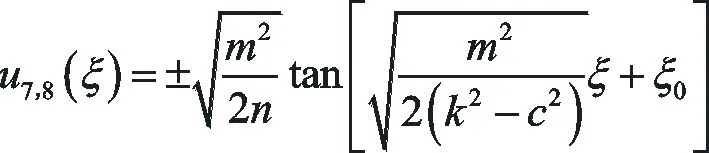
(32)

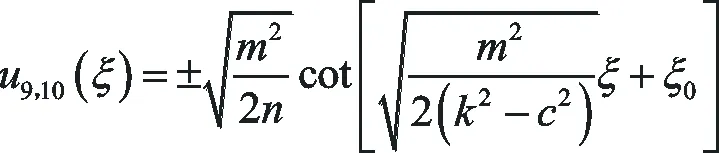
(33)

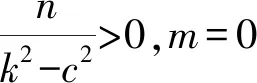
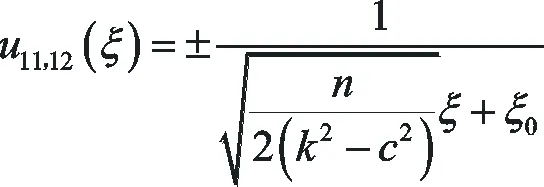
(34)

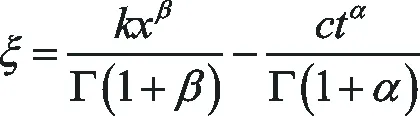
情形2 當m=2時，即

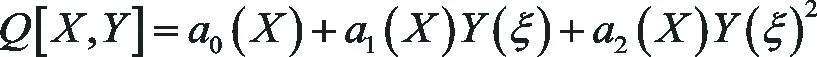
(35)

將(35)式代入(18)式比較等式兩邊Yi(i=0，1，2)的系數可得

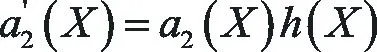
(36)

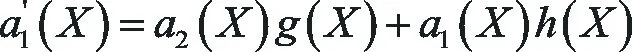
(37)

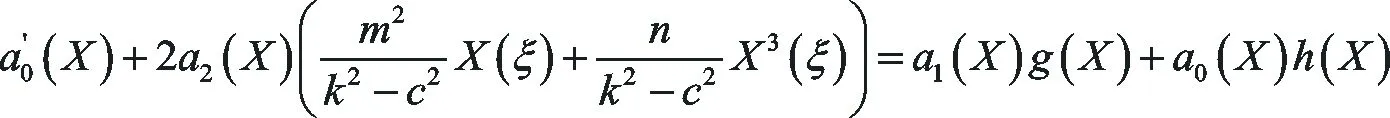
(38)

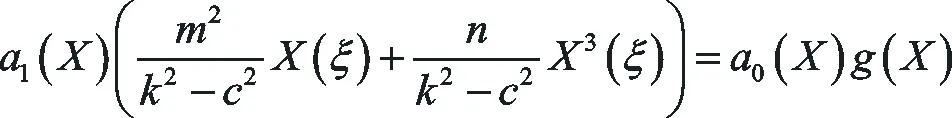
(39)

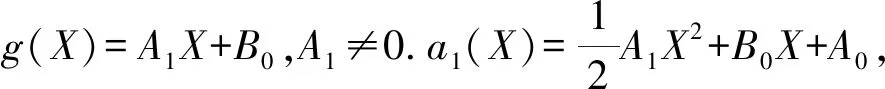
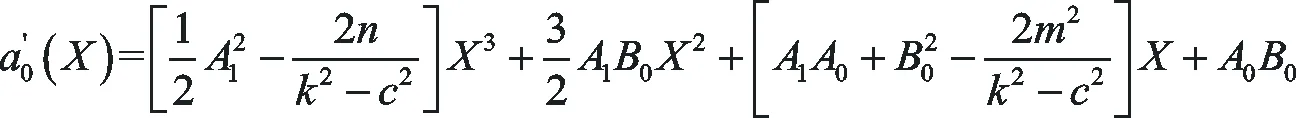
(40)

將上式積分一次可得

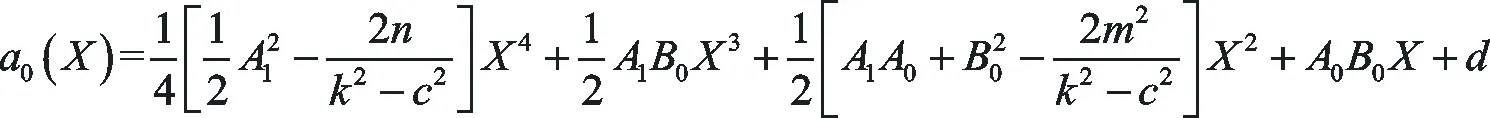
(41)

這里的d為積分常數.

將a0(X)，a1(X)和g(X)及代入(39)式并比較Xi(ξ)的對應項系數得到

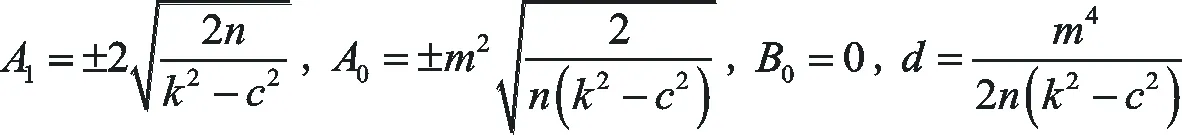
(42)

因此可得

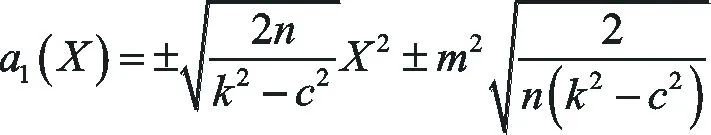
(43)

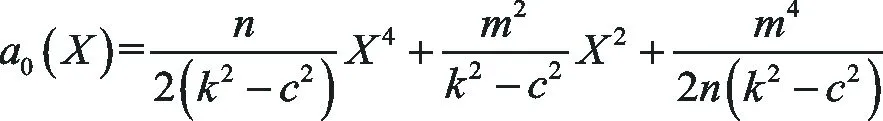
(44)

將(43)和(44)式代入(35)式化簡可得

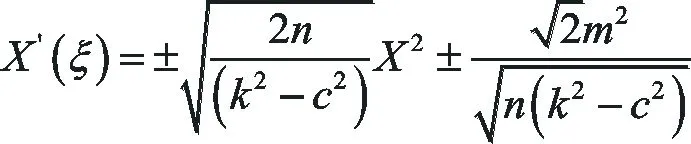
(45)

聯立(25)和(45)式，運算可知m=1與m=2的情況相同.為了更直觀的理解這些解，借助Maple軟件得到解的數值模擬圖像如圖1-4所示.

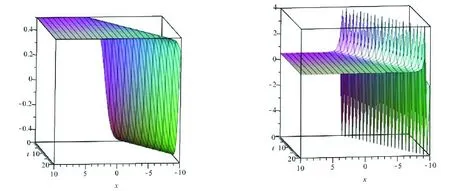
圖1 當m=1，n=-2，k=1，c=2，ε=1，ξ0=1，時，u1(ξ)的三維圖 圖2 當m=1，n=-2，k=1，c=2，ε=1，ξ0=-1，時，u3(ξ)的三維圖

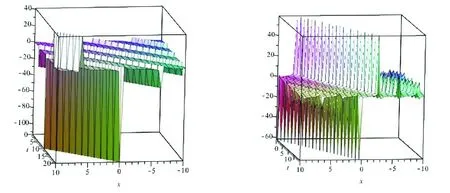
圖3 當m=1，n=2，k=2，c=1，ξ0=1，時，u7(ξ)的三維圖 圖4 當m=1，n=2，k=2，c=1，ξ0=1，時，u9(ξ)的三維圖

3 結論

本文借助Riemann-Liouville分數階導數，基于首次積分法構建空時分數階Phi-4方程的新精確解，其中u1，2(ξ)為扭狀孤立波解，u3，4(ξ)為奇異孤立波解，u7，8(ξ)、u9，10(ξ)為周期波解，u5，6(ξ)、u11，12(ξ)為有理函數解，豐富了其精確解解系.這也說明首次積分法是求解分數階偏微分方程的一種有效的工具且簡單易行。