具有非線性發生率的諾如病毒傳播動力學模型分析

秦海燕 侯強

摘 要：為了減少因諾如病毒感染引起的感染性腹瀉對人們身體健康造成的危害，在明確諾如病毒傳播特征的基礎上，研究了諾如病毒的傳播動力學行為，考慮感染諾如病毒的潛伏者也傳染疾病的特性，建立具有非線性發生率的諾如病毒傳播動力學模型，在計算模型的基本再生數R0的基礎上，利用Lyapunov函數和幾何方法證明了無病平衡點和地方病平衡點的穩定性，并進行了數值模擬。結果表明，當R0≤1時，無病平衡點全局漸近穩定，疾病消失;當R0>1時，在一定條件下，地方病平衡點全局漸近穩定。數值模擬驗證了理論結果的正確性。研究結果豐富了感染性病毒傳播理論，對進一步研究病毒的傳播機理具有借鑒意義。

關鍵詞：穩定性理論;諾如病毒;傳染病模型;非線性發生率;基本再生數

中圖分類號：O175.1 文獻標識碼：A

doi：10.7535/hbkd.2021yx02005

Dynamic model analysis of Norovirus transmissionwith nonlinear incidence

QIN Haiyan，HOU Qiang

（School of Science，North University of China，Taiyuan，Shanxi 030051，China）

Abstract：In order to reduce the great harm of infectious diarrhoeal disease caused by Norovirus infection to human health，based on the transmission characteristics of Norovirus，the transmission dynamics behavior of Norovirus was studied.Taking into account the characteristics that the latent infected with Norovirus can also transmit the disease，a dynamic model of Norovirus transmission with nonlinear incidence was established.The basic reproduction number R0of the model was calculated and then the stability of the disease-free equilibrium point and the endemic equilibrium point were proved by using the Lyapunov function and the geometric method.The results show that when R0≤1，the disease-free equilibrium point is globally asymptotically stable and the disease disappears; when R0>1，under certain conditions，the endemic equilibrium point is global asymptotically stable.The theoretical results are verified by numerical simulation.The research results have enriched the theory of infectious virus transmission and provide a reference for the study of virus transmission mechanism.

Keywords：

stability theory;Norovirus;infectious disease model;nonlinear incidence;basic reproduction number

諾如病毒是全球急性腸胃炎的主要致病原，致人感染發病的主要表現為腹瀉和嘔吐，其傳播途徑包括人與人之間的傳播和食源性傳播。人傳人通過糞口途徑傳播（包括吸入糞便或嘔吐物產生的氣溶膠），食源性傳播通過食用被諾如病毒污染的食物和水進行傳播。諾如病毒變異很快，對環境的抵抗力也很強，感染后潛伏期較短，且在潛伏期便可排出病毒，排毒時間長，免疫保護時間卻較短[1-9]。自2013年以來，感染性腹瀉病暴發大多以諾如病毒感染為主，尤其是自2014年冬季起，諾如病毒的感染暴發疫情有較大幅度增加，顯著高于歷年水平[10-11]。

近年來，許多學者對諾如病毒的傳播動力學進行了研究[12-14]。史方等[15]根據諾如病毒的流行病學特點建立模型，利用實測數據估計了模型中的參數，分析了潛伏期內的新發感染者、新發病人和新發無癥狀感染者之間的關系，研究了不同傳染源在疾病傳播研究過程中的貢獻率，以及外部干預措施對諾如病毒傳播的影響;GAYTHORPE等[16]根據年齡分層建立時間序列模型，研究發現，接種疫苗是預防疾病的有效策略;黃璜等[17]通過比較各模型評價隔離措施對諾如病毒在醫院內傳播的影響，為有效防控諾如病毒在醫院內的感染暴發提供理論依據;LANE等[18]研究了諾如病毒通過人與人之間的傳播和食源性傳播導致人產生感染性腸道疾病，并進一步了解食源性如何傳播諾如病毒。

目前的研究中，較少人考慮諾如病毒傳播與穩定性相關的動力學性態，因此，筆者根據諾如病毒的流行病學特性，提出了發病率形式為β1fES+β2gIS的SEIRS非線性傳播動力學模型，并運用微分動力系統理論分析模型的穩定性，最后通過數值模擬驗證結果的正確性。

1 模型的建立

將人群分為4類，即易感者S（t）、潛伏者E（t）、染病者I（t）和恢復者R（t）。用N表示總人口，N=S+E+I+R，易感者雖然也可通過攝取被諾如病毒污染的食物而被感染，但本文重點研究潛伏者、染病者對諾如病毒傳播的影響，所以忽略食源性感染。建立如下模型：

dSdt=A-β1fES-β2gIS-μS+δR，dEdt=β1fES+β2gIS-μE-εE，dIdt=εE-μI-γI，dRdt=γI-μR-δR。（1）

式中：A表示人口常數輸入率;β1表示潛伏者的傳染率;β2表示染病者的傳染率;ε表示潛伏者變為染病者的比例;γ表示人的恢復率;δ表示恢復者失去免疫力的比率;μ表示人的自然死亡率。采用一般非線性發生率β1fES+β2gIS表示諾如病毒的傳播發生率。為了滿足模型（1）的流行病學意義，對于發生率函數，假定f0=g0=0，且f′E>0，g′I>0，f″E≤0，g″I≤0，在文獻[17]中，這里的發生率為雙線性發生率β1SE+β2SI。

2 平衡點的存在性和基本再生數

對于模型（1），其可行域為Ω=S，E，I，RS≥0，E≥0，I≥0，R≥0，S+E+I+R≤Aμ。模型（1）有唯一的無病平衡點E0=（S0，E0，I0，R0）=Aμ，0，0，0，根據下一代矩陣法[20]，F=β1f′0S0β2g′0S000，V=μ+ε0-εμ+γ，則模型的基本再生數為R0=ρ（FV-1）=β1f′0S0μ+ε+β2g′0S0εμ+εμ+γ=R01+R02。

為求模型（1）地方病平衡點，令模型（1）的第3個和第4個等式右端為0，則有：

E=μ+γεI;R=γμ+δI。

令模型（1）的前2個等式右端為0，則有：A-μ+εE-μS+δR=0。可得：

S=Aμ-μ+εμ+γμε-δγμμ+δI。

令第1個式子右邊為0，可得：

GI=A-β1fμ+γεI+β2gI+μAμ-k1I+k2I，

其中：k1=μ+εμ+γμε-δγμμ+δ;k2=δγμ+δ。

對G（I）求導可得：

G′I=k2+k1β1fμ+γεI+β2gI+μ-β1μ+γεf′μ+γεI+β2g′IAμ-k1I，

則有：

G′0=k2+k1μ-β1μ+γεf′0+β2g′0Aμ=μ+εμ+γε（1-R0），

又

G″I=2k1β1μ+γεf′μ+γεI+β2g′I-β1μ+γε2f″μ+γεI+β2g″IAμ-k1I，

當I∈0，Ak1μ時，G″I>0，所以G′I單增，又當R0>1時，G′0<0，可得GI先減后增，且G0=0，GAk1μ>0，所以一定存在一個I，使得G（I）=0;當I∈Ak1μ，Aμ時，GAk1μ>0，G′I>0，此時不存在一個I，使得G（I）=0。

因此有結論：當R0>1時，模型（1）存在唯一正平衡點E*（S*，E*，I*，R*），即有：

定理1 對于模型（1）有以下結論：當R0≤1時，模型（1）有一個無病平衡點E0;當R0>1時，模型（1）存在唯一正平衡點E*。

3 平衡點的穩定性

定理2 如果R0≤1，模型（1）的無病平衡點E0在Ω內是全局漸近穩定的;如果R0>1，無病平衡點是不穩定的。

證明 矩陣在E0處的特征方程為（λ+μ）λ+μ+δ（λ2+a1λ+a2）=0。其中：a1=μ+γ+μ+ε1-R01，a2=μ+εμ+γ1-R0。

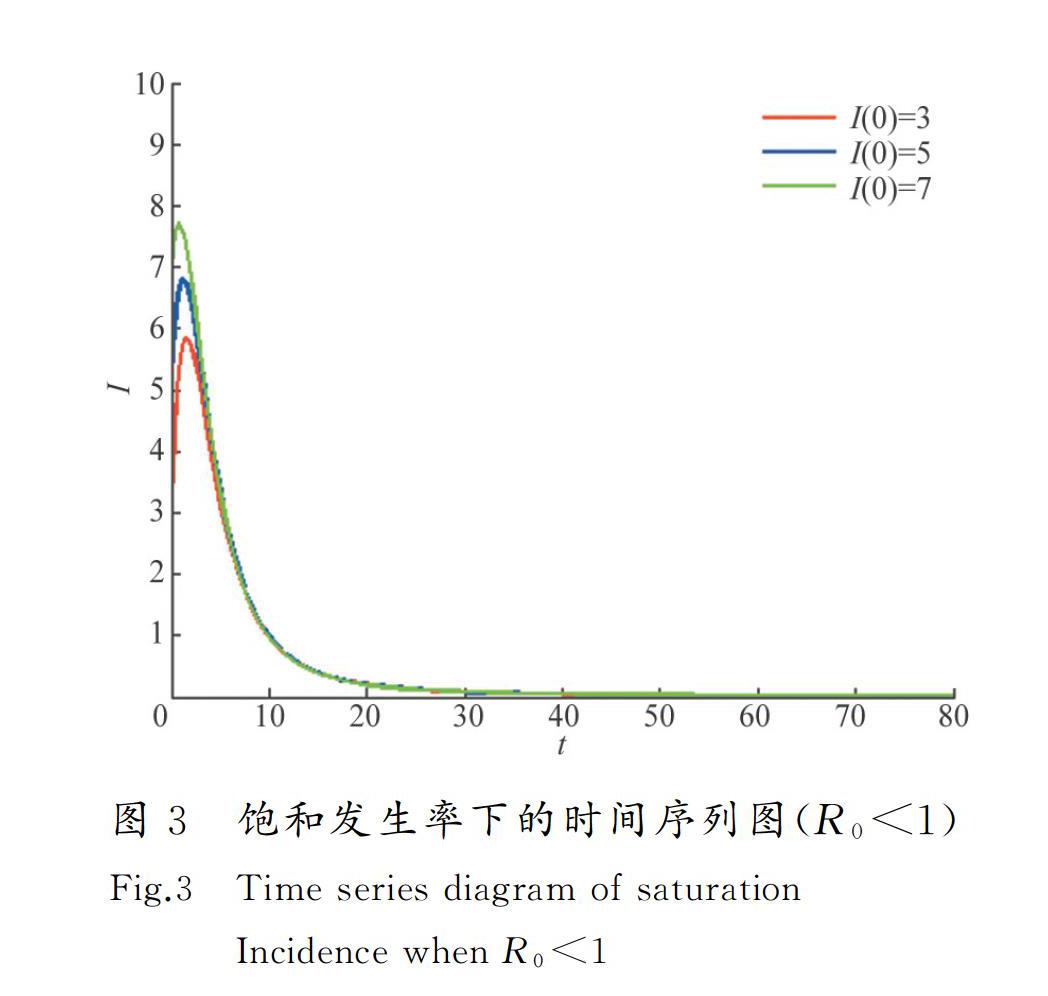
當R0≤1時，a1>0，a2>0，又λ1=-μ<0，λ2=-μ-δ<0，所以模型（1）的無病平衡點是局部漸近穩定的。當R0>1時，有a2<0，這里存在正根，無病平衡點不穩定，構造Lyapunov函數證明無病平衡點的全局漸近穩定性：因為fx在區間0，Aμ上恒有f″x≤0，則對任意的x，y∈0，Aμ滿足x

同理可得：gII′=g′II-gII2=g′I-gIII≤0。所以，fEE和gII為減函數。

因此：β1f（E）S（μ+ε）E≤limE→0β1f′（E）S0（μ+ε）E=β1f′E（0）S0μ+εb1，β2g（I）S（μ+γ）I≤limI→0β2g（I）S0（μ+γ）I=β2g′I（0）S0μ+γb2。

定義 J=10-εμ+ε1，c1，c2=b1，b2J-1。因此，c1=R0≤1，根據（b1，b2）的正性可得（c1，c2）的正性，構造Lyapunov函數L=R0E+c2I。

對L關于模型（1）求導：

dLdt=R0β1fESμ+εE，β2gISμ+γIμ+εE，μ+γIT-R0，c2Jμ+εE，μ+γIT≤

R0β1f′E0S0μ+ε，β2g′I0S0μ+γμ+εE，μ+γIT-R0，c2Jμ+εE，μ+γIT=

R0-1b1，b2μ+εE，μ+γIT。

因此，當R0≤1時，L′≤0，而L′=0的最大不變集包含唯一的點E0=Aμ，0，0，0。由Lasalle不變集原理[19]可知，當R0≤1時，無病平衡點在Ω內是全局漸近穩定的。

由定理2知，如果R0>1，無病平衡點是不穩定的。根據文獻[20]，易證模型（1）的一致持續等價于無病平衡點的不穩定性，故當R0>1時，模型（1）是一致持續的，因此存在一個緊吸引子集K。

因此當t>t*時，可得：

1t∫t0g1ds≤1t∫0t*g1ds-1tlnItI（t*）-b—t-t*t，

1t∫t0g2ds≤1t∫0t*g2ds-1tlnItI（t*）-b—t-t*t，

1t∫t0g3ds≤1t∫0t*g3ds-1tlnItI（t*）-b—t-t*t，

1t∫t0g4ds≤1t∫0t*g4ds-1tlnItI（t*）-b—t-t*t，

則有：

1t∫t0η（Q）ds≤sup1t∫0t*g1ds-1tlnItI（t*）-b—t-t*t，

1t∫0t*g2ds-1tlnItI（t*）-b—t-t*t，

1t∫0t*g3ds-1tlnItI（t*）-b—t-t*t，

1t∫0t*g4ds-1tlnItI（t*）-b—t-t*t。

從而有：

q=lim sup supt→+SymboleB@x∈K1t∫t0η（Q）ds≤ -b—<0，

即當R0>1時，系統（1）的地方病平衡點E*全局漸近穩定。

4 數值模擬

采用數值模擬方法證明模型（1）中非線性發生率分別為雙線性發生率和飽和發生率時，其在無病平衡點和地方病平衡點處的動力學性質。

圖1和圖2是非線性發生率為雙線性發生率β1SE+β2SI時，取不同參數值的數值模擬情況。

參數值如下：

1） μ=0.05，β1=0.006，β2=0.008，δ=0.01，ε=0.5，γ=0.5，A=2。I取初始值I（0）=3，I（0）=5，I（0）=7，此時R0=0.531<1。從圖1中可以看出無病平衡點E0在Ω內全局漸近穩定。

2）μ=0.05，β1=0.01，β2=0.02，δ=0.01，ε=0.5，γ=0.5，A=2。I取初始值I（0）=3，I（0）=5，I（0）=7，此時R0=1.127>1，且模型的雅可比矩陣在地方病平衡點處的特征方程的特征根均具有負實部，因此地方病平衡點E*在Ω內局部漸近穩定，從圖2可以看出地方病平衡點E*在Ω內全局漸近穩定。

參數值如下：

1）μ=0.05，β1=0.006，β2=0.008，δ=0.01，ε=0.5，γ=0.5，A=2，α=0.2。I取初始值I（0）=3，I（0）=5，I（0）=7，此時R0=0.531<1。從圖3可以看出無病平衡點E0在Ω內全局漸近穩定。

2）μ=0.05，β1=0.01，β2=0.02，δ=0.01，ε=0.5，γ=0.5，A=2，α=0.2。I取初始值I（0）=3，I（0）=5，I（0）=7，此時R0=1.127>1，且模型的雅可比矩陣在地方病平衡點處的特征方程的特征根均具有負實部，因此地方病平衡點E*在Ω內局部漸近穩定，從圖4可以看出地方病平衡點E*在Ω內全局漸近穩定。

5 結 語

針對諾如病毒變異快、感染性強、對環境抵抗力強的特性，在一般SEIR模型基礎上，提出了具有非線性發生率的諾如病毒傳播動力學模型，在一般的生物學假設下，分析了平衡點的存在性和穩定性。結果表明，如果R0<1，則無病平衡點全局漸近穩定，這意味著疾病滅絕;如果R0>1，則存在唯一的地方病平衡點且在一定條件下全局漸近穩定。本研究尚未證明地方病平衡點的局部穩定性，這是后續要做的重要工作之一。

參考文獻/References：

[1] LOPMAN B，VENNEMA H，KOHLI E，et al.Increase in viral gastroenteritis outbreaks in Europe and epidemic spread of new Norovirus variant[J].The Lancet，2004，9410（363）：682-688.

[2] YEN C，WIKSWO M E，LOPMAN B A，et al.Impact of an emergent Norovirus variant in 2009 on Norovirus outbreak activity in the United States[J].Clinical Infectious Diseases an Official Publication of the Infectious Diseases Society of America，2011，53（6）：568-571.

[3] GTZ H，EKDAHL K，LINDBCK J，et al.Clinical spectrum and transmission characteristics of infection with Norwalk virus：Findings from a large community outbreak in Sweden[J].Clin Infect Dis，2001，33：622-628.

[4] LEE R M，LESSLER J，LEE R A，et al.Incubation periods of viral gastroenteritis：A systematic review[J].Infect Dis，2013，13：446.

[5] ATMAR R L，OPEKUN A R，GILGER M A，et al.Norwalk virus shedding after experimental human infection[J].Emerg Infect Dis，2008，14：1553-1559.

[6] KIRBY AE，SHI J，MONTES J，et al.Disease course and viral shedding in experimental norwalk virus and snow mountain virus infection[J].J Med Virol，2014，86（12）：2055-2064.

[7] TEUNIS P F，SUKHRIE F H，VENNEMA H，et al.Shedding of norovirus in symptomatic and asymptomatic infetion[J].Epidemiol Infect，2015，143（8）：1710-1717.

[8] AOKI Y，SUTO A，MIZUTA K，et al.Duration of Norovirus excretion and the longitudinal course of viral load in Norovirus-infected elderly patients[J].Hosp Infect，2010，75（1）：42-46.

[9] THOMAS A，PARRINO M D，DAVID S，et al.Clinical immunity in acute gastroenteritis caused by norwalk agent[J].The New England Journal of Medicine，1977，297：86-89.

[10]LU Jing，SUN Limei，FANG Lin，et al.Gastroenteritis outbreaks caused by Norovirus GII.17，Guangdong Province，China，2014—2015[J].Emerging Infectious Disease，2015，21（7）：1240-1241.

[11]HAN J，JI L，SHEN Y et al.Emergence and predominance of norovirus GII.17 in Huzhou，China[J].Virol Journal，2015，12（1）：139.

[12]NEWMAN K L，MOE C L，KIRBY A E，et al.Norovirus in symptomatic and asymptomatic individuals：Cytokines and viral shedding[J].Clin Exp Immunol，2016，184：347-357.

[13]VANDERPAS J，LOUIS J，REYNDERS M，et al.Mathematical model for the control of nosocomial Norovirus[J].Journal of Hospital Infection，2009，71（3）：214-222.

[14]MAESHALL J，BRUGGINK L D.The dynamics of Norovirus outbreak epidemics：Recent insights[J].International Journal of Environmental Research and Public Health，2011，8（4）：1141-1149.

[15]史方，周毅，劉茂華，等.諾如病毒感染的傳播動力學研究[J].中國國境衛生檢疫雜志，2015，38（6）：413-418.

SHI Fang，ZHOU Yi，LIU Maohua，et al.Study on transmission dynamics of Norovirus infection[J].Chinese Journal of Frontier Health and Quarantine，2015，38（6）：413-418.

[16]GAYTHORPE K A M，TROTTER C L，CONLAN A J K.Modelling norovirus transmission and vaccination[J].Vaccine，2018，36：5565-5571.

[17]黃璜，蘭玲，單旭征，等.SEIR模型在諾如病毒醫院感染的應用研究[J].中國醫院感染學雜志，2018，28（14）：2205-2208.

HUANG Huang，LAN Ling，SHAN Xuzheng，et al.Application of SEIR model in nosocomial infection of Norovirus[J].Chinese Journal of Nosocomial Infectiology，2018，28（14）：2205-2208.

[18]LANE D，HUSEMANN E，HOLLAND D，et al.Understanding foodborne transmission mechanisms for Norovirus：A study for the UK's Food Standards Agency[J].European Journal of Operational Research，2019，275：721-736.

[19]LASALLE J P.The stability of dynamical systems[J].SIAM Review，1976，21（3）.doi：10.1137/1021079.

[20]MICHAEL Y L，JOHN R G，WANG Liancheng，et al.Global dynamics of a SEIR model with varying total population size[J].Math Biosci，1999，160：191-213.

[21]MICHAEL Y L，MULDOWNEY J S.A geometric approach to global stability problems[J].Siam Journal on Mathematical Analysis，1996，27：1070-1083.