電機中ABC到dq0坐標變換的梳理與辨析

付興賀，陳 銳

（東南大學 電氣工程學院，南京210096）

0 引 言

近百年來，坐標變換方法已廣泛應用于電氣工程的各個領域，解決三相（甚至多相）交流系統中數學模型表征、多變量解耦及不對稱分量分析等難題［1?2］。隨著智能電網的提出，高品質電機系統的迫切需求，以及高效電能變換的發展，交流電氣系統的結構日漸復雜，坐標變換方法已成為系統設計、建模和分析的重要手段，因此深入理解和正確使用坐標變換方法非常必要。

Clarke變換和Park變換是兩種典型的坐標變換方法，主要用于電機系統建模分析及驅動控制［3?4］、電力系統微電網分析［5?6］和電力電子逆變器建模［7?8］等方面。從數學角度出發，Clarke變換和Park變換實現了機電或電氣系統中物理量在不同坐標系下的表征。目前，廣大工程技術人員及專家學者已基本了解Clarke變換和Park變換，能夠嘗試應用Clarke變換和Park變換，分析交流系統的動態性能。但是，也出現了沒能抓住坐標變換的本質問題、對坐標變換方法使用不當的情況，導致教學和科研工作偏離主題、得出錯誤結果。文獻［9］對坐標系的定義有誤，并且采用坐標變換的假設條件表述不清；文獻［10?17］將Park變換定義為從兩相靜止到兩相旋轉的坐標變換，理解有失偏頗；文獻［16］混淆了等功率和等幅值變換矩陣；文獻［10，15，17］未給出d，q坐標軸的定義，并且混淆了d，q軸的基本概念。文獻［18］雖然點明了坐標變換誤用的問題，但此類現象仍然沒有得到足夠重視。因此，回溯Clarke變換和Park變換的發展歷程，深究Clarke變換和Park變換的本質內涵，對于教學和科研工作具有重要意義和價值。

部分學者試圖從數學角度出發，重新審視Clarke變化和Park變換的推導過程，明確兩種變換的數學意義。文獻［18］在綜合矢量基礎上利用三角函數關系對ABC／αβ0變換進行了數學意義的推導，說明了限制條件；文獻［19?20］在基于空間旋轉坐標的基礎上開展了幾何分析工作，分析過程相對復雜；在三相交流系統的基礎上，文獻［21］提出了四相到任意相交流系統Park變換矩陣推演方式；文獻［22］利用求電感矩陣特征值的方法，解得ABC／dq0變換矩陣，該方法具有一定的普適性。總體而言，上述工作更多的意義在于數學或幾何證明，缺乏物理指導意義，同時也沒有指出坐標變換間的相互關系，沒有指明應用過程的注意事項。在上述工作基礎上，本文旨在繼續加深和完善對Clarke和Park變換的認識，指出兩種變換應用中出現的問題及應對措施。

首先，本文給出了Clarke變換和Park變換的初始定義，揭示了兩種變換的初衷和目的。然后，理論推演了電機分析中常用的三相靜止坐標系、兩相靜止坐標系及兩相旋轉坐標系之間的變換，分析了幾種變換矩陣之間的聯系與差異。接著，指出了應用中存在的混淆坐標定義、誤解坐標變換及使用不當等問題。最后，以永磁同步電機調速系統為例，開展分析和示教工作，驗證不同的變換矩陣及其誤用對系統性能的影響。

雖然本文不屬于技術或方法創新，但通過對坐標變換開展深入細致的梳理與辨析，有助于工程技術人員熟悉坐標變換的發展歷程，理解理論基礎，掌握使用方法。此外，對高等學校教師及學生而言，本文關于坐標變換的歷史探究、相關定義澄清及誤用糾正等方面的嘗試，也將為課堂教學、理論學習和實踐指導等提供借鑒和幫助。

1 Clarke變換與Park變換的初始定義

1.1 Clarke變換

1918年，Fortescue提出了用于分析不對稱三相系統的對稱分量法，即將不對稱的三相分量分解為正序、負序和零序分量。三相的正序、負序分量相序相反，零序分量幅值、相位均相同。1937年左右，Clarke提出了αβ0分量法以改進對稱分量法，簡化了電力系統中不對稱問題的分析。1951年，Clarke指出采用αβ0坐標系可以簡化電機中部分公式的推導過程［1］。因此，她將原來用于電力系統分析的αβ0分量法推廣到同步電機分析中，建立了瞬時相量ABC和αβ0分量、αβ0分量和dq0分量之間的變換關系。隨著坐標變換在電機領域中的廣泛應用，考慮到Clarke的理論貢獻，ABC／αβ0變換逐漸被稱為了Clarke變換。

1.2 Park變換

1899年，Blondel針對凸極同步電機的結構特點提出了雙反應理論，用兩個相對簡單的交、直軸電樞反應描述復雜難解的電樞反應。即將電樞基波磁動勢Fa分解為作用在直軸上的直軸電樞反應磁動勢Fd和作用在交軸上的交軸電樞反應磁動勢Fq［23］。1929年，Park在雙反應理論的基礎上提出了分析同步電機的一般化方法：將磁鏈、電流、電壓等三相物理量等效成隨轉子同步旋轉的直軸分量與交軸分量，消除了變量之間的耦合。根據同步電機方程及ABC與dq0坐標系之間的對應關系，Park推導出由空間靜止的ABC坐標系變換到空間旋轉的dq0標系的變換式，即Park變換。在分析中，一般均假設三相對稱，故0軸略去。因此，Park變換本質上是ABC／dq0的坐標變換方式。

2 電機分析中的坐標變換

2.1 坐標變換的目的

在直流電機中，勵磁繞組軸線方向為主磁通方向，該方向定義為直軸（d軸），電樞繞組產生的電樞磁動勢的軸線方向則被定義為交軸（q軸）。電樞繞組通過位于幾何中性線上的電刷與電源連接，因此，電樞磁動勢的軸線被電刷限定在q軸。d軸與q軸相差90°電角度，d軸磁場與q軸磁場正交，這是直流電機數學模型及其控制系統比較簡單的根本原因。

交流電機是一個多變量、非線性、強耦合的系統，各物理量（電壓u、電流i、磁通Φ、電磁轉矩Te等）相互關聯，存在較強的耦合。例如，電磁轉矩正比于主磁通Φ和電流i，而Φ和i是隨時間變化的函數。因此，電磁轉矩的表達式中將出現兩個變量的乘積項，電機的數學模型復雜。采用坐標變換的目的就是將交流電機的物理模型等效為直流電機。

在理想條件下，當空間上三相互差120°的交流電機定子繞組中通以相位互差120°、頻率為ω的三相正弦交流電時，在空間上產生一個角速度為ω的旋轉磁場。同理，在空間上相互垂直的兩相繞組（α，β）中通入相位互差90°、頻率為ω的兩相平衡交流電流，也能建立同樣的角速度為ω的旋轉磁場。在兩個相互垂直的靜止繞組d和q中分別通入直流電流產生的合成磁動勢也是靜止的。如果讓兩個繞組以一定速度旋轉，則原來靜止的合成磁動勢變為旋轉磁動勢。通過控制直流電流大小和旋轉速度，可保證該旋轉磁動勢與交流電流形成的旋轉磁動勢等效，即該套直流繞組與前述的交流繞組等效。從靜止側看，d和q繞組是與三相或兩相交流繞組等效的旋轉直流繞組；從旋轉側（d和q繞組）看，它們是相互垂直的靜止直流繞組［24］。

為了表達不同繞組之間的關系，坐標變換方法應運而生，即利用不同的坐標系用數學語言表達繞組間的等效關系。從數學角度出發，上述過程分作兩步執行更好理解：將三相靜止交流繞組等效為兩相靜止交流繞組，再等效為兩相旋轉直流繞組，即從ABC坐標系變換到αβ0坐標系再變換到dq0坐標系。經過上述坐標變換，交流電機具有了直流電機的特點，交流電機的數學模型大為簡化。

2.2 三相靜止到兩相靜止坐標變換

在電機分析中，常用的Clarke變換與最初的αβ0分量法在物理意義上不盡相同，但在數學意義上相似。在兩相靜止坐標系中，坐標軸可以定義為x，y或者m，n。但是，該變換由Clarke提出，并由αβ0分量法推廣而來，故坐標軸的定義保持不變，仍采用α，β變量描述。三相靜止坐標系和兩相靜止坐標系間的關系如圖1所示。

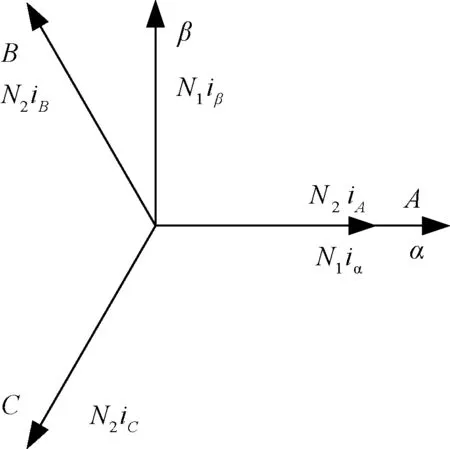
圖1 ABC／αβ0坐標變換示意圖

根據變換前后物理量之間的關系，Clarke變換包括等幅值變換和等功率變換。

2.2.1 等幅值變換

電機矢量控制中常用的是等幅值變換。根據變換前后旋轉磁場等效的原則，等幅值變換需維持綜合矢量（電流、電壓等）的幅值不變。

假設復平面上任意矢量x可以用ABC坐標系（α軸為復平面實軸，且與xa方向重合；β軸為復平面虛軸）下互差120°的分量xa，xb，xc表示。定義：

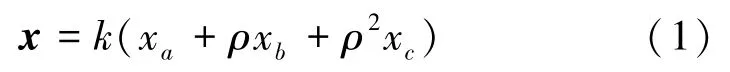
根據式（1）將x寫成復平面表達式，即：

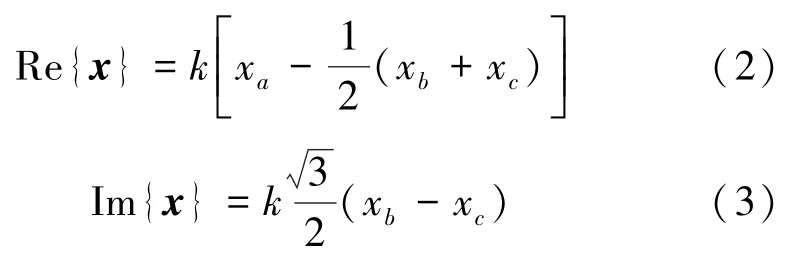
為分析方便，引入變量x0，定義：

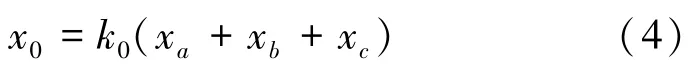
由式（4）可得：

將式（5）代入到式（2）中可得：

等幅值變換時，規定：

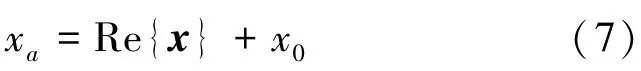
將式（7）代入到式（6）可得：

根據待定系數法，由式（8）可解得：

將解得的k，k0值代入式（2）、式（3）可得等幅值的變換形式：

將式（9）寫為矩陣形式：

式中：Cclarke為等幅值的Clarke變換矩陣。

2.2.2 等功率變換

區別于等幅值變換，在使用等功率變換矩陣時需注意保持變換前后系統的功率不變［25］。

如圖1所示，結合上述原則，有：

式中：iα和iβ表示αβ坐標系下的兩相電流；iA，iB和iC表示ABC坐標系下的三相電流；N1和N2分別表示兩相和三相繞組的有效匝數。

式（11）經整理后，用矩陣表示：

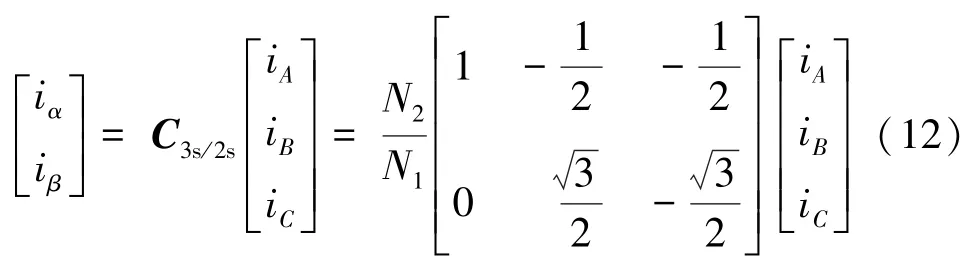
變換矩陣C3s／2s不是方陣，不能求逆，需引入一個獨立于iα，iβ的新變量i0，稱為零軸。零軸同時正交于α軸和β軸，構成三維空間的αβ0坐標系。

定義：

式中：k為待定系數。

引入新的變量后，式（12）可改寫：

將兩相靜止坐標系下的電壓u和電流i變換到三相靜止坐標系下的電壓u′和電流i′，因此有：

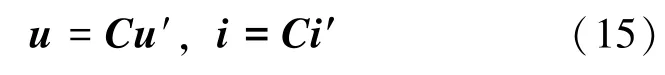
為實現可逆變換，C－1為矩陣C的逆矩陣，所以：

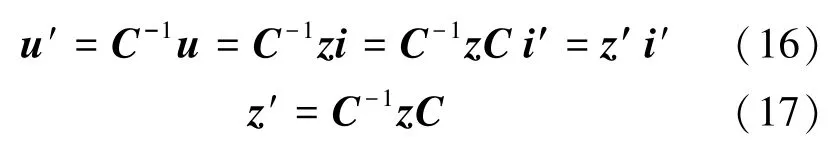
式中：z，z′為不同坐標系下的阻抗矩陣；u，u′，i，i′為不同坐標系下電壓和電流的行向量和列向量。

為滿足功率不變原則，在一個坐標系下的電功率應等于另一坐標系下的電功率，即：

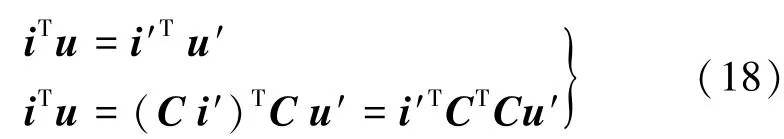
式中：CT為C的轉置矩陣；iT為i的轉置矩陣；i′T為i′的轉置矩陣。

為使式（18）成立，必須有

式中：I為單位矩陣。

因此，根據式（19），在功率不變原則的基礎上，變換矩陣C應該是一個正交矩陣。

定義矩陣C及其轉置矩陣CT：

將C及CT代入式（19），則有：

根據式（20），可分別求得：

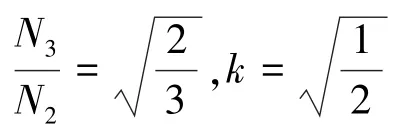
根據解得的值可求得C和C－1：

“我國的天主教、基督教一方面是宗教問題，另一方面，在長時期中又被帝國主義利用為對我國進行文化侵略的工具，其中一部分組織又被帝國主義利用為進行間諜活動的機關。這兩個宗教在我國都辦有教堂、學校、醫院及其他文化事業及救濟事業機關，都受外國津貼，都有大量外國傳教士占據領導地位。”⑧針對這一情況，河南展開了一系列全面清理帝國主義在宗教領域的影響的工作。

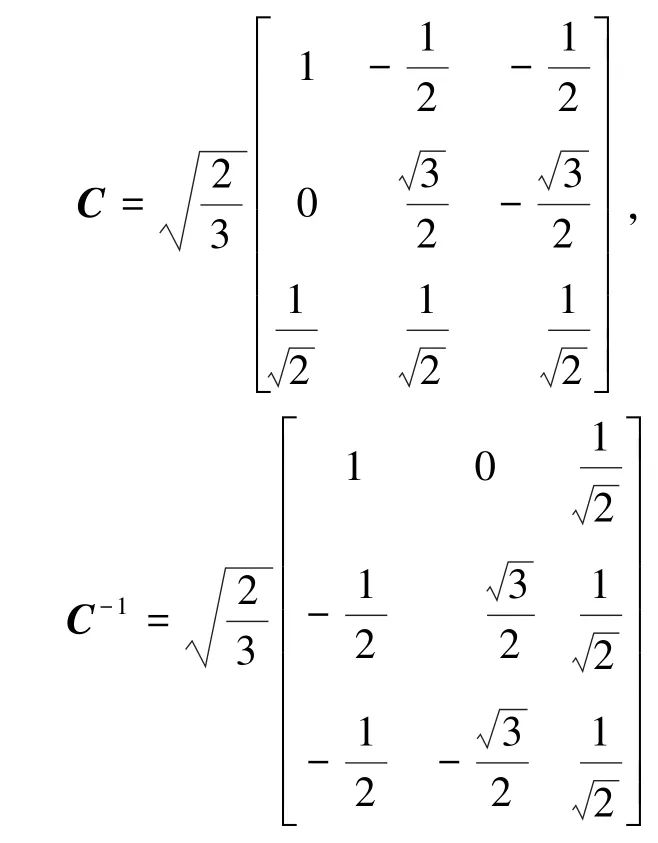
因此，等功率的變換式：

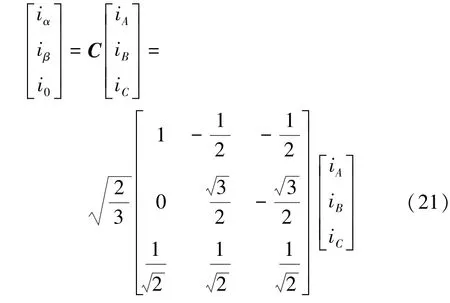
等功率的逆變換式：

上述三相靜止坐標系到兩相靜止坐標系的變換與Clarke當初為了進行不對稱分析而采用的αβ0分量法的性質不同，目的不同。但是，Clarke變換與αβ0分量法具有相似性，都實現了三相物理量到兩相物理量的轉換，因此人們將上述過程稱之為Clarke變換。筆者認為電機分析中的Clarke變換是一種廣義的變換，與最原始的αβ0分量法在本意上存在一定區別。

2.3 兩相靜止到兩相旋轉坐標變換

在Clarke變換所定義的αβ0坐標系中，一般規定α軸超前β軸90°，且α軸與A相繞組軸線方向重合。但對于Park變換，不同文獻給出了不同的dq0坐標系的定義。目前，主要有三種不同的dq0軸定義方式，具體如圖2所示。圖2（a）中，d軸超前q軸90°，規定d軸與A軸間的夾角為α；圖2（b）中，q軸超前d軸90°，規定d軸超前于A軸的夾角為α；圖2（c）中，q軸超前d軸90°，規定d軸滯后于A軸的夾角為θ。

圖2 不同dq0軸定義的坐標系統示意圖

不同的坐標軸定義，從ABC到dq0坐標系的變換矩陣不同，即對應上述三種情況的變換矩陣不同。下面對圖2（a）進行詳細分析。為便于理解，由靜止的αβ0坐標系變到dq0旋轉坐標系的變換稱為2s／2r變換。

由圖2（a）可得：

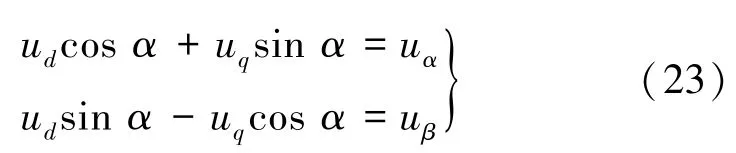
將式（23）改寫為矩陣形式：

對式（23）進行變換可得：

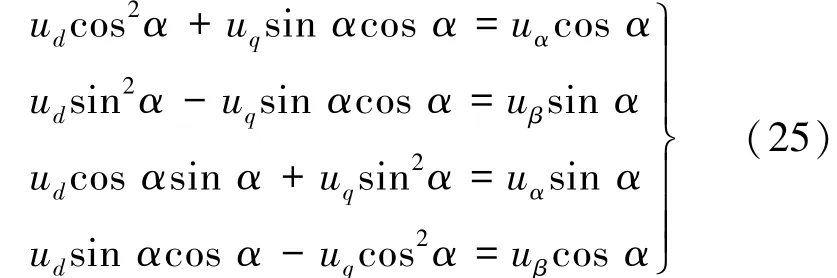
將式（26）改寫為矩陣形式：

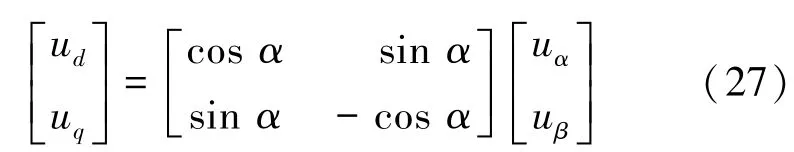
將式（27）與Clarke等幅值變換矩陣相乘，可得ABC／dq0變換的等幅值變換矩陣T3s／2r：

將式（27）與Clarke等功率變換矩陣相乘，可得ABC／dq0變換的等功率變換矩陣T3s／2r：

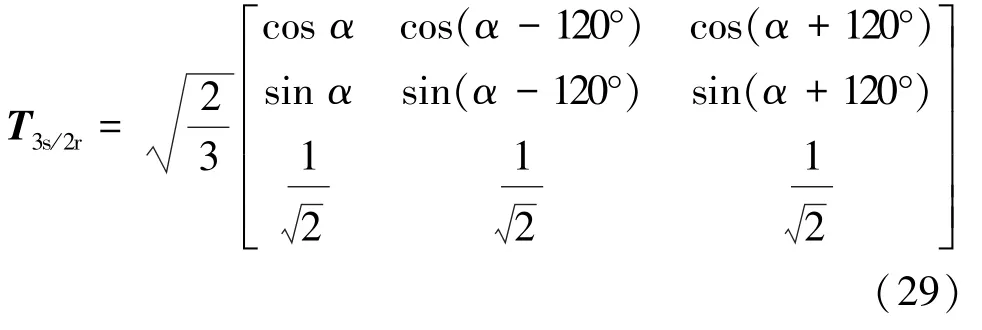
式（28）和式（29）分別為等幅值和等功率的ABC／dq0變換矩陣。

與圖2（a）相比，圖2（b）和圖2（c）中對dq軸的定義不同，所對應的2s／2r變換矩陣也不同，因此最終的ABC／dq0變換矩陣有所差別。

對于圖2（b），對應的2s／2r變換矩陣：

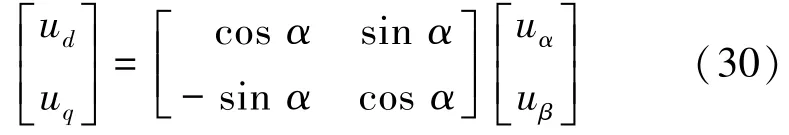
將式（30）與Clarke等幅值變換矩陣相乘，可得ABC／dq0變換的等幅值變換矩陣T3s／2r：

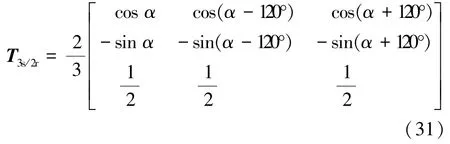
對于圖2（c），對應的2s／2r變換矩陣：

將式（32）與Clarke等幅值變換矩陣相乘，可得ABC／dq0變換的等幅值變換矩陣T3s／2r：

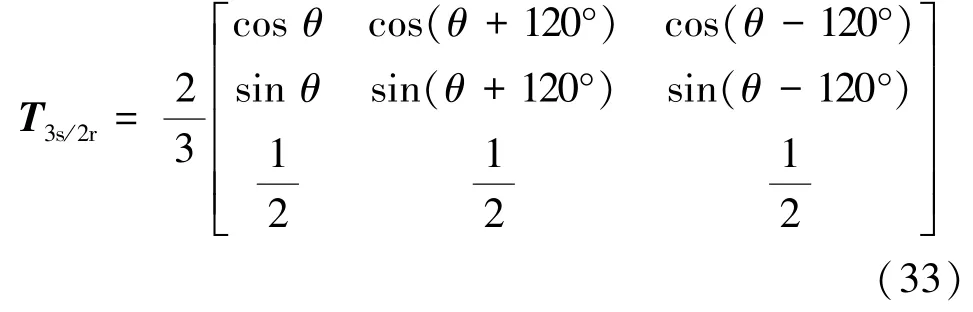
在等功率變換時，圖2（b）和圖2（c）的情況讀者可以自行推導，本文不再贅述。

上述兩相靜止坐標系到兩相旋轉坐標系的變換與當初Park為了分析凸極電機電樞反應而采用的dq0坐標變換的最終目的相同。但是，原始的Park變換是指從ABC到dq0的坐標變換，而目前大部分文獻所指的Park變換專指從αβ0到dq0的坐標變換。由此，筆者認為目前的Park變換是一種“狹義”的Park變換，僅是原始Park變換的一部分。

3 坐標變換的誤用及混淆

3.1 誤用實例

由于文獻編輯工作失誤、排版印刷錯誤、參考引用過程漏洞等原因，部分文獻、資料及書籍在介紹、使用Clarke變換和Park變換時出現偏差，致使三相對稱交流量到兩相直流量的變換失敗，最終誤導工程技術人員、延緩工程項目開發以及延誤科研項目攻關。

文獻［26］中（1.2.1 Clarke變換與仿真）提到：

與式（10）和式（21）相比，式（34）表示的Clarke變換矩陣既不是等幅值變換，也不是等功率變換。

該書中后文（1.2.2 Park變換與仿真建模）提到：

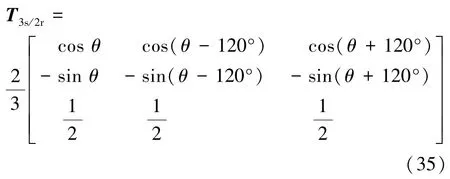
根據式（35），我們推斷式（34）應是等幅值的Clarke變換。因此，根據本文前面給出的定義，式（34）最后一行系數應為另外，文獻［16］也存在該問題。

當建立被控對象在dq0坐標系下的數學模型時，文獻［9］在進行坐標變換時沒有給出相應的假設（前提）條件，對αβ坐標軸的定義有誤，并且混淆了等功率和等幅值的變換，推導過程不連貫。文獻［10］未給出dq坐標軸的定義。文獻［13］將id作為iq進行控制，混淆了dq軸的基本概念。文獻［17］描述的dq坐標系與dq軸的實際定義不相符。上述情況出現較多，本文不再贅述。

3.2 定義混淆

目前，不同文獻對Park變換的定義存在一定分歧。諸多電機及其控制的相關文獻、書籍等將Clarke變換定義為ABC／αβ0變換，將Park變換定義為αβ0／dq0變換［8?16，26］。但是，文獻［27］中將Park變換定義為ABC／dq0變換，具體變換矩陣：

同樣的，文獻［17］也提到：“交流電機理論所研究的內容主要是處于相對運動狀態的電路行為問題，由于電機中布置有許多在磁路上耦合又處于相對運動中的電路，分析工作顯得十分復雜，甚至難以進行。1929年，Park針對凸極同步電機轉子不對稱的特點，提出了著名的Park方程。這是一個將實際存在的三相靜止電路中的電壓、電流等變量變換到與之等效的旋轉dq軸參考坐標系內相應量的坐標變換公式。”

回顧Park于1929年發表的文章，該文章在雙反應理論基礎上推導出ABC／dq0變換，并未經過αβ0坐標系統的轉換，式（37）是最初Park提出的變換方程。

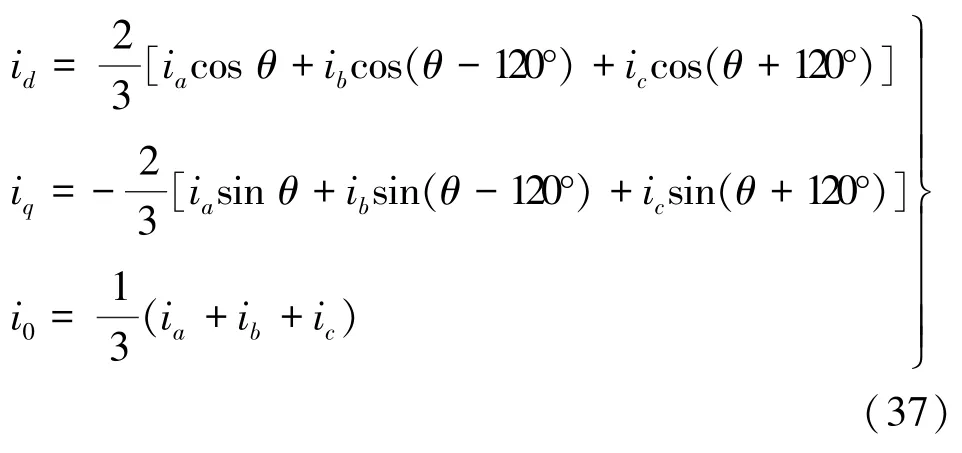
值得注意的是，Clarke首次提出αβ0坐標系大約是在20世紀30年代末期，因此，無論是從時間上來看，還是從推導原理與過程上來看，Park變換所指的應當是ABC／dq0變換，與αβ0并沒有直接關系。若將αβ0坐標系作為Park變換（3s／2r）的中間環節，即我們所熟知的3s／2s／2 r變換，可使抽象的坐標變換更容易理解，在一定程度上簡化推導過程。雖然這種經αβ0坐標系過渡的坐標變換推導方法已在教學和科研中廣泛采用，但原則上Park變換本質是由ABC三相靜止坐標系變換到dq0旋轉坐標系這一點不可混淆，且有必要澄清。在教學與科研過程中，部分文獻忽略了Park變換與Clarke變換的歷史演變過程，混淆了兩種坐標變換間的先后關系，導致目前Park變換定義混亂。

雖然，目前所應用的Clarke變換和Park變換與它們的原始定義存在偏差，但為了避免引起混亂，便于閱讀和理解，本文在后續討論中暫且采用Clarke變換和Park變換分別描述ABC／αβ0變換和αβ0／dq0變換。

4 仿真分析及驗證

4.1 基本坐標變換的仿真分析

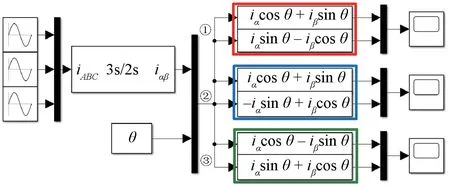
圖3 坐標變換仿真模型

圖3為在Simulink軟件中搭建的等幅值Clarke變換和不同dq0坐標系下的Park變換仿真模型，用于對比坐標變換的不同結果。

仿真模型的輸入信號為三相對稱的幅值均為1的正弦電流信號，頻率為50 Hz。圖3中，3s／2s模塊即為等幅值的Clarke變換，①、②、③三個模塊分別對應圖2（a）、圖2（b）、圖2（c）中三種不同dq0坐標系下的2s／2r變換。

Clarke變換的結果如圖4所示。α軸分量超前于β軸90°，且變換前后變量的幅值相等，均為1。

圖4 Clarke變換仿真結果

圖2（a），圖2（b）和圖2（c）三種坐標系下Park變換的結果分別如圖5（a），圖5（b）和圖5（c）所示。

圖5 Park變換仿真結果

由于坐標軸定義不同，在圖5（a）和圖5（b）中變換后的dq軸分量顛倒，或體現為dq軸超前和滯后的變化。在圖5（c）中，Park變換未能將三相對稱的正弦量變換為兩相直流量，分析圖2（c）的dq0坐標系，其定義的角度θ為d軸滯后于α軸的角度，相較于圖2（b）所定義的角度α，兩者之間關系滿足θ＝－α。由于仿真模型中采用的角度為α，因此修改仿真模型，將α乘以－1以符合對θ的定義，結果如圖5（d）所示。

上述仿真分析揭示了不同dq0坐標系定義對應的坐標變換結果差別，給出了輸出錯誤的具體形式。相關科研人員可以借鑒該結果，指導各自的仿真分析工作。

4.2 錯誤使用變換矩陣的影響

MATLAB／Simulink軟件庫中含有封裝好的坐標變換模塊，該模塊默認的坐標系定義與圖2（b）一致。建立電機數學模型時，若采用圖2（b）的dq0坐標系，則仿真時可直接調用坐標變換模塊。但是，若所建立的數學模型與仿真模型采用的坐標系不一致，則無法得到預期的結果。例如，若建立電機數學模型時選用圖2（c）的dq0坐標系，而仿真時直接調用Simulink庫中的坐標變換模塊，會導致錯誤出現。此時所得dq軸分量不是直流量，無法達到預期效果，系統不穩定。

以永磁同步電動機調速控制系統為例，采用id＝0的控制策略開展仿真分析。將三相電流變換為旋轉的兩相直流量，分別對id和iq進行控制。

1）采用圖2（b）的q軸超前d軸（常用）坐標系，即Simulink中坐標變換模塊默認的定義，仿真結果如圖6所示。永磁同步電動機能夠正常運行，在準確跟蹤給定轉速的同時，若負載突變，轉速仍可以維持穩定且波動較小，控制性能較好。

圖6 Park變換中q軸超前d軸時的仿真結果

2）采用圖2（a）中的d軸超前q軸的坐標系，仿真結果如圖7所示。假設建立的數學模型與仿真模型采用的坐標系不一致，即Park變換矩陣不同，此時若不對仿真模型加以調試、改動，整個系統不能按照預期的控制效果正常運行。經分析，該坐標系與前述q軸超前d軸坐標系的區別在于兩者q軸的方向相反（相差180°）。因此，在模型中將q軸電流乘以－1再進行控制，電機可以穩定運行且控制性能較好。具體仿真結果如圖7所示，與圖6所示類似，此處不再贅述。

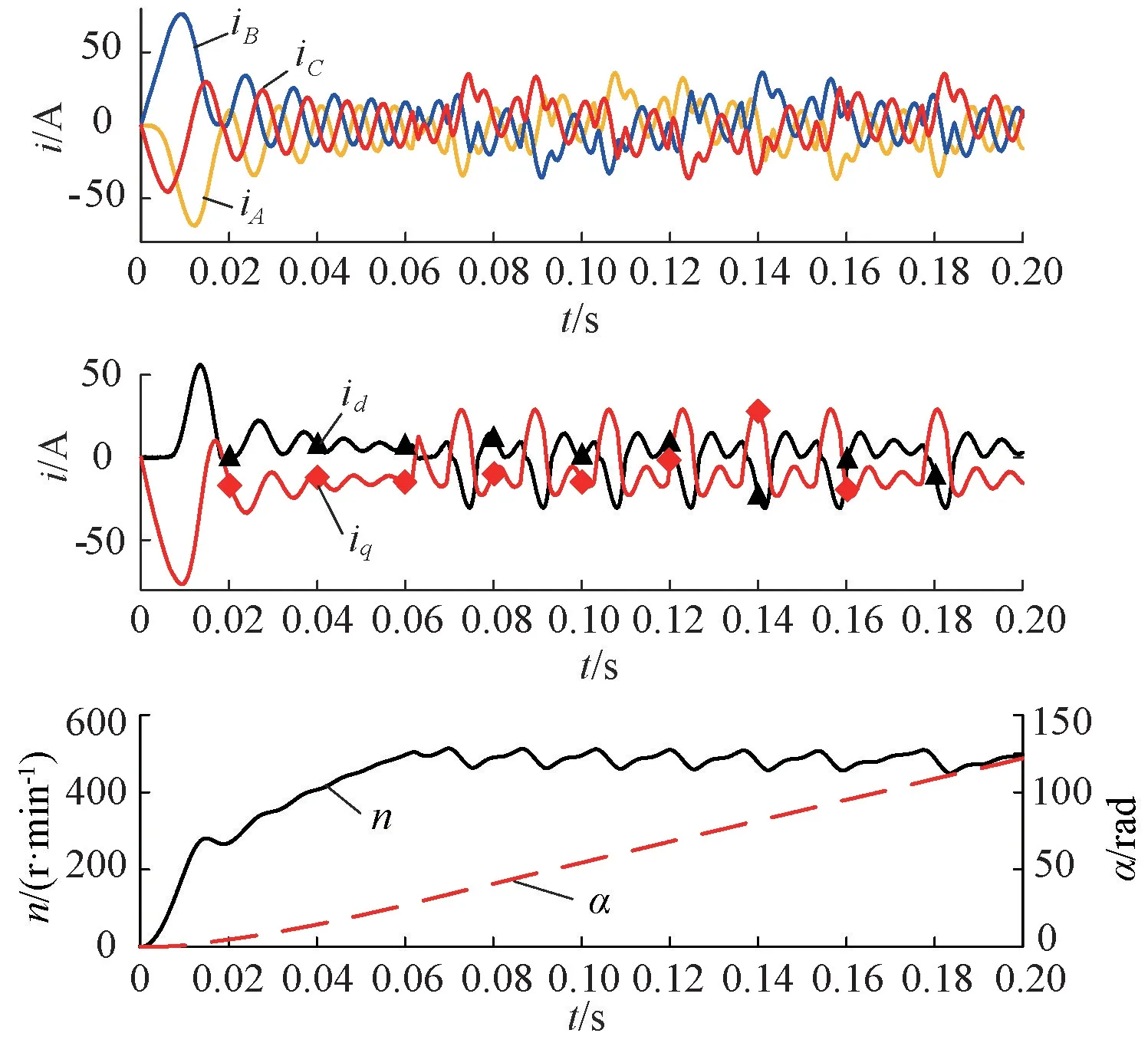
圖7 Park變換中d軸超前q軸時的仿真結果

3）采用圖2（c）中的q軸超前d軸的坐標系，對角度的定義與圖2（b）不同，仿真結果如圖8所示。

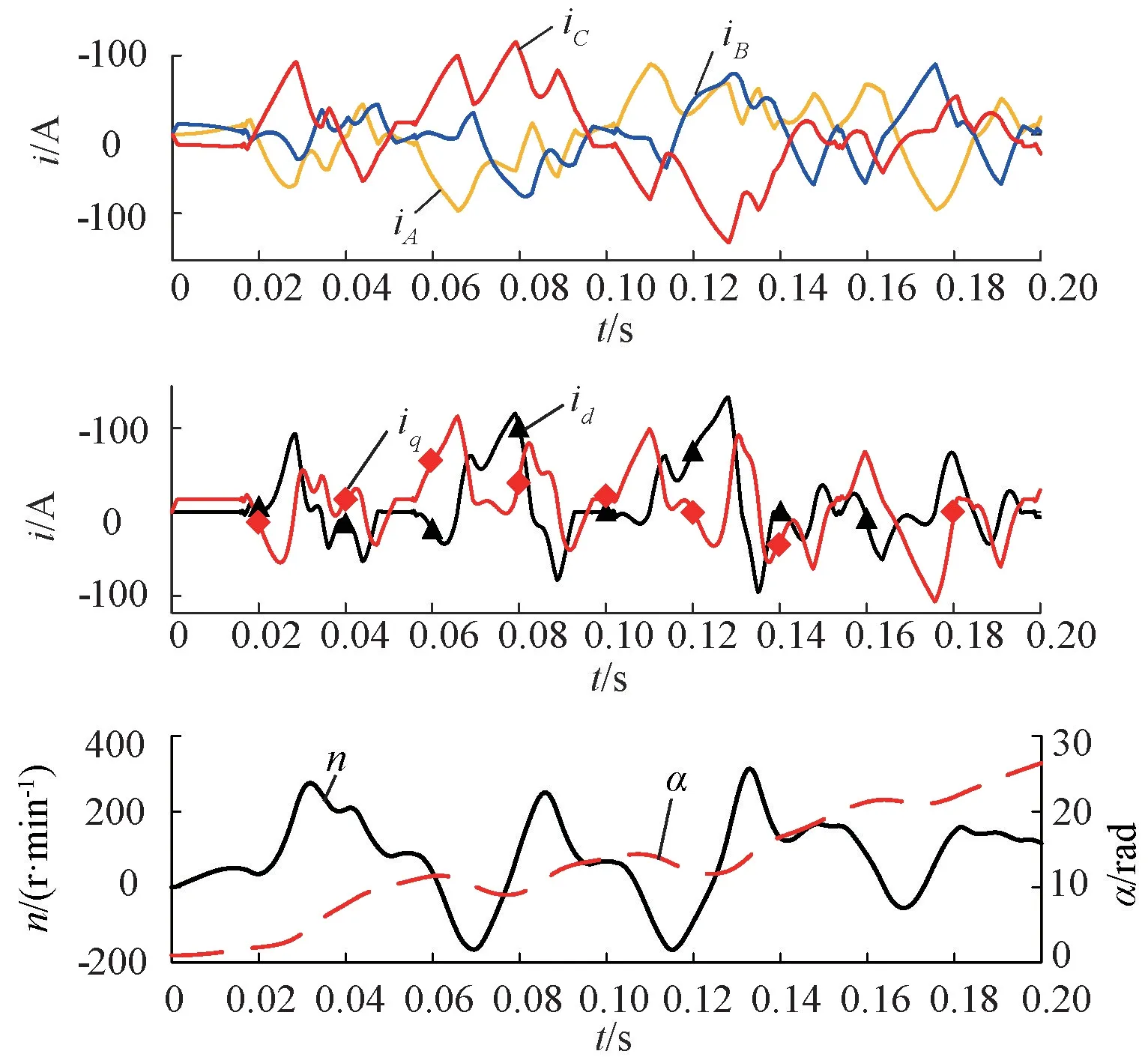
圖8 Park變換中q軸超前α軸時的仿真結果

若不對模型進行調試，此時系統不穩定，無法按照預期正常運行。根據前述分析，該坐標系定義的角度θ為d軸與α軸之間的夾角，與仿真模型實際采用的角度α之間滿足θ＝－α。因此，修改模型中對應的電角度，將其乘以－1再進行變換，電機正常運行。

對比上述三種情況可以發現，當dq軸的選取與模型中坐標變換矩陣不一致時，整個控制系統出現紊亂，無法達到預期的調速效果，甚至系統無法正常運行。

4.3 總結與分析

根據理論與仿真分析結果，使用Clarke變換與Park變換時需注意：

1）采用坐標變換時，需假設三相繞組空間相差120°，且繞組內的各物理量幅值相等，相位互差120°，若實際不滿足上述假設條件，變換后的參數無法解耦；

2）選定等幅值或等功率變換后，應保證數學建模和仿真分析采用的變換矩陣一致，不可隨意更改；

3）區分αβ軸和dq軸的超前滯后關系，不應混淆：αβ0坐標系為靜止坐標系，對αβ分量的超前滯后判斷應參考各自的時間相位；dq0坐標系為旋轉坐標系，對dq分量的超前滯后判斷應參考各自的空間位置；

4）旋轉角α（或θ）定義為d軸與α軸的夾角，仿真分析與數學建模所采用的角度應保持一致。

目前Park變換中初始定義的q軸超前d軸的坐標系已被廣泛使用，并且Simulink中默認的坐標變換模塊也采用了該定義，仿真時直接調用該模塊或簡單調試后基本可以保證系統正常運行。在實際仿真過程中，遇到上述系統不穩定的情況并不常見。但脫離仿真軟件，獨立建立電機數學模型時，部分學者、學生及工程技術人員并不注意坐標系的定義和采用坐標變換的前提條件等問題，直接套用變換矩陣。實際上，數學建模采用的坐標系與仿真建模采用的坐標系可能不一致，故人為地將數學建模與仿真建模割裂開，這也是目前高度依賴仿真軟件而忽視理論分析的體現。此外，若實際上應用坐標變換的條件并不滿足而仍采用坐標變換進行分析，那么所得結論也是不可靠的。出現上述情況后，雖然仿真系統經過調試能夠正常運行，但對坐標變換定義不清晰、理解不深刻、用法不恰當等問題沒有明顯體現出來，因此造成無法真正掌握、靈活運用Clarke變換與Park變換等問題。

5 結 語

本文梳理了Clarke變換和Park變換的發展歷程，分析了對坐標變換定義混淆和由于闡述不嚴謹導致的變換矩陣誤用等問題，通過永磁同步電動機調速系統仿真展示了變換矩陣的誤用后果。通過本文不同角度的分析，希望學生、學者和工程技術人員加深對坐標變換的理解，激發對基本理論的探索，樹立嚴謹求實的態度，合理、準確地應用坐標變換方法。