基于特征頻率篩選的聲發射信號去噪算法

陳文峰， 向華， 許光達， 柯西江

（1.華中科技大學 機械科學與工程學院，武漢430070; 2. 國家數控系統工程技術研究中心，武漢430070）

0 引言

刀具的狀態與加工的質量一直是機床領域的關注的焦點，而聲發射（Acoustic emission，AE）技術作為對應力作用狀態監測的一種手段，在刀具磨損監測和加工質量監控領域發揮著重要的作用。AE本質是材料應變能以彈性波的形式釋放[1-3]，所以大應力作用下的去除成形將產生大量的AE事件[3]。同樣的，機械傳動的過程是應力在多個對象間的傳遞，也會產生一定的AE事件。所以在復雜加工環境中，采集的原始AE信號（以下簡稱原始AE信號）包含了非加工產生的AE信號（以下簡稱非加工信號）與加工產生的AE信號（以下簡稱加工信號）。為獲得清晰的加工信號，需對原始信號進行去噪。

非加工信號源有：機床自身、機床內部的液壓與氣壓系統、機械運動過程的撞擊及所有摩擦過程[4]。非加工信號主要由加工外的應力作用產生，非加工信號與加工信號的性質相似，在頻域上均分布在100 kHz～1 MHz[5]。但非加工信號源的位置與傳感器間存在多種不同的介質，傳感器采集的信號實際已在各類介質中發生多次界面反射、干涉與衰減，且屬于介質模態頻率分量的信號會被增強，最終在100 kHz～1 MHz的頻譜中表現為散布的多個高能峰，進一步可以將這類頻率概括為一種離散的頻率分布，并將這些頻率視為該分布的特征頻率，而加工信號在頻域具有為低幅值、寬頻帶的特點，進一步可以概括為一種連續頻率分布[6-7]，如圖1所示。

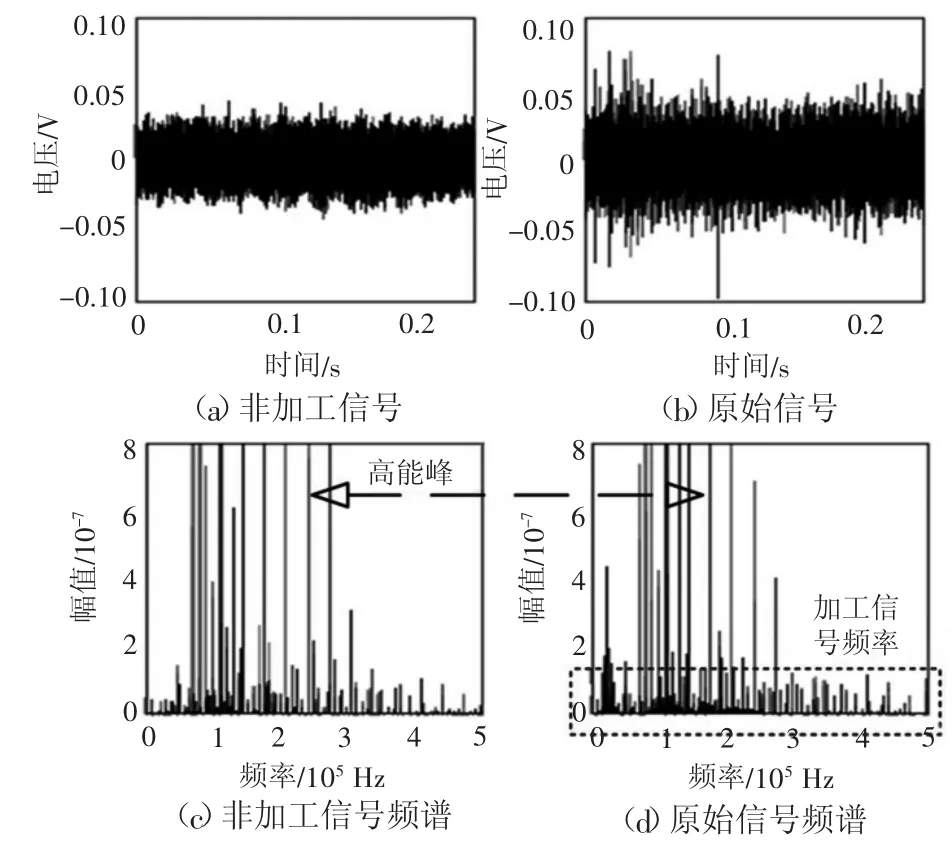
圖1 離散頻率分布與加工信號頻率示意圖

早期受限于計算機性能，對原始信號中加工信息的提取以RMS濾波、振鈴計數等硬件手段為主[1,7]，無法處理非加工信號的干擾。近幾年，隨著計算機的處理性能的發展，在加工領域中，聲發射分析技術逐漸從參數法分析法轉向頻域與時頻域分析[3,8-9]。對非加工信號也逐漸在頻域與時頻域進行研究，X.Chiementin等[10]對于軸承的AE信號，分別對自適應濾波方法（Self-Adaptive Cancellation，SANC）、譜減法與小波降噪方法進行實驗與分析，得出自適應濾波方法降噪效果最佳的結論。王宗煉等[11]、程鐵煉等[12]、王雨虹等[13]、李占國等[14]均采用小波包降噪的方法對原始信號進行去噪。而王麗華等[15]則基于自動編碼器無監督網絡去除非加工信號。上述對非加工信號處理算法的研究，取得了一定的進展與效果，但均停留在實驗室階段，加工環境理想、信號清晰，并且未結合非加工信號離散頻率分布的特點，在面對復雜的實際加工環境時，對原始信號的去噪效果十分有限。但結合離散頻率分布特點，使用通用的帶阻濾波方式，由于加工信號寬頻帶的特點，將損失阻帶邊沿加工信號的頻率分量。

對此，本文根據非加工信號離散頻率分布的特點，提出基于特征頻率篩選的去噪算法——DCFS。并與自適應濾波算法與帶阻濾波算法進行去噪效果比較，DCFS具有最優的去噪性能。本文將在第1節中，介紹DCFS算法的原理與實現方法，第2節介紹實驗方法與實驗結果的分析與比較，第3節對非加工信號的特點及DCFS進行總結。

1 基于特征頻率篩選的去噪算法

將機床空運行時AE信號視為非加工信號，以便對非加工信號的特點進行直觀的觀察，實際機床的原始信號與非加工信號及其頻譜如圖1所示。根據圖1中（c）～（d）的頻譜分布關系，可以直觀地發現，非加工信號頻譜存在多個分散的高能峰，且在原始信號頻譜中依舊存在，而原始信號本身在低幅值處存在連續的頻率分布，該頻率分布只出現在加工過程中。對此可以得出，非加工信號是一種離散頻率分布的信號，并且該頻率分布在加工過程中依然存在，而加工信號在低幅值處具有較為連續的頻率分布。

DCFS算法結合上述離散頻率分布的特點，將離散分布的頻率視為非加工信號的特征頻率，以這些特征頻率的頻率大小與幅值為依據，對原始信號進行去噪，具體可概括為兩個子方法：基于去噪特征頻率窗口滑動的頻譜篩選方法、基于iFFT的去噪信號重構方法。算法的總的流程與效果如圖2所示。

圖2 DCFS流程與效果示意圖

1.1 基于去噪特征頻率窗口滑動的頻譜篩選方法

基于去噪特征頻率窗口滑動的頻譜篩選方法，可以分為兩個步驟：非加工信號特征頻率選取與原始信號特征頻率篩選與抑制。因為需要進行頻率選取，所以需通過快速傅里葉變換（FFT）獲得頻譜序列，FFT的核心離散傅里葉變換公式如下，并換算出幅值能量與相位：

其中：N為離散信號點數；Y（ω）為幅值能量；phase（v）為相位。

非加工信號特征頻率選取需結合離散分布的頻率的高能峰特點，為了確定頻率分布中高能頻率與低能頻率分界幅值，本步驟先對非加工信號進行FFT，得到幅值Y，并對其進行降序排列獲得Ydes與其差分Ydes′，保留Ydes和Ydes′與頻率值的映射關系，通過設定的閾值，確定幅值變化放緩的臨界點。視該臨界點為高低能分量的幅值分界點，根據映射關系確定高幅值的頻率集合Fpeak：

該步驟算法為提取特征頻率集合，

輸入為非加工信號x(n)，輸出為特征頻率集合Fpeak、特征頻率幅值Ypeak。具體流程為：1）開始；2）加載非加工信號x(n)；3）[F,Y]= FFT(x(n))←FFT獲得頻率與對應幅值；4）Ydes(n)=Y↓、Ydes′(n)=Ydes(n+1)- Ydes(n)←Y(n)降序排列并差分；5）Fpeak=[F|Ydes(F)＞1×10-9；|Ydes′(F)|＞1×10-11]，Ypeak=Y(Fpeak)←確定特征頻率；6）結束。

各階段操作流程與效果如圖3所示。

原始信號特征頻率篩選與抑制則根據已獲得特征頻率集合Fpeak中的各元素的頻率值，循環對原始信號頻譜對應的區域進行篩選。本步驟將以Fpeak的頻率值為中心，在原始信號頻譜中構建正負方向、長度可調的窗口。結合特征頻率幅值大、離散分布的特點，通過窗內的幅值分布情況，判斷該窗內是否存在近似的特征頻率。

圖3 非加工信號特征頻率選取示意圖

若不存在特征頻率，則不進行抑制；若存在近似特征頻率，則根據窗內非特征頻率的幅值分布關系，利用最小二乘（Least squares，LSQ）多項式擬合方法，確定抑制后特征頻率的幅值大小。最小二乘多項式擬合方法如公式（4）、公式（5）：

式中：多項式基函數選擇｛1，x，…，xm｝；xi為非特征頻率；yi為非特征頻率幅值；wi為權函數，本算法取1；φ（x）為擬合多項式函數，多項式系數｛a0，a1，…，am｝為方程（4）的解。

將特征頻率帶入φ（x）即獲得抑制后特征頻率處的幅值。經過循環，最終獲得去噪后的加工信號的頻率分布關系。輸入為原始信號xoriginal(n)、特征頻率集合Fpeak、特征頻率幅值Ypeak，輸出為加工信號頻率幅值Ymanu、相位Phase。具體算法流程為：1）開始；2）加載原始信號xoriginal(n)；3）F(ω) =FFT(xoriginal(n)) phase=arctan(Re(F)/IM(F))，Y=||F||←FFT獲得頻率與對應幅值和相位；4）i=1，N=size(Fpeak)；5）當i＜N；6）Yw=Y(Fpeak(i)±L)，Fw=Fpeak(i)±L←構建長度為2L的窗體；7）Ywdes=Y↓Ywdes′= Ywdes(n+1)-Ywdes(n)←降序排列窗內幅值；8）判斷窗內是否存在||Ywdes′||＞1×10-8，不存在開啟下一次循環←判斷是否存在離散分布的特征頻率；9）Fwpeak=[F| ||Yw(F)-Ypeak(Fpeak(i))||＜1×10-8] ←篩選窗內高能分量；10）Fwpeak是否為空，若空則至14；11）Fleave=[F|F∈Fwpeak(n)&&F∈Fw(i)]，Yleave=Y(Fleave)←確定窗內非特征頻率及幅值；12）=LSQ(x=Fleave，y=Yleave)←最小二乘擬合幅值分 布關系；13）Y(Fwpeak)=←確定特征頻率抑制后幅值大小；14）i=i+1；15）結束循環；16）Ymanu=Y←保留抑制后的加工信號頻率幅值；17）結束。

算法示意圖如圖4所示。

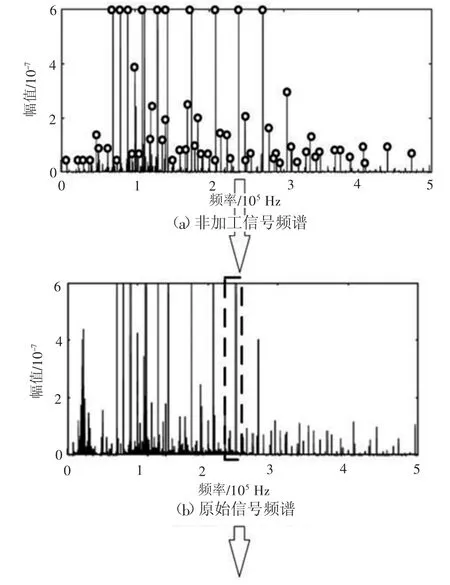
圖4 原始信號特征頻率篩選與抑制示意圖

1.2 基于iFFT的去噪信號重構方法

對于抑制后的頻譜圖結合原始信號的頻率相位信息，結合關系公式:

使用新構建的復信號進行快速傅里葉逆變換，獲得原始信號中的加工信號，該信號重構流程示意圖如圖5所示。

離散快速傅里葉變換公式為

圖5 信號重構示意圖

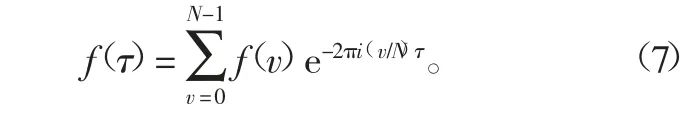
DCFS受常規譜減法的啟發設計而成，但是在該應用場景中，離散頻率分布的頻率幅值并不是固定的，常規譜減法無法處理頻率幅值存在一定波動的情況，同時無法保留被抑制頻率分量中加工信號的分量。對此結合離散頻率分布的特征頻率的特點，設計了上述的DCFS算法，在保留原始信號中加工信號分量的同時，有效抑制了非加工信號的分量。

2 DCFS實驗驗證

為了驗證DCFS的實際去噪效果，本實驗在實際工廠的加工環境下進行實驗，采集非加工狀態與加工狀態時的數據，對數據使用DCFS進行去噪，并與LMS-自適應濾波算法和帶阻濾波算法進行比較。

2.1 實驗設備與方案

本文采用的實驗設備與器件主要為：kistler 5125C聲發射信號調理儀，kistler 8152C聲發射傳感器，NI-9223電壓采集卡，白鋼與鎢鋼φ10直柄立銑刀，尺寸規格為15 mm×60 mm×160 mm的6063鋁合金、45鋼、7075鋁合金。

實驗在常溫下Z540B銑床上進行，對工件一側進行同方向循環面銑削，將回程空運行作為非加工信號。采集卡采樣頻率1MSPS，傳感器信號調理儀自帶50～500 kHz帶通濾波器。為貼近實際生產加工中聲發射傳感器的使用方式，將聲發射傳感器安裝在通用夾具一側。實驗裝置連接示意圖如圖6所示。為驗證算法的適用性，采集了不同刀具及不同材料情況下的加工與非加工信號。具體實驗方案如表1所示，共計180組數據。

2.2 實驗結果

圖6 實驗設備連接拓撲圖

表1 實驗參數

對采集數據使用DCFS對數據進行去噪，對比180組數據的結果，去噪算法生成的加工信號保留了原始信號中加工分量的聲發射信息，非加工聲發射信號被抑制。部分實驗結果如圖7～圖9所示。

2.3 算法比較分析

為了與其他算法進行比較，需設定一個可量化指標對去噪效果打分，但實際情況中無法獲知原始信號中的真實加工信號或者真實的非加工信號，不能采用常規的功率類評價指標，如信噪比（SNR）、均方根差（RMSE）。對此本文采用歸一化互相關函數最大值（以下簡稱互相關值）作為兩信號關聯程度的判定。互相關函數峰值采用如下公式：

圖7 各參數第一組1刀去噪前后數據對比圖

其中：x，y為輸入信號；N為信號長度；R^xx（0）和R^yy（0）分別為x與y的自相關函數值。式（9）中的最大互相關值表示兩信號相關性，若關聯性越大，則值越大。使用加工信號與原始信號的互相值及加工信號與非加工信號的相關值值作為去噪效果的評判依據，要求前者保持一個較高的值，而后者應為低的值。

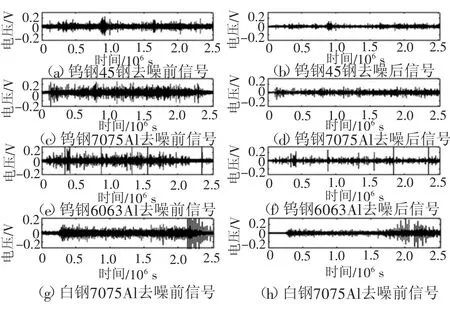
圖8 各參數第二組8刀去噪前后數據對比圖

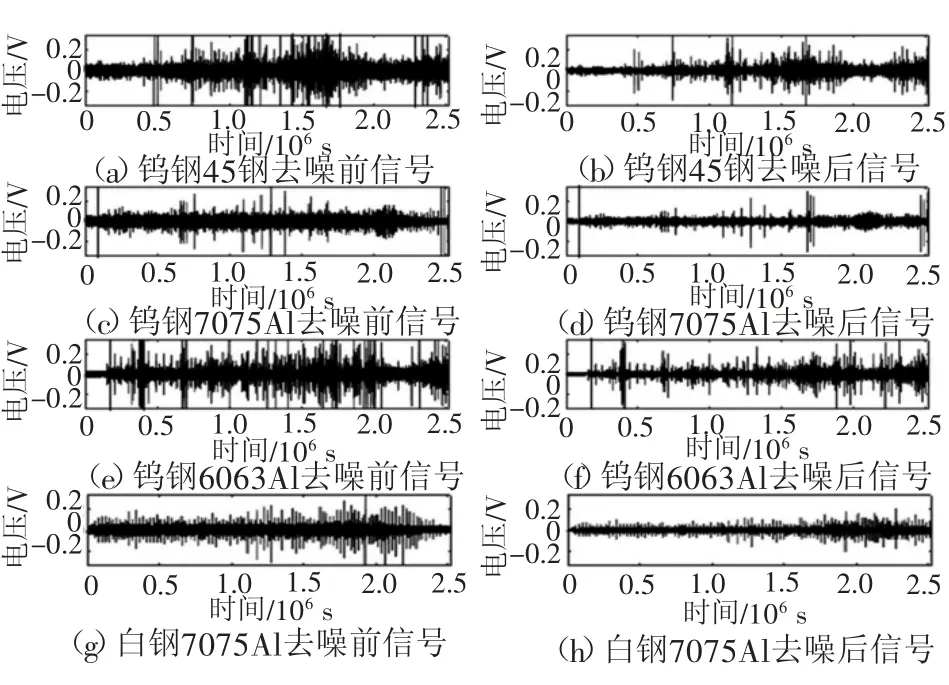
圖9 各參數第三組15刀去噪前后數據對比圖

為比較DCFS的去噪效果，對所有數據分別使用LMS-自適應濾波、DCFS、帶阻濾波。對結果進行相關性分析，以加工信號與非加工信號相關值作為橫坐標，以加工信號與原始信號相關值作為縱坐標，構建二維結果分布圖，最終結果如圖10所示。根據相關值的評價指標要求可得出，圖中越位于右下角則去噪效果越好，越位于左上角則去噪效果越差。

根據圖10所示，DCFS相比于LMS-自適應濾波算法與帶阻濾波算法，180組數據均處在圖像右下角，針對不同刀具與不同材料均表現出了良好的去噪效果，在3種算法中去噪能力最佳。帶阻濾波結果集中在圖像左上角，去噪效果在三者中最差，驗證了前文對于帶阻濾波去噪過程中損失阻帶邊沿加工信號能量的論述。LMS-自適應濾波則與原始信號存在著極高的相關性，與非加工信號也存在較高的相關性，去噪能力有限。

3 結語

本文將實際機床采集的聲發射信號作為研究對象，以頻譜分析為工具，對機床中非加工聲發射信號的特點進行了分析，發現該信號是一種離散頻率分布的信號，并提出了一種有效的去噪方法，具體得出了以下兩點結論：

1）經實驗數據驗證，提出銑削機床中加工聲發射信號的非加工分量在頻域中呈現散布的多個高能峰，具有一種離散的頻率分布的特點，且在機床運行過程中持續存在。本文視高能峰為特征頻率，在采集的180組數據中，特征頻率值始終保持在相同頻率上。這些特征頻率為進一步進行去噪算法的設計與銑削加工狀態分析提供基礎。

2）結合非加工信號的離散頻率分布的特點，設計了基于特征頻率篩選的去 噪 算法——DCFS。該方法在保留銑削中加工聲發射信號分量的前提下，有效抑制了非加工信 號。 經180組數據測試，去噪效果穩定，且優于通用的帶阻濾波方法與LMS-自適應濾波方法。該算法能有效適應嘈雜的加工環境，提升了聲發射技術在復雜工廠應用的可能性，為進一步開發刀具狀態監測與加工質量監控提供了清晰的信號。

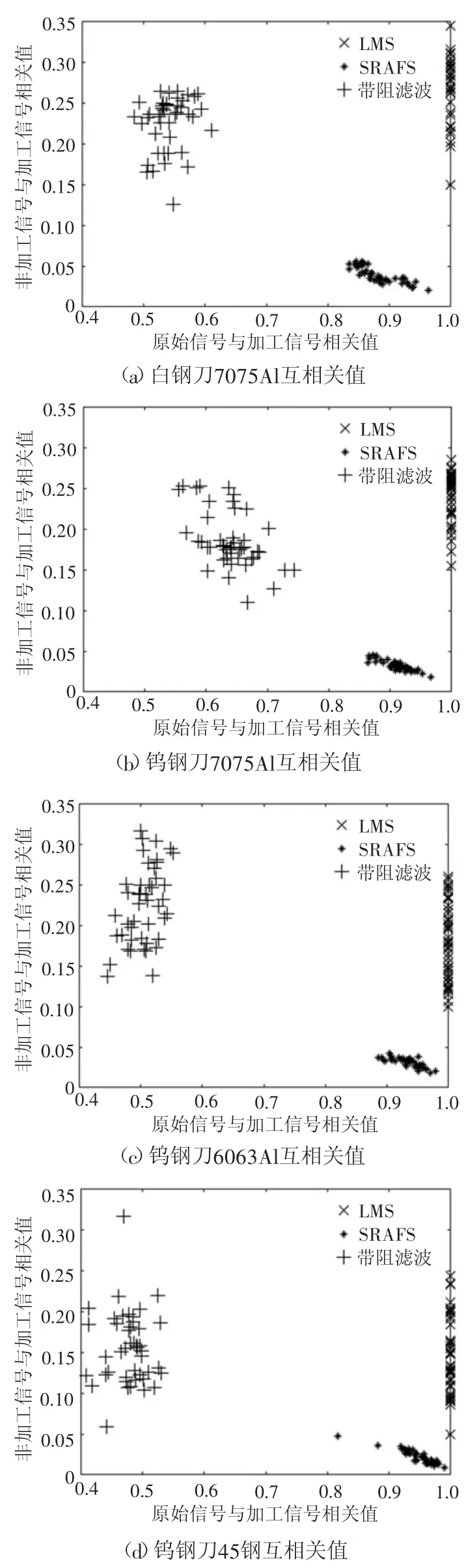
圖10 各數據非加工信號-加工信號/原始信號-加工信號相關值分布圖